Pricing a European Option in a Black-Scholes Quanto Market When Stock Price is a Semimartingale ()
1. Introduction
This paper considers the European call option in the Black-Scholes market when the exchange-rate is a semimar- tingale. Specifically, we consider a problem of a Dollar investor seeking to invest in a Sterling market. Theory of exchange rates has been widely discussed (see [1] -[4] ). Exchange rates change with time due to a number of factors, such as changes in fiscal and monetary policies, interest rate differentials between two countries usually resulting in revaluation or devaluation of currency. The main challenge is to construct a model which captures the dynamics of exchange rate and its effect when investments are made in different currencies. A number of models have been developed which are being modified to accommodate reality. Generally, exchange rate models fall into two major categories: Those that treat the dynamics of exchange rate as a continuous process and those treat exchange rates as processes with jumps. The Black-Scholes model is the most celebrated non- jump model whose dynamics are modelled by the stochastic differential equation 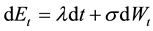 where
where 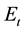 is the exchange rate, λ is the drift parameter, σ is the volatility parameter and Wt is a Wiener process. This model assumes the logarithmic exchange which follows Brownian motion with drift. Using this as a benchmark model,
is the exchange rate, λ is the drift parameter, σ is the volatility parameter and Wt is a Wiener process. This model assumes the logarithmic exchange which follows Brownian motion with drift. Using this as a benchmark model,
other models were developed, for example, a model given by the equation 
where  is a pair of correlated Brownian motions with correlation co-efficient ρ and
is a pair of correlated Brownian motions with correlation co-efficient ρ and
 is Brownian Motion driving the given asset prices [2] . It is known that jump-diffusion models are more realistic for studying the dynamics of exchange rates [3] . Dating back from the introduction of jump-diffusion process by [4] [5] as a tool for modelling the prices of options based on more general processes of underlying asset returns, jump-diffusion processes have also been widely used in modelling the dynamics of exchange rates. Empirical evidence based on simple jump-diffusion models suggests that jumps really form significant com- ponents of foreign exchange rate processes [1] [3] . As such, it is reasonable that both empirical and theoretical studies of exchange rates under uncertainty should allow for the presence of discontinuities explicitly. There has been a wide use of jump-diffusion processes to model financial time series to reflect discontinuities of asset returns. Some of the most well known jump-diffusion models for the dynamics of foreign exchange include: 1) Merton’s Jump Model, 2) Conditional Heteroscedasticity and Jump model and Mean-Reversion, Conditional Heteroscedasticity and Jump model. The Merton’s Jump Model is given by the stochastic differential equation
is Brownian Motion driving the given asset prices [2] . It is known that jump-diffusion models are more realistic for studying the dynamics of exchange rates [3] . Dating back from the introduction of jump-diffusion process by [4] [5] as a tool for modelling the prices of options based on more general processes of underlying asset returns, jump-diffusion processes have also been widely used in modelling the dynamics of exchange rates. Empirical evidence based on simple jump-diffusion models suggests that jumps really form significant com- ponents of foreign exchange rate processes [1] [3] . As such, it is reasonable that both empirical and theoretical studies of exchange rates under uncertainty should allow for the presence of discontinuities explicitly. There has been a wide use of jump-diffusion processes to model financial time series to reflect discontinuities of asset returns. Some of the most well known jump-diffusion models for the dynamics of foreign exchange include: 1) Merton’s Jump Model, 2) Conditional Heteroscedasticity and Jump model and Mean-Reversion, Conditional Heteroscedasticity and Jump model. The Merton’s Jump Model is given by the stochastic differential equation 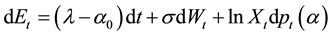 where Et is the exchange rate, λt is the instantaneous expected return, σ is the instantaneous volatility of the asset’s return subject to the Poisson jump not occurring, Wt is the Gauss- Wiener process,
where Et is the exchange rate, λt is the instantaneous expected return, σ is the instantaneous volatility of the asset’s return subject to the Poisson jump not occurring, Wt is the Gauss- Wiener process, 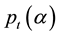 is a Poisson process which is independent and identically distributed over time, α is the intensity parameter of Poisson distribution,
is a Poisson process which is independent and identically distributed over time, α is the intensity parameter of Poisson distribution, 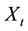 is the random jump size with
is the random jump size with 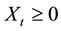 and
and ,
, 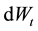 are statistically independent. This model explicitly allows for the presence of asymmetric lognormal jumps to the exchange rate. 3) The Conditional Heteroscedasticity and Jump model, is described by the stochastic dif- ferential equation
are statistically independent. This model explicitly allows for the presence of asymmetric lognormal jumps to the exchange rate. 3) The Conditional Heteroscedasticity and Jump model, is described by the stochastic dif- ferential equation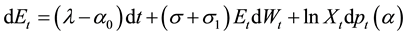 , which is an extension of Merton’s model and allows for conditional heteroscedasticity in addition to jumps. 4) Lastly, the Mean-Reversion, Conditional Heteroscedasticity and Jump model, described by the differential equation
, which is an extension of Merton’s model and allows for conditional heteroscedasticity in addition to jumps. 4) Lastly, the Mean-Reversion, Conditional Heteroscedasticity and Jump model, described by the differential equation ![]() where
where![]() . This model has a linear drift term in Et which makes it possible to capture the mean-reversion feature of the underlying process in addition to conditional heteroscedasticity and asymmetric jumps. The aim of our work is to provide further evidence for appropriateness of jump models. We do that by formulating an exchange rate model in terms of the general semimartingale on filtered probability space
. This model has a linear drift term in Et which makes it possible to capture the mean-reversion feature of the underlying process in addition to conditional heteroscedasticity and asymmetric jumps. The aim of our work is to provide further evidence for appropriateness of jump models. We do that by formulating an exchange rate model in terms of the general semimartingale on filtered probability space ![]() to model the dynamics of the exchange rate
to model the dynamics of the exchange rate ![]() where
where![]() . Our approach leads to general formulae which capture both the continuous and jump-diffusion cases models depending on whether
. Our approach leads to general formulae which capture both the continuous and jump-diffusion cases models depending on whether![]() , the continuous model or
, the continuous model or![]() , the jump diffusion one. The approach utilizes the specific market model called the Black-Scholes Quanto model, in other words, we consider products denominated in a currency other than those in which they are traded. Our prime interest is to price the claim CT, which in our case is the European call option, in this market when the dynamics of the exchange rate is being modelled by the general semimartingale as described above.
, the jump diffusion one. The approach utilizes the specific market model called the Black-Scholes Quanto model, in other words, we consider products denominated in a currency other than those in which they are traded. Our prime interest is to price the claim CT, which in our case is the European call option, in this market when the dynamics of the exchange rate is being modelled by the general semimartingale as described above.
2. The Model
We consider the quanto market model consisting of Dollar bond![]() , Sterling bond
, Sterling bond![]() , Sterling risky asset price
, Sterling risky asset price ![]() and the Exchange rate
and the Exchange rate ![]() on the filtered probability
on the filtered probability
space ![]() where
where![]() , and
, and![]() ,
, ![]() is the natural filtra-
is the natural filtra-
tion generated by the stock price process while![]() ,
, ![]() is the natural filtration generated by the exchange rate process.
is the natural filtration generated by the exchange rate process. ![]() describes information about prices and the exchange rate revealed to investors. We assume that the probability space
describes information about prices and the exchange rate revealed to investors. We assume that the probability space ![]() satisfies the usual conditions i.e the σ-field
satisfies the usual conditions i.e the σ-field ![]() is
is ![]() -complete and every
-complete and every ![]() contains all
contains all ![]() -null sets of
-null sets of![]() .
. ![]() is the Brownian motion in- dependent of
is the Brownian motion in- dependent of ![]() and
and ![]() i.e
i.e ![]() is a cadlág process that admits the decomposition
is a cadlág process that admits the decomposition ![]() where
where ![]() (a process of bounded variation),
(a process of bounded variation), ![]() and
and![]() . For a dollar investor in the quanto market defined in this problem, we want to find what is the price of the European call option having strike price k and strike time t?
. For a dollar investor in the quanto market defined in this problem, we want to find what is the price of the European call option having strike price k and strike time t?
Converting into Dollars
Since our asset is in Sterling, we need first of all to find the Dollar equivalent of this asset. For convenience sake we let![]() .
. ![]() be the dollar value of the Sterling asset price given by
be the dollar value of the Sterling asset price given by
![]() (1)
(1)
Define
![]() (2)
(2)
where
![]() (3)
(3)
![]() is a semimartingale since it is the sum of two semimartingales
is a semimartingale since it is the sum of two semimartingales ![]() and
and![]() . This in turn implies that
. This in turn implies that ![]() is a semimartingale. Let
is a semimartingale. Let
![]()
Then, using Ito’s formula for semimartingales [6] [7] , the dynamics of the dollar value for the Sterling risky asset is
![]() (4)
(4)
where
![]() (5)
(5)
(see Appendix). Let ![]() so that
so that ![]() then
then ![]() and
and
![]()
![]() being a semimartingale has the form
being a semimartingale has the form
![]() (6)
(6)
It is important to take note that superscript ![]() in
in ![]() is used to stress that
is used to stress that ![]() is the martingale part for process
is the martingale part for process ![]() which in this case
which in this case
![]() (7)
(7)
Since ![]() is a local martingale, it can be decomposed as
is a local martingale, it can be decomposed as
![]() (8)
(8)
where ![]() is the continuous part and
is the continuous part and ![]() is the discontinuous part of
is the discontinuous part of![]() . For more details and a proof of Equation (8) see [8] . Since
. For more details and a proof of Equation (8) see [8] . Since![]() , we have
, we have![]() . From Equation (6), we have
. From Equation (6), we have![]() . Similarly if we let
. Similarly if we let ![]() to be the continuous martingale part of
to be the continuous martingale part of ![]() then
then
![]() (9)
(9)
Now, using the bilinear property of sharp bracket process [9] , we obtain
![]() (10)
(10)
We further note that
![]()
This is true because μt, and σWt are continuous processes. It then follows that
![]() (11)
(11)
Substituting Xt and Equations (3), (10), (11) into Equation (5) we have
![]() (12)
(12)
Similarly, let Zt be the dollar value of the Sterling bond given by
![]()
Let
![]() (13)
(13)
It clearly follows that
![]() (14)
(14)
Noting that
![]() (15)
(15)
Note that Equation (15) follows because us is a continuous function so that![]() . The continuous martingale part of
. The continuous martingale part of ![]() is
is
![]()
Hence
![]()
Zt can now be written as
![]()
Its differential form, the dynamics of the dollar value of the Sterling bond can be written as
![]()
Which can be written as
![]() (16)
(16)
where
![]() (17)
(17)
And
![]()
For our analysis, we need to express the decompositions ![]() (Equation (12)) and
(Equation (12)) and ![]() (Equation (17)), in stochastic integral form, hence we use the random measure of jumps.
(Equation (17)), in stochastic integral form, hence we use the random measure of jumps.
In our case, we have
![]() (18)
(18)
And from Equation (10) we have
![]()
Hence, process of bounded variation ![]() can be express as
can be express as
![]() (19)
(19)
where A is as defined in Equation (6) and D is the process of bounded variation for the semimartingale Ht. We can express these results in canonical form by using the random measure of jumps (see [7] ). From Equation (5),
![]() (20)
(20)
Now, if we assume that![]() , then
, then
![]() (21)
(21)
where
![]() (22)
(22)
Now if we substitute Equations (9) (10) and (19) into Equation (21) we obtain
![]() (23)
(23)
where
![]() (24)
(24)
i.e.
![]() (25)
(25)
where ![]() and
and ![]() is a predictable process. Similarly from Equation (13)
is a predictable process. Similarly from Equation (13)
If we set ![]() with
with ![]() as a truncation function, we have
as a truncation function, we have![]() ,
,
![]() ,
, ![]() and together with Equation (17),
and together with Equation (17),
![]() (26)
(26)
where
![]()
This means the dynamics in our market model are modeled by the equations can also be presented by the eququations
![]() (27)
(27)
where ![]() and
and ![]() are as defined in Equations (21) and (26) respectively. Before we proceed we need to show that our market model defined by the system of Equation (27) does not entertain arbitrage opportunities.
are as defined in Equations (21) and (26) respectively. Before we proceed we need to show that our market model defined by the system of Equation (27) does not entertain arbitrage opportunities.
3. Arbitrage
A question we must ask before we proceed is whether the market (27) allows arbitrage opportunities or not. In this market, an investment strategy or portfolio is a predictable process
![]() (28)
(28)
Such that
![]() (29)
(29)
![]() denote the fractions of total wealth invested in B, z, and Y respectively at time t. The condition in
denote the fractions of total wealth invested in B, z, and Y respectively at time t. The condition in
inequality (29) ensures that the integrals ![]() make sence and are is a martingales.
make sence and are is a martingales.
Let
![]() (30)
(30)
be the worth the worth process. We need to know if our portfolio ![]() is self-financing. A portfolios is self-financing if
is self-financing. A portfolios is self-financing if ![]() can also be written as
can also be written as
![]() (31)
(31)
or in differential form, if
![]() (32)
(32)
Equations (31) and (32) imply that the portfolio is self-financing if changes in the value of the portfolio on an infinitesimal interval are due entirely to the changes in value of assets and not to an injection (or removal) of wealth from outside.
To show that our portfolio is self-financing, we use Lemma (5.1.3) in [2] . According to [2] , ![]() is a self- financing portfolio if
is a self- financing portfolio if
![]() (33)
(33)
where![]() , the discounted value of the wealth process.
, the discounted value of the wealth process.
![]()
This means
![]() (34)
(34)
Satisfying Equation (33). Hence ![]() is a self-financing portfolio. If in additional to this to (34),
is a self-financing portfolio. If in additional to this to (34), ![]()
as defined in Equation (34) above is lower bounded, then ![]() is said to be admissible. It is written as
is said to be admissible. It is written as![]() .
.
If ![]() is not admissible, it is not hard to construct doubling strategies, that is, a portfolio that attains arbitrarily large values of wealth with probability one when
is not admissible, it is not hard to construct doubling strategies, that is, a portfolio that attains arbitrarily large values of wealth with probability one when![]() , starting with zero initial capital at
, starting with zero initial capital at![]() , a situation we are avoiding. We first of all show that in this market,
, a situation we are avoiding. We first of all show that in this market, ![]() is an admissible strategy. The dynamic
is an admissible strategy. The dynamic ![]() for the dollar value of the sterling bond is given by the equation
for the dollar value of the sterling bond is given by the equation
![]()
Similarly, the dynamic ![]() for the dollar value of the Sterling risky asset is given by the equation
for the dollar value of the Sterling risky asset is given by the equation
![]()
From Equation (30)
![]() (35)
(35)
Since the portfolio ![]() is self-financing (Equation (32)), then
is self-financing (Equation (32)), then
![]()
Then
![]()
This means the differential form of of the dynamics of the discounted wealth process is
![]()
Hence the discounted wealth process will be
![]()
From the above equations, ![]() is a lower bounded process. It follows that
is a lower bounded process. It follows that ![]() is lower bounded implying that
is lower bounded implying that ![]() is an admissible strategy.
is an admissible strategy.
Definition 1 A portfolio ![]() is called arbitrage if
is called arbitrage if
![]() (36)
(36)
Since the portfolio ![]() in our market is admissible, we really claim there are no arbitrage opportunities in the market. The following discussion is a build up towards the proof to justify this claim.
in our market is admissible, we really claim there are no arbitrage opportunities in the market. The following discussion is a build up towards the proof to justify this claim.
3.1. Converting Yt into a Martingale
Our stock price process as described in Equation (27) is a semimartingale. To use the martingale approach, we need to convert the price process into a martingale by finding another probability space ![]() equivalent to our probability
equivalent to our probability ![]() so that Yt becomes a martingale. Now we consider our price process
so that Yt becomes a martingale. Now we consider our price process
![]() (37)
(37)
(see Equation (27)). ![]() and with Equation (2), we can say
and with Equation (2), we can say
![]() (38)
(38)
This means our price process is a local martingale iff ![]() is a local martingale. Now
is a local martingale. Now ![]() (
(![]() ) becomes a local martingale through the change of probability measure theorem for semimartingales i.e. we find another measure
) becomes a local martingale through the change of probability measure theorem for semimartingales i.e. we find another measure ![]() under which Yt becomes a martingale. To achieve this, we consider the following:
under which Yt becomes a martingale. To achieve this, we consider the following:
Suppose we have the triplet ![]() for a semimartingale x under measure
for a semimartingale x under measure ![]() what are the triplets
what are the triplets ![]() for semimartingale under a new probability measure
for semimartingale under a new probability measure![]() ?
?
Using the Gisanov’s Theorem for semimartingales,
![]() (39)
(39)
where ![]() satisfies the equation
satisfies the equation
![]() (40)
(40)
And ![]() is defined by the equation
is defined by the equation
![]() (41)
(41)
where ![]() is the positive measure on
is the positive measure on ![]() de- fined by
de- fined by
![]() (42)
(42)
where ![]() is a nonnegative function on
is a nonnegative function on ![]() (for
(for ![]() see [8] ).
see [8] ). ![]() is, by
is, by
definition, the ![]() -a.s unique
-a.s unique ![]() -measurable function
-measurable function ![]() with property
with property
![]() (43)
(43)
For all non-negative ![]() -measurable functions
-measurable functions![]() . This means that under measure
. This means that under measure![]() , the semi- martingale process
, the semi- martingale process ![]() evolves according to the equation
evolves according to the equation
![]() (44)
(44)
where
![]() (45)
(45)
And
![]() (46)
(46)
![]() is a
is a ![]() -Brownian motion [10] .
-Brownian motion [10] .
We start by finding the values β and ![]() for our case. To do this we first find
for our case. To do this we first find![]() , the continuous martingale part for the risky asset process Yt, as described by Equation (2). Using Itó’s formula for semimartingales, we have
, the continuous martingale part for the risky asset process Yt, as described by Equation (2). Using Itó’s formula for semimartingales, we have
![]()
It is easy to see that the continuous part of the semimartingale ![]() is given by
is given by
![]() (47)
(47)
Hint: in our calculations, we have made use of Equation (2) and the canonical decomposition of the semi- martingale hence the differential form of ![]() in our case can be written as
in our case can be written as
![]() (48)
(48)
From Equation (47) and using properties of conditional quadratic variation process for stochastic integrals with respect to semimartingales
![]() (49)
(49)
Now
![]() (50)
(50)
We can deduce from equating Equations (49) and (50), that Equation (40) can only hold if![]() , which is adopted as our choice of
, which is adopted as our choice of ![]() in this study. From the Equation (43) given by
in this study. From the Equation (43) given by
![]()
And the Equation (42) which simplifies below
![]()
We arrive at a choice of ![]() given by
given by
![]() (51)
(51)
Hence from Equation (46)
![]() (52)
(52)
Now under ![]()
![]() (53)
(53)
(see [8] )
From Equation (44),
![]() (54)
(54)
But in our case, to really achieve the case![]() , we make the following assumption: The process
, we make the following assumption: The process ![]() has bounded variation. Provided this assumption holds and that the conditions of lemma (2.13) in [11] are satisfied, then
has bounded variation. Provided this assumption holds and that the conditions of lemma (2.13) in [11] are satisfied, then
![]() (55)
(55)
It is also important to take note that from the assumption we have made and lemma (2.13) in [11] above, ![]() is exponentially special i.e.
is exponentially special i.e. ![]() is a special semimartingale. Now
is a special semimartingale. Now
![]() (56)
(56)
(see [12] ) and from Equation (55)
![]() (57)
(57)
From Equation (38)
![]() (58)
(58)
This means that under ![]()
![]() (59)
(59)
Which is a martingale process.
This means that since our market has an equivalent local martingale measure ![]() then by by the First Fundamental Theorem of Asset Pricing, there is no arbitrage in our market model ([13] ).
then by by the First Fundamental Theorem of Asset Pricing, there is no arbitrage in our market model ([13] ).
3.2. Equivalent Local Martingale Measures (ELMM)
In our previous section (section 3.1), we have proved the existence of ELMM ![]() and hence that the market is arbitrage free. But the question we really need to ask is whether or not
and hence that the market is arbitrage free. But the question we really need to ask is whether or not ![]() is a unique measure.? One of the major problems of financial markets with jumps is that they are typically incomplete. The martingale measure
is a unique measure.? One of the major problems of financial markets with jumps is that they are typically incomplete. The martingale measure ![]() is no longer unique as compared to complete market situation and in this case different martingale measures
is no longer unique as compared to complete market situation and in this case different martingale measures ![]() lead to different strategies. There are more than one ELMM, in fact infinitely many. The question is that which one of them should one use in the pricing formula. To answer our question it turns out that there is a minimal entropy martingale measure
lead to different strategies. There are more than one ELMM, in fact infinitely many. The question is that which one of them should one use in the pricing formula. To answer our question it turns out that there is a minimal entropy martingale measure ![]() such that the optimal strategy for
such that the optimal strategy for ![]() can be computed in terms
can be computed in terms![]() . The following discussion gives the definition of minimal martingale measure.
. The following discussion gives the definition of minimal martingale measure.
Minimal Relative Entropy Martingale Measure (MEMM)
Let ![]() be a set of all equivalent martingale measures of
be a set of all equivalent martingale measures of![]() .
.
Definition 2 ![]() is said to be minimal entropy martingale measure (MEMM) of
is said to be minimal entropy martingale measure (MEMM) of ![]() if it satisfies the follow- ing formula
if it satisfies the follow- ing formula
![]()
where ![]() is the relative entropy of
is the relative entropy of![]() , which is given by the following formula
, which is given by the following formula
![]() (60)
(60)
(see [14] [15] ).
The relative entropy measures the minmal departure from a given measure![]() . The relative entropy
. The relative entropy ![]() is always non-negative and
is always non-negative and ![]() is equivalent to
is equivalent to![]() .
.
The minimal martingale measure ![]() is uniquely determined as discussed in [14] [15] .
is uniquely determined as discussed in [14] [15] .
Let ![]() be as defined in Equation (28). We assume that the process
be as defined in Equation (28). We assume that the process ![]() is pre- dictable while
is pre- dictable while ![]() and
and ![]() are adapted. Hence Equation (37) takes the form
are adapted. Hence Equation (37) takes the form
![]() (61)
(61)
where ![]() is now a martingale.
is now a martingale.
Now solving (61) above gives
![]() (62)
(62)
where ![]() is the Dolĕans Dade stochastic exponential.
is the Dolĕans Dade stochastic exponential.
![]()
Now
![]() (63)
(63)
And
![]()
(see Equation (10)). Hence
![]() (64)
(64)
(for ![]() compare with Equation (13), page 666 in [7] )
compare with Equation (13), page 666 in [7] )
Hence
![]() (65)
(65)
The process![]() , in Equation (65) above, is a martingale and it is under a new probability measure
, in Equation (65) above, is a martingale and it is under a new probability measure![]() . This equation marks one of the major contributions of this study to the the theory option pricing through martingale approach in the sense that it accommodates both continuous and jump cases. In the situation where
. This equation marks one of the major contributions of this study to the the theory option pricing through martingale approach in the sense that it accommodates both continuous and jump cases. In the situation where![]() , then
, then ![]() and Equation (65) becomes
and Equation (65) becomes
![]() (66)
(66)
which is the continuous and most familiar case, while if ![]() then we have a jump case. The equation brings with it the convenience of converting the stock price into a martingale whenever we are using a martingale approach as in any of the cases, the process of converting the process into a martingale, simplifies to mere calculation of
then we have a jump case. The equation brings with it the convenience of converting the stock price into a martingale whenever we are using a martingale approach as in any of the cases, the process of converting the process into a martingale, simplifies to mere calculation of![]() ,
, ![]() and
and ![]() and substitute into Equation (65).
and substitute into Equation (65).
3.3. The Price of European Call Option
We now come to the question fundamental of this study.
How much should the investor be willing to pay for a European call option at t = 0 in the case where Yt is a semimartingale process as defined in Equation (65)?. We extend the theorem which was given in [16] .
Theorem 1 Let![]() , with its canonical decomposition as shown in Equation (59) above, be a process with independent increment, and assume that
, with its canonical decomposition as shown in Equation (59) above, be a process with independent increment, and assume that![]() ,
, ![]() and
and ![]() exist where
exist where![]() . Then the following integro-differential equation holds:
. Then the following integro-differential equation holds:
![]() (67)
(67)
Proof. Before we proceed, we take note of the following:
![]()
This means that ![]() where
where
![]()
The theory of pricing of the European call option (see [17] ) and the Markovian property of![]() , the value of the European call option at time T is given by
, the value of the European call option at time T is given by
![]()
where ![]() is given by
is given by
![]()
□
But how do we evaluate the value ![]() in our case. By using the Markovian property of
in our case. By using the Markovian property of ![]() we applying Ito’s formula to
we applying Ito’s formula to ![]() and obtain
and obtain
![]()
![]()
Now using the fact that a predictable local martingale with finite variation starting at zero is zero (theorem leads us to the equation i.e.
![]()
4. Examples
4.1. Example 1: Continuous Case
Suppose ![]()
From Equation (3),
![]() (68)
(68)
where ![]() is the Brownian Motion on the same stochastic basis
is the Brownian Motion on the same stochastic basis ![]() as Brownian Motion
as Brownian Motion ![]() and that these Brownian Motions are correlated with correlation co-efficient ρ. Obviously, from Equation (68),
and that these Brownian Motions are correlated with correlation co-efficient ρ. Obviously, from Equation (68),![]() .
.
![]() (69)
(69)
Note that U, as it is defined in Equation (69), is an element of Borel sets which do not have a 0 element. Since ![]() and 0 cannot be an element of u justifies Equation (69).
and 0 cannot be an element of u justifies Equation (69).
It follows that
![]() (70)
(70)
Similarly
![]() (71)
(71)
From Equations (39) and (51)), under measure![]() ,
,
![]() (72)
(72)
And![]() . Hence from Equation (64)
. Hence from Equation (64)
![]()
Hence![]() ,
, ![]() and
and![]() . Using theorem (1) with
. Using theorem (1) with ![]() and
and ![]() leads to equation
leads to equation
![]() (73)
(73)
And hence (from the same theorem)
![]() (74)
(74)
4.2. Example 2: Process with Jump
Suppose in our model, the exchange rate is not continuous and is modeled by the stochastic differential equation
![]() (75)
(75)
where ![]() is the
is the ![]() -Brownian Motion process, Mt is the compensated
-Brownian Motion process, Mt is the compensated ![]() -martingale process associated with the Poisson process Nt (with intensity
-martingale process associated with the Poisson process Nt (with intensity![]() ) i.e.
) i.e. ![]() and is independent of the Brownian motion Nt. We choose
and is independent of the Brownian motion Nt. We choose ![]() to be a Gaussian process with independent increments, independent to both
to be a Gaussian process with independent increments, independent to both ![]() and Nt. We let
and Nt. We let ![]() and
and![]() . Assume that
. Assume that![]() ,
, ![]() ,
,![]() . We further assume that
. We further assume that ![]() is inde- pendent of Wt where Wt is the Brownian motion as defined in Equation (3).
is inde- pendent of Wt where Wt is the Brownian motion as defined in Equation (3).
To find out what our Xt and![]() , are in this case we first of all solve our equation.
, are in this case we first of all solve our equation.
![]() (76)
(76)
Using Itó’s formula for processes with jumps, we let
![]()
![]()
From which we obtain
![]()
And
![]() (77)
(77)
Hence from Equation (77), we obtain ![]() given by
given by
![]()
Clearly, ![]() (since
(since![]() ). From Equation (2), we obtain
). From Equation (2), we obtain
![]() (78)
(78)
From (78) we obtain the process of the form
![]() (79)
(79)
Equation (79) yields the sharp bracket process for ![]() of the form
of the form
![]()
And hence under measure![]() ,
,
![]() (80)
(80)
Clearly ![]() (80) is a process with independent increments (as it is the sum of processes with independent increments), hence we can find a deterministic function
(80) is a process with independent increments (as it is the sum of processes with independent increments), hence we can find a deterministic function![]() , a deterministic measure-valued function
, a deterministic measure-valued function ![]() and a deterministic increasing function
and a deterministic increasing function ![]() such that
such that![]() ,
, ![]() (Jacod and Shiryaev [8] ).
(Jacod and Shiryaev [8] ). ![]() is also a Lèvy process , we can choose
is also a Lèvy process , we can choose![]() , c to be a constant and
, c to be a constant and ![]() (the Levy measure) (see section). In addition,
(the Levy measure) (see section). In addition, ![]() where
where ![]() and
and ![]() is the distribution of the jump size of less than 1, i.e. from this we can deduce that the expected number of jumps, in time interval 1 is
is the distribution of the jump size of less than 1, i.e. from this we can deduce that the expected number of jumps, in time interval 1 is ![]() and the jump size is distributed according to F. If we let
and the jump size is distributed according to F. If we let ![]() then
then![]() . Since
. Since ![]() is a Gaussian process with
is a Gaussian process with ![]() and
and![]() , Then
, Then
![]()
And
![]()
From Equation (80),
![]()
And
![]() (81)
(81)
Hence from theorem (1), ![]() is found by solving the equation
is found by solving the equation
![]() (82)
(82)
And
![]()
4.3. Example 3: Ht a Cumulative Process
We consider a situation where the exchange rate is ![]() where
where ![]() and
and ![]() are independent processes. In this case
are independent processes. In this case![]() . This means that
. This means that
![]()
In this case
![]()
This means that
![]()
Hence Equation (80) becomes
![]() (83)
(83)
This means ![]() is the solution of the integro-differential equation
is the solution of the integro-differential equation
![]() (84)
(84)
With
![]()
5. Discussion
Equation (73) compares well with Equation (82) in the sense that (82) without the term
![]() (85)
(85)
Gives Equation (73). This means that Equation (85) is the contribution of the jump to the price of the option. The effects of the jumps on the price of the the option can be easily observed from this Equation (82) through the role![]() , which is the jump parameter in this equation. For example in the case where
, which is the jump parameter in this equation. For example in the case where![]() , we
, we
![]()
Hence Equation (82) is reduced to Equation (73) which is a continuous case. This can be further justified from the definition of our![]() .
. ![]() and hence
and hence ![]() i.e.
i.e. ![]() if
if![]() , justifying why case (2) in section (4.2) is reduced to case (1) in section (4.1) and at the same time confirming why Equation (82) degenerates to equation (73). We also take note that the co-domain of the function
, justifying why case (2) in section (4.2) is reduced to case (1) in section (4.1) and at the same time confirming why Equation (82) degenerates to equation (73). We also take note that the co-domain of the function ![]() is
is![]() . This means
. This means ![]() is not taking negative values hence has a positive effect to the value of the option. The positive effect of
is not taking negative values hence has a positive effect to the value of the option. The positive effect of ![]() is in the sense that as far as
is in the sense that as far as
![]()
In Equation (82), the increase in ![]() will mean the increase in the price of the option In the same vein,
will mean the increase in the price of the option In the same vein, ![]() depends on
depends on ![]() as
as ![]() hence we expect
hence we expect ![]() as
as ![]() takes positive values. This means
takes positive values. This means ![]() has a positive effect in Equation (82), emphasizing the effects of
has a positive effect in Equation (82), emphasizing the effects of![]() .
.
We also take note that expression (85) is also equal to zero if either ![]() (the case which we have just discussed),
(the case which we have just discussed), ![]() (the same case since
(the same case since ![]() (in our case) if and only if
(in our case) if and only if![]() ) or if
) or if
![]()
A case which can be handled numerically.
6. Conclusion
The method gives the general method of calculating the price of the option in the sense that it accommodates both continuous and processes with jumps. When![]() , we are talking of continuous processes as shown by example 1 and when
, we are talking of continuous processes as shown by example 1 and when ![]() we are talking of processes with jumps. This can provide a more general way of finding the price of an option.
we are talking of processes with jumps. This can provide a more general way of finding the price of an option.
Appendix
Then, using Ito’s formula for semimartingales (Protter [6] ), we have
![]() (86)
(86)
And in differential form, this can be expressed as
![]()