On the Advantages of the Theories of Plasticity with Singular Loading Surface ()
1. Introduction
The overwhelming majority of the theories of plastic deformation of metals address the notion of yield and loading surface to give a geometrical interpretation of the onset and development of plastic strains. This paper will analyze (i) plastic flow theories with smooth loading surfaces and (ii) results obtained in terms of the synthetic theory of irrecoverable deformation for the case of a non-proportional loading. Consider a loading path
consisting of two parts in stress space (Figure 1): AB—proportional loading 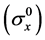 beyond the yield limit of material in uniaxial tension
beyond the yield limit of material in uniaxial tension  and BC—infinitesimal additional loading
and BC—infinitesimal additional loading  at right angle to AB potion. According to Sveshnikova [1] , such loading regimes result in the increment of plastic deformation
at right angle to AB potion. According to Sveshnikova [1] , such loading regimes result in the increment of plastic deformation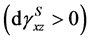 .
.
Sveshnikova’s experiments were carried out on thin-walled cylinders loaded in uniaxial tension and the additional loading was obtained by the twisting of the specimens.
![]()
Figure 1. Loading path ABC in Sveshnikova’s experiment.
The goal of the paper is to show that the synthetic theory is capable of describing the occurrence of the increment of plastic deformation due to the additional loading, whereas the theories with smooth loading surfaces lead to the absence of plastic flow, which is contradictive to the experimental results. Although the problem dates back to the 20th century, it remains unsolved till now. The issue of the occurrence of plastic deformation due to an infinitesimal additional loading, nevertheless, is of high importance. Indeed, as is often the case, structural members working under some stress state are subjected to a small additional loading resulted from sudden overloading or lack of fit. Such a situation is typical, e.g. beams deformed by bending and undergoing small torsions.
The occurrence of the increments of plastic strains due to the additional loading is studied in a geometrical way, by means of the analysis of loading surfaces. In terms of the synthetic theory [2] [3] , an additional orthogonal loading leads to the occurrence of additional plastic deformation (which can be calculated by the formulae presented in [2] [3] ), which is not the case in the framework of the theories providing smooth loading surfaces.
2. Smooth Loading Surface under Two-Sectional Loading Path
Consider the behavior of material modeled by the flow theories based on the isotropic and kinematic hardening rule [3] - [6] for the following loading path (as shown in Figure 1): uniaxial tension and subsequent orthogonal additional loading (infinitesimal torsion).
In isotropic hardening, the yield surface increase in size due to the stress vector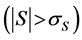
 , but remain the
, but remain the
same shape, as a result of plastic straining (Figure 2(a)). This condition in the three dimensional subspace, 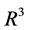 , of the Ilyushin five-dimensional space
, of the Ilyushin five-dimensional space 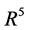 [3] [5] , can be expressed as
[3] [5] , can be expressed as
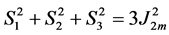 (1)
(1)
where  is the maximum value of the second invariant of stress deviator tensor
is the maximum value of the second invariant of stress deviator tensor 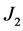 [4] for the whole history of loading.
[4] for the whole history of loading.
According to kinematic hardening rule, the yield surface remains the same shape and size but merely translates in stress space (Figure 2(b)), which can be expressed by the following equation:
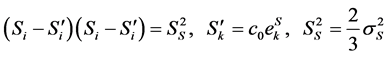 (2)
(2)
where 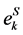 is the plastic strain vector components [3] [5] ,
is the plastic strain vector components [3] [5] , 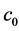 constant.
constant.
Equations (1) and (2) give the von-Mises yield criterion when 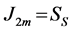 and
and ![]() respectively, and
respectively, and ![]()
![]() are the components of stress vector,
are the components of stress vector, ![]() , which expresses loading. The components
, which expresses loading. The components ![]() are con- verted from the stress deviator tensor components acting at a point of body
are con- verted from the stress deviator tensor components acting at a point of body ![]() as follows [2] [3] :
as follows [2] [3] :
![]() (3)
(3)
where ![]() is the Kronecker’s delta The length of vector
is the Kronecker’s delta The length of vector ![]() is related to the second invariant of stress deviator tensor,
is related to the second invariant of stress deviator tensor, ![]() , as
, as![]() .
.
Now, consider the infinitesimal additional loading![]() ,
,![]() . It is easy to see that in both case the vector
. It is easy to see that in both case the vector ![]() lies on the tangent drawn through a loading-point, the endpoint of the vector
lies on the tangent drawn through a loading-point, the endpoint of the vector![]() , i.e. it is perpendicular to
, i.e. it is perpendicular to
![]()
Figure 2. Direction of additional loading vector dS (0, 0, dτxz) with respect to the loading surface in terms of isotropic (a) and kinematic (b) hardening rule in S1 - S3 coordinate planes.
S1-axis (Figure 2(a) and Figure 2(b)). In terms of flow plasticity theories, this means that the additional loading ![]() is a neutral loading resulting in no plastic strain increment. Therefore, the
is a neutral loading resulting in no plastic strain increment. Therefore, the ![]() vector-increment does not induce the increment in plastic deformation, which contradicts the result obtained by Sveshnikova.
vector-increment does not induce the increment in plastic deformation, which contradicts the result obtained by Sveshnikova.
Therefore, although the theories discussed above are widely used for the modelling of the plastic strains of metals, they are incapable of catching the phenomenon registered in [1] .
3. Fundamentals of the Synthetic Theory
The synthetic theory is based on the Batdorf-Budiansky slip concept [7] and the Sanders flow theory [8] and deals with small irrecoverable (plastic/creep) deformations of hardening materials.
Similarly to the Batdorf-Budiansky concept, the deformation of material is calculated on its two structural levels: macro- and micro-level. A point of a body is considered as an elementary volume of the body,![]() . The volume
. The volume ![]() consists of a large quantity of microvolumes (grains),
consists of a large quantity of microvolumes (grains), ![]() , each being an element of the continuous, capable of deforming under the applied forces (Figure 3). The mechanism of irrecoverable deformation within the microvolume
, each being an element of the continuous, capable of deforming under the applied forces (Figure 3). The mechanism of irrecoverable deformation within the microvolume ![]() is slip of one part of
is slip of one part of ![]() in relation to another. It is assumed that the number of
in relation to another. It is assumed that the number of ![]() is so great (theoretically it tends to infinity) that every possible orientation of slip systems exists in volume
is so great (theoretically it tends to infinity) that every possible orientation of slip systems exists in volume![]() . Accordingly to Budiansky, the stress state in every volume
. Accordingly to Budiansky, the stress state in every volume ![]() (slip system) is the same as that in the volume
(slip system) is the same as that in the volume![]() . The stress acting in
. The stress acting in ![]() is obtained in a conventional way by solving the equilibrium equation of the body together with consistency and boundary conditions (the problem is the simplest for the case of e.g. tension, or torsion when a homogenous stress distribution is observed). It must be noted that, in contrast to a uniform distribution of the stress among microvolumes
is obtained in a conventional way by solving the equilibrium equation of the body together with consistency and boundary conditions (the problem is the simplest for the case of e.g. tension, or torsion when a homogenous stress distribution is observed). It must be noted that, in contrast to a uniform distribution of the stress among microvolumes![]() , the magnitude of slip strongly depends on the orientation of the slip system relative to the direction of the acting stresses. The total deformation in
, the magnitude of slip strongly depends on the orientation of the slip system relative to the direction of the acting stresses. The total deformation in ![]() is determined as the sum of micro-deformations developed in volumes
is determined as the sum of micro-deformations developed in volumes![]() .
.
The modeling of irrecoverable deformation at a point of a body ![]() takes place in the three-dimensional subspace
takes place in the three-dimensional subspace ![]() of the Ilyushin five-dimensional space of stress deviators,
of the Ilyushin five-dimensional space of stress deviators, ![]() [5] . The yield surface in
[5] . The yield surface in ![]() is a sphere of radius
is a sphere of radius![]() , which corresponds to the von-Mises yield criterion,
, which corresponds to the von-Mises yield criterion,
![]() (4)
(4)
where ![]() is the yield limit of material in uniaxial tension.
is the yield limit of material in uniaxial tension.
According to Sanders [8] , through each point on the sphere we draw a tangent plane. So, the yield surface can be thought of the inner envelope of the equidistant planes.
The position of plane in ![]() is defined by the following two quantities: (i) the unit vector
is defined by the following two quantities: (i) the unit vector ![]() normal to the plane and (ii) the distance from the origin of coordinates to the plane,
normal to the plane and (ii) the distance from the origin of coordinates to the plane, ![]() (in the virgin state,
(in the virgin state, ![]() in all directions). Since we work in
in all directions). Since we work in ![]() subspace, the projection of
subspace, the projection of ![]() -planes in
-planes in ![]() are considered, whose positions are defined by
are considered, whose positions are defined by ![]() and vector
and vector ![]() normal to plane in
normal to plane in ![]() (Figure 4). The orientation of
(Figure 4). The orientation of ![]() is established by spherical angles
is established by spherical angles ![]() and
and ![]() as shown in Figure 4, and a relationship between
as shown in Figure 4, and a relationship between ![]() and
and ![]() is
is![]() , where
, where ![]() is an angle between
is an angle between ![]() and
and ![]() [2] [3] .
[2] [3] .
To establish a hardening rule, which governs the kinetics of loading surface during plastic flow, we extend the provision that a surface can be constructed as an inner envelope of planes to the case of loading as well. In the
![]()
Figure 3. Two levels of material structure: an elementary volume of loaded body (V) consists of grains (slip systems) V0 producing deformation on microlevel.
![]()
Figure 4. Distance to plane HN and the orientation of vector m.
course of loading, the vector ![]() displaces on its endpoint a set of planes from their initial position, i.e. from sphere (4). Each plane moves without changing its orientation (Figure 5(a)). As a result, the loading surface—the inner envelope of the planes—has the form as shown in Figure 5(b). It consists of two parts: the cone whose lateral surface is formed by the boundary planes reached by the
displaces on its endpoint a set of planes from their initial position, i.e. from sphere (4). Each plane moves without changing its orientation (Figure 5(a)). As a result, the loading surface—the inner envelope of the planes—has the form as shown in Figure 5(b). It consists of two parts: the cone whose lateral surface is formed by the boundary planes reached by the![]() , and the part of sphere (4), which is the inner envelope of stationary planes.
, and the part of sphere (4), which is the inner envelope of stationary planes.
Each tangent plane corresponds to an appropriate slip system![]() , and the displacement of the plane on the endpoint of stress vector symbolizes the development of plastic micro-deformation within the slip system. Plastic microstrain modeled by the displacement of one plane is assumed to be a vector normal to the plane (see Figure 5(a)). It is easy to see that the distance to a plane gives the degree of the hardening of material. Actually, the greater
, and the displacement of the plane on the endpoint of stress vector symbolizes the development of plastic micro-deformation within the slip system. Plastic microstrain modeled by the displacement of one plane is assumed to be a vector normal to the plane (see Figure 5(a)). It is easy to see that the distance to a plane gives the degree of the hardening of material. Actually, the greater![]() , the greater stress vector needed to reach the plane, i.e. to induce plastic shift within the corresponding slip system.
, the greater stress vector needed to reach the plane, i.e. to induce plastic shift within the corresponding slip system.
As it follows from Equation (4) and the hardening rule, material is considered initially isotropic, but after the development of irrecoverable strain its properties (e.g. hardening) become definitely anisotropic.
The condition that a plane in ![]() is located on the endpoint of stress vector, i.e. that irrecoverable deformation develops within corresponding slip system, is expressed as
is located on the endpoint of stress vector, i.e. that irrecoverable deformation develops within corresponding slip system, is expressed as
![]() (5)
(5)
where the product ![]() plays the role of resolve stress acting within the slip system. The components
plays the role of resolve stress acting within the slip system. The components ![]() [2] [3]
[2] [3]
![]() (6)
(6)
An average measure of irrecoverable strain within one slip system![]() , irrecoverable strain intensity
, irrecoverable strain intensity![]() , is defined via
, is defined via ![]() as [2] [3] :
as [2] [3] :
![]() (a)
(a)![]() (b)
(b)
Figure 5. Displacement of plane on the endpoint of stress vector (a) and loading-surface (b) in terms of the synthetic theory.
![]() (7)
(7)
Macro-deformation is defined by a strain vector, ![]() , whose components (
, whose components (![]() ,
,![]() ) are calculated as the sum (three-fold integration) of nonzero strain intensities, i.e. only the planes displaced by the stress vector contribute to the value of macrostrain:
) are calculated as the sum (three-fold integration) of nonzero strain intensities, i.e. only the planes displaced by the stress vector contribute to the value of macrostrain:
![]() (8)
(8)
The upper and lower integration limits in (8) are obtained from the condition ![]() [2] [3] . The strain vector components can be converted to the strain-deviator tensor components,
[2] [3] . The strain vector components can be converted to the strain-deviator tensor components, ![]()
![]() , as
, as
![]() (9)
(9)
Summarizing, the magnitude of plastic deformation rate depends on the set of planes located on the endpoint of![]() , and the distances they traveled from the sphere (4).
, and the distances they traveled from the sphere (4).
4. Synthetic Theory for Two-Sectional Loading Path
Let us study if an additional plastic strain increment occurs due to the additional loading ![]() in terms of the synthetic theory. According to the principle of the forming of loading surface as the inner envelope of displaced planes, i.e. because of the forming a conical singularity at the loading point (the endpoint of stress vector
in terms of the synthetic theory. According to the principle of the forming of loading surface as the inner envelope of displaced planes, i.e. because of the forming a conical singularity at the loading point (the endpoint of stress vector![]() , point
, point![]() ), it is easy to see that the additional vector
), it is easy to see that the additional vector ![]() points outward the current loading surface (Figure 6).
points outward the current loading surface (Figure 6).
![]()
Figure 6. Orientation of additional stress-vector dS with respect to the loading surface in terms of the synthetic theory.
This fact means that the action of the ![]() induces the increment in plastic deformation:
induces the increment in plastic deformation:![]() . As shown in Rusinko’s early work [9] , the number of planes displaced by the
. As shown in Rusinko’s early work [9] , the number of planes displaced by the ![]() is a half of the planes locating on the endpoint of
is a half of the planes locating on the endpoint of![]() .
.
Therefore, in the framework of the synthetic theory, the phenomena of the occurrence of plastic deformation on the orthogonal portion of additional loading can be modelled, this fact is of great importance since is not the case for the flow theories with smooth loading surface.
5. Conclusion
The formation of corner point (conical singularity) on the loading surface during plastic straining is of crucial importance for the correct formulation of the theories of plasticity. As it has been shown in this paper, the flow plasticity theories based on hardening rules with smooth loading surfaces lead to non-conformity with the experimental result obtained for the case of non-proportional loadings (they give no increment in plastic strain), e.g. when the loading path is a broken line with orthogonal portions. At the same time, the synthetic theory of plastic deformation shows the occurrence of plastic straining in the additional loading even without calculations; it is immediately seen from the shape of loading surface and the direction of additional loading.
Acknowledgements
The authors expresses thanks to Prof. K. Rusinko (Budapest University of Technology and Economics, Hungary) for many useful conversations on the topics presented in this article.