Preparation, Characterization and Statistical Studies of the Physicochemical Results of Series of “B” Carbonated Calcium Hydroxyapatites Containing Mg²⁺ and CO^2-₃

S. Ben Abdelkader, F. Bel Hadj Yahia, I. Khattech

Applied Thermodynamics Laboratory, Chemistry Department, Faculty of Sciences, Tunis, Tunisia.

DOI: 10.4236/ajac.2014.514106                

Abstract

In this study, series of hydroxyapatites containing Mg²⁺ and CO^2-₃ are prepared by the precipitation method with independently varying concentrations of CO^2-₃ and Mg²⁺. All the compounds are characterized by infrared spectra (IR); powder X-ray diffraction (PXRD) and elemental analysis. The physical analysis results show that the prepared compounds are pure B-type carbonate apatite. The presence of Mg²⁺ and CO^2-₃ in the apatite cause the following effects on its physical properties: a decrease in a-dimension but no changes in c-dimension and a decrease in crystallinity as shown in XDR patterns and IR spectra. The results of the chemical analysis allow us to predict the predominant substitution mechanisms for the CO^2-₃ and the Mg²⁺ incorporations in the calcium hydroxyapatites and to calculate their relative contributions x, y and z.
(II);   2. (IV);   (V). Statistical studies of the results “multiple linear regression, analysis of variance (ANOVA) and t-test of the regression coefficients” allow us to determine and to test the mathematical model proposed. Finally, the present study makes it possible to write the general formula for these com-pounds.

Keywords

B-Type Carbonated Calcium Hydroxyapatite Containing Magnesium “B” CO₃Mg-HAps, Substitution Mechanism(s), Multiple Linear Regression, F-Test (ANOVA), t-Test of the Coefficients

1. Introduction

A number of studies have reported that the incorporation of magnesium in hydroxyapatites Ca₁₀(PO₄)₆(OH)₂ is limited [1] - [3] . Previously, it has been shown that the magnesium can disturb the crystallization of apatites when its concentration in the solution is sufficient to be a major competitor for calcium [4] . But when the molar ratio of Mg/Ca is higher than 0.1, another phase is observed, the whitlockite [3] [5] - [7] . The co-substitution of a second ionic species like the carbonate ion can increase the insertion of magnesium in the lattice and prevent the decomposition while stabilizing the structure [8] [9] .

On the other hand, it is now well established that the biological minerals are best described as carbonated apatites rather than as a hydroxyapatite [2] [10] - [12] . The carbonate presents at 3% - 6% in biological apatites, mostly substitutes for the phosphate ion in the crystal structure and has a significant influence on the incorporation of other foreign ions into the apatite lattice. Magnesium is one of the most abundant trace ions present in the biological hard tissues and in dental enamel, its content approximately being 0.1% - 0.4%. In dentin, the magnesium content is up to 1.1%, while in bone, it is found at 0.6% [13] - [15] . Thusly, Magnesium has been the subject of many studies. To understand the role of magnesium on biological apatites, the works using synthetic carbonated apatites are very helpful.

Previous studies suggest that the magnesium is incorporated into or onto the carbonated apatites during their formation [16] - [24] . Some of these works demonstrate the role of the carbonate concentration, the pH of preparation, and the magnesium content incorporated into the apatites at similar quantities to those found in biological apatites [16] [17] [23] . Other works report the effect of the magnesium on the parameters of the lattice of apatites prepared by precipitation or high-temperature synthesis [4] [25] . Legeros et al. [22] noted an increase in the dissolution rates, of carbonate-containing apatites when the magnesium was incorporated. Some studies have investigated the phase’s composition after heat-treatment of the magnesium/carbonate co-substituted in the hydroxyapatite [16] [23] [24] .

Despite numerous investigations, the mechanism(s) by which the carbonate and the magnesium are incorporated in the apatite lattice are not yet known. Indications are found in the literature about the mechanisms by

which 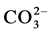and alkalimetal M⁺ are incorporated in the apatite lattice [26] - [28] . In these works, De Maeyer

and Verbeeck suggest that six fundamental substitution mechanisms can contribute theoretically for these substitutions .

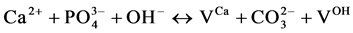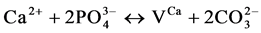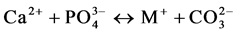(I)

(II)

(III)

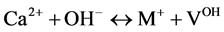(IV)

(V)

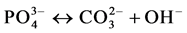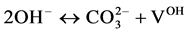(VI)

where V^X stands for a vacancy in the X-sublattice. The contributions of each of these mechanisms should be estimated on the basis of a thorough physicochemical studies of the samples.

The present study tries to find the mechanism(s) which contribute to the incorporation of magnesium and carbonate in the apatites lattice. For this purpose, series of “B” carbonated calcium hydroxyapatites containing

magnesium are prepared by the precipitation method. In the first series, the concentration of the 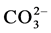solution

is C_c = 0.00 M while the Mg²⁺ concentration C_Mg is 0.00, 1.7, 6.8 and 13.6 mM. For the second, the same procedure is remade with C_c = 0.025 M in the hydrolysis solution and for the third, C_c is equal to 0.05 M. The chemical and physical characteristics of the samples prepared are determined and an attempt is made to deduce the fundamental substitution mechanisms which determine their stoichiometry. Finally, statistical studies of the experiment results allow us to find the relationship between the different variables and to verify the proposed mechanisms by which and Mg²⁺ are incorporated in the apatite lattice.

2. Methods and Materials

2.1. Preparation of “B” Type Carbonated Hydroxyapatites Containing Magnesium

The method of preparation used in this work is inspired from the method used in reference [23] but it is slightly modified. The apaties are prepared by dropping 200 mL of a phosphate solution (NH₄)₂HPO₄ (0.18 M) into 200 mL of a calcium solution Ca(NO₃)·4H₂O (0.44 M) under reflux at 87˚C. To the calcium solution is added 20 mL of a magnesium solution Mg(NO₃)₂·6H₂O containing different concentrations: C_Mg (0.00; 1.7; 6.8 and 13.6) mM. The same procedure is remade by adding to the phosphate solution 5 mL of a carbonate solution NH₄HCO₃ (1 M). A third set of preparations is performed by adding 10 mL from the above carbonate solution. The pH is maintained at 9.0 during the precipitation by adding an ammonia concentrated solution (28% weight). The precipitation is carried out over 3 h. Then, the system is refluxed for an additional duration of 2 h. The samples are filtered, thoroughly washed with hot distilled water and dried overnight at 120˚C.

2.2. Physical Analysis

The powdered samples are identified by X-ray diffraction and by infra red spectroscopy. Infrared spectra of the samples dispersed in KBr tablets are recorded using a Shimadzu Fourier transform infrared spectrophotometer in the range of 4000 - 400 cm⁻¹. Then, the samples are analyzed by X-ray diffraction (XRD) using a Philips diffractometer using Cu Ka radiation. The samples are scanned in the 2θ range of 20˚ - 60˚. The “a and c” parameters of the lattice of the hexagonal unit cell are calculated using “wincell” refinement program.

2.3. Chemical Analysis

The samples are analyzed for Ca, PO₄, CO₃ and Mg. The calcium content of the precipitates is determined by a complexometric titration with the ethylenediaminetetraacetic acid [29] , the magnesium by atomic absorption, the carbonate content is determined by coulometrically method and the phosphorus content by spectrophotometrie of the phosphomolybdate complex [30] .

3. Results

3.1. Results of Physical Analysis

The IR Spectra of some representative samples (Mg₄, Mg₈ and Mg₁₂) are shown in Figure 1. The spectra contain the characteristic bands of the phosphate group in the ranges 960 - 1100 and 570 - 610 cm⁻¹. Two broad bands, around 1635 cm⁻¹ and 3400 cm⁻¹, confirm that the samples contain a significant amount of water. On the

Figure 1. IR spectra of some representative samples.

spectra of the samples (Mg₈ and Mg₁₂) are displayed typical absorption bands of at ~873 and ~1420 cm⁻¹ and between 1450 and 1500 cm⁻¹, characterizing the vibration of the on lattice sites (B- type) [31] . From Figure 1, we can clearly see that the intensity of these absorptions increases with the increase of the carbonate content. On the other hand, the IR spectra of the compounds (Mg₄, Mg₈ and Mg₁₂) show that the magnesium incorporated in the apatites causes the loss of resolution of the absorptions bands suggesting a decrease in the crystallinity [31] .

The X-ray diffraction patterns of some representative samples are shown in Figure 2. The X-ray diffraction powder patterns of the compounds show only one crystal phase. The peaks are sharp, well resolved and characteristic of the hexagonal apatite phase. No extraneous peaks attributable to other phases than apatite could be found in the diffractograms. The increase of the level of substitution produces a loss of the resolution of the 112 peak and a decrease in the intensity of the 300, 202 and 002 peaks.

The Table 1 contains the values of the lattice parameters “a” and “c” obtained for the different compounds.

From this table, we can see that simultaneous incorporation of two elements “CO₃ and Mg” results in an decrease of the “a” parameter. This contraction is attributed to the simultaneous effects of the and Mg²⁺ substitutions [2] .

Figure 2. X-ray diffraction patterns of some representative samples.

Table 1. “a” and “c” Lattice parameters of “B” CO₃Mg-Haps.

3.2. Chemical Results

The results of the chemical analysis of the samples in Weight % are summarized in Table 2. This table also gives the hydroxide content of the samples calculated on the basis of the electroneutrality condition and the total mass balance ∑ % obtained from the equation:

(1)

With M_X the atomic or ionic mass of X. ∑ % value is lower than 100% indicating that the samples of the present study still contain some water after drying at 120˚C.

The results of the chemical and physical analysis (Table 2) allow us to calculate the number of each ion X per unit cell, n_x according to the following equation:

(2)

The results of these calculations are summarized in Table 3. The errors in Table 4 are estimated by the means of error propagation theory.

Table 2. Chemical Composition (weight percent) and Total Mass Balance ∑ % of the hydroxyapatites obtained by precipitation in solutions containing C_c (M) CO₃ and C_Mg (mM) Mg.

Table 3. Unit cell compositions of NaCO₃ Aaps calculated on the basis of the chemical composition and using Equation (2).

(a) (b) (c)

Table 4. Multiple linear regression analysis of Y_i = /n_P the molar ratio (Table 3) as a function of the concentration of carbonate C_c/M and magnesium C_Mg/mM in the solution. (a) Regression statistic; (b) Coefficients; (c) Analysis of variance.

4. Statistical Analysis of the Physicochemical Results

4.1. Influence of the Experimental Conditions on the Composition of the Synthetic Apatites

To know the influence of the experimental conditions on the incorporation of and Mg²⁺ in the lattice of these synthetic apatites, we graph Y_i = /n_P and n_Mg/n_P the molar ratios contents of the samples against X_i the concentration of C_c or the concentration of Mg²⁺ C_Mg in the solution, Figure 3 and Figure 4.

From the Figure 3(a) and Figure 4(a), it is seen that /n_P the molar ratio increases with the increase of the concentration of in the solution (C_c/M). Contrariwise, it varies slightly with the concentration of the Mg²⁺ ions in the solution and vice versa for n_Mg/n_P (Figure 3(b) and Figure 4(b)).

To estimate the simultaneous influence of the experimental conditions on /n_P and n_Mg/n_P the molar ratios, we construct a mathematical model of Y_i = /n_P or n_Mg/n_P on two variables X_1,i = C_c and X_2,i = C_Mg.

The mathematical model is described by the equation:

(3)

The method of least squares (O.L.S.) allows us to establish the predicted equation

(4)

that is most suitable to the data. On the other hand, this method allows us to calculate the estimated standard errors of the coefficients, the individual confidence interval at 95% level, R² the standardized statistic and to test the null hypothesis H₀: b_j = 0 and its significances level. The analysis of the variance for the linear regression or the F test allows us to ensure that at least one of the X-variables contributes to the regression. The theoretical basis of these calculations is given in references [32] -[34] . The calculations are summarized in Table 4 and Table 5.

4.2. Influence of the Incorporation of and Mg²⁺ on the Variation of Ca²⁺ and OH⁻ the Molar Ions Contents of the Synthetic Apatites

In attempts to disentangle and to measure the effects of the insertion of and Mg²⁺ ions on the molar con-

(a) (b)

Figure 3. (a) /n_P molar ratio of the solid versus C_Mg/mM for the samples prepared at different C_c/M; (b) n_Mg/n_P molar ratio of the solid versus C_Mg/mM for the samples prepared at different C_c/M.

(a) (b)

Figure 4. (a) /n_P molar ratio versus C_c/M for the samples prepared at different C_Mg/mM; (b) n_Mg/n_P molar ratio versus C_c/M for the samples prepared at different C_Mg/mM.

(a) (b) (c)

Table 5. Multiple linear regression analysis of Y_i = n_Mg/n_P molar ratio (Table 3) as a function of the concentration of carbonate C_c/M and magnesium C_Mg/mM in the solution. (a) Regression statistic; (b) Coefficients; (c) Analysis of variance.

tent of Ca²⁺ of the solid, we use the multiple linear regression on two X-variables where, X₁ = and X₂ = nMg²⁺ and Y is the estimate molar content of Ca²⁺ or OH⁻ (data Table 3). The results of these calculations are given in Table 6 and Table 7.

(a) (b) (c)

Table 6. Multiple linear regression analysis of the estimated Yi = nCa²⁺ on X_1,i = nMg²⁺, X_2,i = calcium, carbonate and magnesium respectively molar contents of the solid “B” Mg-CO₃ Haps. (a) Regression statistic; (c) Coefficients; (c) Analysis of variance.

(a) (b) (c)

Table 7. Multiple linear regression analysis of the estimated Y_i = OH⁻ on X_{1, i} = nMg²⁺ and X_2,i = the molar contents of the solid “B” Mg-CO₃ Haps. (a) Regression statistic; (b) Coefficients; (c) Analysis of variance.

4.3. The Determination of the Relationship between Y = c/a Crystallographic Parameters Ratio and / the Molar Ratio

To estimate the influence of the incorporation of carbonate on the lattice parameters “a” and “c” in presence of magnesium, we plot c/a crystallographic parameters ratio (Table 1) as a function of molar ratio /n_P (Table 3) for 0 ≤ n_Mg ≤ 17.4 mM (Figure 5).

Given that the shape of the curve obtained in Figure 5 is a polynomial, we construct a multiple linear regression on Y_i = c/a as a function of three X-variables where, X₁ = /n_P, X₂ = (/n_P)² and X₃ = (/n_P)³ (data Table 2) and Y is the estimate ratio of the hexagonal lattice dimensions (data Table 1). The mathematical model equation is

(5)

Least square [33] allows calculating the regression and correlation coefficients regression of the predicted

equation

(6)

These estimated rgression coefficients are calculated from the values of correlation coeffici- ents, variance and covariance according to the method of Scherrer [33] . This method allows us to test the utility of the model or the F-test according to:

(7)

where n is sample size, m is number of parameters and (n − m − 1) is degree of freedom.

On the other hand, this method allows us to calculate the standard errors of the coefficients and to conduct t-tests on the b’s (to discover which variable(s) is related to estimate) and to calculate the individual confidence interval at 95% level. The results of these calculations are given in Table 8.

The analysis of variance (ANOVA) shows that F-test = 2018.9 is higher than criterion F(5%; 3; 8) = 4.07.

(a) (b)

Table 8. Multiple linear regression analysis of Y_i= c/a ratio of the lattice parameters of Mg-CO₃ HAps (Table 1) on: X_1i = /n_P, X_2i = (/n_P)², X_3i = (/n_P)³ the molar ratio Table 3. (a) Statistic regression; (b) Coefficients.

Figure 5. c/a parameters ratio as a function of /n_P the molar ratio for the apatites prepared at different values of C_Mg.

5. Determination of the General Formula of the Unit Cell of the Synthetic “B” CO₃Mg-HAps

The relative composition (Table 3) and the results of the physical analysis demonstrate that the samples are pure “B” type carbonated apatites containing Mg²⁺ ions. Thus, mechanisms I, II, III and V could be account in the incorporation of on and Mg²⁺ ions are incorporated in the apatite lattice according to mechanisms III and/ or IV.

Moreover, the study carried out previously (paragraph 4.1) show that the ions are incorporated in the apatite lattice independently of the concentration of Mg²⁺ ions solution. This result confirms that mechanism IV does and mechanism III does not contribute to the incorporation of Mg²⁺ in the apatites.

Many works [27] [28] have demonstrated that mechanism I and/or II are the main mechanisms for the incorporation of CO₃. Otherwise, according the reference [27] , the contribution of mechanism I seems to be hardly influenced by the alkali metal which is not our case. Therefore, we consider that mechanism II contribute to the insertion of CO₃ ions in the lattice of the solid.

Table 7 show that the variation of nOH⁻ depends on the increase of and Mg²⁺. So, it may be said in the present study, that the mechanism V could account.

Then the fundamental substitution mechanisms for the incorporation of and Mg²⁺ in the HAp lattice are:

(II)

2.(IV)

(V)

where V^OH stands for a vacancy in the OH⁻ sub lattice. If x, y and z are the contributions of mechanisms II, 2.IV and V respectively, thus,

(8)

(9)

(10)

(11)

and (12)

and the generic formula has the following expression:

The values of x, y and z the contribution of mechanisms II, 2.IV and V respectively are calculated from the data (Table 3) and the following equations. Then statistical studies are conducted to verify the accuracy of the proposed formula. The results of these calculations are summarized in Tables 9-11.

Table 9. The values of x, y and z the contributions of the mechanisms II, 2.IV and V respectively calculated from Equations (10)-(14).

(a) (b) (c)

Table 10. Multiple linear regression analysis of the estimated Y_i = nCa²⁺ the molar content of the solid “B” Mg-CO₃ HAps (Table 3) on X_1,i = x- and X_2,i = y the contribution of mechanisms II and 2.IV (Table 9). (a) Regression statistic; (b) Coefficients; (c) Analysis of variance.

(a) (b) (c)

Table 11. Multiple linear regression analysis of the estimated Y_i = nOH⁻ the molar content of the solid “B” Mg-CO₃ HAps (Table 3) on X_1,i = z and X_2,i = z the contribution of mechanisms II and V (Table 9). (a) Regression statistic; (b) Coefficients; (c) Analysis of variance.

6. Discussion

From Table 1,, we can see that simultaneous incorporation of two elements “CO₃ and Mg” results in an decrease of the “a” parameter. This contraction is attributed to the simultaneous effects of the and Mg²⁺ substitutions [4] .

In Table 2 and Table 3, it is seen that the concentration of the ions in the solution C_c does not affect the quantities of Mg²⁺ ions inserted in the solid. Because, regardless ofthe concentration of the ions in the solution C_c, the Mg²⁺ ions contents of the samples increase proportionally with the increase of the concentration of Mg²⁺ ions in solution C_Mg. This result is in agreement with reference [4] . For the same concentration of Mg²⁺ions in the solution C_Mg, the variation of and contents of the solid do not seem to be correlated with the concentration of the Mg²⁺ ions in the solution, while the Ca²⁺content depends on the concentrations of C_c and Mg²⁺ C_Mg in the solution.

Figure 3 and Figure 4, show that nCO₃/nP the molar ratio increases with the increasing of the concentration of in solution (C_c/M). Contrariwise, it varies slightly with the concentration of Mg²⁺ ions in solution and vice versa for nMg/nP. The statistical treatment of the experimental data Table 4 and Table 5 allows us to establish the estimated equations between these variables at 95% levels

(13)

and (14)

Equations (9) and (10) show that the concentration of the ions in the hydrolysis solution C_c affects the quantities of and Mg²⁺ ions incorporated in the solid, but the concentration of Mg²⁺ ions in solution C_Mg does not affects the quantities of ions in the solid. These results are in agreement with those found in the reference [27] .

To know the relationship between the variation of Ca²⁺ and OH⁻ with the increasing of and Mg²⁺ content in the solid, statistical studies are conducted. The results of multiple linear regression Table 6 and Table 7 show that the estimated equations on these variables are represented at 95% level by:

(15)

(16)

From the intercepts of the following equations it can seen that, within experimental error, a carbonate and magnesium-free apatite (nCO₃ = 0, nMg = 0) contains 10 Ca²⁺ and 2 OH⁻ ions per unit cell Equations (11) and (12). These results are in agreement with those in literature [24] - [26] [34] [35] .

As shown in Figure 5, there is a correlation of the unit cell parameters of the apatites with their chemical compositions. Indeed, the changes in the unit cell parameter “a” of the compounds are attributed to the additive effects of the substitution in the lattice of either carbonate and magnesium [2] [34] [35] . The solid line of best fit for these series of compounds in Figure 5 extrapolates to a ratio c/a very close to that in hydroxyapatite. This result is similary to these obtained previously [34] [35] . The application of multiple linear regression to Y_i = c/a

on allows us to establish the predicted equation at

95% level:

(17)

To verify the general formula proposed, We apply the multiple linear regression to Yi = nCa²⁺ on X_1i = x and X_2i = y (the contributions of the mechanisms II and IV). Similar treatment is realized for Yi = nOH⁻ on X_1i = z and X_2i = y (the contributions of the mechanisms V and IV) Table 10 and Table 11. The results of these calculations show that the predicted equations at 95% level are:

(18)

(19)

7. Conclusion

The theoretical calculations of the present study indicate unambiguously that the mechanisms II, III and V contribute to the incorporation of Mg and Ca in the lattice of apatite. This corroborates in more definite way our assumptions obtained from the experimental data and allows us to propose for these compounds the general formula:

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Kreidler, E.R. and Hummel, F.A. (1970) The Crystal Chemistry of Apatite: Structure: Fields of Fluor- and Chlorapatite. American Mineralogist, 55, 170.
[2]	Legeros, R.Z. (1984) Tooth Enamel IV. In: Fearnhead, R.W. and Sugas, S., Eds., Elsevier, Amsterdam, 32-36.
[3]	Ben Abdelkader, S., Khattech, I., Rey, C. and Jemal, M. (2001) Synthése, Caractérisation et Thermochimie d’Apatites Calco-Magnésiennes Hydroxylées et Fluorées. Thermochimica Acta, 376, 25-36. http://dx.doi.org/10.1016/S0040-6031(01)00565-2
[4]	Terpstra, R.A. and Driessens, F.C.M. (1986) Magnesium in Tooth Enamel and Synthetic Apatites. Calcified Tissue International, 39, 348-354. http://dx.doi.org/10.1007/BF02555203
[5]	Hayek, E. and Newsely, H. (1958) über die Existenz von Tricalciumphosphat in waBriger Losung. Mn. Chem., 89, 88.
[6]	Rowles, S.L. (1968) Crystallographic Study of Biological Apatites. Bulletin de la Société Chimique de France, 1797.
[7]	Hamad, M. and Heughebaert, J.C. (1987) Study of Apatite and Whitlockite Formation at 100°C in the System CaO-MgO-P2O5-H2O. J. Chim. Phys., 84, 985.
[8]	Vignoles, M., Bonel, G. and Young, R.A. (1987) Occurrence of Nitrogenous Species in Precipitated B-Type Carbonated Hydroxyapatites. Calcified Tissue International, 40, 64-70. http://dx.doi.org/10.1007/BF02555707
[9]	Vignoles, M., Bonel, G., Holcomb, D.W. and Young, R.A. (1988) Influence of Preparation Conditions on the Composition of Type B Carbonated Hydroxyapatite and on the Localization of the Carbonate Ions. Calcified Tissue International, 43, 33.
[10]	Young, R.A. and Spooner, S. (1969) Neutron Diffraction Studies of Human Tooth Enamel. Archives of Oral Biology, 15, 47-63. http://dx.doi.org/10.1016/0003-9969(70)90144-5
[11]	Bigi, A., Foresti, E., Gregorini, R., Ripamonti, A., Roveri, N. and Shah, J.S. (1992) The Role of Magnesium on the Structure of Biological Apatites. Calcified Tissue International, 50, 439-444. http://dx.doi.org/10.1007/BF00296775
[12]	Holden, J.L., Clement, J.G. and Phakey, P.P. (1995) Age and Temperature Related Changes to the Ultrastructure and Composition of Human Bone Mineral. Journal of Bone and Mineral Research, 10, 1400-1409. http://dx.doi.org/10.1002/jbmr.5650100918
[13]	Robinson, C., Weatherell, J.A. and Hallsworth, A.S. (1981) Distribution of Magnesium in Mature Human Enamel. Caries Research, 15, 70-77. http://dx.doi.org/10.1159/000260502
[14]	Steinfort, J., Driessens, F.C.M., Heijligers, H.J.M. and Bertseen, W. (1991) The Distribution of Magnesium in Developing Rat Incisor Dentin. Journal of Dental Research, 70, 187-191. http://dx.doi.org/10.1177/00220345910700030601
[15]	Tsuboi, S., Nakagi, H., Ishiguro, K., Kondo, K., Mukai, M., Robinson, C. and Weatherell, J.A. (1994) Magnesium Distribution in Human Bone. Calcified Tissue International, 54, 34-37. http://dx.doi.org/10.1007/BF00316287
[16]	Bigi, A., Marchetti, F., Ripamonti, A., Roveri, N. and Foresti, E. (1981) Magnesium and Strontium Interaction with Carbonate-Containing Hydroxyapatite in Aqueous Medium. Journal of Inorganic Biochemistry, 15, 317-327. http://dx.doi.org/10.1016/S0162-0134(00)80235-4
[17]	Featherstone, J.D.B., Mayer, I., Driessens, F.C.M., Verbeeck, R.M.H. and Heijligers, H.J. (1983) Synthetic Apatites Containing Na, Mg, and CO3 and Their Comparison with Tooth Enamel Mineral. Calcified Tissue International, 35, 169-171. http://dx.doi.org/10.1007/BF02405026
[18]	Apfelbaum, F., Mayer, I. and Featherstone, J.D.B. (1991) The Role of HPO2-4 and CO2-3 Ions in the Transformation of Synthetic Apatites to β-Ca3(PO4)2. Journal of Inorganic Biochemistry, 38, 1-8. http://dx.doi.org/10.1016/0162-0134(90)85001-D
[19]	Aoba, T., Moreno, E.C. and Shimoda, S. (1992) Competitive Adsorption of Magnesium and Calcium Ions onto Synthetic and Biological Apatites. Calcified Tissue International, 51, 143-150. http://dx.doi.org/10.1007/BF00298503
[20]	Okazaki, M. and Legeros, R.Z. (1992) Crystallographic and Chemical Properties of Mg-Containing Apatites before and after Suspension in Solutions. Magnesium Research, 5, 103-108.
[21]	Zhou, J.M., Zhang, X.D., Chen, J.Y., Zeng, S.X. and De Groot, K. (1993) High Temperature Characteristics of Synthetic Hydroxyapatite. Journal of Materials Science: Materials in Medicine, 4, 83-85. http://dx.doi.org/10.1007/BF00122983
[22]	Legeros, R.Z., Kijkowska, R., Bautista, C. and Legeros, J.P. (1995) Synergistic Effects of Magnesium and Carbonate on Properties of Biological and Synthetic Apatites. Connective Tissue Research, 333, 203.
[23]	Mayer, I., Schlam, R. and Featherstone, J.D.B. (1997) Magnesium-Containing Carbonate Apatites. Journal of Inorganic Biochemistry, 66, 1-6. http://dx.doi.org/10.1016/S0162-0134(96)00145-6
[24]	Gibson, I.R. and Bonfield, W. (2002) Preparation and Characterization of Magnesium/Carbonate Co-Substituted Hydroxyapatites. Journal of Materials Science: Materials in Medicine, 13, 685-693. http://dx.doi.org/10.1023/A:1015793927364
[25]	Baravell, S.S., Bigi, A., Ripamonti, A., Roveri, N. and Foresti, E. (1984) Thermal Behavior of Bone and Synthetic Hydroxyapatites Submitted to Magnesium Interaction in Aqueous Medium. Journal of Inorganic Biochemistry, 20, 1-12. http://dx.doi.org/10.1016/0162-0134(84)80001-X
[26]	De Maeyer, E.A.P. and Verbeeck, R.M.H. (1993) Possible Substitution Mechanisms for Sodium and Carbonate in Calciumhydroxyapatite. Bulletin des Sociétés Chimiques Belges, 102, 601-609. http://dx.doi.org/10.1002/bscb.19931020907
[27]	De Maeyer, E.A.P., Verbeeck, R.M.H. and Pieters, I.Y. (1996) Influence of the Solution Composition on the Stoichiometry of Na+- and of K+-Containing Carbonated Apatites Obtained by the Hydrolysis of Monetite. Journal of Crystal Growth, 169, 539-547. http://dx.doi.org/10.1016/S0022-0248(96)00424-1
[28]	De Maeyer, E.A.P., Verbeeck, R.M.H. and Pieters, I.Y. (1996) Effect of K+ on the Stoichiometry of Carbonated Hydroxyapatite Obtained by the Hydrolysis of Monetite. Inorganic Chemistry, 35, 857-863. http://dx.doi.org/10.1021/ic950916k
[29]	Charlot, G. (1966) Les Méthodes de la Chimie Analytique. Masson, Paris.
[30]	Gee, A. and Deitz, V.R. (1953) Determination of Phosphate by Differential Spectrophotometry. Analytical Chemistry, 25, 1320-1324. http://dx.doi.org/10.1021/ac60081a006
[31]	Legeros, R.Z. (1991) Calcium Phosphates in Oral Biology and Medicine. Monographs in Oral Science, 15, 89-95.
[32]	Snedecor, G.W. and Cochran, W.G. (1980) Statistical Methods. 7th Edition, The Iowa State University Press, Ames.
[33]	Borcard, D. (2009) Regression Multiple. Université de Montréal, Montréal. http://biol09.biol.umontreal.ca/BIO2042/Regr_mult.pdf
[34]	Bel Hadj Yahia, F. and Jemal, M. (2010) Synthesis, Structural Analysis and Thermochemistry of B-Type Carbonate Apatites. Thermochimica Acta, 505, 22-32. http://dx.doi.org/10.1016/j.tca.2010.03.017
[35]	Rockh B. Hadj Yahia, F. and Khattech, I. (2014) Statistical Studies of the Physicochemical Analytic Results of a Series of Synthetic Calcium Hydroxyapatite Containing Carbonate and Sodium. American Journal of Analytical Chemistry, 5, 343-357.