A Nonparametric Derivative-Based Method for R Wave Detection in ECG ()
1. Introduction
QRS wave is the most visible part of the changes in the ECG (electrocardiogram) and the synthetic performance of the multi-myocardial cells. So detecting QRS wave accurately not only provides important basis for the diagnosis of arrhythmia, but also makes it possible to count the heart rate and the variability of heart rate in this base. By doing so, it can lay the foundation for further detecting and analyzing other detailed information. So the key is to detect reliable QRS wave in the analysis of ECG signals accurately.
However QRS waves are difficult to be detected; not only are there the physiological variability of the QRS waves but also several various types of noises that would present in ECG signals. The main several noises sources include muscle noises, artifacts due to electrode motion, 50 Hz power frequency interference, and baseline wander. Therefore we use a digital filter to cut out noises from the original ECG signals before detecting R wave in this paper, and select appropriate thresholds by the difference to deal with the data smoothly. Thus we can obtain more stable signals to prepare for the further R wave detection.
The QRS waves detection of ECG signals have been researched for many years. There have been mainly several investigations dealing with the QRS wave detection for ECG signals [1] -[5] . For instance, difference thresholds method [6] -[10] can effectively reduce low frequency interference and it is easier to be implemented. Wavelet transform method [11] -[16] has good time frequency localization characteristics and high adaptability to time-varying signals. But it computes tediously and costs long time and it is not conducive to the timely processing. Filter bank method [17] -[19] is based on wavelet transform, while its implementation is more flexible and has higher accuracy than wavelet transform. Geometrical matching approach [20] -[21] has strong anti- interference but computes a lot of time. Neural network approach [22] -[25] has a strong adaptability and good discriminant results, but the training takes a long time. The algorithm of mathematical morphology [26] -[29] can effectively protrude the peaks and valleys of the signal by using the local characteristics of signal. The QRS waves can be eliminated by a series of morphological operations. Then the start points and the end points of P2 wave and T2 wave can be decided and the waves of ECG are separated qualitatively and quantitatively. The above approaches have advantages and disadvantages. Meanwhile they have their own ranges of adaption. Because the adaptive difference threshold algorithm is easy to be implemented, this paper still uses difference threshold algorithm to select thresholds and self-learning strategies are used to compute thresholds. A non-parametric derivative-based method was proposed for the detection of R wave in ECG with local polynomial regression which is used in many fields [30] -[39] . Finally, clinical experimental data is used to evaluate the effectiveness of the algorithm. Experimental results show that the method in the process of the detection of R wave is much smoother, comparing with difference threshold algorithm, and it can detect the R wave in the ECG accurately.
The rest of the paper is organized following. R wave detection with local polynomial regression and its derivative’s estimation is depicted in Section 2. Experiments results and discussions are given in Section 3. Conclusions are obtained in Section 4.
2. R Wave Detection with Local Polynomial Nonparametric Regression
After the original ECG signal data is preprocessed, we use the local polynomial nonparametric statistical regression to fit these data and compute its values of first-order derivative which can be applied in the algorithm of R- wave detector in ECG signal. In view of these values of first-order derivative, we find they have relatively large changes; there is a fixed position relationship with the steep waveform R wave. Firstly, we set three initial thresholds, comparing with derivative values based on the local polynomial nonparametric estimation. Then through the adaptive learning to adjust the size of thresholds, thus derivative values that can meet the threshold conditions are able to determine the location of R wave roughly. Last setting different RR intervals to discuss redundancies and lacks of R wave and fix.
2.1. Preprocessing Data and ECG Signal De-Noise
Since it is difficult to detect QRS wave complexes. Not only because of the physiological variability of the QRS complexes, but also the various types of noises that can present in ECG signals. The main several noises sources include artifacts due to electrode motion, power-line interference, baseline wander. Therefore the first thing is to preprocess data and signals filtering before detecting ECG signals in this paper. The work is divided into the following three steps to complete:
1) Because the data most front excess zeros is meaningless, we process the data in front of extra zeroes method is using a threshold to judge. The method is that from the first point that its absolute value is greater than this threshold to start account, the following data as the signals data to be processed.
2) Data judgment: first, expand the amplitude of the signals up to 100 times of the original (For convenience of signal-detection, the amplitude does not have to be expanded.). Take the first two seconds signals data to identify the position of one of the largest difference, there must be a QRS wave before or after the largest difference value. Finding the maximum pre-max and minimum pre-min value within the interval [−fs/8 fs/8] before and after the origin (fs is sample rate). Meanwhile based on the interval value ranking, we choose its mean value pre-mid. According to distance between the maximum, minimum and mean value to judge whether the signals data is positive or negative and adjust signals.
3) In the process of ECG signals acquisition, amplification and transformation, it can cause all kinds of interference. The main interference is 50 Hz power frequency interference and baseline wander. We use a multi band-pass digital filter to smooth signals after A/D converted. The filter is a 280-order FIR digital filter design with rectangular window. Based on difference of sampling rate, the choice of band-pass has lightly changes. When sampling frequency fs = 5000, the band-pass W = [5.5 40 60 90 110 140 160 190]/fs*2, other smaller fs, W = [5.5 48 52 98 102 148 152 198]/fs*2. It is verified that this multi band-pass rectangular window can filter most of 50 Hz and some harmonic power frequency interference and baseline wander.
The original ECG signal is plotted in Figure 1. Figure 1 shows the original ECG heart rate is relatively stable. That is, the interference is so small that we can use multi band-pass digital filter to cut out noises from the original ECG signals easily.
2.2. Thresholds Setting and RR Interval
After the original ECG signal data is preprocessed, the first 500 samples would be divided equally. Then we make T = round (1.1*RR) and calculate the difference maximum of the first five T. After removing a maximum and a minimum, the remaining values are taken arithmetic average to obtain threshold benchmark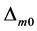 . We set
. We set
three constants 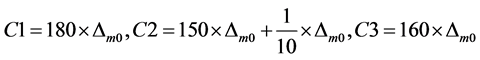 through
through , and use initial benchmark determine
, and use initial benchmark determine , which is the threshold for preparing R de-
, which is the threshold for preparing R de-
tection, according to three cycles to adjust thresholds in the adaptive phase. We also need obtain benchmark R wave amplitude HR and benchmark R wave interval RR: first taking the first 12 seconds signals preprocess to find the maximum difference, next using the maximum difference of 0.65 times as the threshold, we could obtain a general RR interval that we set h. Then we compute the maximum difference and the maximum amplitude value and its corresponding position. We obtain RR interval and space HR.
2.3. Local Polynomial Nonparametric Regression of ECG Data
1) Local polynomial fitting
For data set  in each period, where
in each period, where  is the response and
is the response and  is time variable. One may fit a regression curve
is time variable. One may fit a regression curve 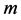 through the data to establish the relationship between the response and time variable. Discrepancies between the regression curve and the data are usually treated as noise. Therefore, we have the model:
through the data to establish the relationship between the response and time variable. Discrepancies between the regression curve and the data are usually treated as noise. Therefore, we have the model:
 (1)
(1)
where 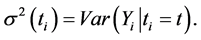 Often one can assume that
Often one can assume that ,
, 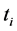 and
and 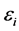 are mutually independent. Let
are mutually independent. Let  be the
be the  -th derivative of the regression function defined in (1). The local polynomial technique is very convenient to use for estimating
-th derivative of the regression function defined in (1). The local polynomial technique is very convenient to use for estimating![]() , including the regression function itself
, including the regression function itself ![]() and its the first-order derivative functions
and its the first-order derivative functions![]() . Since the form of the function
. Since the form of the function ![]() is
is
not specified, a remote data point from ![]() provides very little information about
provides very little information about![]() . Hence, we can only use the local data points around
. Hence, we can only use the local data points around![]() . Assume that
. Assume that ![]() has the (p + 1) derivative at the point
has the (p + 1) derivative at the point![]() . By Taylor expansion, for
. By Taylor expansion, for ![]() in the local neighborhood of
in the local neighborhood of![]() , we have:
, we have:
![]() (2)
(2)
In terms of statistical modeling, locally around![]() , we model
, we model ![]() as
as
![]() (3)
(3)
The parameters ![]() depend on
depend on ![]() and are called local parameters. Clearly, the local parameter
and are called local parameters. Clearly, the local parameter ![]()
Fitting the local model (3) using the local data, one minimizes
![]() (4)
(4)
where ![]() is a bandwidth controlling the size of the local neighborhood and
is a bandwidth controlling the size of the local neighborhood and ![]() is a kernel function. In this paper, after many experiments that we choose the bandwidth
is a kernel function. In this paper, after many experiments that we choose the bandwidth![]() , kernel function is
, kernel function is
![]() . Let:
. Let:
![]()
![]() (5)
(5)
Then the problem of weighted least squares estimation can be written as follows:
![]() (6)
(6)
where![]() . The i-th element of W is
. The i-th element of W is![]() , its solution vector is:
, its solution vector is:
![]() (7)
(7)
where![]() ,
,![]() .
.
For the nonparametric local polynomial estimator, there are three important problems which have significant influence to the estimation accuracy and computational complexity.
First of all, there is the choice of the bandwidth, which plays a rather crucial role. The most important thing is to find the bandwidth. In theory, there exists a optimal bandwidth ![]() in the meaning of mean integrated square error (MISE), fulfilling the equality
in the meaning of mean integrated square error (MISE), fulfilling the equality
![]() (8)
(8)
However, the theoretical bandwidth ![]() in Formula (8) can not be directly calculated. Here, we apply a search method to select the bandwidth: Compare values of the objective function as the bandwidth
in Formula (8) can not be directly calculated. Here, we apply a search method to select the bandwidth: Compare values of the objective function as the bandwidth ![]() from small to large, and then find out the optimal bandwidth which minimizes the objective function.
from small to large, and then find out the optimal bandwidth which minimizes the objective function.
Suppose that ![]() where
where ![]() is the minimum,
is the minimum, ![]() is coefficient of expansion. We search a bandwidth
is coefficient of expansion. We search a bandwidth ![]() to minimize the objective function in the interval
to minimize the objective function in the interval![]() , where the objective function refers to the prediction mean square error (MSE), denoted by
, where the objective function refers to the prediction mean square error (MSE), denoted by![]() .
.
Firstly, we assume![]() , then increase
, then increase ![]() by efficient of expansion
by efficient of expansion ![]() and calculate value of objective function for each
and calculate value of objective function for each![]() . Stop down when
. Stop down when![]() , and choose a bandwidth
, and choose a bandwidth ![]() which minimizes
which minimizes ![]() as the
as the
approximate optimal bandwidth. ![]() can be taken place by a estimation
can be taken place by a estimation![]()
In this paper, we choose
![]() (9)
(9)
where ![]() Compared with other methods, this method is more convenient.
Compared with other methods, this method is more convenient.
In order to closer to the ideal optimal bandwidth, we search once again by narrowing the interval on the basis of the above searching process. Supposing ![]() is the bandwidth which make
is the bandwidth which make ![]() optimal in the above sear-
optimal in the above sear-
ching process. Now, divide the small interval ![]() into
into ![]() equal intervals. Supposing
equal intervals. Supposing
![]() (10)
(10)
among these ![]() bandwidths, the approximate optimal bandwidth is the one that makes
bandwidths, the approximate optimal bandwidth is the one that makes ![]() minimize. Obviously, this search method can quickly select the right bandwidth.
minimize. Obviously, this search method can quickly select the right bandwidth.
Another issue in multivariate local polynomial fitting is the choice of the order of the polynomial. For a given bandwidth![]() , a large value of
, a large value of ![]() would expectedly reduce the modeling bias, but would cause a large variance and a considerable computational cost. Since the bandwidth is used to control the modeling complexity, and due to the sparsity of local data in multi-dimensional space, a higher-order polynomial is rarely used. So we apply the local quadratic regression to fit the model (that is to say,
would expectedly reduce the modeling bias, but would cause a large variance and a considerable computational cost. Since the bandwidth is used to control the modeling complexity, and due to the sparsity of local data in multi-dimensional space, a higher-order polynomial is rarely used. So we apply the local quadratic regression to fit the model (that is to say,![]() ).
).
The third issue is the selection of the kernel function. In this paper, we choose the spherical Epanechnikov kernel as kernel function
![]() (11)
(11)
where ![]() represents
represents ![]() function. This is the optimal kernel function.
function. This is the optimal kernel function.
500 data are contained in a cycle in Figure 2. The samples number of data which is used in local polynomial nonparametric statistical method is 500. This is as same as original data. Compared with original signals, the first-order derivatives which we estimate have fixed position with it. There must be R peak between the maximum and minimum of the first-order derivative. Thus we can choose appropriate thresholds to limit first-order derivative values range so that the position of R wave can be determined approximately.
2) Algorithm of R wave detection
We put![]() , any of the three estimated values in each period are
, any of the three estimated values in each period are![]() ,
, ![]() ,
, ![]() , if
, if
![]() (12)
(12)
we can determine ![]() is an R wave. The Figure 3 is generally detection of R wave flow chart, which
is an R wave. The Figure 3 is generally detection of R wave flow chart, which
![]()
Figure 2. Results of fitting with local polynomial nonparametric regression.
give the detailed description for the R detection of ECG signal. Firstly, the local polynomial nonparametric regression is applied to fitting and estimate the ECG signal. Then, the initial thresholds are given. Finally, iterations steps are conducted for the R wave detection.
2.4. Check and Correction for R Wave in ECG Signal
Firstly, we need to judge whether it is a real QRS wave when an R wave is detected. We determine the redundant detection occurs according to whether the current RR interval is larger than 0.8*RR or not. Then we decide the missing detection occurs according to whether the RR is more than 3.1*RR or not. If redundant detection or missing detection occurs, we need detect the sample paragraph again before the current sample paragraph be detected and increase range in order to detect the R wave conveniently.
It is possible that the judgment includes redundant detection or missing detection though we have done above. Therefore we also need further determine whether RR is in the interval between 1.66*RR and 2.5*RR. If it is in this interval, it shows that it is possible to be a missing R wave.
From Figure 4, our solution is as follows: we should judge whether the signal in [0.5*HR, 1.5*HR] lies in [0.7*RR, 1.2*RR]. If it occurs, we can draw a conclusion that an R wave is missed. Then we supplement it to the sequence of the R wave position. If it can not occur, we should check whether an invert R wave exists. If it exists, we should supplement it to above sequence. If the testing program runs to the last data and finds that the distance between the position of the last R wave and the end of the data exceeds 1.66*RR, we detect the last part of the signals once more.
From Figure 5, the algorithm is summarized as follows:
![]()
Figure 4. Fix check detection redundancies.
Step 1: Using the given threshold to removal the data most front excess zeros, and the finding difference of maximum and minimum values to judge the data.
Step 2: Choosing a multi band-pass digital filter to filter and smooth signals after A/D converted.
Step 3: Calculating thresholds and obtaining the RR intervals by the difference method.
Step 4: Using local polynomial fitting to process data and obtain the values of its first-order derivative.
Step 5: By fourth step calculated first-order derivative values, combined with thresholds, we can detect the a- pproximate location of R wave by satisfying the three conditions (Formula 7).
Step 6: Setting different RR intervals and discussing redundancies and missing R wave and correcting it.
3. Experiment Results and Discussions
The purpose of by using local polynomial nonparametric fitting modeling process in R wave detection of ECG signal is to obtain the values of its first-order derivative of the original ECG data in each point. For smaller calculation of the proposed approach, we determine the order ![]() for the local polynomial in the fitting process. In addition, there are two parameters of the model which must be selected in some sense of optimization. The one is the size of the bandwidth
for the local polynomial in the fitting process. In addition, there are two parameters of the model which must be selected in some sense of optimization. The one is the size of the bandwidth![]() , the other is choice of kernel function in local polynomial nonparametric estimation process. In this paper, we choose the bandwidth
, the other is choice of kernel function in local polynomial nonparametric estimation process. In this paper, we choose the bandwidth ![]() is 0.005, by according to the optimal in mean square. Also because ECG data values are small, we should estimate all observations in a cycle. The difference between the observed values is 0.001. If the bandwidth is less than 0.005, it would result in under smooth, obtain noisy estimates, where if a bandwidth is too large, it would cause over smooth, and create excessive modeling bias. The bandwidth can be chosen subjectively by users by visually inspecting resulting estimates or chosen automatically by data by minimizing a depicted former theoretical approach. The order
is 0.005, by according to the optimal in mean square. Also because ECG data values are small, we should estimate all observations in a cycle. The difference between the observed values is 0.001. If the bandwidth is less than 0.005, it would result in under smooth, obtain noisy estimates, where if a bandwidth is too large, it would cause over smooth, and create excessive modeling bias. The bandwidth can be chosen subjectively by users by visually inspecting resulting estimates or chosen automatically by data by minimizing a depicted former theoretical approach. The order ![]() has been identified. The kernel function has been selected according to the optimal theory.
has been identified. The kernel function has been selected according to the optimal theory.
3.1. Feasibility Test
We choose ECG signals randomly to test the algorithm. We also choose 500 data in accordance with the above steps to detect the R wave in ECG signal. The Figure 6 is some results.
Figure 6 shows that the algorithm is feasible for R wave detection in regular ECG signals. The symbol * represents R peaks which have been detected. We can find easily R waves are detected exactly and wave peaks are marked. Thus we can judge whether this period of R intervals are equal consistent so that it can provide reference for the clinical ECG diagnosis.
3.2. R-Wave Detection with Local Polynomial Nonparametric Regression
In experiments we select 500 samples in a cycle as the optimal number of samples. Then we fit the original data using local polynomial nonparametric method in a period. The fitted data are all the same as data of the original data. So we can locate R wave position with its first derivative accurately. We adjust the size of the thresholds by the use of adaptive learning in order to complete the redundant detection and missing detection of the R wave successfully.
Experiments show that the method of local polynomial fitting can also smooth the original data during the progress of real-time detecting R wave. The method can detect R wave more accurately and stably, comparing with the difference threshold method.
The Figure 7 are the parts of the figures of the experimental result and the corresponding instantaneous heart rate chart that we get when we detect the R wave by using local polynomial fitting.
Because the QRS waves we detect are stable normal heart rate and we fit the original data by using local polynomial estimation, the instantaneous heart rate detection is almost in a straight line. The result shows that it is stable. We can also conclude that the algorithm detection is more accurate.
3.3. Comparing with the Differential Threshold Algorithm
Compared with the difference threshold algorithm, for our investigated nonparametric local polynomial method, the main difference is data preprocessing. The differential threshold algorithm is that ECG waveform amplitude which is calculated directly by the differential relative to the variation rate of time compared with the set threshold to meet the threshold condition is considered to be an R wave. The Figure 8 is the chart for the comparison.
![]()
Figure 6. The results of feasibility test.
![]()
Figure 7. Corresponding instantaneous heart rate chart.
![]()
Figure 8. Comparison of local polynomial fitting and differential threshold method.
It can be seen from Figure 8 in the signals amplitude of ECG after preprocessing. The effect of using local- polynomial fitting is smoother than the difference threshold method. Signals data obtained by the first method is better to maintain variations of the original signals data, especially in some of the inflection points at the fluctuation which are more accurate than the effect of the difference method. So in the use of adaptive threshold detection of R wave process, the data of using local polynomial fitting is even easier to detect the R wave accurately.
3.4. The Discussion of Redundant Detection and Missing Detection
When we obtain the position of the R wave, it is also necessary to discuss redundant detection and missing detection in ECG signal. The reason is that in the process of automatically updating thresholds, not all thresholds could satisfy rang of R wave peak. It is possible for some signals judged as R wave peak incorrectly in ECG signal so that we could not detect R wave accurately and efficiently. Therefore we could detect R wave and give corresponding correction accurately through researching redundant detection and missing detection.
From Figure 9 and Figure 10, the symbol * represents R wave peaks which have been detected. Obviously some not-R wave peaks also have been detected wrongly. It is not enough to depend on the size of thresholds to
![]()
Figure 9. The diagram before redundant detecting.
define range of R wave without making discussion of redundant detection. While after dealing with situation, some camouflage signals are detected. Then we set different RR intervals so that getting rid of these unnecessary signals. By doing so, the accuracy is improved greatly.
3.5. The Discussion of Redundant Detection and Missing Detection
When we obtain the position of the R wave, it is also necessary to discuss redundant detection and missing detection in ECG signal. The reason is that in the process of automatically updating thresholds, not all thresholds could satisfy rang of R wave peak. It is possible for some signals judged as R wave peak incorrectly in ECG signal so that we could not detect R wave accurately and efficiently. Therefore we could detect R wave and give corresponding correction accurately through researching redundant detection and missing detection.
4. Conclusion
In this paper we propose a non-parametric derivative-based method for R wave detection in ECG signal. After using a digital filter to cut out noises from noisy ECG signals, we utilize local polynomial nonparametric statistical regression to estimate the original signal and its derivative values, and then select appropriate thresholds by the difference. The algorithm automatically adjusts the size of thresholds periodically according to the different needs. Then the position of R wave is detected by the estimation of the values of the first-order derivatives which are obtained by using local polynomial nonparametric statistical fitting technique. In addition, the methods of redundant detection and missing detection are applied in this paper in order to improve the accuracy of detection. The clinical experimental data are used to evaluate the effectiveness of the algorithm based on derivatives of nonparametric statistical model. The results of the experiment show that using local polynomial fitting of original data in the algorithm can suppress some noises effectively and smooth the original data. At the same time, we can detect out the R wave timely and accurately. This is further improvement comparing with the former difference threshold method. However, heart rate variability can not be researched in this paper; it needs study further.
Acknowledgments
Project was supported by Natural Science Foundation Project of China (Grant No. 11471060), Fundamental and Advanced Research Project of CQ CSTC of China (Grant No. cstc2014jcyjA40003), and Natural Science Foun- dation Project of CQ CSTC of China (Grant No. CSTC2012jjA00037).