Macroscopic anisotropic Brownian motion is related to the directional movement of a “Universe field” ()
Although Einstein pointed out in 1905 that the bombardment by fast-moving atoms or molecules in a liquid or gas is the mechanism of Brownian motion [1], which is subsequently believed to be at least partially attributable to the thermal fluctuations of molecules [2-6], however, to date, the true origin of the Brownian motion has remained largely unexplained. In addition, there are debates concerning the origin of the irregularity that causes the stochastic, random character of Brownian trajectories [7], and it also turns out that not all features of the microscopic inputs of Brownian motion contribute to the macroscopic observable phenomena, such as the ubiquitous fluctuations of extended systems in natural and social science [8].
Microscopic observation of the Brownian motion of a single (round or ellipsoidal) particle interacting with its environment has demonstrated that short-term diffusive Brownian motion is an anisotropic process (ballistic diffusion), while the long-term diffusion is an isotropic process, which is believed to be completely random and obeys the Gaussian distribution [9-11]. Therefore, it can be assumed that the macroscopic diffusion regime of a group of particles such as a very small amount of colloid solution suspended in a liquid should theoretically be isotropic (symmetric) in a relatively long-term diffusion process when the influence of gravity is neglected, which means that the particles of this colloid solution should diffuse equally in every direction in two dimensions because of the concentration gradient effect (steady-state diffusion, Fick’s first law) and Brownian motion. Here, an experimental method was designed to observe the macroscopic diffusion regime of a toluidine blue colloid solution in water in a relatively long-term process (40 min) at different time points of the earth’s spin and revolution. Unexpectedly, an anisotropic (asymmetric) diffusion regime that presented circadian and seasonal changes was identified, which may prove to be an effect of the directional movement of the “Universe field” proposed by a recent theoretical model [12], and provide an in-depth explanation for the origin of Brownian motion.
2. METHODS
A schematic representation of the experimental method is shown in Figure 1. A black square container (37 cm
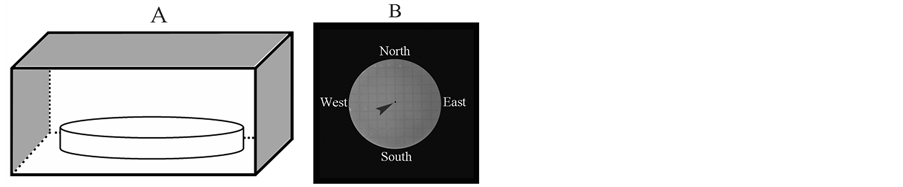
Figure 1. Schematic showing the test of the long-term anisotropic (asymmetric) Brownian diffusion of a toluidine blue colloid solution in water. (A) Front-back view of the instrument. (B) Top-down view of the instrument without the cover. The grid lines marked on the bottom side of the disc indicated the directions (east, south, west and north) referred to a magnetic compass during the experiment. The cell is located at the center of the upper surface of the disc (arrow).
in width × 12 cm in height) and a cover for the container were fabricated using a 1.2 cm thick smooth plastic plate (Figure 1(A)). The container was placed on an experiment table in a room with constant illumination intensity during the experiment. The room temperature was maintained at ~24℃. A circular plastic disc (22 cm in diameter, 1.2 cm in thickness) was prepared and placed in the container (Figure 1(A)); during the preparation of the disc, it was ensured that both surfaces of the disc were smooth and that the disc had a constant thickness. In order to overcome the influence of gravity on the liquid diffusion along the upper surface of the disc, a sufficiently horizontal position was maintained for the disc by adjusting the experiment table, using a liquid level instrument as a reference. A small inverted bell-shaped cell (~20 µl in volume) was dug at the center of the upper surface of the disc (arrow, Figure 1(B)). The container was filled with deionized water to cover the disc to a water depth of 0.4 cm from the upper surface. 10 µl of 0.5% Toluidine blue solution was carefully loaded into the cell using a pipette. The diffusion pattern was photographed starting within 30 sec of loading the cell and then once every ten minutes until the end of each observation (40 min). The images were analyzed using Nikon image-analysis software (NIS-Elements BR 3.1).
The experiments were conducted in Wuhan City, China (longitude: 114.39˚W; latitude: 30.49˚N). The observations were performed for 24 times per day (once per hour) and repeated on three or four dissimilar days each season. The experiments lasted from December 22, 2011 to March 23, 2013, and included time points spanning all four seasons. The time details for each experiment are presented in Table1
3. RESULTS
Within the first 30 seconds, the loaded toluidine blue solution forms a small round shape in the water (Figure 2(A)) and its shape then extends through diffusion. A large

Table 1 . The time details for each experiment.
The days of the perihelion and aphelion of the earth in 2012 were 2012-1-5 and 2012-7-5, respectively. Each experiment lasted from 9:00 on the first day to 9:00 on the next day. The sun up/down times refer to Beijing time.

Figure 2. Long-term anisotropic (asymmetric) diffusion of toluidine blue solution in water. (A)-(E) A typical diffusion pattern photographed at different time points (0 - 40 min). The clockwise orientation (angles) of the maximum diffusion trend (MDT) over 30 min was measured in reference to the direction of earth’s east, which was defined as 0˚ or 360˚ (D). The directions of earth’s east, south, west and north in reference to earth’s magnetic south and north poles are indicated in A. (F)- (O) Other types of diffusion patterns over 30 min at different time points, showing the variable orientations of the MDT.
anisotropic (asymmetric) diffusion pattern of toluidine blue solution in water was observed (Figures 2(B)-(O)). The clockwise angle between the orientation of the maximum diffusion trend (MDT) over 30 min and the direction of earth’s east (defined as 0˚ or 360˚), referred to the earth’s magnetic south and north poles, was measured (Figure 2(D)). The orientation of the MDT was predominantly in western direction, particularly northwest, in the early spring (Figures 3(A) and (B), right part), but it tended toward the southwest in the late spring (Figures 3(C), right part) and summer (Figures 3(E) and (G), right part), with the exception of the day (July 4, 2012) just before the earth reached its aphelion
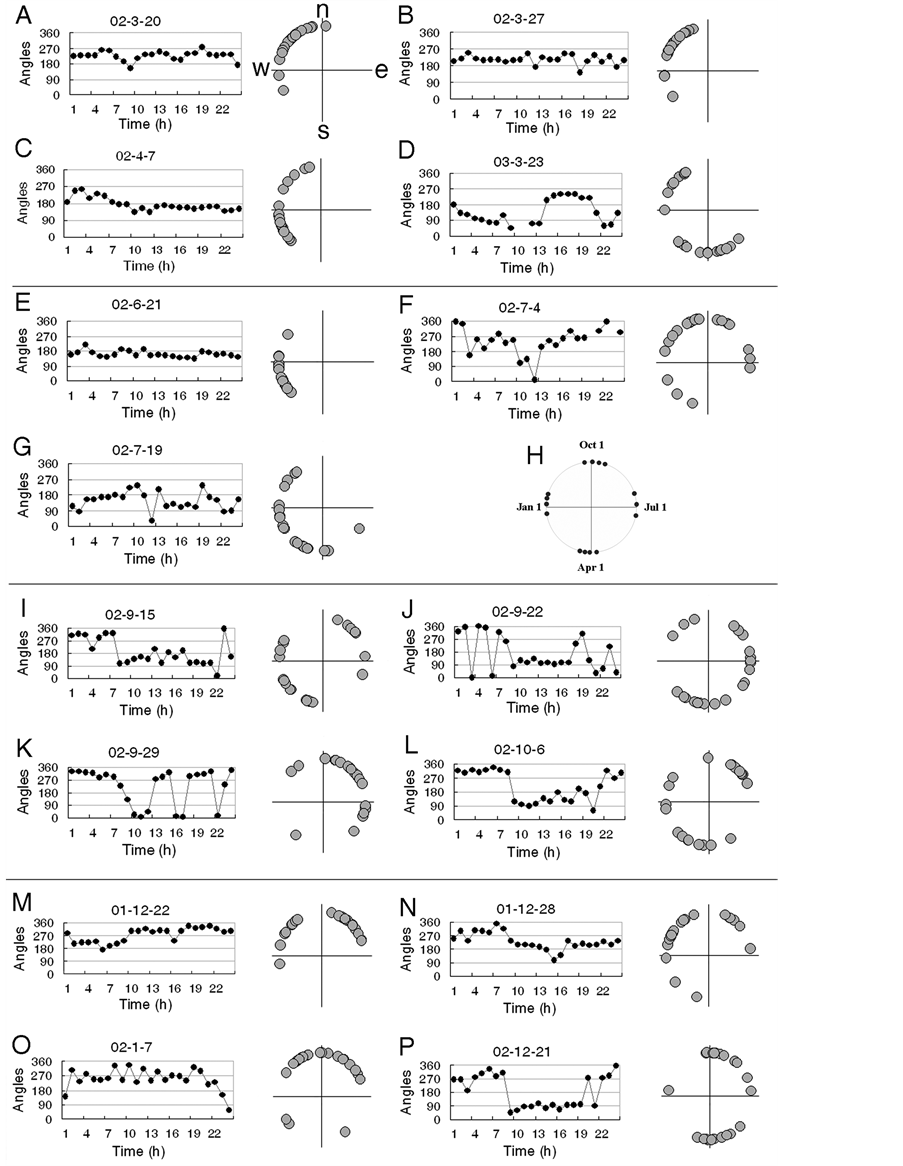
Figure 3. Circadian and seasonal changes in the long-term anisotropic (asymmetric) diffusion of toluidine blue solution in water during the spring (A)-(D), summer (E)-(G), autumn (I)-(L) and winter (M)-(P) periods. (H) The time points for each experiment (see also in Table 1). The leftand right-hand segments of each figure show the circadian change in the orientation of the maximum diffusion trend (MDT) and the orientation distribution, respectively. The notation (e, s, w or n) was used to indicate orientation in (A), which presents east, south, west and north, respectively, and these marks are omitted for the right-hand segments of the other figures. The omission of data in (D) (10:00 and 11:00) and (F) (20:00) indicates that no MDT orientation was clearly detected.
(July 5, 2012, Table 1), during which more variable anisotropic diffusion was found (Figures 3(F), right part). The orientation of the MDT was less favored in approximately one fourth of all directions in the autumn (Figures 3(I)-(L), right part). The orientation of the MDT tended toward the northern direction (northwest or northeast) during the winter (Figures 3(M)-(O), right part). Circadian fluctuations in the orientation of the MDT were also found, and these were large in the autumn (Figures 3(I)-(L), left part), medium in late summer and winter (Figures 3(E)-(G) and 3(M)-(O), left part), and small in spring and early summer (Figures 3(A)-(C) and 3(E), left part). In addition, the orientations of the MDT that were observed during the first year (December 22, 2011 and March 21, 2012) differed somewhat from the observations collected on the most closely corresponding days of the next year (December 21, 2012 and March 23, 2013, Figures 3(D) and (P), right part). Indeed, an isotropic (symmetric) diffusion pattern of the toluidine blue solution was occasionally observed, and in such situations, no clear MDT orientation was detected under the present experimental conditions (Figures 3(D) and (F), left part).
4. DISCUSSION
It has been known for a long time that Brownian motion is not related to any effect of the earth’s magnetic field or environmental light for a single particle [8]. Because the diffusion regime in the present study is based on a group of particles, additional experiments were carried out to exclude the effect of earth’s magnetic field by placing magnetized iron close to the sample of toluidine blue solution during diffusion; as a result, no particular orientation of the MDT was observed in these experiments that could be attributed to the field direction of the magnetized iron. In addition, all diffusion experiments were conducted in a dark container to exclude the ambient light interference.
Therefore, our findings naturally imply that the observed circadian and seasonal changes in long-term macroscopic anisotropic (asymmetric) Brownian diffusion are related to earth’s spin and revolution, but an open question is remained to be answered for the theoretical explanation for our findings. Although the observed phenomena in this study share some similar characteristics of chaos and nonlinear dynamics [13], however, it is obvious that our findings could not be completely explained by chaos and nonlinear dynamic theory [13]. A possible explanation for the present findings is that the directional movement of a “Universe field”, which has been proposed in a recent theoretical model [12], could be the mechanism. These experimental data seem to support such the possibility that the movement direction of such a “Universe field” may be consistent with the direction from the perihelion to the aphelion of the earth. A schematic model for providing an explanation for these findings is shown in Figure 4. According to the previous theoretical model [12] and the present findings, it can be suggested that the random oscillations of Brownian motion of particle in a liquid or gas may be the result of wave-like oscillations of the “Universe field” at the small scale (microscopic scale), whereas the longterm anisotropic Brownian motion may be an effect of the directional movement of the “Universe field” at the large scale (macroscopic scale); both of these effects of the “Universe field” are a result of the universe collapse force (UCF) that arises from the interaction and the transformation between the universal matter (such as atoms or molecules, etc.) and the “Universe field”, and has been proposed to be represented by four different aspects of the fundamental forces (universal gravitation, electromagnetic force, strong force and weak force and) at the large or small scales [12]. Therefore, the circadian and seasonal changes in the anisotropic (asymmetric) direction of Brownian diffusion are caused by the effect of a variable composite force, which primarily consists of the three forces shown in Figure 4, which are different types of UCFs and determined by the changes in di-
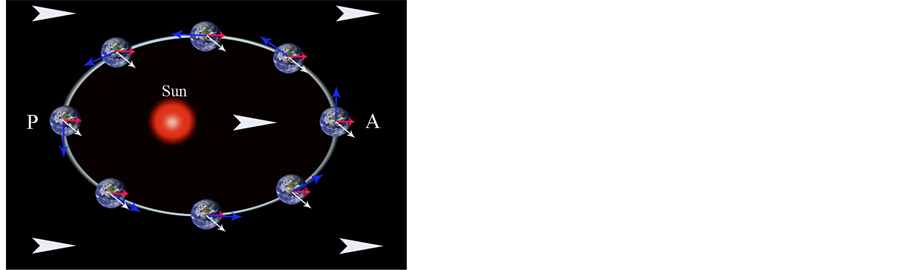
Figure 4. A proposed model for the explanation of the circadian and seasonal changes in long-term anisotropic (asymmetric) diffusion of toluidine blue solution in water. The proposed three kinds of forces are the universe field’s force (red arrows), the earth’s revolution force (blue arrows) and the earth’s spin force (white arrows), respectively. The universe field’s force maintains a relatively stable direction, and the earth’s revolution force changes direction during the revolution of the earth around the sun, while the earth’s spin force changes direction over the 24 hr period of the earth’s diurnal revolution. The combination of these three forces could result in a composite force, in other words, just an effect (not shown) that exhibits unique circadian and seasonal changes in direction and is responsible for the circadian and seasonal changes in long-term anisotropic diffusion, as shown in this study. The white arrowheads indicate the movement direction of the “Universe field”, which is oriented from the perihelion (P) to the aphelion (A) of the earth, and is responsible for the formation of the universe field’s force.
rections and speeds of universal matters that the “Universe field” is used as a reference.
The results of this study suggest a link between longterm macroscopic anisotropic Brownian motion and the movement of universe; however, it should be emphasized that, of course, to evaluate our findings accurately and confirm such a novel explanation for the origin of Brownian motion, more rigorous experimental crosschecks and the development of a complete mathematical description and explanation of the findings must yet be done. Nevertheless, in view of the implications of these findings, I report here in the hope that it may stimulate and encourage further experimental investigations concerning the directional movement of the “Universe field” and the UCF, which may be of benefit to the understanding of not only the true origin of Brownian motion but also other fundamental unexplained physical questions, from the universal movement law to biological phenomena. For example, the elliptical revolution of planets around a sun may be the consequence of the directional movement of the “Universe field.”
5. CONCLUSION
Here circadian and seasonal changes in long-term macroscopic anisotropic (asymmetric) Brownian motion of a toluidine blue colloid solution in water in two dimensions were demonstrated, suggesting that such an anisotropic Brownian motion may be related to an effect of the directional movement of “Universe field”, and thereby providing new interpretations for the true origin and potential applications of Brownian motion.
ACKNOWLEDGEMENTS
This work was supported by the Research Foundation of the SouthCentral University for Nationalities (XJS09001).