Paper Menu >>
Journal Menu >>
 Modern Mechanical Engineering, 2011, 1, 69-76 doi:10.4236/mme.2011.12009 Published Online November 2011 (http://www.SciRP.org/journal/mme) Copyright © 2011 SciRes. MME Application of Linear Model Predictive Control and Input-Output Linearization to Constrained Control of 3D Cable Robots Ali Ghasemi Member of Young Researchers Club, Science and Research Branch, Islamic Azad University, Tehran, Iran E-mail: ali.ghasemi.g@gmail.com Received September 3, 2011; revised October 13, 2011; accepted October 25, 2011 Abstract Cable robots are structurally the same as parallel robots but with the basic difference that cables can only pull the platform and cannot push it. This feature makes control of cable robots a lot more challenging com- pared to parallel robots. This paper introduces a controller for cable robots under force constraint. The con- troller is based on input-output linearization and linear model predictive control. Performance of input-output linearizing (IOL) controllers suffers due to constraints on input and output variables. This problem is suc- cessfully tackled by augmenting IOL controllers with linear model predictive controller (LMPC). The effect- tiveness of the proposed method is illustrated by numerical simulation. Keywords: Cable Robots, Input-Output Linearization, Linear Model Predictive Control 1. Introduction After a motion simulator with parallel kinematic chains was introduced in 1965 by D. Stewart [1], parallel mani- pulators received more and more attention because of their high stiffness, high speed, high accuracy, compact and high carrying capability [2]. They have been used widely in the fields of motion simulators, force/torque sensors, com- pliance devices, medical devices and machine tools [3,4]. A parallel robot is made up of an end-effector, with n degrees of freedom, and a fixed base linked together by at least two independent kinematic chains [5]. Actuation takes place through m simple actuators. Parallel robots drawbacks are their relatively small workspace and kine- matics complexity. Cable robots are a class of parallel robots in which the links are replaced by cables. They are relatively simple in form, with multiple cables attached to a mobile plat- form or an end-effector. Cable robots posses a number of desirable characteristics, including: 1) stationary heavy components and few moving parts, resulting in low iner- tial properties and high payload-to-weight ratios; 2) in- comparable motion range, much higher than that obtained by conventional serial or parallel robots; 3) cables have negligible inertia and are suitable for high acceleration applications; 4) transportability and ease of disassembly/- reassembly; 5) reconfigurability by simply relocating the motors and updating the control system accordingly; and, 6) economical construction and maintenance due to few moving parts and relatively simple components [6,7]. Con- sequently, cable robots are exceptionally well suited for many applications such as handling of heavy materials, inspection and repair in shipyards and airplane hangars, high-speed manipulation, rapidly deployable rescue robots, cleanup of disaster areas, and access to remote locations and interaction with hazardous environments [6-12]. For these applications conventional serial or parallel robots are impractical due to their limited workspace. However, cables have the unique property—they can- not provide compression force on an end-effector. Some research has been previously conducted to guarantee po- sitive tension in the cables while the end-effector is moving. The idea of redundancy was utilized in cable system con- trol [13,14]. This paper introduces a controller for cable robots un- der force constraint. By considering, linear model predic- tive covers different constraint such as input constraints. The goal is to apply the linear model predictive control to the input-output linearized system to account for the constraints. A variety of nonlinear control design strategy has been proposed in the past two decades. Input-output lineariza- tion (IOL) and nonlinear model based control are the most widely studied design techniques in nonlinear control. The  A. GHASEMI 70 central idea of the input–output linearization approach is to algebraically transform the nonlinear system into lin- ear one and apply a suitable linear control design techni- que [15,16]. LMPC is primarily developed for process control. There- fore its application in robot control has less been reported. The incipient interest in the applications of MPC dates back to the late 1970s. In 1978, Richalet et al. [17], pre- sented the Model Predictive Heuristic Control (MPHC) method in which an impulse response model was used to predict the effect at the output of the future control ac- tions. Linear model predictive control refers to a class of control algorithms that compute a manipulated variable pro- file by utilizing a linear process model to optimize a lin- ear or quadratic open-loop performance objective subject to linear constraints over a future time horizon. The first move of this open loop optimal manipulated variable pro- file is then implemented. This procedure is repeated at each control interval with the process measurements used to update the optimization problem. During 1980s, MPC quickly became popular particularly in chemical process industry due to the simplicity of the algorithm and to the use of the impulse or step response model, which is pre- ferred, as being more intuitive and requiring no previous information for its identification [18]. A cable-suspended robot is actuated by servo motors that control the tensions in the cables. A major disadvan- tage of cable robots is that each cable can only exert ten- sion. This constraint leads to performance deterioration and even instability, if not properly accounted for in the control design procedure. Due to this feature, well known results in robotics for trajectory planning and control are not directly applicable to them. Several approaches in- cluding a lyapunov based controller with variable gains and a feedback linearizing controller with variable gains [19], feedback linearization together with method of ref- erence signal management [20], lyapunov based sliding controller with method of signal management [21] have been suggested to satisfy the positive tension in the ca- bles while the platform is moving. In this paper a linear model predictive control is ap- plied to linearized model. Model predictive control, a com- puter control algorithm that utilizes an explicit model to predict the future response of a system is an effective tool for handling constrained control problems. 2. Kinematics Modeling of the Cable Robots The kinematic notation of a spatial cable-driven manipu- lator is presented in Figure 1, where Pi and Bi are two attaching points of the ith cable to the platform and the base, respectively. ai represents the position vector of Bi in the base frame and bi shows the position vector of the cable connection in the platform frame. Therefore, Ti = ai –R bi –c is the vector representing the length of each cable and li is the direction of tension force along each cable, where c is the position vector of mass center of platform parameterized. R is the rotation matrix between the two frames, the base and the moving, Figure 1. 3. System Dynamics The inertia of each link of cable robots is negligible com- pared to that of the platform because the so-called link is just a cable or wire. Therefore, the dynamics of the links can be ignored which will significantly simplify the dy- namic model of the manipulator. One can derive the New- ton-Euler equations of motion of the manipulator with res- pect to the center of mass on the platform as follows [10] 1 1 () n ext i i n extii i i F mamc fmgT nis number ofcables MI I Rbf lII (1) where m and I are the mass and inertia tensor of the platform including any attached payload; g is the gravity acceleration vector; and fext and τext are external force and moment vectors applied to the platform. and α are the linear and angular acceleration vectors of the platform; Ti and fi are the force vector and force value of the ith cable. Equation (1) can be rewritten into a compact form as: c M xCxD Ju (2) where 33 33 33 33 33 33 00 0,, 00 ext ext mI II fm MC g D Figure 1. General kinematics of a cable robot. Copyright © 2011 SciRes. MME  71 A. GHASEMI 1 ll 11 , nT nn jacopian matrix Rb lRbl JJ 1 n f u f I3*3 is a 3*3 identity matrix and 0 0 0 z y z x yx I II I II I Equation (2) can be written into a steady state form as: (3) where XFGu yEXhX 6* 11 0 ,, n x x x XF G xMCxD yI M J with constraints he difficulty of the tracking control design can be re- di between the output y an where LF h (X) and Lgj h (X) are the Lie derivatives of In this way, we can write all plant’s input-output equa- tio max 0uu 4. Input-Output Linearization T duced if we can find a direct and simple relation between the system output y and the control input u. Indeed, this idea constitutes the intuitive basis for the so-called input -output linearization approach to nonlinear control design. This article is aimed to use the LMPC which covers fferent constraints such as input constraints. Because of LMPC is usually used for linear discrete systems. In the beginning we will linearize the dynamics equations based on in Input-Output Linearization. To generate a direct relationship d the input u, Differentiate the output yi with respect to time t in Equation (3), we have n 1j iF i gij j yLhX Lhut i i hi(X) with respect to F(X) and gj(X), respectively. If Lgjhi(X) = 0, yi = LF hi (X) then the ri th derivative of yi can be represent in the following form. n rr r 1 1 ii i j iF i gFij j yLhX LLhut ns as 11 11 1 1 11 11 11 11 nF qqq q FnF rr rr gF g F rrr r qFqgqg q LL hLL h yLh u yLhLLhLLh (4) where q and ri are the number of degree of freedom of the robot and the relative order of the plant, respectively. Equation (4) can be represented in the following com- pact form: vPWu Now u can be obtained as where : 1 uWWW vP W is the pseudo inverse of W. For a cable robotic system, it can be easily shown that th 1 TT WWWW e system has no zero dynamics. Therefore, the decoup- ling matrix W is full rank and the control law is well defined and a suitable change of coordinates T X where 112 2 T qq X yyyyy y yiel loop sy 21, i yx ri ds a closed- stem in the normal form [15]. ,q 1q rr n A Bv yH . Linear Model Predictive Control hown in Fi- 5 he basic structure of MPC to implement is sT gure 2 A model is used to predict the future plant outputs, based on past and current values and on proposed future control actions. These actions are calculated by optimizer taking into account the cost function as well as con- straints. The optimizer is another fundamental part of the strategy as it provides the control action. each component of this structure is described in more detail In the fol- lowing of this article. Figure 2. Basic structure of MPC. Copyright © 2011 SciRes. MME  A. GHASEMI 72 The goal tive control to is to apply the linear model predic the input-output linearized system to account for the constraints. Since the linear model predictive is more na- turally formulated in discrete time, the linear subsystem in (5) is discretized with a sampling period T to yield 1kAkBvk dd d yk H k (6) where Ad ,Bd and Hd are obtained directly from the con- t relation between u(k) and v( This mapping can be rewritten in the followingrm .1. Constraint Mapping hen linear model predictive control is applied to the tinuous-time matrices [22]. Also, the state-dependen k) is obtained as r vk Lh r FGF X kLLhXkuk fo vkP X kWX kuk 5 W system, it is necessary to map the constraints from the original input space to linearized system. By considering v is a new input to be determined, To obtain constraints on the new input, The input constraint mapping is perfor- med using input–output linearization law and the current state measurement x(k). The transformed constraints can be determined on each sampling period by solving the following optimization problem: min max (|) min max 01 max 01 uk jk uk jk k WXkjkukjkjN vkjk PXkjk WXkjkukjkjN uukjju (7) where Z (k + j|k) is the predicted value of the system s pr minvkjk PXkj tate (Z) at time k + j based on the information available at time k. Note that the variable X (k + j|k) cannot be calculated ovided that the input sequence is calculated, which is not possible until the constraints are specified. Therefore, at the beginning (k = 0), the input constraint over the entire control horizon can be presented by: min min 1, ,1 max max 1, ,1 jN jN k vkjkvkk (8) Then, we use inputs calculated at last sampling time to de vkjkvk termine future constraints at the current sampling time. Therefore, Equation (7) will be changed into Equation (9). min (|) max (|) min max 1] 0 1 max 1 101 uk jk uk jk W XkjkukjkjN vkjkPXkjk WXkjkukjk jN uukjju min 1vkjkPXkjk (9) Now Equation (9) can be solved to obtain vmin(k+ an .2. Linear Model Predictive Control Design he goal is to apply LMPC to the linearized system to j|k) d vmax(k + j|k). If W(i,j) is positive, the control u(j) must be the smallest value for vmin and the largest value for vmax and if W(i,j) is negative, then it must be the largest value for vmin and the smallest value for vmax. 5 T account for these constraints. Now the model (6) is used in the infinite horizon linear model predictive strategy pro- posed by Muske and Rawlings [23]. Therefore, the open- loop optimal control problem that the input control found by minimizing the infinite horizon criterion, can be ex- pressed as ddd d (|) 1 dd min ()() 1 1 TT Vkk j T T kjkHQHkjk vk jkvSvk jkv vk jkvk jk Rvk jkvk jk (10) where ξd and vd are target values for ξ and v, respectively, o mi- ni sion vector is defined as V(k|k) = [v(k|k) v( and Q,S, and R, are positive semi definite matrices. In order to obtain value v(k + j|k) it is necessary t mize the functional of Equation (10) to do this value of the predicted output are calculated as function of pas va- lues of inputs and outputs and future control signals ob- tain an expression whose minimization leads to the looked for values. The deci k+1|k) v(k+N-1|k)]T, where N is the control horizon. All future moves beyond the control horizon are set equal to the target value vd. As discussed in [23], the ma- trix Ad is unstable and in order for the linear model pre- dictive problem to have a feasible solution it is necessary to impose the equality constraint ξ(k + N|k) = ξd . To ob- tain a finite set of decision variables, inputs beyond the control horizon are set equal to the desired value: v(k + j|k) = vd, j ≥ N. Therefore, the infinite horizon linear Copyright © 2011 SciRes. MME  A. GHASEMI Copyright © 2011 SciRes. MME 73 model predictive problem Equation (10) can be written as a finite horizon problem. 12 NN ddddd A BA BB EE ddd 0 i Ni TT N i dd (|) 1 ddd d 1 dd 1 1 1 T Vkk T NT j T T SvkNkv kjkHQHkjk vk jkvSvk jkv vk jkvk jk Rvk jkvk jk d K AHQHA min 1vkNkv (11) This optimization problem must be solved subjected to th The solution of Equation (13) belongs to the regular system. To find the solutions of the tracking one, that of the regular system should be shifted into the origin of the system to the steady state described by ξd, and vd. The desired values must lie within the feasible region defined by input constraints for linear model predictive control and minimize the control effort (Equation (15)). e following constraints: min min d vk jkvkjkvkjk (12) Straightforward algebraic manipulation of quadratic ob (13) where Equation (13) should be solved subjected to the fol- lo 2 2 min( 0 0 d T mm mmds U T mm mmd ddd I UU Q IUU Uv kNk jective function of the corresponding regular system presented in Equation (11) results in the following stan- dard quadratic program form: min 2 TT VHHV V GG 2*2 : 0 0 0 dd d d d mm d subject to IAB Uy H DD UC (15) |1 Vk kk FFvk Uand Qs are desired value of the input and a positive definite matrix, respectively. Therefore control law is the summation of the answers of Equation (13) and Equation (15) which can be shown in the following form. 1 0 0 , 0 T dNd T dd S BK A FF BKA GG ( ( dd d ukWX kkvkkPXkk WXkkvkk PXkk (16) wing constraints: Figure 3 shows schematic of the proposed structure control. N d DD VCC EE VAk (14) where by considering max max 6* 6* min min 1 ,, 1 N N vkk vkNk I Ivkk vkNk DD CC Figure 3. Schematic of control structure. 0 0 1 2 12 22 12 000 2 2 N N TTTTT dN dddNdddd TT TT dN dddNdddd TNTN T ddd ddddd BK ABSBKBRS BAKB BKA BBKABBKBRS HH 2BKBRS BAKBSBAKB 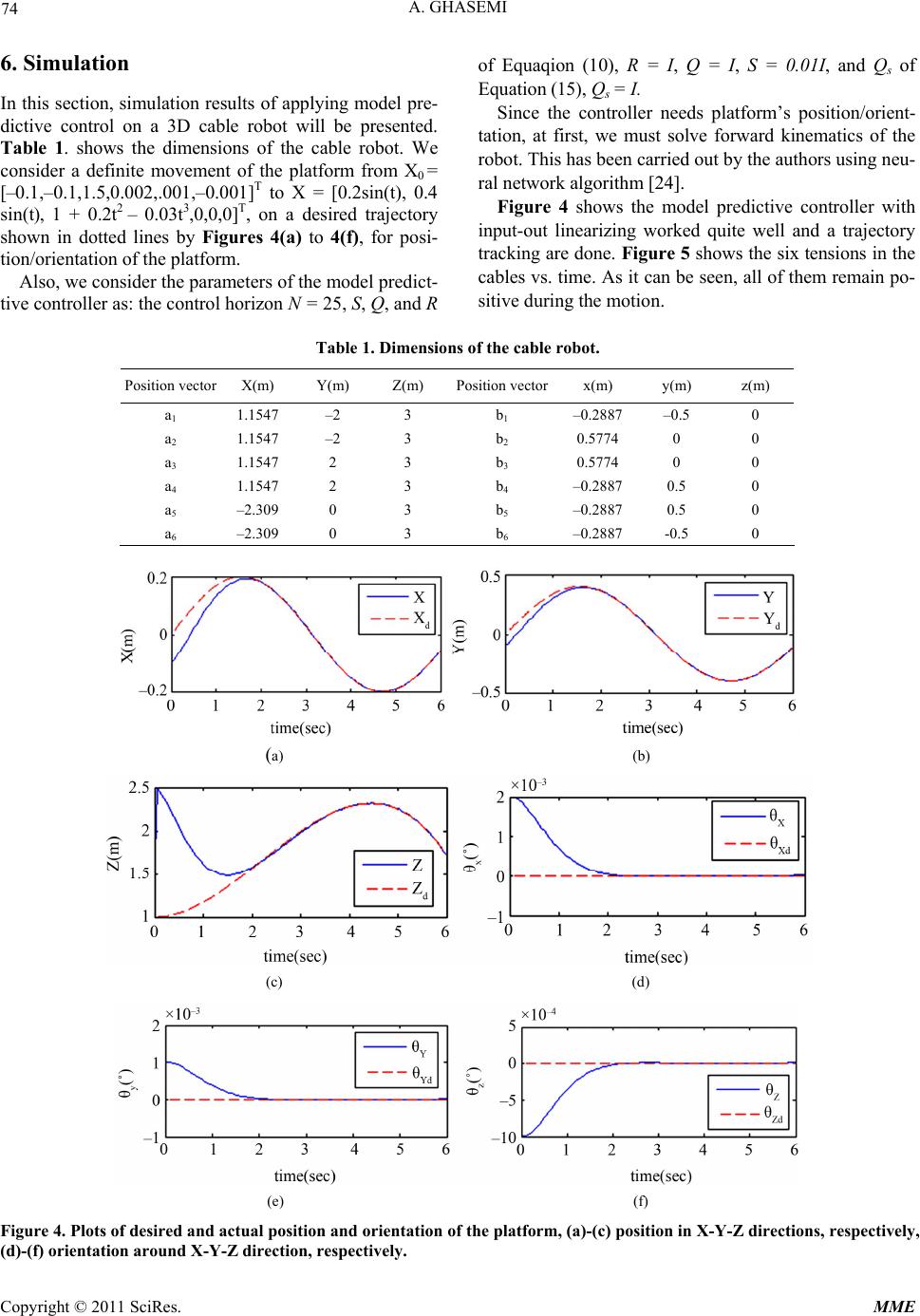 A. GHASEMI 74 6. Simulation In this section, simulation results of applying model pre- dictive control on a 3D cable robot will be presented. Table 1. shows the dimensions of the cable robot. We consider a definite movement of the platform from X0 = 2,.001,–0.001]T to X = [0.2sin(t), 0.4 03t3,0,0,0]T, on a desired trajectory of Equaqion (10), R = I, Q = I, S = 0.01I, and Qs of Equation (15), Qs = I. Since the controller needs platform’s position/orient- tation, at first, we must solve forward kinematics of the robot. This has been carried out by the authors using neu- ral network algorithm [24]. quite well and a trajectory tra s of t Po [–0.1,–0.1,1.5,0.00 in(t), 1 + 0.2t2 – 0.s shown in dotted lines by Figures 4(a) to 4(f), for posi- tion/orientation of the platform. Also, we consider the parameters of the model predict- tive controller as: the control horizon N = 25, S, Q, and R Table 1. Dimension Position vector X(m) Y(m) Z(m) Figure 4 shows the model predictive controller with input-out linearizing worked cking are done. Figure 5 shows the six tensions in the cables vs. time. As it can be seen, all of them remain po- sitive during the motion. he cable robot. sition vectorx(m) y(m) z(m) a1 1.1547 –2 3 b1 –0.2887–0.5 0 a2 1.1547 –2 3 a 1.1547 2 3 b2 0.5774 0 0 3b3 0.5774 0 0 a4 1.1547 870.5 0 a –2.309 0 3 b –0.28870.5 0 – 2 3 b4 –0.28 5 a6 5 b6 –2.309 0 3 0.2887-0.5 0 (a) (b) (c) (d) (e) (f) Figure 4. Plots of desired and actual position and orientation of the platform, (a)-(c) position in X-Y-Z directions, respectively, (d)-(f) orientation around X-Y-Z direction, respectively. Copyright © 2011 SciRes. MME  75 A. GHASEMI (a) (b) (c) (d) (e) (f) 7. Conclusions In this paper, a linear model predictive controller toge- ther with an input-output linearizing control strategy for a constrained robotic system, a 3D cable robot, was de- veloped and evaluated. The control system is comprised of: 1) an input-output linearizing controller that accounts for cable robot nonlinearities; 2) a constraint mapping sche- e that transforms the actual input onstraints on the feedback linearized sy near model predictive controller that provides explicit nput constraints. The simulation re- ectiveness of the proposed method. It Figure 5. Plots of tension trajectories. m c constraints into input stem; and 3) a li compensation for i ults showed the effs is worth nothing that this approach can be extended for the redundant cable robots. 8. References [1] D. Stewart, “A Platform with Six Degrees of Freedom,” Proceedings of the Institution of Mechanical Engineer, Vol. 180, No. 15, 1965, pp. 371-386. doi:10.1243/PIME_PROC_1965_180_029_02 [2] J. -P. Merlet, “Parallel Robots, Solid Mechanics and Its 2006, pp. 890-902. [7] A. T. Riechel and I. Ebert-Uphoff, “Force-Feasible Work- space Analysis for Underconstrained Pointmass Cable Robots,” Proceedings of I Applications,” Kluwer, Norwell, 2001. [3] J. -P. Merlet, “Still a Long Way to Go on the Road for Parallel Mechanisms,” A Keynote Speech at Design En- gineering Technical Conferences, Montreal, 29 Septem- ber-2 October 2002. [4] J. -P. Merlet, “Parallel Robots, Open Problems,” INRIA Sophia-Antipolis, France. http://www.-sop.inria.fr [5] L. -W. Tsai, “Robot Analysis, The Mechanics of Serial and rs,” Wiley, New York, 1999. A. T. Riechel and I. Ebert-Uphoff, “Wrench- rkspace Generation for Cabledriven Robots,” Journal of Intelligent and Robotic Systems, Vol. 22, No. 4, EEE International Conference on Robotics and Automation, New Orleans, 26 April-1 May 4962. W. Choe, S. Tanaka and S. R. Pandian, [9] P. Lafourcade, M. Llibre and C. Reboulet, “Design of a Par- Parallel Manipulato [6] P. Bosscher, Feasible Wo 2004, pp. 4956- ]S. Kawamura,[8 “Development of an Ultrahigh Speed FALCON Using Wire Drive System,” In Proceedings of the 1995 IEEE International Conference on Robotics and Automation, 21-27 May 2003, pp. 215-220. Copyright © 2011 SciRes. MME  A. GHASEMI 76 mental Issues and plication of HIL Microgravity Con- allel Wire-Driven Manipulator for Wind Tunnels,” In Proceedings of the Workshop on Funda Future Research Directions for Parallel Mechanisms and Manipulators, Quebec, 3-4 October 2002, pp. 187-194. [10] X. Diao, O. Ma and R. Paz, “Study of 6-DOF Cable Ro- bots for Potential Ap tact-Dynamics Simulation,” In Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit, Keystone, 21-24 August 2006, pp. 1097-1110. [11] P. Gallina, G. Rosati and A. Rossi, “3-D.O.F. Wire Driven Planar Haptic Interface,” Journal of Intelligent and Ro- botic Systems,Vol. 32, No. 1, 2001, pp. 23-36. doi:10.1023/A:1012095609866 [12] J. Albus, R. Bostelman and N. Dagalakis, “The NIST Robocrane,” Journal of Robotic Systems, Vol. 10, No. 5, 1993, pp. 709-724. doi:10.1002/rob.4620100509 [13] Y. Q. Zheng, “Workspace Analysis of a Six DOF Wire- Driven Parallel Manipulator,” Proceedings of the WORK- SHOP on Fundamental Issues and Future Research De- rection for Parallel Mechanisms and Manipulators, Que- bec, 3-4 October 2002, pp. 287-293. [14] W. J. Shiang, D. Cannon and J. Gorman, “Dynamic Analysis of the Cable Array Robotic Crane,” Proceedings of the IEEE International Conference on Robotics and Automation, Detroit, 10-15 May 1999, pp. 2495-2500. [15] J. J. Slotine and W. Leiping, “Applied Nonlinear Control,” Prentice Hall, Englewood Cliffs, 1991. [16] H. Khalil, “Nonlinear Systems,” 3rd Edition, Prentice-Hall, Upper Saddle River, 2002. [17] J. Richalet, A. Raault, J. L. Testud and J. Papon, “Model Predictive Heuristic Control: A pplication to Industry Processes,” Automatica, Vol. 14. No. 2, 1978, pp. 413-428. doi:10.1016/0005-1098(78)90001-8 [18] C. E. Garcia, D. M. Prett and Morari, “Model Predictive Control: Theory and Practice—a Survey,” Automatica, Vol. 25, No. 3 1989, pp. 335-348. doi:10.1016/0005-1098(89)90002-2 [19] A. B. Alp and A. K. Agrawal, “Cable Suspended Robots: ce on Robotics and Design, Planning and Control,” International Conference on Robotics Robotics & Automation, Washington, DC, 9- 13 May 2002, pp. 556-561. [20] S. R. Oh and A. K. Agrawal, “Controller Design for a Non-redundant Cable Robot Under Input Constraint,” ASME International Mechanical Engineering Congress & Expo- sition, 16-21 November 2003, Washington, DC. [21] S. R. Oh and A. K. Agrawal, “A Control Lyapunov Ap- proach for Feedback Control of Cable-Suspended Ro- bots,” IEEE International Conferen Automation, 10-14 April 2007, pp. 4544-4549. [22] F. Franklin, J. Powell and L. Workman “Digital Control of Dynamic Systems” 2nd Edition, Addison Wesley, Bos- ton, 1994, pp. 40-70. [23] K. R. Muske and J. B. Rawlings, “Model predictive con- trol with linear models,” AIChE Journal, Vol. 39, No. 2, 1993, pp. 262-287. doi:10.1002/aic.690390208 [24] A. Ghasemi, M. Eghtesad and M. Farid “Neural Network Solution for Forward Kinematics Problem of Cable Ro- bot,” Journal of Intelligent and Robotic Systems, Vol. 60, No. 2, 2010, pp. 201-215. doi:10.1007/s10846-010-9421-z Copyright © 2011 SciRes. MME |

