Received 14 September 2015; accepted 28 August 2016; published 31 August 2016

ABSTRACT

Within the optimal production and hedging decision framework, Lien compares the exponential utility function with its second order approximation under the normality distribution assumption. In this paper, we first extend the result further by comparing the exponential utility function with a 2n-order approximation for any integer n. We then propose an approach with illustration to find the smallest n that provides a good approximation.

Keywords:

Exponential Utility Function, Optimal Production, Hedging, 2n-Order Approximation

1. Introduction

Using polynomials to approximate the expected utility function is one of the important issues in finance (see, for example, Feldstein [1] , Samuelson [2] , Levy and Markowitz [3] , Pulley [4] , Kroll, Levy, and Markowitz [5] , and Hlawitschka [6] ). Although there are many alternative techniques, it is more efficient to use a polynomial to approximate the utility function. To demonstrate the differences in optimal production and hedging decisions, Lien [7] compares the exponential utility function with its second order approximation under the normality distribution assumption. In this paper, we consider a higher order approximation and demonstrate the uniform convergence. We then provide a method to obtain the smallest n with good approximation result.

2. The Model

Suppose that, at time 0, a producer intends to produce q units of a commodity that are planned to be sold at time 1. The production cost is c(q) and there is no production risk. we assume that the price, , of the commodity at time 1 is a random variable following a normal distribution such that In addition, there is a corresponding futures contract for the commodity that matures at time 1. The price of the futures contract is b at time 0. To hedge against the price risk, the producer sells h units of the futures contract at time 0. Let 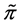denote the profit for the producer at time 1, we have

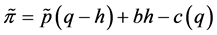. (2.1)

We further assume that the hedger has an exponential utility function u(.) such that

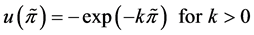. (2.2)

where k is the Arrow-Pratt risk aversion coefficient. Consequently,

, (2.3)

where.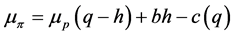

It is well known in the literature that the firm’s optimal production decision 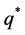depends neither on the risk attitude of the firm nor on the underlying price distribution (i.e., the so-called separation theorem). Specifically, the optimal production decision 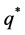is determined by 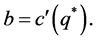Moreover, when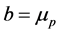, the optimal futures position will be equal to the optimal production decision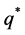; that is, the firm should completely eliminate its price risk exposure by adopting a full-hedge. To explore the effect of a polynomial approximation of the exponential utility function, we follow Lien [7] and allow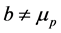. We first discuss the second-order approximation in the next section.

3. Second-Order Approximation

Following Tsiang [8] and Gilbert et al. [9] , Lien [7] considers the following second-order approximation:

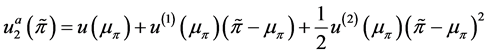, (3.1)

where is the derivative of the utility function u. Under the exponential utility function,

. (3.2)

Let and denote the optimal production level and futures positions that maximize and in (3.2) and (2.3), respectively. Lien [7] shows that if, then and if, then. In other words, the deviation between the optimal production level and the optimal futures position under the second-order approximation is always smaller than that under the original exponential utility function.

4. 2n-Order Approximation

While it is common to use second-order approximation (see, for example, Pulley [4] ), we ask in this paper whether one could include higher order terms from the Taylor expansion to improve the approximation. We first extend Lien [7] ’s results to fourth-order approximation and replace the utility function in (3.1) by the following fourth-order approximation:

Consequently,

where. For the normal distribution, we have. Therefore, we have

Let be the optimal production level and futures position combination that maximizes. The resulting first-order condition is:

For that maximizes, we have the following:

From the above equation,

(4.1)

Define and incor-

porate Equation (4.1) into the formula of M(h), we get

Thus, Furthermore, Equation (4.1) implies that, when, we have, and henceforth. On the other hand, by definition, and we obtain the following proposition.

Proposition 4.1. Consider a one-period production and futures hedging framework. Given that the producer is endowed with an the exponential utility function and the spot price in the future is normally distributed,

1) if, then,

2)if, then.

We now turn to the general case. Consider the 2n-th order approximation of the exponential utility function u in (2.2):

(4.2)

Upon taking the expectation, we get

where. Under the normal distribution assumption, Therefore,

Let be the optimal production level and futures position combination that maximizes. The corresponding first order condition is:

For, the following condition holds:

From the above equation, we obtain

.

After substituting this equation into the formula of, we get:

Thus,. Furthermore, Equation (4.3) implies that, when, ,

which in turn leads to. By definition,. We conclude that when. Similarly, it can be shown that, when,.The results are summarized in the following proposition:

Proposition 4.2. Consider a one-period production and futures hedging framework. Given that the producer is endowed with an the exponential utility function and the spot price in the future is normally distributed,

1) if, then, and

2) if, then.

5. True Optimal Futures Positions

In this section we compare the optimal futures position under the 2n-order approximation with the true optimal position under the true expected utility function:

Let denote the combination of the optimal production level and the futures position that maximizes. In this case, the objective function can be simplified to and the resulting first-order condition is

From the previous section, we rewrite as follows:

Thus,

implying the sign of is the same as the sign of. As a result, when,. By definition, , and we conclude that when. Similarly, it can be shown that when,. These results are summarized in the following proposition.

Proposition 5.1. Consider a one-period production and futures hedging framework. Given that the producer is endowed with an the exponential utility function and the spot price in the future is normally distributed, we have

1) if, then, and

2) if, then.

6. Choosing the Approximation Order

We now propose an approach to find the smallest n that will provide a good approximation. Since it is well known that the 2n-order approximation can be rewritten as follows:

Let

Thus,. Upon applying the Cauchy convergence principle, we have the following theorem.

Theorem 6.1. Let defined in (2.1) be the profit at time 1 and q be the optimal production level and suppose that and are the optimal futures positions that maximize and in which u and are defined in (2.2) and (4.2), respectively. We have

1) if, then, and

2) if, then,

3) for any, and

4) for any, there exists N such that for all,.

Thus, to obtain a good approximation for, one may apply part (d) of Theorem 6.1. First, we

choose the level of tolerance, , and then compute and to derive. We then select the smallest n to satisfy the condition,.

7. Illustration

Below we present an example to illustrate Theorem 6.1. Consider,. That is, we

assume. Consequently, and Note that

is the solution to the following equation:

which can be rewritten as:

Solving the above quadratic equation, we have

Now, we let, then

The second order condition requires

Thus,

and

If we assume, then

According to the second order condition, we obtain

Thus,. In both cases,.

By using the “solve” function in MATLAB, we find for and for. In both cases,. If we require, the smallest n is 3. That is,. For the cases with general, , k and b, we compile MATLAB codes to find the smallest n such that

and/or The codes are available on request from the authors.

8. Concluding Remarks

In this paper, we analyze a one-period production and hedging decision problem where the producer is endowed with an exponential utility function. Our findings are summarized as follows. First, it is well-known that a normal distribution coupled with an exponential expected utility produces a mean-variance (MV) approach. Meanwhile, a quadratic approximation also leads to a mean-variance approach. Our first finding is that the two approaches lead to different results (see Lien [7] ). Second, since there are only two parameters for a normal distribution, any 2n-order approximation yields a mean-variance model. It is interesting to compare the differences among the results from the exponential expected utility, the quadratic approximation and the 2n-order approximation. We show that, when expanding to the higher order, there is a monotonic convergence. The difference between the result from the quadratic approximation and that from the exponential expected utility is the greatest and shrinks as the approximation order increases. In addition, it is possible to extend the second-order approximation to the 2n-order approximation with a smallest value of n such that the result from the 2n-order approximation is sufficiently close to that from the exponential expected utility.

Lastly, Hlawitschka [6] argues that the usefulness of Taylor series approximations is a strictly empirical issue unrelated to the convergence properties of the infinite series, and, most importantly, that even for a convergent series adding more terms does not necessarily improve the quality of the approximation. We note that our finding suggests the argument from Hlawitschka [6] may not be correct because in our case adding more terms does improve the quality of the approximation and actually when the number of terms increases, the approximation converges to the true value.

Acknowledgements

This research is partially supported by grants from Beijing Normal University, Nanjing University of Aeronautics and Astronautics, University of Texas at San Antonio, Tsinghua University, Asia University, Lingnan University, Hong Kong Baptist University, and Research Grants Council of Hong Kong.

Cite this paper

Xu Guo,Donald Lien,Wing-Keung Wong, (2016) Good Approximation of Exponential Utility Function for Optimal Futures Hedging. Journal of Mathematical Finance,06,457-436. doi: 10.4236/jmf.2016.63036

References

NOTES

^*Corresponding author.