Applied Mathematics
Vol.06 No.11(2015), Article ID:60602,10 pages
10.4236/am.2015.611166
On Elliptic Problem with Singular Cylindrical Potential, a Concave Term, and Critical Caffarelli-Kohn-Nirenberg Exponent
Mohammed El Mokhtar Ould El Mokhtar
Department of Mathematics, College of Science, Qassim University, Buraidah, Kingdom of Saudi Arabia
Email: med.mokhtar66@yahoo.fr, M.labdi@qu.edu.sa
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 September 2015; accepted 24 October 2015; published 27 October 2015
ABSTRACT
In this paper, we establish the existence of at least four distinct solutions to an elliptic problem with singular cylindrical potential, a concave term, and critical Caffarelli-Kohn-Nirenberg exponent, by using the Nehari manifold and mountain pass theorem.
Keywords:
Singular Cylindrical Potential, Concave Term, Critical Caffarelli-Kohn-Nirenberg Exponent, Nehari Manifold, Mountain Pass Theorem

1. Introduction
In this paper, we consider the multiplicity results of nontrivial nonnegative solutions of the following problem 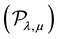
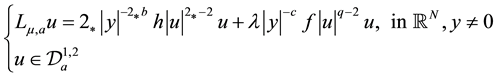
where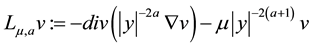 , where each point x in
, where each point x in  is written as a pair
is written as a pair  where k and N are integers such that
where k and N are integers such that 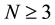 and k belongs to
and k belongs to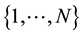 ,
, 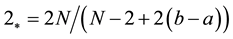
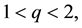
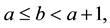
 is the critical Caffarelli-Kohn-Nirenberg exponent,
is the critical Caffarelli-Kohn-Nirenberg exponent,  ,
, 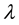
 is a real parameter,
is a real parameter,  , h is a bounded positive function on
, h is a bounded positive function on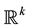 .
. 



Some results are already available for 

therein. Wang and Zhou [1] proved that there exist at least two solutions for 



existence of two solutions of 





Concerning existence results in the case































where 











Before formulating our results, we give some definitions and notation.
We denote by 


and
respectively, with 

From the Hardy-Sobolev-Maz’ya inequality, it is easy to see that the norm 

for all
We list here a few integral inequalities.
The starting point for studying



for any
The second one that we need is the Hardy inequality with cylindrical weights [5] . It states that

It is easy to see that (1.1) hold for any 

where 






Since our approach is variational, we define the functional J on 
with
A point 

with
Here 


Let
From [11] , 
Throughout this work, we consider the following assumptions:
(F) there exist 



(H)
Here, 
In our work, we research the critical points as the minimizers of the energy functional associated to the problem 
Let 
where
Now we can state our main results.
Theorem 1. Assume that





Theorem 2. In addition to the assumptions of the Theorem 1, if (H) hold and 


Theorem 3. In addition to the assumptions of the Theorem 2, assuming




This paper is organized as follows. In Section 2, we give some preliminaries. Sections 3 and 4 are devoted to the proofs of Theorems 1 and 2. In the last Section, we prove the Theorem 3.
2. Preliminaries
Definition 1. Let

i) 

where 
ii) We say that I satisfies the 

Lemma 1. Let X Banach space, and 

i) there exist



ii) there exist 


let 
then c is critical value of J such that
Nehari Manifold
It is well known that J is of class 



Thus, 

Note that 

Lemma 2. J is coercive and bounded from below on
Proof. If

Thus, J is coercive and bounded from below on
Define
Then, for

Now, we split 
We have the following results.
Lemma 3. Suppose that 



Proof. If 


Hence, there exists a Lagrange multipliers 
Thus,
But


Lemma 4. There exists a positive number 

we have
Proof. Let us reason by contradiction.
Suppose 



Moreover, by the Hölder inequality and the Sobolev embedding theorem, we obtain

and

From (2.5) and (2.6), we obtain
Thus
For the sequel, we need the following Lemma.
Lemma 5.
i) For all 


ii) For all 

Proof. i) Let
and so
We conclude that
ii) Let
Moreover, by (H) and Sobolev embedding theorem, we have
This implies

By (2.2), we get
Thus, for all 


For each 

Lemma 6. Let 



i) If


ii) If





Proof. With minor modifications, we refer to [12] .
Proposition 1 (see [12] )
i) For all 



ii) For all 



3. Proof of Theorems 1
Now, taking as a starting point the work of Tarantello [13] , we establish the existence of a local minimum for J on
Proposition 2. For all 


i)
ii) 

Proof. If






Thus, by (3.1), 





We get a contradiction. Therefore, 








there exists 

which contradicts the fact that






4. Proof of Theorem 2
Next, we establish the existence of a local minimum for J on
Lemma 7. For all 



i)
ii) 


Proof. If





This implies
Moreover, by (H) and (2.3) we obtain

where,
such that

This implies that
Now, we prove that 





we have
and this is a contradiction. Hence,
Thus,
Since 




Now, we complete the proof of Theorem 2. By Propositions 2 and Lemma 7, we obtain that 





5. Proof of Theorem 3
In this section, we consider the following Nehari submanifold of
Thus, 
Firsly, we need the following Lemmas
Lemma 8. Under the hypothesis of theorem 3, there exist




Proof. Fix 
Clearly 


If 



where
and
and there exists 




Lemma 9. There exist M, 
and any 
Proof. Let
where
and choosing 


Lemma 10. Suppose 


i) we have
ii) there exists 



Proof. We can suppose that the minima of J are realized by 

i) By (2.3), (5.1) and the fact that
Exploiting the function 





ii) Let
Letting 
we obtain

Let 
and
Proof of Theorem 3.
If
then, by the Lemmas 2 and Proposition 1 ii), J verifying the Palais-Smale condition in

Thus 





Cite this paper
Mohammed El MokhtarOuld El Mokhtar, (2015) On Elliptic Problem with Singular Cylindrical Potential, a Concave Term, and Critical Caffarelli-Kohn-Nirenberg Exponent. Applied Mathematics,06,1891-1901. doi: 10.4236/am.2015.611166
References
- 1. Wang, Z. and Zhou, H. (2006) Solutions for a Nonhomogeneous Elliptic Problem Involving Critical Sobolev-Hardy Exponent in . Acta Mathematica Scientia, 26, 525-536.
http://dx.doi.org/10.1016/S0252-9602(06)60078-7 - 2. Xuan, B.J. (2005) The Solvability of Quasilinear Brézis-Nirenberg-Type Problems with Singular Weights. Nonlinear Analysis, 62, 703-725.
http://dx.doi.org/10.1016/j.na.2005.03.095 - 3. Bouchekif, M. and Matallah, A. (2009) On Singular Nonhomogeneous Elliptic Equations Involving Critical Caffarelli-Kohn-Nirenberg Exponent. Ricerche di Matematica, 58, 207-218.
http://dx.doi.org/10.1007/s11587-009-0056-y - 4. Gazzini, M. and Musina, R. (2009) On the Hardy-Sobolev-Maz’ja Inequalities: Symmetry and Breaking Symmetry of Extremal Functions. Communications in Contemporary Mathematics, 11, 993-1007.
http://dx.doi.org/10.1142/S0219199709003636 - 5. Musina, R. (2008) Ground State Solutions of a Critical Problem Involving Cylindrical Weights. Nonlinear Analysis, 68, 3972-3986.
http://dx.doi.org/10.1016/j.na.2007.04.034 - 6. Badiale, M., Guida, M. and Rolando, S. (2007) Elliptic Equations with Decaying Cylindrical Potentials and Power-Type Nonlinearities. Advances in Differential Equations, 12, 1321-1362.
- 7. Bouchekif, M. and El Mokhtar, M.E.O. (2012) On Nonhomogeneous Singular Elliptic Equations with Cylindrical Weight. Ricerche di Matematica, 61, 147-156.
http://dx.doi.org/10.1007/s11587-011-0121-1 - 8. Terracini, S. (1996) On Positive Entire Solutions to a Class of Equations with Singular Coefficient and Critical Exponent. Advances in Differential Equations, 1, 241-264.
- 9. Tarantello, G. (1992) On Nonhomogeneous Elliptic Equations Involving Critical Sobolev Exponent. Ann. Inst. H. Poincaré Anal. Non. Linéaire, 9, 281-304.
- 10. Wu, T.-F. (2008) The Nehari Manifold for a Semilinear System Involving Sign-Changing Weight Functions. Nonlinear Analysis, 68, 1733-1745.
http://dx.doi.org/10.1016/j.na.2007.01.004 - 11. Kang, D. and Peng, S. (2004) Positive Solutions for Singular Elliptic Problems. Applied Mathematics Letters, 17, 411-416.
http://dx.doi.org/10.1016/S0893-9659(04)90082-1 - 12. Brown, K.J. and Zhang, Y. (2003) The Nehari Manifold for a Semilinear Elliptic Equation with a Sign Changing Weight Function. Journal of Differential Equations, 2, 481-499.
http://dx.doi.org/10.1016/S0022-0396(03)00121-9 - 13. Liu, Z. and Han, P. (2008) Existence of Solutions for Singular Elliptic Systems with Critical Exponents. Nonlinear Analysis, 69, 2968-2983.
http://dx.doi.org/10.1016/j.na.2007.08.073 - 14. Drabek, P., Kufner, A. and Nicolosi, F. (1997) Quasilinear Elliptic Equations with Degenerations and Singularities. Walter de Gruyter Series in Nonlinear Analysis and Applications, Vol. 5, New York.
http://dx.doi.org/10.1515/9783110804775











































































