Advances in Pure Mathematics
Vol.05 No.09(2015), Article ID:58498,3 pages
10.4236/apm.2015.59054
On Congruences Induced by Certain Relations on “Semigroups”
K. V. R. Srinivas
Department of Mathematics, Regency Institute of Technology, Yanam, India
Email: srinivaskandarpa73@gmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 March 2015; accepted 28 July 2015; published 31 July 2015
ABSTRACT
In his paper “On quasi-separative ‘semigroup’s’”, Krasilnikova, Yu. I. and Novikov, B. V. have studied congruences induced by certain relations on a “semigroup”. They further showed that if the “semigroup” is quasi separative then the induced congruence is a semilattice congruence. In this paper we continue the study of these relations and the induced congruences i.e., the congruences induced by certain relations on ‘‘semigroup’s”. In this paper mainly it is observed that if S is a quasi-separative and regular “semigroup” then the necessary and sufficient condition for 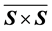 to be the smallest semilattice congruence h is obtained.
to be the smallest semilattice congruence h is obtained.
Keywords:
Cancellative “Semigroup”, Quasi-Separative ‘‘Semigroup’s”, Weakly Cancellative ‘‘Semigroup’s”, Weakly Balanced “Semigroup”

1. Introduction
In this paper “On quasi-separative ‘semigroup’s’”, Krasilnikova Yu. I. and Novikov B.V. have studied congruences induced by certain relations on a “semigroup”. They further showed that if the “semigroup” is quasi-se- parative then the induced congruence is a semilattice congruence. In this paper we continue the study of these relations and the induced congruences. In theorem 2, we have proved that the family of all relatios  which satisfy the conditions from (1) to (3) in Def. 1 of this paper is a complete lattice. In theorem 3, we have also obtained that the family of all congruences which are induced by the relations in
which satisfy the conditions from (1) to (3) in Def. 1 of this paper is a complete lattice. In theorem 3, we have also obtained that the family of all congruences which are induced by the relations in  is a complete lattice. If S is a quasi-separative and regular “semigroup” then the necessary and sufficient condition for
is a complete lattice. If S is a quasi-separative and regular “semigroup” then the necessary and sufficient condition for 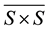 to be the smallest semilattice congruence which is denoted by h (throughout this chapter) is obtained, from which as a corollary that if S is a commutative regular “semigroup” then the congruence induced by the S × S is the smallest semilattice congruence [1] . The authors have remarked that a semilattice of weakly cancellative “semigroup’s” is weakly balanced, it is not known that “whether semilattice of weakly cancellative ‘semigroup’s’ [2] is weakly balanced”, show that the result is not true. It is also observed that every semilattice of weakly cancellative “semigroup’s”, need not be weakly balanced, for this an example is obtained.
to be the smallest semilattice congruence which is denoted by h (throughout this chapter) is obtained, from which as a corollary that if S is a commutative regular “semigroup” then the congruence induced by the S × S is the smallest semilattice congruence [1] . The authors have remarked that a semilattice of weakly cancellative “semigroup’s” is weakly balanced, it is not known that “whether semilattice of weakly cancellative ‘semigroup’s’ [2] is weakly balanced”, show that the result is not true. It is also observed that every semilattice of weakly cancellative “semigroup’s”, need not be weakly balanced, for this an example is obtained.
2. Main Content
The following definition is due to Krasilnikova Yu. I. and Novikov B. V. (see [3] ).
Def 1: Let S be a “semigroup” and Ω be a relation on S satisfying conditions.
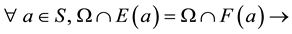 (1)
(1)
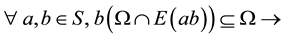 (2)
(2)
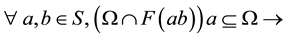 (3)
(3)
where 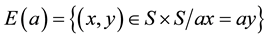 and
and 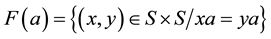
Define a relation 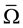 on S corresponding to Ω by
on S corresponding to Ω by 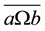 if and only if
if and only if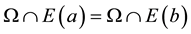 . It is also equivalent to
. It is also equivalent to 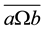 if and only if
if and only if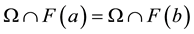 , this relation
, this relation 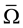 is a congruence on S.
is a congruence on S.
Lemma 2: Let  be the family of all relations on S which satisfy the conditions from (1) to (3) then
be the family of all relations on S which satisfy the conditions from (1) to (3) then 
Proof: Let







Lemma 3: Let 

Proof: Since 







Theorem 4: Let S be quasi-separative and regular “semigroup”. Then 


Proof: Suppose S is quasi-separative and regular and Suppose




























Corollary 5: If S is a commutative regular “semigroup” then
Corollary 6: If S is a completely regular and 



The following is an example of a completely regular “semigroup” in which
Example 7: Let S be a left zero “semigroup” with at least two elements. If 



Theorem 8: In a band S, 
It is natural to ask whether every semilattice congruence on “semigroup” is of the form 

The following example shows that it is not true.
Example 9: Consider the non modular lattice 





Figure 1. ac = bc = 0, take c = f.
The following example shows that 

Example 10: Let 




The following example shows that in non quasi-separative “semigroup’s” there exists 

Example 11: Let S be a non quasi-separative “semigroup”, then 1s is in


It is interesting to note that if S is a left or right zero “semigroup” then

In paper [1] they have remarked that it is not known that whether semilattice of weakly cancellative “semigroup’s” is quasi-separative and weakly balanced. In the following we are giving an example which shows that it is not true i.e. if a “semigroup’s” is isomorphic to a semilattice of weakly cancellative “semigroup’s” then S is a quasi-separative and weakly balanced.
Example 12: Consider the “semigroup” 
Then h-classes are {a, b} and {c, d} which are right zero “semigroup’s” and hence S is a semilattice of weakly cancellative “semigroup’s”, but S is not weakly balanced since


The following is an example of quasi separative “semigroup”, which is not completely regular.
Example 13: Consider the “semigroup” 
where

Thorem 14: Let S be a separative “semigroup”, and 


Proof: Let S be a separative “semigroup” and a Î S such that E(a) is a semilattice congruence. Then for any












Acknowledgements
We are very much thankful to the referees for their valuable suggestions.
Cite this paper
K. V. R.Srinivas, (2015) On Congruences Induced by Certain Relations on “Semigroups”. Advances in Pure Mathematics,05,579-582. doi: 10.4236/apm.2015.59054
References
- 1. Burmistrovich, I.E. (1965) Commutative Bands of Cancellative “Semigroup’s’”. Sib.Mat.Zh., 6, 284-299 (Russian).
- 2. Petritch, M. (1973) Introduction to “‘Semigroup’ Theory”. Merill Books, Columbus.
- 3. Krasilnikova, Yu.I. and Novikov, B.V. (2005) On Quasi-separative “semigroup’s”. “Semigroup” Forum, 70, 347-355.




