Applied Mathematics
Vol.4 No.10C(2013), Article ID:37612,20 pages DOI:10.4236/am.2013.410A3006
Higher Genus Characters for Vertex Operator Superalgebras on Sewn Riemann Surfaces
Max-Planck-Institut für Mathematik, Bonn, Germany
Email: zuevsky@mpim-bonn.mpg.de
Copyright © 2013 Alexander Zuevsky. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 21, 2013; revised June 21, 2013; accepted June 28, 2013
Keywords: Vertex Operator Superalgebras; Intertwining Operators; Riemann Surfaces; Szegö Kernel; Modular Forms; Theta-Functions; Frobenius—Fay and Jacobi Product Identities
ABSTRACT
We review our recent results on computation of the higher genus characters for vertex operator superalgebras modules. The vertex operator formal parameters are associated to local parameters on Riemann surfaces formed in one of two schemes of (selfor tori- ) sewing of lower genus Riemann surfaces. For the free fermion vertex operator superalgebra we present a closed formula for the genus two continuous orbifold partition functions (in either sewings) in terms of an infinite dimensional determinant with entries arising from the original torus Szegö kernel. This partition function is holomorphic in the sewing parameters on a given suitable domain and possesses natural modular properties. Several higher genus generalizations of classical (including Fay’s and Jacobi triple product) identities show up in a natural way in the vertex operator algebra approach.
1. Vertex Operator Super Algebras
In this paper (based on several conference talks of the author) we review our recent results [1-5] on construction and computation of correlation functions of vertex operator superalgebras with a formal parameter associated to local coordinates on a self-sewn Riemann surface of genus ![]() which forms a genus
which forms a genus  surface. In particular, we review result presented in the papers [1-5] accomplished in collaboration with M. P. Tuite (National University of Ireland, Galway, Ireland).
surface. In particular, we review result presented in the papers [1-5] accomplished in collaboration with M. P. Tuite (National University of Ireland, Galway, Ireland).
A Vertex Operator Superalgebra (VOSA) [6-10] is a quadruple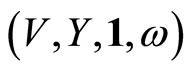 :
:
 ,
,
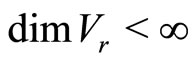 , is a superspace,
, is a superspace, ![]() is a linear map
is a linear map
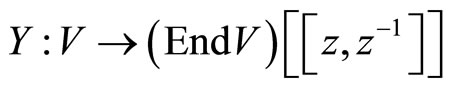 so that for any vector (state)
so that for any vector (state) 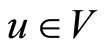 we have
we have
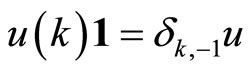 ,
, 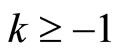 ,
,
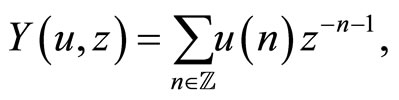
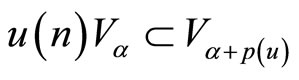 ,
, 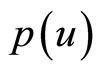 -parity.
-parity.
The linear operators (modes)  satisfy creativity
satisfy creativity

and lower truncation
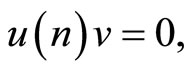
conditions for 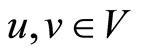 and
and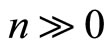 .
.
These axioms identity impy locality, associativity, commutation and skew-symmetry:

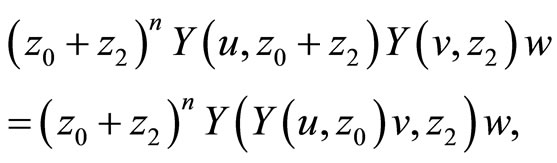


for  and integers
and integers ,
,
 .
.
The vacuum vector 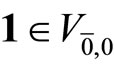 is such that,
is such that, 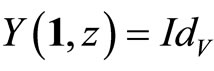 , and
, and  the conformal vector satisfies
the conformal vector satisfies

where  form a Virasoro algebra for a central charge
form a Virasoro algebra for a central charge 
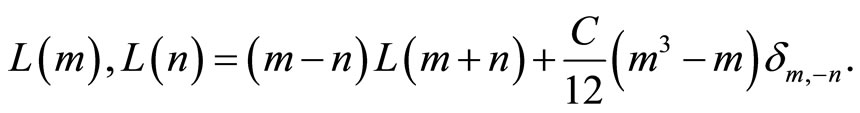
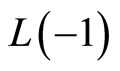 satisfies the translation property
satisfies the translation property

 describes a grading with
describes a grading with
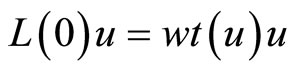 , and
, and 
1.1. VOSA Modules
Definition 1 A  -module for a VOSA
-module for a VOSA  is a pair
is a pair ,
, 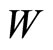 is a
is a 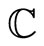 -graded vector space
-graded vector space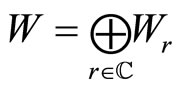 ,
, 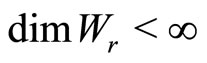 ,
, 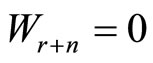 for all
for all 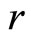 and
and .
.
 ,
,
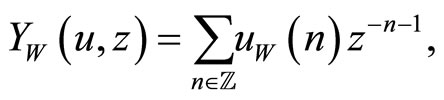
for each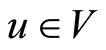 ,
,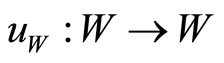 .
.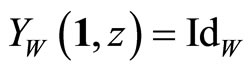 , and for the conformal vector
, and for the conformal vector
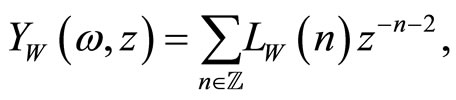
where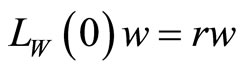 ,
,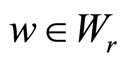 . The module vertex operators satisfy the Jacobi identity:
. The module vertex operators satisfy the Jacobi identity:
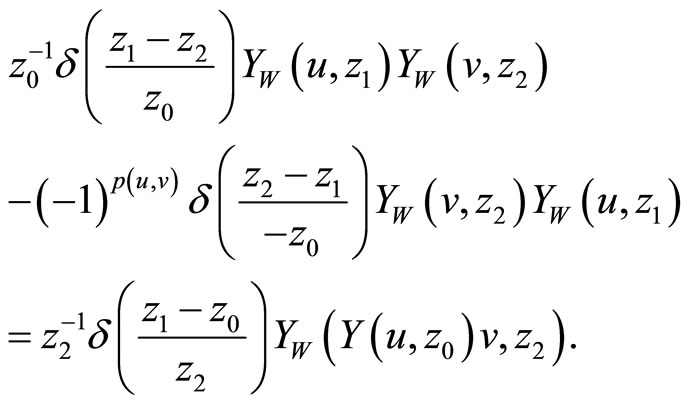
Recall that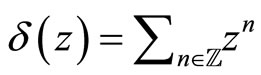 . The above axioms imply that
. The above axioms imply that  satisfies the Virasoro algebra for the same central charge
satisfies the Virasoro algebra for the same central charge 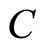 and that the translation property
and that the translation property
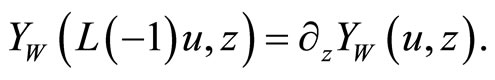
1.2. Twisted Modules
We next define the notion of a twisted  -module [8,11]. Let
-module [8,11]. Let ![]() be a
be a  -automorphism
-automorphism![]() , i.e., a linear map preserving
, i.e., a linear map preserving 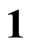 and
and ![]() such that
such that
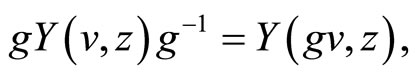
for all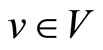 . We assume that
. We assume that 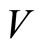 can be decomposed into
can be decomposed into ![]() -eigenspaces
-eigenspaces

where 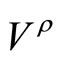 denotes the eigenspace of
denotes the eigenspace of ![]() with eigenvalue
with eigenvalue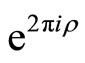 .
.
Definition 2 A ![]() -twisted
-twisted 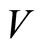 -module for a VOSA
-module for a VOSA 
is a pair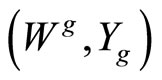 ,
, 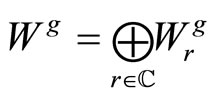 ,
, 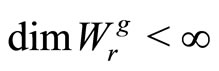 ,
,
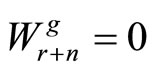 , for all
, for all , and
, and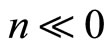 .
.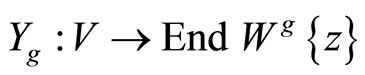 , the vector space of (
, the vector space of (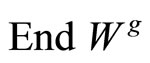 )-valued formal series in
)-valued formal series in 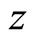 with arbitrary complex powers of
with arbitrary complex powers of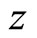 . For
. For 

with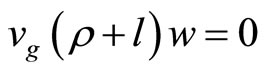 ,
, 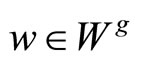 ,
, 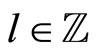 sufficiently large.
sufficiently large.
 ,
, 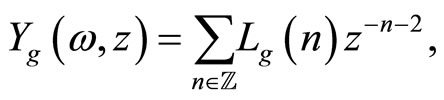
where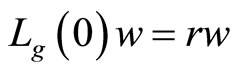 ,
,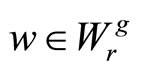 . The
. The ![]() -twisted vertex operators satisfy the twisted Jacobi identity:
-twisted vertex operators satisfy the twisted Jacobi identity:
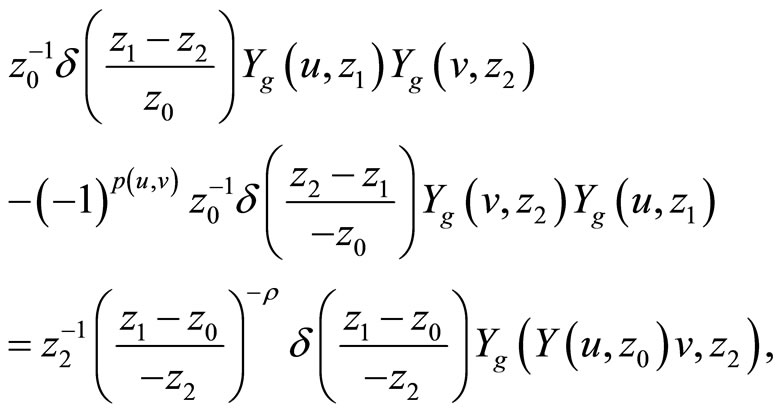
for .
.
1.3. Creative Intertwining Operators
We define the notion of creative intertwining operators in [3]. Suppose we have a VOA 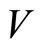 with a
with a 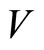 -module
-module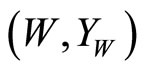 .
.
Definition 3 A Creative Intertwining Vertex Operator  for a VOA
for a VOA 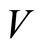 -module
-module 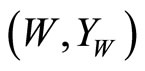 is defined by a linear map
is defined by a linear map
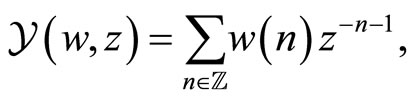
for  with modes
with modes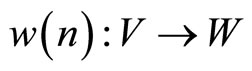 ; satisfies creativity
; satisfies creativity

for 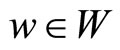 and lower truncation
and lower truncation
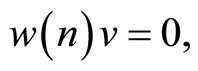
for ,
, 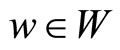 and
and . The intertwining vertex operators satisfy the Jacobi identity:
. The intertwining vertex operators satisfy the Jacobi identity:

for all 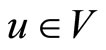 and
and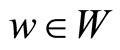 .
.
These axioms imply that the intertwining vertex operators satisfy translation, locality, associativity, commutativity and skew-symmetry:

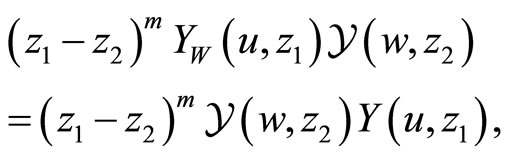
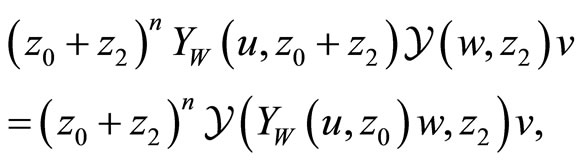


for![]() ,
,  ,
,  and integers
and integers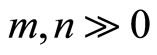 .
.
1.4. Example: Heisenberg Intertwiners
Consider the Heisenberg vertex operator algebra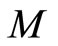 [10] generated by weight one normalized Heisenberg vector
[10] generated by weight one normalized Heisenberg vector ![]() with modes obeying
with modes obeying

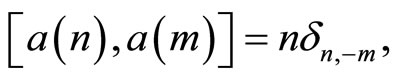 .
.
In [3] we consider an extension 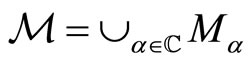 of
of 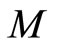 by its irreducible modules
by its irreducible modules 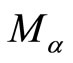 generated by a
generated by a 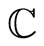 -valued continuous parameter
-valued continuous parameter ![]() automorphism
automorphism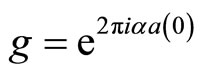 .
.
We introduce an extra operator 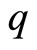 which is canonically conjugate to the zero mode
which is canonically conjugate to the zero mode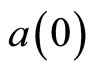 , i.e.,
, i.e.,
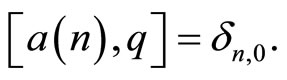
The state  is created by the action of
is created by the action of  on the state
on the state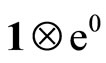 . Using
. Using 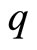 -conjugation and associativity properties, we explicitly construct in [3] the creative intertwining operators
-conjugation and associativity properties, we explicitly construct in [3] the creative intertwining operators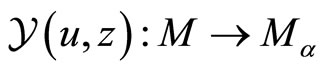 . We then prove:
. We then prove:
Theorem 1 (Tuite-Z) The creative intertwining operators 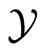 for
for 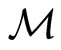 are generated by
are generated by  -conjugation of vertex operators of
-conjugation of vertex operators of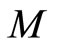 . For a Heisenberg state
. For a Heisenberg state![]() ,
,

The operators 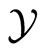 with some extra cocycle structure satisfy a natural extension from rational to complex parameters of the notion of a Generalized VOA as described by Dong and Lepowsky [7,12]. We then prove in [3].
with some extra cocycle structure satisfy a natural extension from rational to complex parameters of the notion of a Generalized VOA as described by Dong and Lepowsky [7,12]. We then prove in [3].
Theorem 2 (Tuite-Z)  satisfy the generalized Jacobi identity
satisfy the generalized Jacobi identity

for all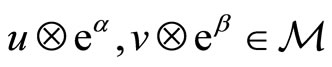 .
.
1.5. Invariant Form for the Extended Heisenberg Algebra
The definitions of invariant forms [8,13] for a VOSA and its ![]() -twisted modules were given by Scheithauer [14] and in [2] correspondingly. A bilinear form
-twisted modules were given by Scheithauer [14] and in [2] correspondingly. A bilinear form 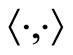 on
on  is said to be invariant if for all
is said to be invariant if for all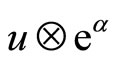 ,
, 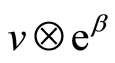 ,
, 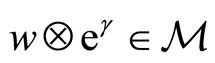 we have
we have

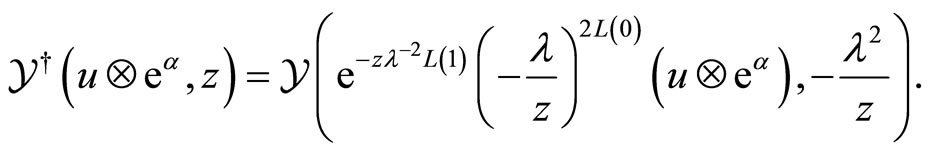
We are interested in the Möbius map 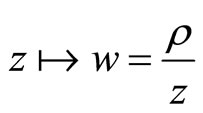
associated with the sewing condition so that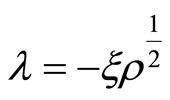 with
with . We prove in [3]
. We prove in [3]
Theorem 3 (Tuite-Z) The invariant form 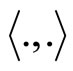 on
on  is symmetric, unique and invertible with
is symmetric, unique and invertible with
![]()
1.6. Rank Two Free Fermionic Vertex Operator Super Algebra
Consider the Vertex Operator Super Algebra (VOSA) generated by

for two vectors 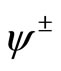 with modes satisfying anti-commutation relations
with modes satisfying anti-commutation relations

The VOSA vector space 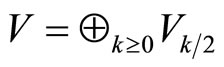 is a Fock space with basis vectors
is a Fock space with basis vectors

of weight
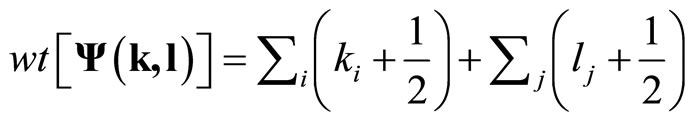 where
where 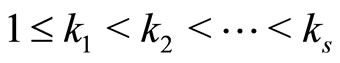 and
and  with
with 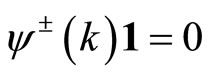 for all
for all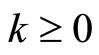 .
.
1.7. Rank Two Fermionic Vertex Operator Super Algebra
The conformal vector is

whose modes generate a Virasoro algebra of central charge 1. 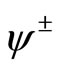 has
has  -weight
-weight![]() . The weight
. The weight 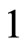 subspace of
subspace of 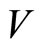 is
is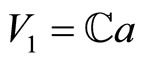 , for normalized Heisenberg bosonic vector
, for normalized Heisenberg bosonic vector , the conformal vector, and the Virasoro grading operator are
, the conformal vector, and the Virasoro grading operator are


2. Sewing of Riemann Surfaces
2.1. Basic Notions
For standard homology basis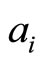 ,
, 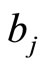 with
with 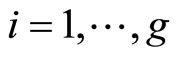 on a genus
on a genus ![]() Riemann surface [15,16] consider the normalized differential of the second kind which is a symmetric meromorphic form with
Riemann surface [15,16] consider the normalized differential of the second kind which is a symmetric meromorphic form with , has the form
, has the form

A normalized basis of holomorphic 1-forms![]() , the period matrix
, the period matrix![]() , and normalized differential of the third kind are given by
, and normalized differential of the third kind are given by
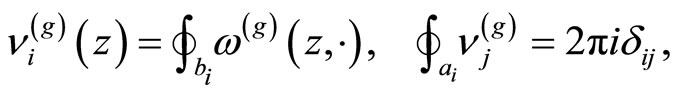

where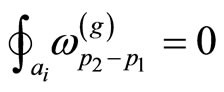 ,
,  for
for ,
,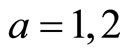 .
.
2.2. Period matrix
![]() is symmetric with positive imaginary part i.e.
is symmetric with positive imaginary part i.e. , the Siegel upper half plane. The canonical intersection form on cycles is preserved under the action of the symplectic group
, the Siegel upper half plane. The canonical intersection form on cycles is preserved under the action of the symplectic group 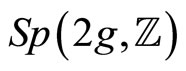 where
where
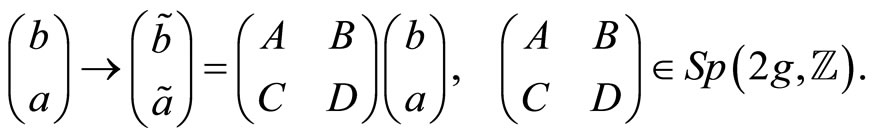
This induces the modular action on 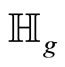

2.3. Sewing Two Tori to Form a Genus Two Riemann Surface
Consider 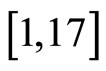 two oriented tori
two oriented tori ![]() with
with
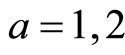 for
for  for
for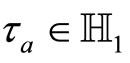 , the complex upper half plane. For
, the complex upper half plane. For 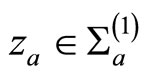 the closed disk
the closed disk
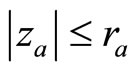 is contained in
is contained in  provided
provided 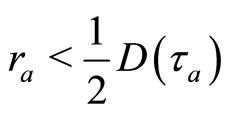
where
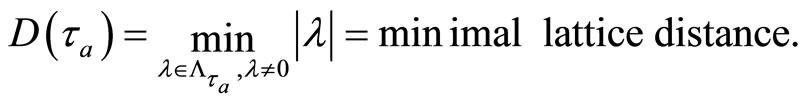
Introduce a sewing parameter 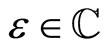 and excise the disks
and excise the disks  and
and 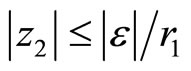 where
where
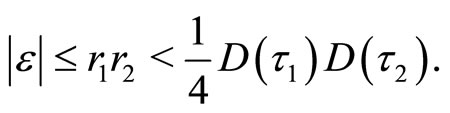
Identify the annular regions 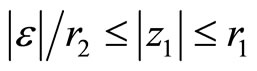 and
and 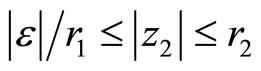 via the sewing relation
via the sewing relation
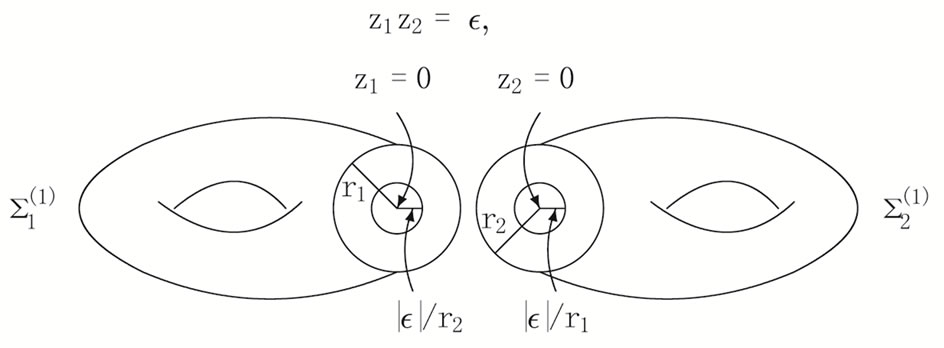
gives a genus two Riemann surface  parameterized by the domain
parameterized by the domain
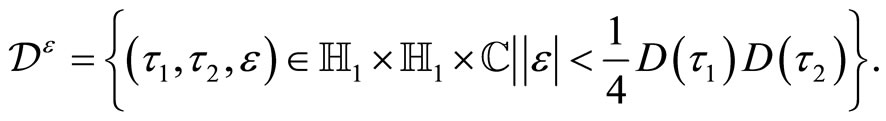
2.4. Torus Self-Sewing to Form a Genus Two Riemann Surface
In [1] we describe procedures of sewing Riemann surfaces [17]. Consider a self-sewing of the oriented torus ,
,  ,
,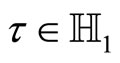 .
.
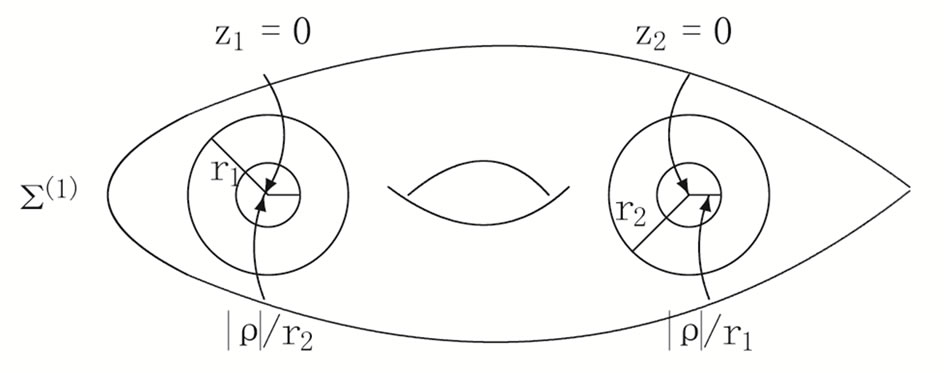
Define the annuli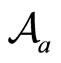 ,
,  centered at
centered at  and
and ![]() of
of 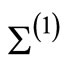 with local coordinates
with local coordinates  and
and  respectively. We use the convention
respectively. We use the convention ,
,
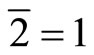 . Take the outer radius of
. Take the outer radius of 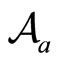 to be
to be
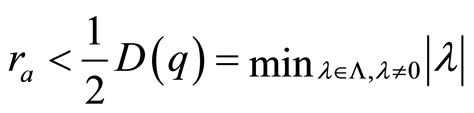 .
.
Introduce a complex parameter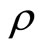 ,
,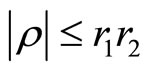 . Take inner radius to be
. Take inner radius to be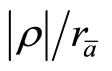 , with
, with .
.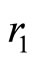 ,
, ![]() must be sufficiently small to ensure that the disks do not intersect. Excise the disks
must be sufficiently small to ensure that the disks do not intersect. Excise the disks
![]()
to form a twice-punctured surface
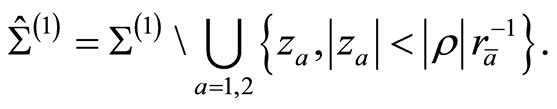
Identify the annular regions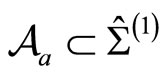 ,
,

as a single region  via the sewing relation
via the sewing relation

to form a compact genus two Riemann surface
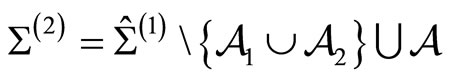 parameterized by
parameterized by

3. Elliptic Functions
3.1. Weierstrass Function
The Weierstrass 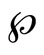 -function periodic in
-function periodic in 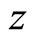 with periods
with periods 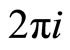 and
and  is
is
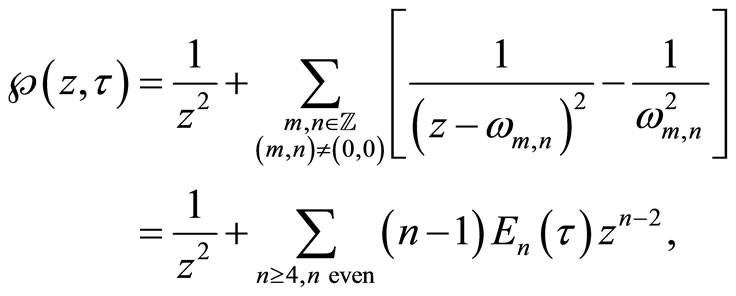
for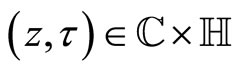 ,
,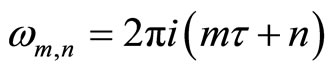 . We define for
. We define for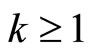 ,
,

Then
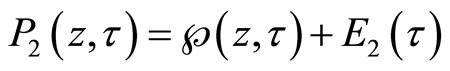 .
.
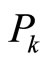 has periodicities
has periodicities

3.2. Eisenstein Series
The Eisenstein series 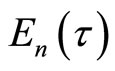 is equal to
is equal to  for
for ![]() odd, and for
odd, and for ![]()

where 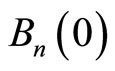 is the
is the ![]() th Bernoulli number. If
th Bernoulli number. If 
then 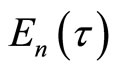 is a holomorphic modular form of weight
is a holomorphic modular form of weight ![]() on
on 

for all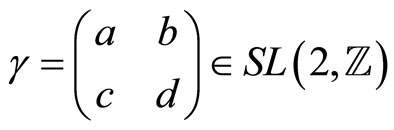 , where
, where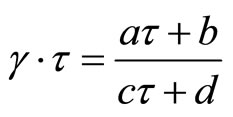 .
. 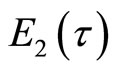 is a quasimodular form
is a quasimodular form
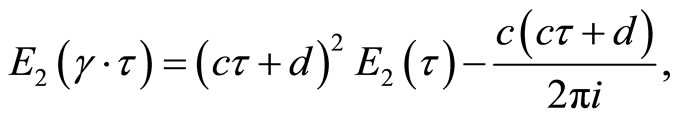
having the exceptional transformation law.
3.3. The Theta Function
We recall the definition of the theta function with real characteristics [18]
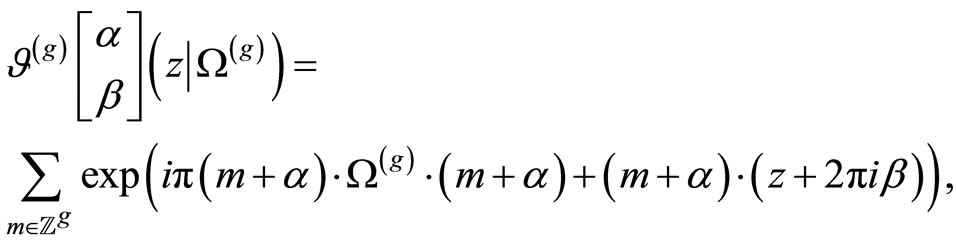
for
 ,
,
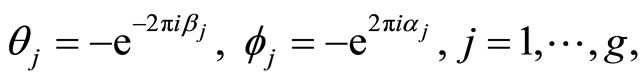
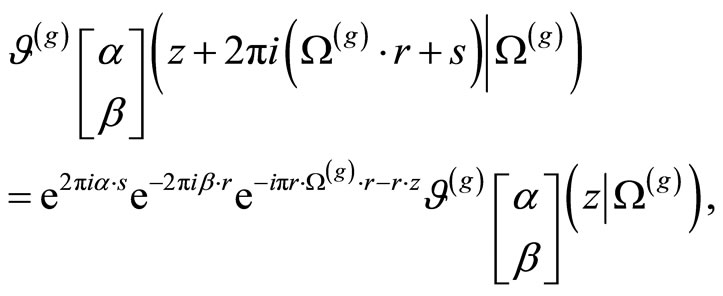
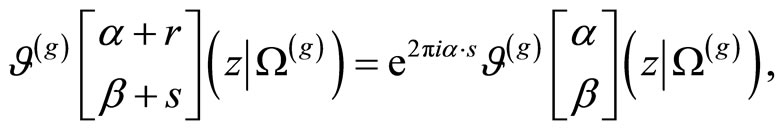
for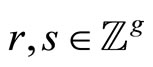 .
.
3.4. Twisted Elliptic Functions
Let 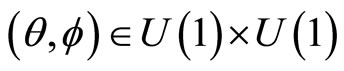 denote a pair of modulus one complex parameters with
denote a pair of modulus one complex parameters with 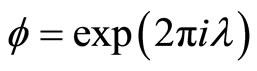 for
for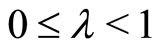 . For
. For 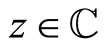 and
and  we define “twisted” Weierstrass functions for
we define “twisted” Weierstrass functions for  [19,20]
[19,20]
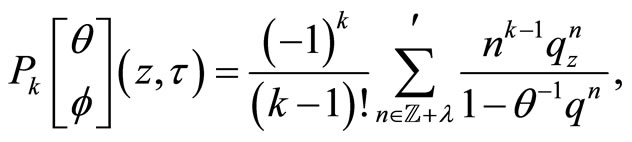
for  where
where  means we omit
means we omit 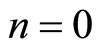 if
if
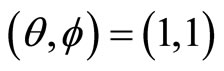 .
. 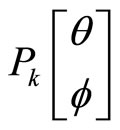
converges absolutely and uniformly on compact subsets of the domain  [20].
[20].
Lemma 1 (Mason-Tuite-Z) For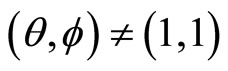 ,
,
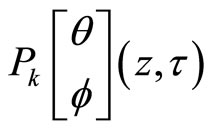
is periodic in 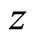 with periods
with periods  and
and  with multipliers
with multipliers  and
and  respectively.
respectively.
3.5. Modular Properties of Twisted Weierstrass Functions
Define the standard left action of the modular group for
 on
on 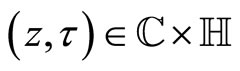 with
with

We also define a left action of ![]() on
on 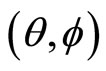

Then we obtain:
Theorem 4 (Mason-Tuite-Z) For 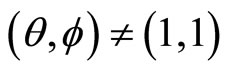 we have
we have

3.6. Twisted Eisenstein Series
We introduce twisted Eisenstein series for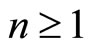 ,
,
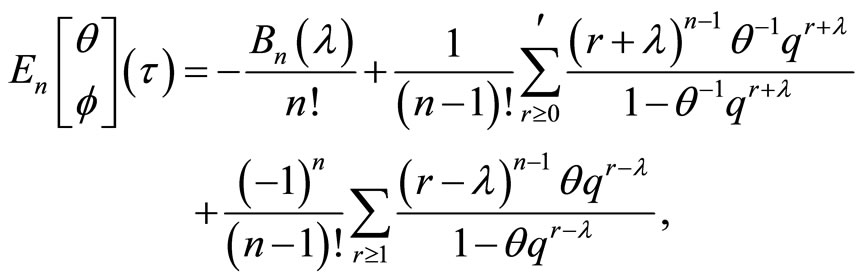
where  means we omit
means we omit  if
if 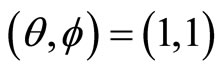 and where
and where  is the Bernoulli polynomial defined by
is the Bernoulli polynomial defined by

In particular
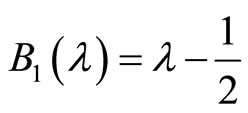 .
.
Note that
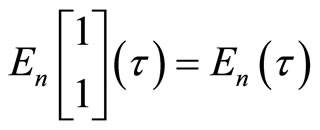 the standard Eisenstein series for even
the standard Eisenstein series for even , whereas
, whereas

for ![]() odd.
odd.
Theorem 5 (Mason-Tuite-Z) We have
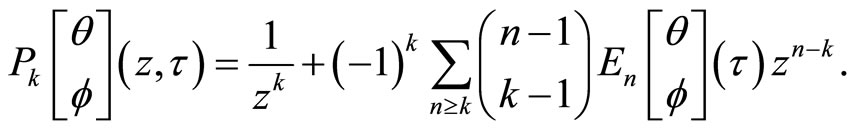
Theorem 6 (Mason-Tuite-Z) For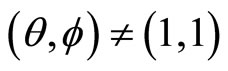 ,
,
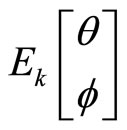 is a modular form of weight
is a modular form of weight 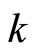 where
where
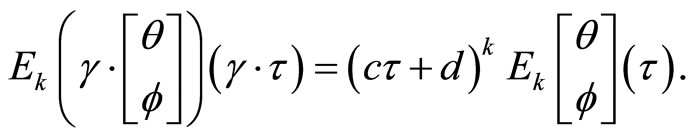
3.7. Twisted Elliptic Functions
In particular,

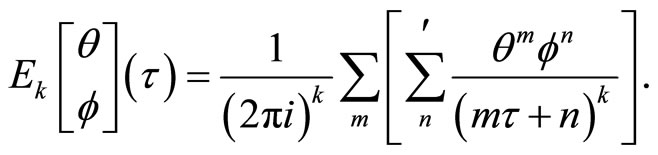
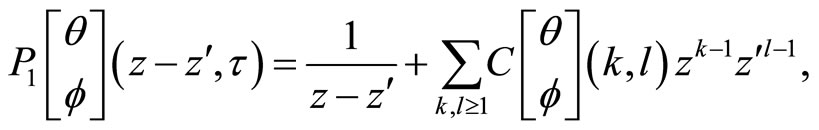
where
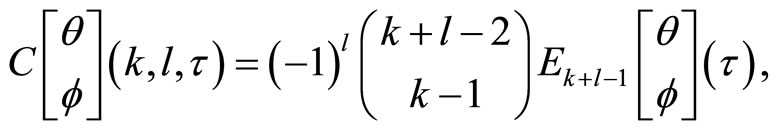
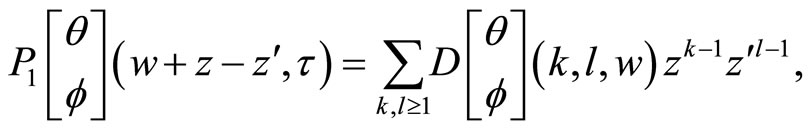
and
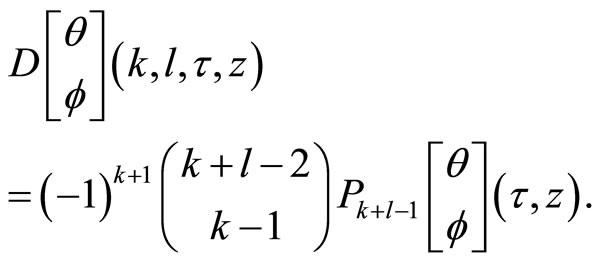
4. The Prime Form
There exists a (nonsingular and odd) character  such that [18,21,22]
such that [18,21,22]
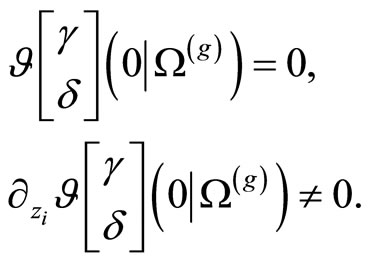
Let
 be a holomorphic 1-form, and let
be a holomorphic 1-form, and let 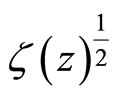 denote the form of weight
denote the form of weight ![]() on the double cover
on the double cover  of
of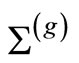 .
.
We define the prime form
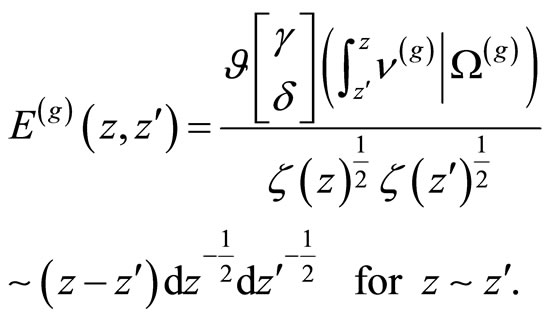
The prime form is anti-symmetic,
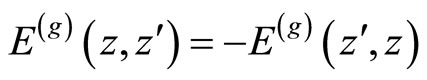 and a holomorphic differential form of weight
and a holomorphic differential form of weight
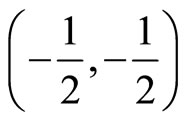 on
on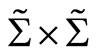 and has multipliers
and has multipliers  and
and 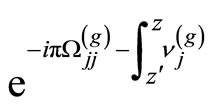 along the
along the 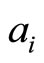
and 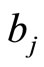 cycles in
cycles in 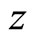 [21]. The normalized differentials of the second and third kind can be expressed in terms of the prime form [18]
[21]. The normalized differentials of the second and third kind can be expressed in terms of the prime form [18]

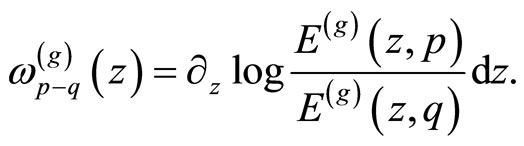
Conversely, we can also express the prime form in terms of 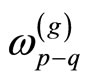 by [22]
by [22]
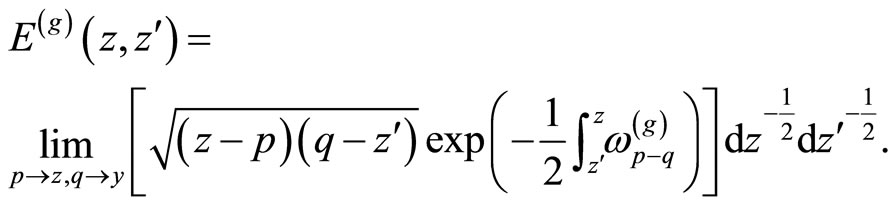
Torus Prime Form
The prime form on torus [18]

for  and
and  and where
and where
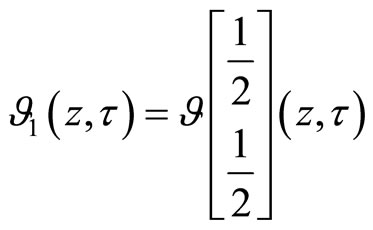 .
.
We have
![]()


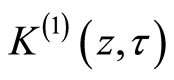 has periodicities
has periodicities


5. The Szegö Kernel
The Szegö Kernel [18,21,22] is defined by
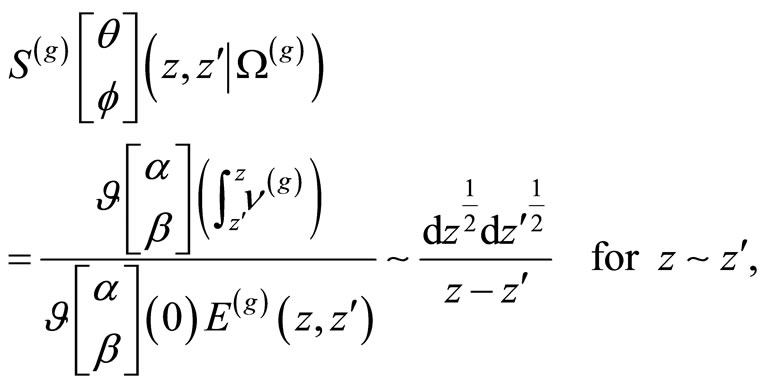
with ,
,  ,
, 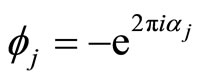 ,
,
 , where
, where 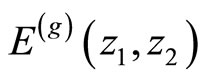 is the genus
is the genus ![]() prime form. The Szegö kernel has multipliers along the
prime form. The Szegö kernel has multipliers along the 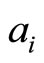 and
and 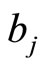 cycles in
cycles in  given by
given by  and
and  respectively and is a meromorphic
respectively and is a meromorphic  -form on
-form on 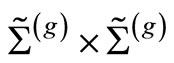
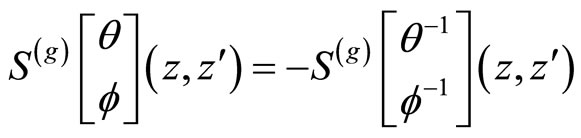
where  and
and .
.
Finally, we describe the modular invariance of the Szegö kernel under the symplectic group 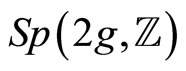 where we find [21]
where we find [21]

with![]() ,
, 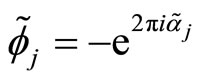 ,
,
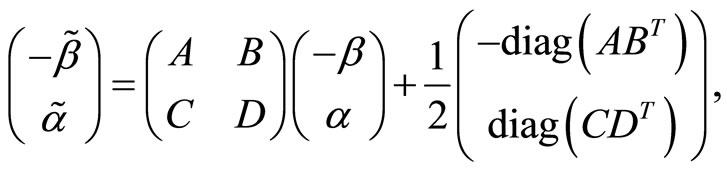

where  denotes the diagonal elements of a matrix
denotes the diagonal elements of a matrix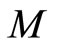 .
.
5.1. Modular Properties of the Szegö Kernel
Finally, we describe the modular invariance of the Szegö kernel under the symplectic group 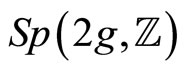 where we find [21]
where we find [21]
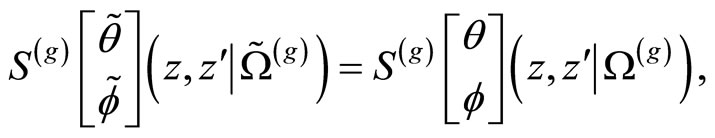
where![]() ,
, 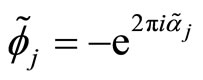 for
for
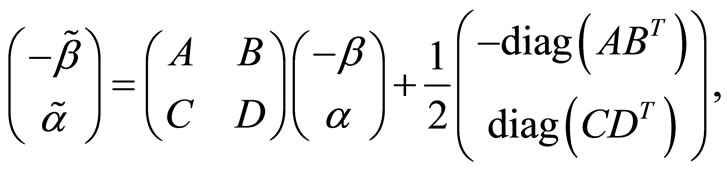
where  denotes the diagonal elements of a matrix
denotes the diagonal elements of a matrix .
.
5.2. Torus Szegö Kernel
On the torus  the Szegö kernel for
the Szegö kernel for  is
is
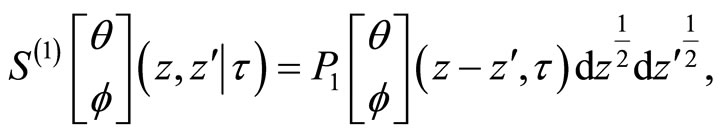
where
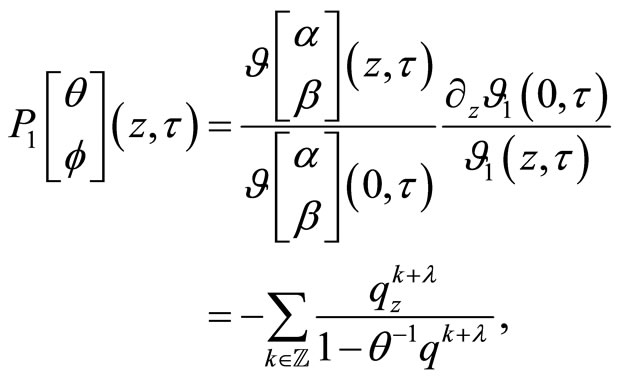
for
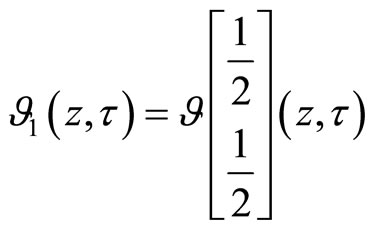 ,
, 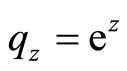 and
and
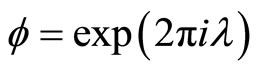 for
for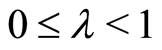 .
.
6. Structures on 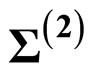 Constructed from Genus One Data
Constructed from Genus One Data
Yamada (1980) described how to compute the period matrix and other structures on a genus ![]() Riemann surface in terms of lower genus data.
Riemann surface in terms of lower genus data.
6.1. 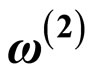 on the Sewn Surface
on the Sewn Surface 
 can be determined from
can be determined from 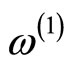 on each torus in Yamada’s sewing scheme [17,23]. For a torus
on each torus in Yamada’s sewing scheme [17,23]. For a torus 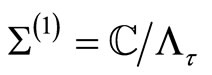 the differential is
the differential is
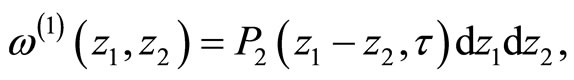
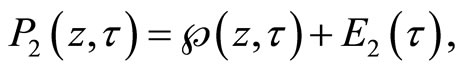
for Weierstrass function
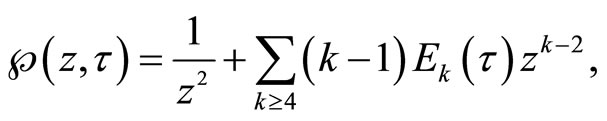
and Eisenstein series for 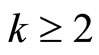

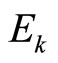 vanishes for odd
vanishes for odd  and is a weight
and is a weight 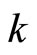 modular form for
modular form for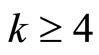 .
. 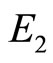 is a quasi-modular form. Expanding
is a quasi-modular form. Expanding
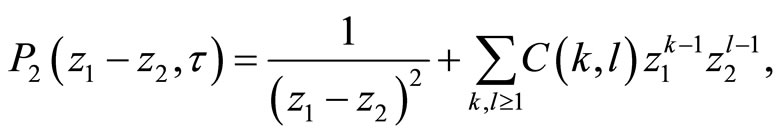

we compute 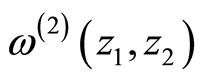 in the sewing scheme in terms of the following genus one data,
in the sewing scheme in terms of the following genus one data, 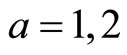

6.2. A Determinant and the Period Matrix
Consider the infinite matrix  where
where 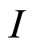 is the infinite identity matrix and define
is the infinite identity matrix and define 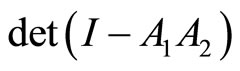 by
by
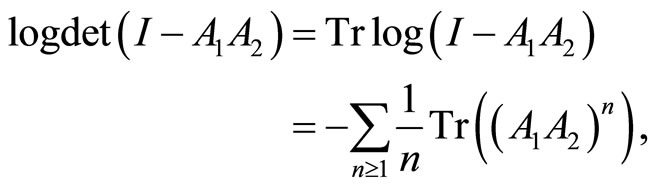
as a formal power series in ![]() [23].
[23].
Theorem 7 (Mason-Tuite)
a) The infinite matrix
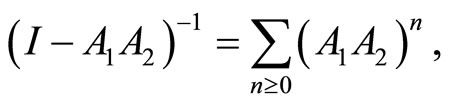
is convergent for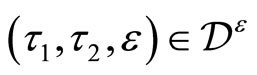 .
.
b)  is non-vanishing and holomorphic on
is non-vanishing and holomorphic on .
.
Furthermore we may obtain an explicit formula for the genus two period matrix 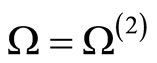 on
on  [23].
[23].
Theorem 8 (Mason-Tuite)  is holomorphic on
is holomorphic on 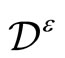 and is given by
and is given by
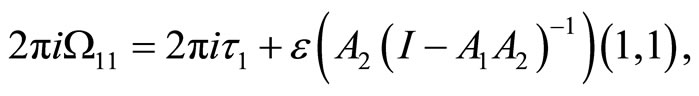
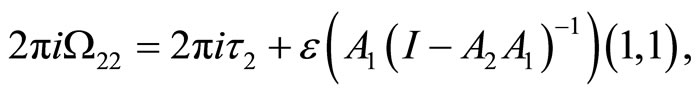
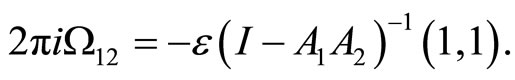
Here 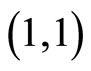 refers to the
refers to the 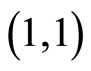 -entry of a matrix.
-entry of a matrix.
6.3. Genus Two Szegö Kernel on 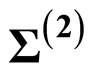 in the
in the 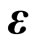 -Formalism
-Formalism
We may compute 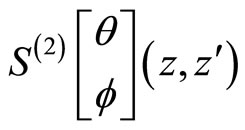 for
for 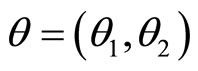 in the sewing scheme in terms of the genus one data
in the sewing scheme in terms of the genus one data

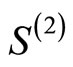 is described in terms of the infinite matrix
is described in terms of the infinite matrix 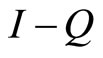 for
for
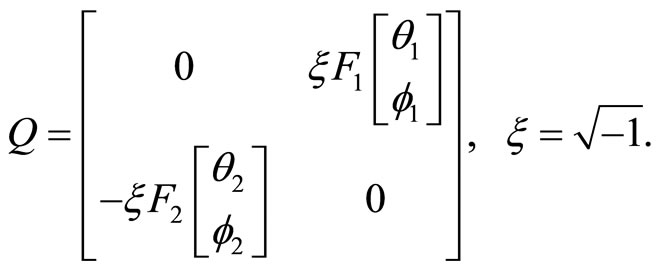
Theorem 9 (Tuite-Z)
a) The infinite matrix 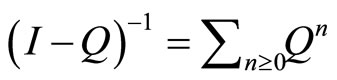 is convergent for
is convergent for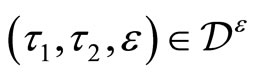 b)
b) 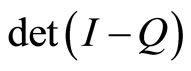 is non-vanishing and holomorphic on
is non-vanishing and holomorphic on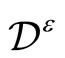 .
.
6.4. Genus Two Szegö Kernel in the 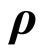 -Formalism
-Formalism
It is convenient to define 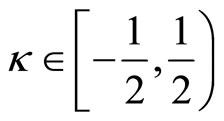 by
by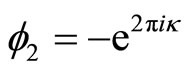 .
.
Then we prove [1] the following Theorem 10 (Tuite-Z) 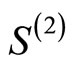 is holomorphic in
is holomorphic in 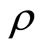 for
for 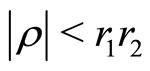 with
with

for 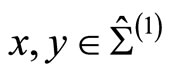 where
where 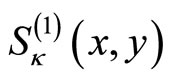 is defined for
is defined for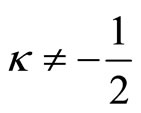 , by
, by

with similar expression for 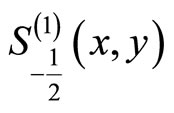 for
for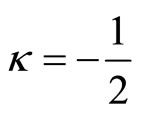 .
.
Let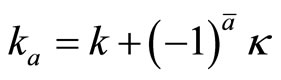 , for
, for  and integer
and integer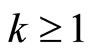 . We introduce the moments for
. We introduce the moments for :
:
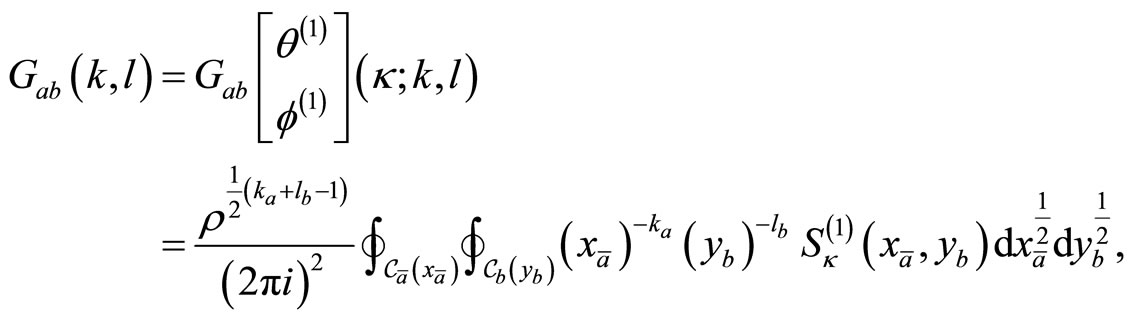
with associated infinite matrix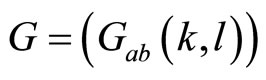 . We define also half-order differentials
. We define also half-order differentials

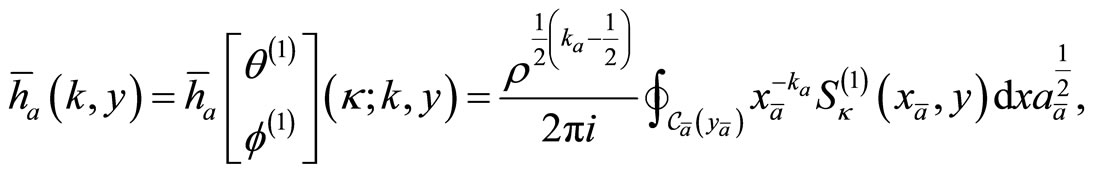
and let  and
and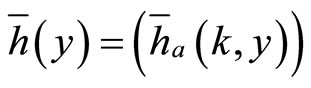 , denote the infinite row vectors indexed by
, denote the infinite row vectors indexed by![]() ,
,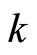 . From the sewing relation
. From the sewing relation 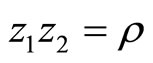 we have
we have
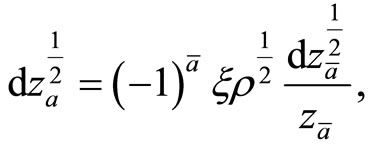
for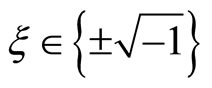 , depending on the branch of the double cover of
, depending on the branch of the double cover of  chosen. It is convenient to define
chosen. It is convenient to define

with an infinite diagonal matrix
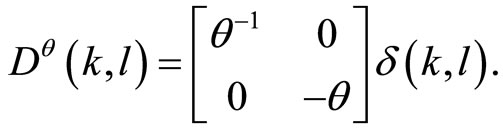
Defining 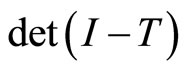 by the formal power series in
by the formal power series in 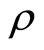
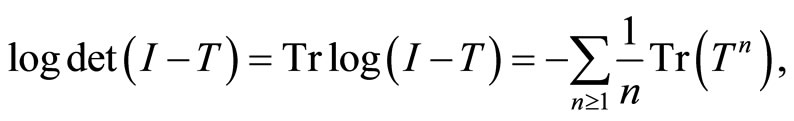
we prove in [1].
Theorem 11 (Tuite-Z)
a)  is convergent for
is convergent for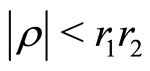 b)
b) 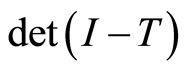 is non-vanishing and holomorphic in
is non-vanishing and holomorphic in  on
on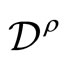 .
.
Theorem 12 (Tuite-Z) 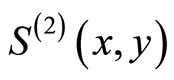 is given by
is given by
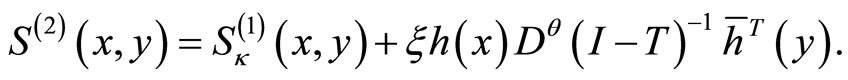
7. Genus One Partition and n-Point Functions
7.1. The Torus Partition Function for a Heisenberg VOA
For a VOA  of central charge
of central charge ![]() define the genus one partition (trace or characteristic) function by
define the genus one partition (trace or characteristic) function by

for the Heisenberg VOA  commutation relations with modes
commutation relations with modes
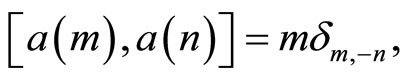

7.2. Genus One Twisted Graded Dimension
We define the genus one partition function for the VOSA by the supertrace

where .
.
More generally, we can construct a  -twisted module
-twisted module 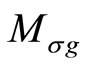 for any automorphism
for any automorphism 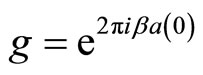 generated by the Heisenberg state
generated by the Heisenberg state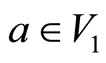 . We introduce the second automorphism
. We introduce the second automorphism 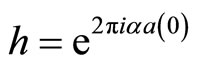 and define the orbifold
and define the orbifold  -twisted trace by
-twisted trace by
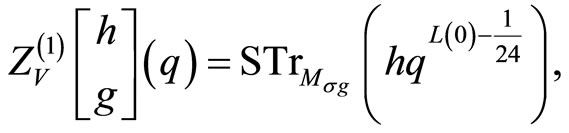
to find for ,
,

7.3. Genus One Fermionic One-Point Functions
Each orbifold 1-point function can found from a generalized Zhu reduction formulas as a determinant.
Theorem 13 (Mason-Tuite-Z) For a Fock vector

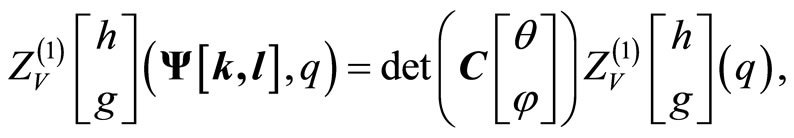
where for 

7.4. Genus One n-Point Functions for VOA
In general, we can define the genus one orbifold n-point function for  by
by
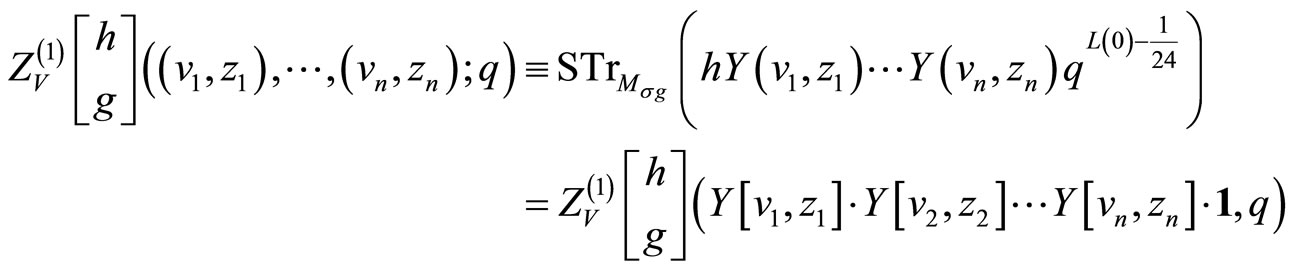
Every orbifold n-point function can be computed using generalized Zhu reduction formulas in terms of a determinant with entries arising from the basic 2-point function for 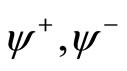 [19].
[19].
7.5. Zhu Reduction Formula
To reduce an  -point function to a sum of
-point function to a sum of ![]() -point functions we need:
-point functions we need:
The supertrace property

Borcherds commutation formula:
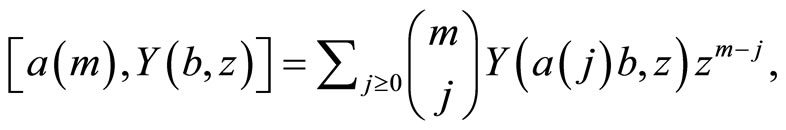
expansions for  -functions:
-functions:


Theorem 14 (Mason-Tuite-Z) For any  we have
we have
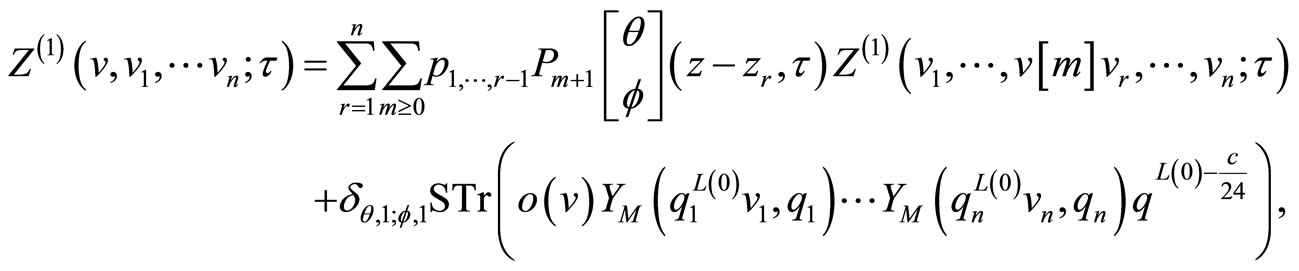
where 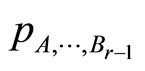 is given by
is given by

7.6. General Genus One Fermionic n-Point Functions
The generating two-point function (for ) is given by
) is given by

Theorem 15 (Mason-Tuite-Z)
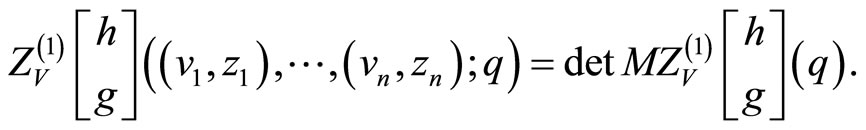
Theorem 16 (Mason-Tuite-Z) For ![]() Fock vectors
Fock vectors

and
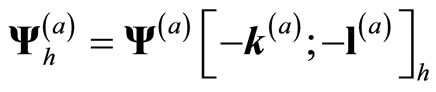
for ![]() and
and ![]() with
with
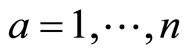 . Then for
. Then for 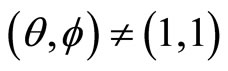 the corresponding
the corresponding ![]() -point functions are non-vanishing provided
-point functions are non-vanishing provided
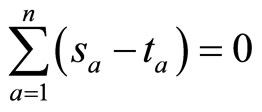 and
and
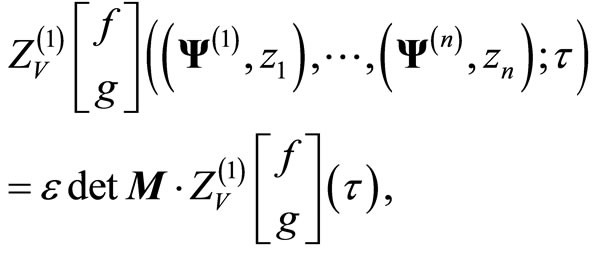
where ![]() is certain parity factor. Here
is certain parity factor. Here  is the block matrix
is the block matrix
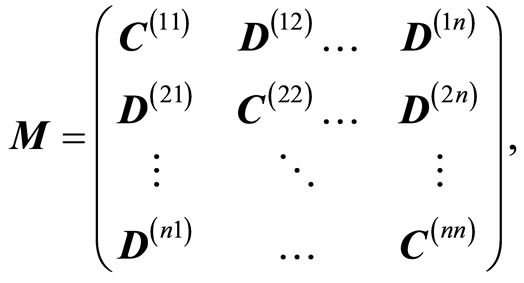
with

for 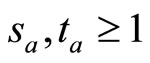 with
with  and
and

for 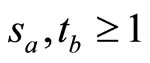 with
with 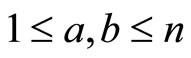 and
and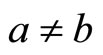 .
. ![]() is the sign of the permutation associated with the reordering of
is the sign of the permutation associated with the reordering of 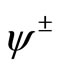 to the alternating ordering.
to the alternating ordering.
Furthermore, the ![]() -point function is an analytic function in
-point function is an analytic function in  and converges absolutely and uniformly on compact subsets of the domain
and converges absolutely and uniformly on compact subsets of the domain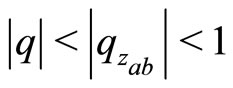 .
.
7.7. Torus Intertwined n-Point Functions
As in ordinary (non-intertwined) case [2,19,20,24-29] we construct in [4] the partition and ![]() -point functions [30-39] for vertex operator algebra modules.
-point functions [30-39] for vertex operator algebra modules.
Let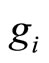 ,
, 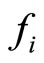 ,
, 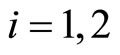 be VOSA
be VOSA  automorphisms commuting with
automorphisms commuting with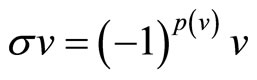 . For
. For 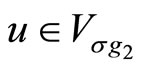 and the states
and the states 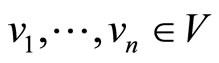 we define the intertwined
we define the intertwined ![]() -point function [4] on the torus by
-point function [4] on the torus by
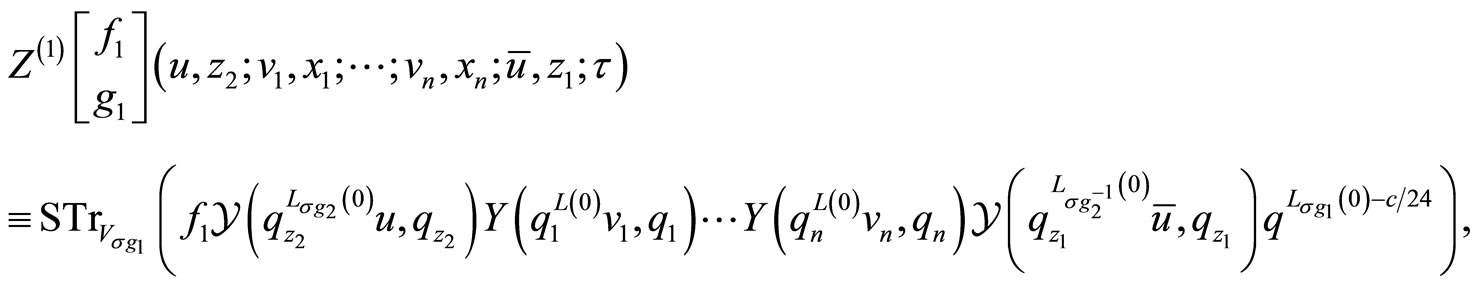
where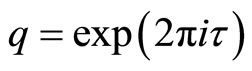 ,
,  ,
, ![]() ,
,
 ;
; , for variables
, for variables 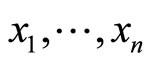 associated to the local coordinates on the torus, and
associated to the local coordinates on the torus, and ![]() is dual for
is dual for ![]() with respect to the invariant form on
with respect to the invariant form on![]() . The supertrace over a
. The supertrace over a  -module
-module  is defined by
is defined by
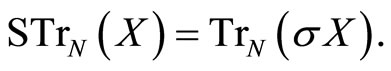
For an element  of a VOSA
of a VOSA ![]() -twisted
-twisted 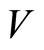 -module we introduce also the differential form
-module we introduce also the differential form

associated to the torus intertwined ![]() -point function.
-point function.
7.8. Torus Intertwined Two-Point Function
The rank two free fermionic VOSA , [10]
, [10]
is generated by 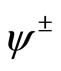 with
with
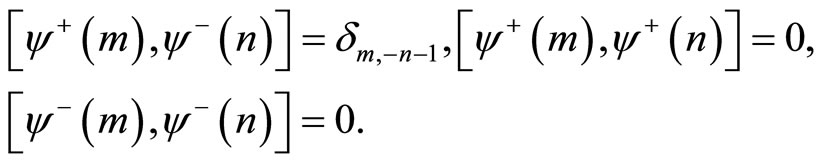
The rank two free fermion VOSA intertwined torus
![]() -point function is parameterized by
-point function is parameterized by ,
,  , and
, and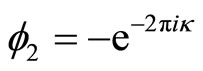 , [2, 4] where
, [2, 4] where
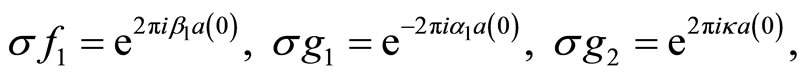
for real valued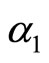 ,
,  ,
, ![]() ,
,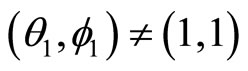 .
.
For 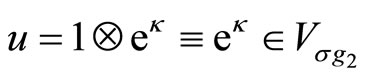 and
and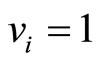 ,
, 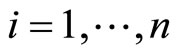
we obtain [4] the basic intertwined two-point function on the torus
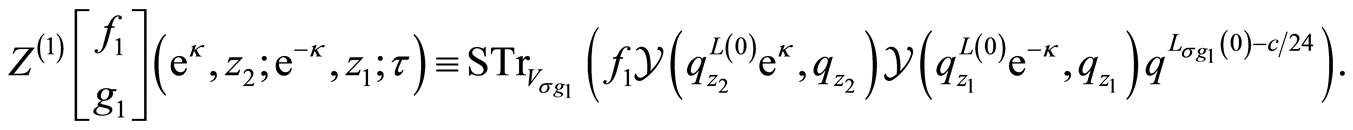
We then consider the differential form
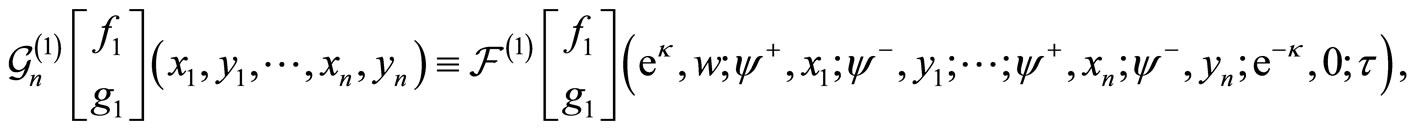
associated to the torus intertwined  -point function
-point function
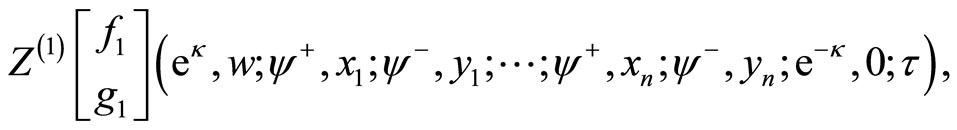
with alternatively inserted ![]() states
states 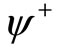 and
and ![]() states
states 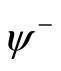 distributed on the resulting genus two Riemann surface
distributed on the resulting genus two Riemann surface 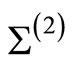 at points
at points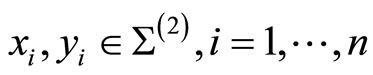 . We then prove in [4].
. We then prove in [4].
Theorem 17 (Tuite-Z) For the rank two free fermion vertex operator superalgebra 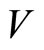 and for
and for 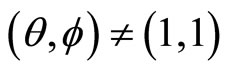 the generating form is given by
the generating form is given by
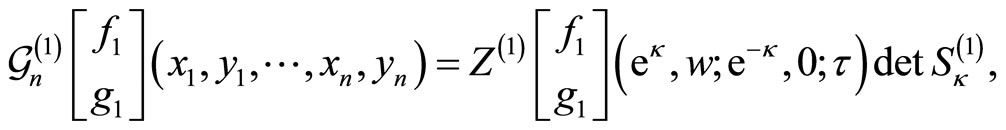
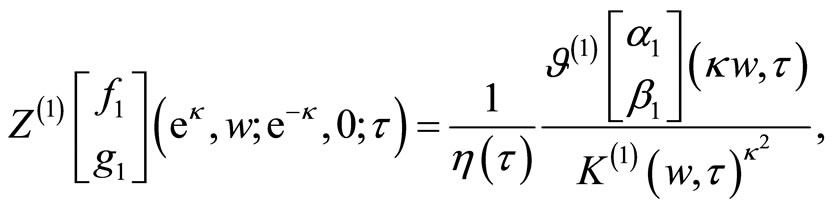
is the basic intertwined two-point function on the torus, and ![]() -matrix
-matrix
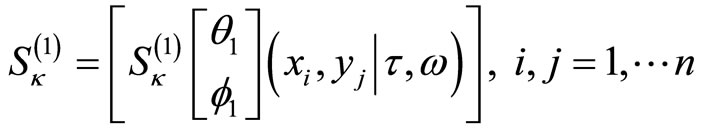 with elements given by parts of the Szegö kernel.
with elements given by parts of the Szegö kernel.
8. Genus Two Partition and n-Point Functions
8.1. Genus Two Partition Function in 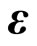 -Formalism
-Formalism
We define the genus two partition function in the earlier sewing scheme in terms of data coming from the two tori, namely the set of 1-point functions 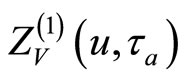 for all
for all . We assume that
. We assume that 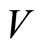 has a nondegenerate invariant bilinear form—the Li-Zamolodchikov metric. Define
has a nondegenerate invariant bilinear form—the Li-Zamolodchikov metric. Define
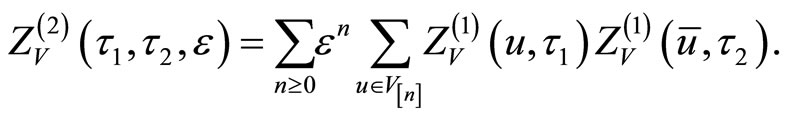
The inner sum is taken over any basis and ![]() is dual to
is dual to ![]() wrt to the Li-Zamolodchikov metric.
wrt to the Li-Zamolodchikov metric.
8.2. Genus Two Partition Function for the Heisenberg VOA
We can compute  using a combinatorial-graphical technique based on the explicit Fock basis and recalling the infinite matrices
using a combinatorial-graphical technique based on the explicit Fock basis and recalling the infinite matrices .
.
Theorem 18 (Mason-Tuite) a) The genus two partition function for the rank one Heisenberg VOA is
 ;
;
b)  is holomorphic on the domain
is holomorphic on the domain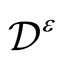 ;
;
c) 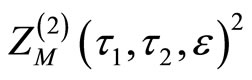 is automorphic of weight
is automorphic of weight ;
;
d) 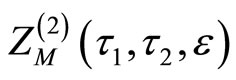 has an infinite product formula.
has an infinite product formula.
8.3. Genus Two Fermionic Partition Function
Following the definition for the bosonic VOA we define for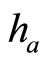 ,
, 
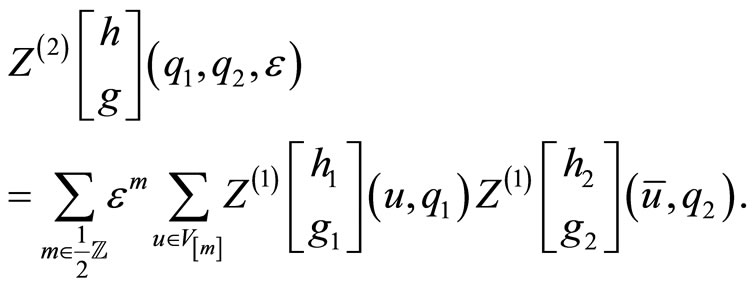
The inner sum is taken over any 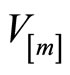 basis and
basis and ![]() is dual to
is dual to ![]() with respect to the Li-Zamolodchikov square bracket metric.
with respect to the Li-Zamolodchikov square bracket metric. 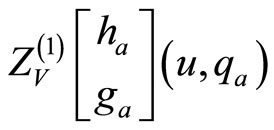 is the genus one orbifold 1-point function. Recall that the non-zero 1-point functions arise for Fock vectors
is the genus one orbifold 1-point function. Recall that the non-zero 1-point functions arise for Fock vectors
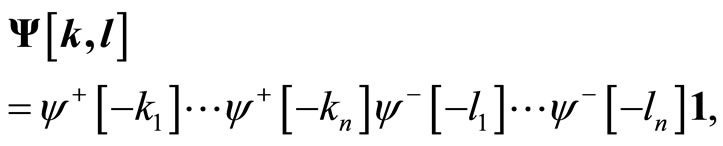
such that
 ,
,

The Li-Zamolodchikov metric dual to the Fock vector is

Recalling the infinite matrix  we find
we find
Theorem 19 (Tuite-Z)
a) The genus two orbifold partition function is
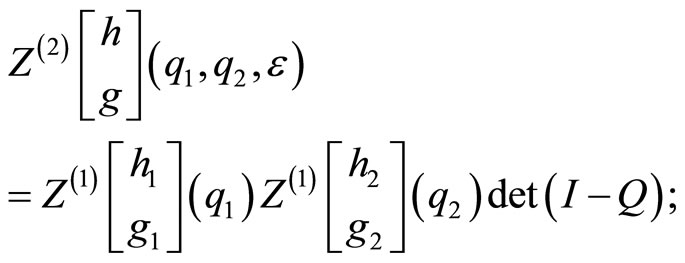
b) 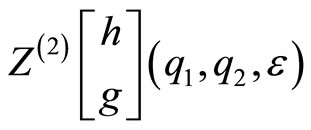 is holomorphic on the domain
is holomorphic on the domain ;
;
c) 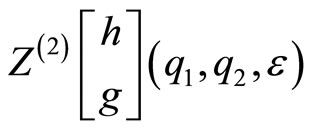 has natural modular properties under the action of
has natural modular properties under the action of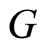 .
.
8.4. Genus Two Partition and ![]() -Point Functions in
-Point Functions in 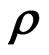 -Formalism
-Formalism
Let  be automorphisms, and
be automorphisms, and ![]() be twisted
be twisted 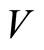 -modules of a vertex operator superalgebra
-modules of a vertex operator superalgebra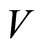 . For
. For
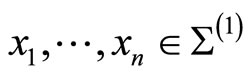 with
with  and
and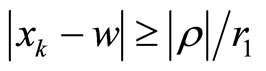 ,
,
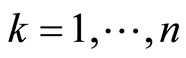 , we define the genus two
, we define the genus two ![]() -point function [4] in the
-point function [4] in the 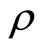 -formalism by
-formalism by
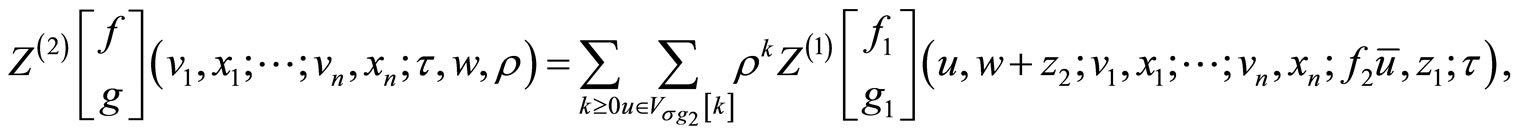
where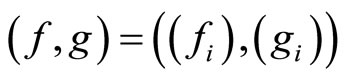 , where
, where 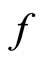 (respectively
(respectively![]() )
)
denotes the pair ,
, 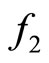 (respectively
(respectively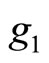 ,
,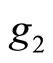 ). The sum is taken over any
). The sum is taken over any ![]() -basis.
-basis.
In particular, we introduce the genus two partition function

where 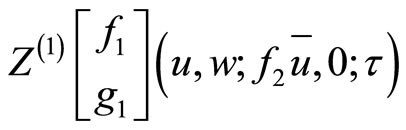 is the genus one intertwined two point function.
is the genus one intertwined two point function.
Remark 1 We can generalize the genus two ![]() -point function by introducing and computing the differential form associated to the torus
-point function by introducing and computing the differential form associated to the torus ![]() -point function containing several intertwining operators in the supertrace as well as corresponding genus two
-point function containing several intertwining operators in the supertrace as well as corresponding genus two ![]() -point functions.
-point functions.
Similar to the ordinary genus two case [2], we define the differential form [4] associated to the ![]() -point function on a sewn genus two Riemann surface for
-point function on a sewn genus two Riemann surface for  and
and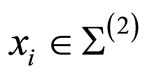 ,
, 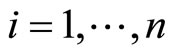 with
with
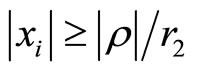 ,
, 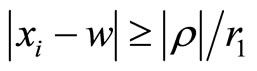 ,
,
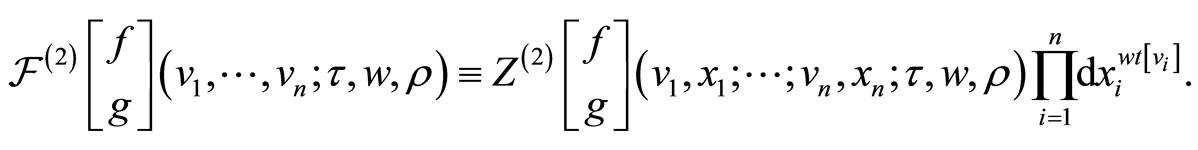
9. Generalizations of Classical Identities
9.1. Bosonization
The genus one orbifold partition function can be alternatively computed by decomposing the VOSA into Heisenberg modules 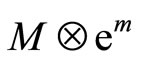 indexed by
indexed by 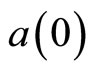 integer eigenvalues
integer eigenvalues![]() , i.e., a
, i.e., a 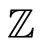 lattice [26]. Let
lattice [26]. Let 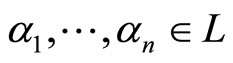 be lattice elements of the rank one even lattice,
be lattice elements of the rank one even lattice, 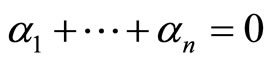 , and
, and 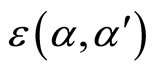 -cocycle. Then
-cocycle. Then
Theorem 20 (Tuite-Mason)
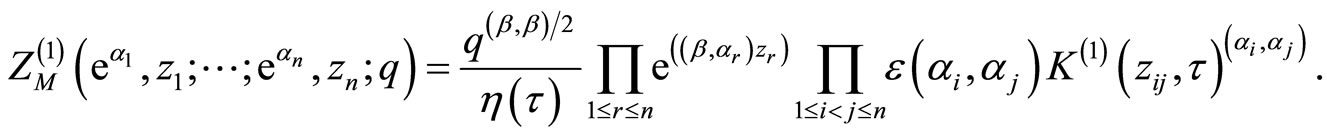
Then ther genus one twisted partition function is given by
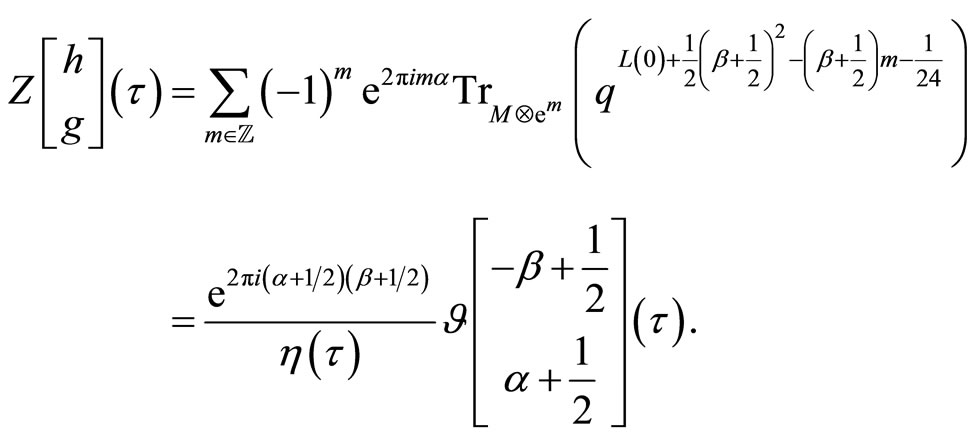
Comparing to the fermionic product formula we obtain the classical Jacobi triple product formula:
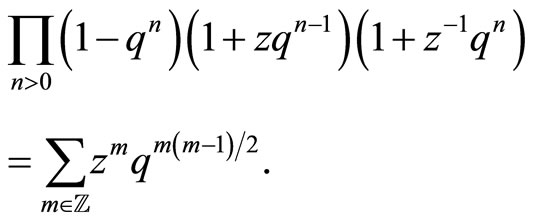
9.2. Genus Two Jacobi Triple Product Formula
The genus two partition function can similarly be computed in the bosonized formalism to obtain a genus two version of the Jacobi triple product formula for the genus two Riemann theta function [19]
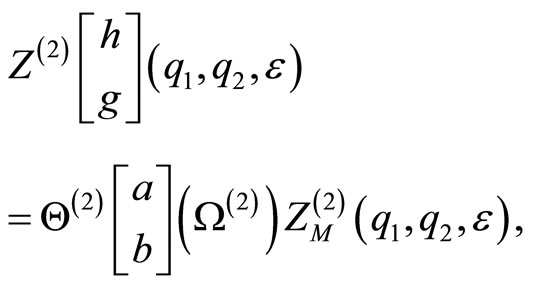
for an appropriate character valued genus two Riemann theta function
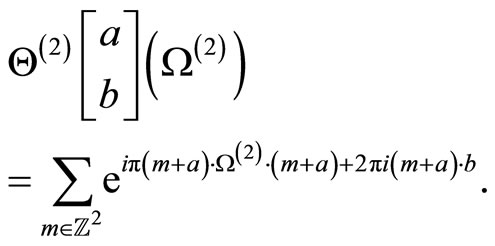
Comparing with the fermionic result we thus find that on 
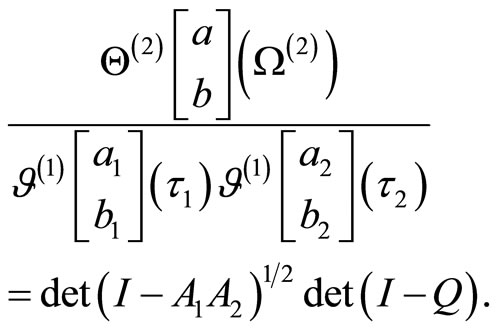
9.3. Fay’s Trisecant Identity
Recall Fay’s trisecant identity [21]
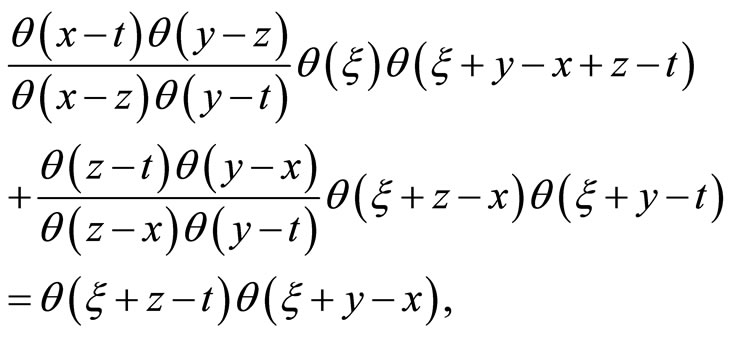
for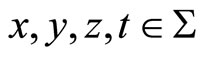 ,
, 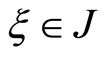 , where
, where ![]() is the Jacobian of the curve.
is the Jacobian of the curve.
9.4. Bosonized Generating Function and Trisecant Identity
In a similar fashion we can compute the general 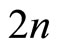 - generating function
- generating function 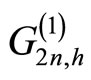 in the bosonic setting to obtain:
in the bosonic setting to obtain:
Theorem 21 (Mason-Tuite-Z)

Comparing this to fermionic expressions for  we obtain the classical Frobenius elliptic function version of generalized Fay’s trisecant identity
we obtain the classical Frobenius elliptic function version of generalized Fay’s trisecant identity
[21]:
Corollary 1 (Mason-Tuite-Z) For 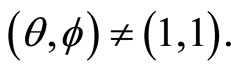 we have
we have
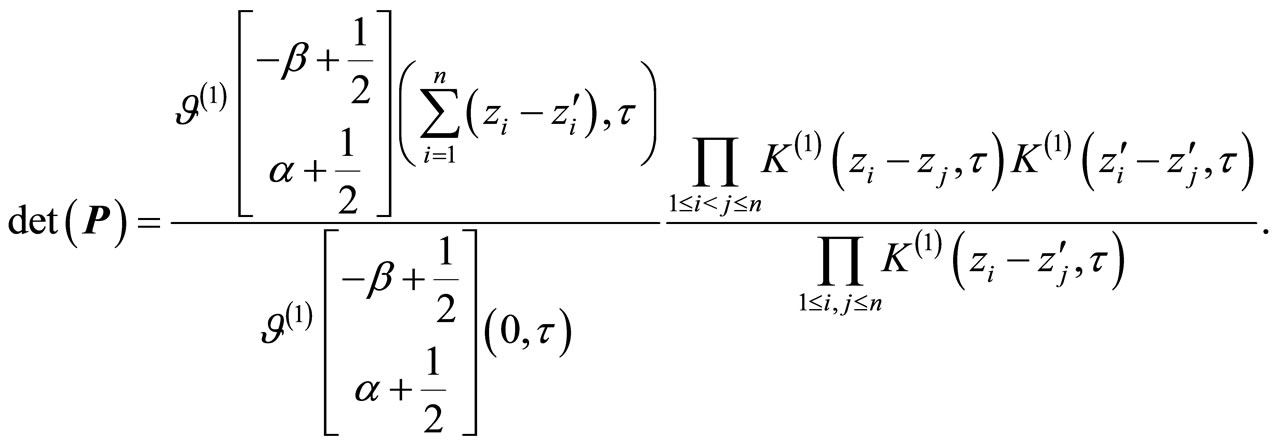
9.5. Generalized Fay’s Trisecant Identity
We may generalize these identities using [26]. Consider the general lattice ![]() -point function. We have [19], For integers
-point function. We have [19], For integers 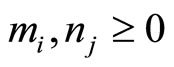 satisfying
satisfying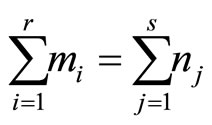 , we have
, we have


Comparing this to the expression for ![]() -point functions we obtain a new elliptic generalization of Fay’s trisecant identity:
-point functions we obtain a new elliptic generalization of Fay’s trisecant identity:
Corollary 2 (Mason-Tuite-Z) For 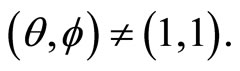 we have
we have

Here 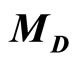 is the block matrix
is the block matrix

with  the
the 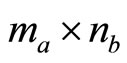 matrix
matrix
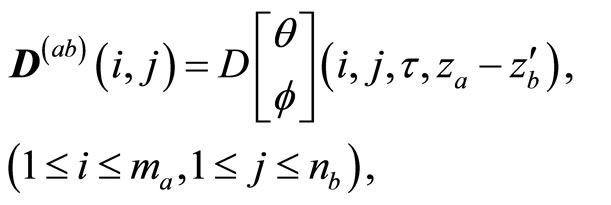
for  and
and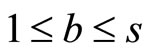 , and
, and 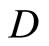 -functions are given by the expansion
-functions are given by the expansion

10. Genus Two Intertwined Partition and n-Point Functions
In [4] we then prove:
Theorem 22 (Tuite-Z) Let 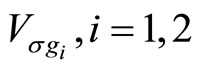 be
be 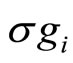 twisted
twisted  -modules for the rank two free fermion vertex operator superalgebra
-modules for the rank two free fermion vertex operator superalgebra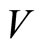 . Let
. Let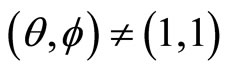 . Then the partition function on a genus two Riemann surface obtained in the
. Then the partition function on a genus two Riemann surface obtained in the 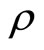 -self-sewing formalism of the torus is a non-vanishing holomorphic function on
-self-sewing formalism of the torus is a non-vanishing holomorphic function on 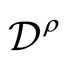 given by
given by
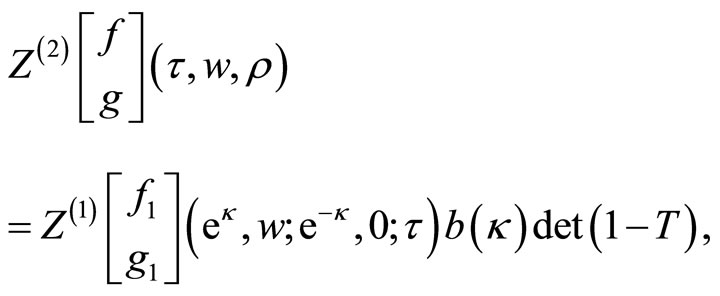
where 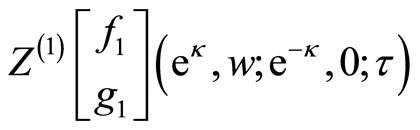 is the intertwined
is the intertwined 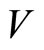 module
module 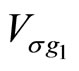 torus basic two-point function, and
torus basic two-point function, and  is some function.
is some function.
We may similarly compute the genus two partition function in the  -formalism for the original rank one fermion VOSA
-formalism for the original rank one fermion VOSA  in which case we can only construct a
in which case we can only construct a ![]() -twisted module. Then we have [4] the following:
-twisted module. Then we have [4] the following:
Corollary 3 (Tuite-Z) Let  be the rank one free fermion vertex operator superalgebra and
be the rank one free fermion vertex operator superalgebra and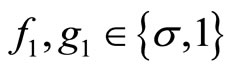 ,
, 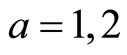 , be automorphisms. Then the partition function for
, be automorphisms. Then the partition function for 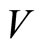 -module
-module  on a genus two Riemann surface obtained from
on a genus two Riemann surface obtained from  formalism of a self-sewn torus
formalism of a self-sewn torus  is given by
is given by
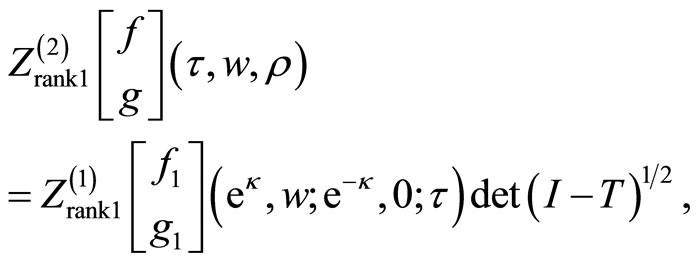
where 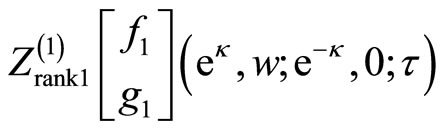 is the rank one fermion intertwined partition function on the original torus.
is the rank one fermion intertwined partition function on the original torus.
10.1. Genus Two Generating Form
In [4] we define matrices


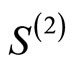 and
and 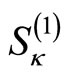 are finite matrices indexed by
are finite matrices indexed by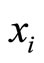 ,
, 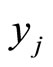 for
for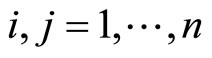 ;
; 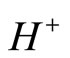 is semi-infinite with
is semi-infinite with ![]() rows indexed by
rows indexed by 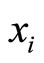 and columns indexed by
and columns indexed by 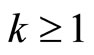 and
and 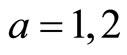 and
and  is semi-infinite with rows indexed by
is semi-infinite with rows indexed by ![]() and
and  and with
and with ![]() columns indexed by
columns indexed by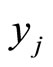 . We then prove
. We then prove
Lemma 2 (Tuite-Z)

with![]() ,
,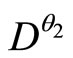 .
.
Introduce the differential form
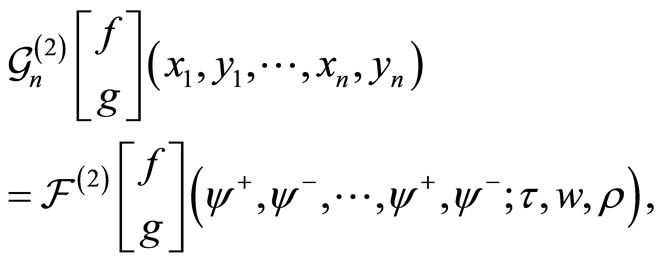
associated to the rank two free fermion VOSA genus two 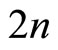 -point function
-point function
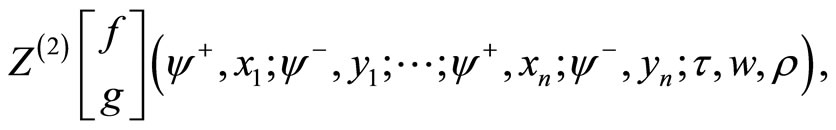
with alternatively inserted ![]() states
states 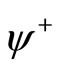 and
and ![]() states
states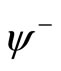 . The states are distributed on the genus two Riemann surface
. The states are distributed on the genus two Riemann surface 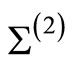 at points
at points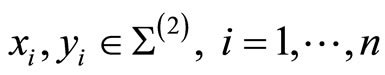 . Then we have Theorem 23 (Tuite-Z) All
. Then we have Theorem 23 (Tuite-Z) All ![]() -point functions for rank two free fermion VOSA twisted modules
-point functions for rank two free fermion VOSA twisted modules  on self-sewn torus are generated by the differential form
on self-sewn torus are generated by the differential form
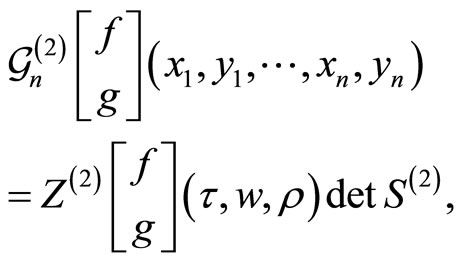
where the elements of the matrix

and 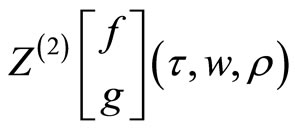 is the genus two partition function.
is the genus two partition function.
10.2. Modular Invariance Properties of Intertwined Functions
Following the ordinary case [20,27,40] we would like to describe modular properties of genus two “intertwined” partition and ![]() -point generating functions. As in [27], consider
-point generating functions. As in [27], consider 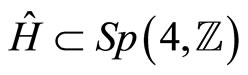 with elements
with elements

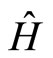 is generated by
is generated by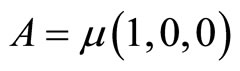 ,
, 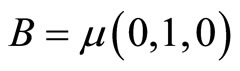 and
and  with relations
with relations
 .
.
We also define  where
where 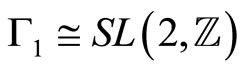 with elements
with elements
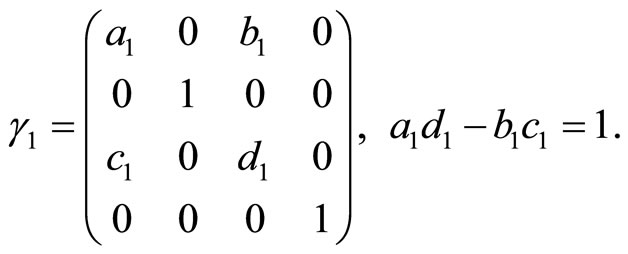
Together these groups generate
 .
.
From [27] we find that ![]() acts on the domain
acts on the domain 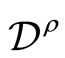 of as follows:
of as follows:


We then define [4] a group action of  on the torus intertwined two-point function
on the torus intertwined two-point function

for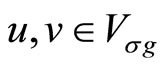 :
:
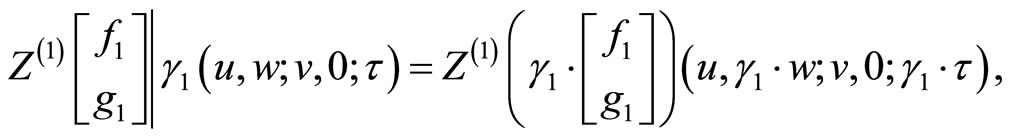
with the standard action 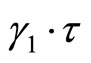 and
and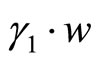 , and
, and
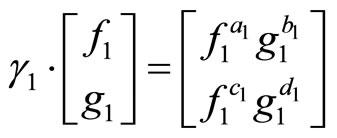 and the torus multiplier
and the torus multiplier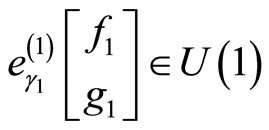 , [1,19]. Then we have [4]
, [1,19]. Then we have [4]
Theorem 24 (Tuite-Z) The torus intertwined twopoint function for the rank two free fermion VOSA is a modular form (up to multiplier) with respect to ![]()
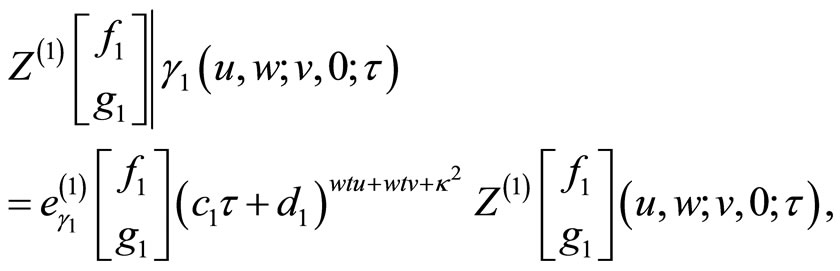
where .
.
The action of the generators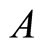 ,
, 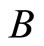 and
and  is given by [1]
is given by [1]
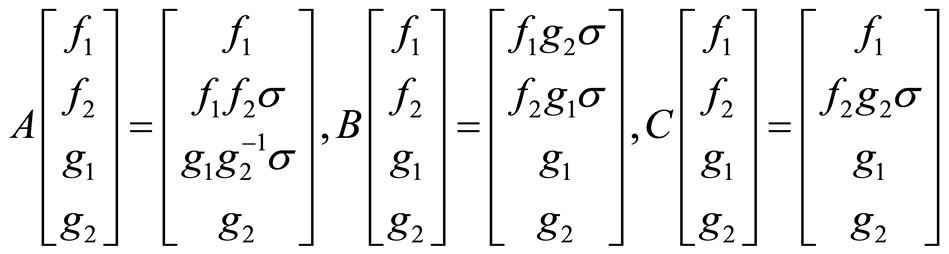 .
.
In a similar way we may introduce the action of 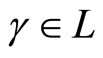 on the genus two partition function [4]
on the genus two partition function [4]


We may now describe the modular invariance of the genus two partition function for the rank two free fermion VOSA under the action of![]() . Define a genus two multiplier
. Define a genus two multiplier 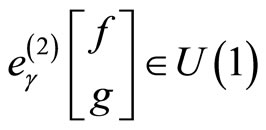 for
for 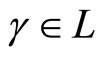 in terms of the genus one multiplier as follows
in terms of the genus one multiplier as follows
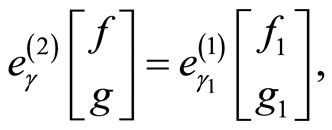
for the generator . We then find [4].
. We then find [4].
Theorem 25 (Tuite-Z) The genus two partition function for the rank two VOSA is modular invariant with respect to ![]() with the multiplier system, i.e.,
with the multiplier system, i.e.,

Finally, we can also obtain modular invariance for the generating form

for all genus two ![]() -point functions [4].
-point functions [4].
Theorem 26 (Tuite-Z) 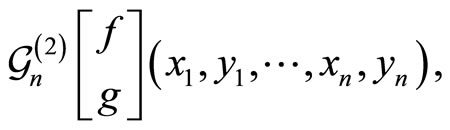
is modular invariant with respect to ![]() with a multiplier.
with a multiplier.
11. Acknowledgements
The author would like to express his deep gratitude to the organizers of the Conference “Algebra, Combinatorics, Dynamics and Applications”, Belfast, UK, August 27-30, 2012.
REFERENCES
- M. P. Tuite and A. Zuevsky, “The Szegö Kernel on a Sewn Riemann Surface,” Communications in Mathematical Physics, Vol. 306, No. 3, 2011, pp. 617-645.
- M. P. Tuite and A. Zuevsky, “Genus Two Partition and Correlation Functions for Fermionic Vertex Operator Superalgebras I,” Communications in Mathematical Physics, Vol. 306, No. 2, 2011, pp. 419-447. http://dx.doi.org/10.1007/s00220-011-1258-1
- M. P. Tuite and A. Zuevsky, “A Generalized Vertex Operator Algebra for Heisenberg Intertwiners,” Journal of Pure and Applied Algebra, Vol. 216, No. 6, 2012, pp. 1253-1492. http://dx.doi.org/10.1016/j.jpaa.2011.10.025
- M. P. Tuite and A. Zuevsky, “Genus Two Partition and Correlation Functions for Fermionic Vertex Operator Superalgebras II,” to Appear, 2013.
- M. P. Tuite and A. Zuevsky, “The Bosonic Vertex Operator Algebra on a Genus g Riemann Surface,” RIMS Kokyuroko, Vol. 1756, No. 9, 2011, pp. 81-93.
- R. E. Borcherds, “Vertex Algebras, Kac-Moody Algebras and the Monster,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 83, No. 10, 1986, pp. 3068-3071. http://dx.doi.org/10.1073/pnas.83.10.3068
- C. Dong and J. Lepowsky, “Generalized Vertex Algebras and Relative Vertex Operators,” Birkhäuser, Boston, 1993. http://dx.doi.org/10.1007/978-1-4612-0353-7
- I. Frenkel, Y. Huang and J. Lepowsky, “On Axiomatic Approaches to Vertex Operator Algebras and Modules,” American Mathematical Society, Providence, Rhode Island, 1993.
- I. Frenkel, J. Lepowsky and A. Meurman, “Vertex Operator Algebras and the Monster,” Academic Press, New York, 1988.
- V. Kac, “Vertex Operator Algebras for Beginners,” University Lecture Series, AMS, Providence, 1998.
- C. Dong, H. Li and G. Mason, “Twisted Representation of Vertex Operator Algebras,” Mathematische Annalen, Vol. 310, No. 3, 1998, pp. 571-600. http://dx.doi.org/10.1007/s002080050161
- C. Dong, H. Li and G. Mason, “Simple Currents and Extensions of Vertex Operator Algebras,” Communications in Mathematical Physics, Vol. 180, No. 3, 1996, pp. 671- 707. http://dx.doi.org/10.1007/BF02099628
- H. Li, “Symmetric Invariant Bilinear Forms on Vertex Operator Algebras,” Journal of Pure and Applied Algebra, Vol. 96, No. 3, 1994, pp. 279-297. http://dx.doi.org/10.1016/0022-4049(94)90104-X
- N. Scheithauer, “Vertex Algebras, Lie Algebras and Superstrings,” Journal of Algebra, Vol. 200, No. 2, 1998, pp. 363-403. http://dx.doi.org/10.1006/jabr.1997.7235
- H. M. Farkas and I. Kra, “Theta Constants, Riemann Surfaces and the Modular Group,” Graduate Studies in Mathematics, AMS, Providence, 2001.
- R. C. Gunning, “Lectures on Riemann Surfaces,” Princeton University Press, Princeton, 1966.
- A. Yamada, “Precise Variational Formulas for Abelian Differentials,” Kodai Mathematical Journal, Vol. 3, No. 1, 1980, pp. 114-143. http://dx.doi.org/10.2996/kmj/1138036124
- D. Mumford, “Tata Lectures on Theta I and II,’’ Birkhäuser, Boston, 1983.
- G. Mason, M. P. Tuite and A. Zuevsky, “Torus N-Point Functions for
 -Graded Vertex Operator Superalgebras and Continuous Fermion Orbifolds,” Communications in Mathematical Physics, Vol. 283, No. 2, 2008, pp. 305- 342. http://dx.doi.org/10.1007/s00220-008-0510-9
-Graded Vertex Operator Superalgebras and Continuous Fermion Orbifolds,” Communications in Mathematical Physics, Vol. 283, No. 2, 2008, pp. 305- 342. http://dx.doi.org/10.1007/s00220-008-0510-9 - C. Dong, H. Li and G. Mason, “Modular-Invariance of Trace Functions in Orbifold Theory and Generalized Moonshine,” Communications in Mathematical Physics, Vol. 214, No. 1, 2000, pp. 1-56. http://dx.doi.org/10.1007/s002200000242
- J. D. Fay, “Theta Functions on Riemann Surfaces,” Lecture Notes in Mathematics, Springer-Verlag, Berlin, 1973.
- J. D. Fay, “Kernel Functions, Analytic Torsion and Moduli Spaces,” American Mathematical Society, Providence, Rhode Island, 1992.
- G. Mason and M. P. Tuite, “On Genus Two Riemann Surfaces Formed from Sewn Tori,” Communications in Mathematical Physics, Vol. 270, No. 3, 2007, pp. 587- 634. http://dx.doi.org/10.1007/s00220-006-0163-5
- Y. Huang, “Two-Dimensional Conformal Geometry and Vertex Operator Algebras,” Birkhäuser, Boston, 1997.
- A. Matsuo and K. Nagatomo, “Axioms for a Vertex Algebra and the Locality of Quantum Fields,” Mathematical Society of Japan, Hongo, Bunkyo-ku, Tokio, 1999.
- G. Mason and M. P. Tuite, “Free Bosonic Vertex Operator Algebras on Genus Two Riemann Surfaces I”, Communications in Mathematical Physics, Vol. 300, No. 3, 2010, pp. 673-713. http://dx.doi.org/10.1007/s00220-010-1126-4
- G. Mason and M. P. Tuite, “Free Bosonic Vertex Operator Algebras on Genus Two Riemann Surfaces II,” arXiv:1111.2264v1.
- G. Mason and M. P. Tuite, “Chiral N-Point Functions for Free Boson and Lattice Vertex Operator Algebras,” Communications in Mathematical Physics, Vol. 235, No. 1, 2003, pp. 47-68. http://dx.doi.org/10.1007/s00220-002-0772-6
- Y. Zhu, “Modular Invariance of Characters of Vertex Operator Algebras,” Journal of the American Mathematical Society, Vol. 9, 1996, pp. 237-302. http://dx.doi.org/10.1090/S0894-0347-96-00182-8
- P. di Vecchia, K. Hornfeck, M. Frau, A. Lerda and S. Sciuto, “N-String, G-Loop Vertex for the Fermionic String,” Physics Letter B, Vol. 211, No. 3, 1988, pp. 301- 307. http://dx.doi.org/10.1016/0370-2693(88)90907-0
- T. Eguchi and H. Ooguri, “Chiral Bosonization on a Riemann Surface,” Physics Letter B, Vol. 187, No. 1-2, 1987, pp. 127-134. http://dx.doi.org/10.1016/0370-2693(87)90084-0
- D. Freidan and S. Shenker, “The Analytic Geometry of Two Dimensional Conformal Field Theory,” Nuclear Physics B, Vol. 281, No. 3-4, 1987, pp. 509-545. http://dx.doi.org/10.1016/0550-3213(87)90418-4
- M. R. Gaberdiel, Ch. A. Keller and R. Volpato, “Genus Two Partition Functions of Chiral Conformal Field Theories,” arXiv:1002.3371, 2010.
- M. R. Gaberdiel and R. Volpato, ‘‘Higher Genus Partition Functions of Meromorphic Conformal Field Theories,” Journal of High Energy Physics, Vol. 9, No. 6, 2009, p. 48.
- N. Kawamoto, Y. Namikawa, A. Tsuchiya and Y. Yamada, “Geometric Realization of Conformal Field Theory on Riemann Surfaces,” Communications in Mathematical Physics, Vol. 116, No. 2, 1988, pp. 247-308.
- F. Pezzella, “g-Loop Vertices for Free Fermions and Bosons,” Physics Letter B, Vol. 220, No. 4, 1989, pp. 544- 550. http://dx.doi.org/10.1016/0370-2693(89)90784-3
- A. K. Raina, “Fay’s Trisecant Identity and Conformal Field Theory,” Communications in Mathematical Physics, Vol. 122, No. 4, 1989, pp. 625-641. http://dx.doi.org/10.1007/BF01256498
- A. Tsuchiya, K. Ueno and Y. Yamada, “Conformal Field Theory on Universal Family of Stable Curves with Gauge Symmetries,” Academic Press, Boston, 1989.
- K. Ueno, “Introduction to Conformal Field Theory with Gauge Symmetries,” Geometry and Physics, Lecture Notes in Pure and Applied Mathematics, Dekker, New York, 1997, pp. 603-745.
- G. Mason and M. P. Tuite, “Vertex Operators and Modular Forms,” In: K. Kirsten and F. Williams, Eds., A Window into Zeta and Modular Physics, Cambridge University Press, Cambridge, 2010, pp. 183-278.

