 Journal of Quantum Informatio n Science, 2011, 1, 7-17 doi:10.4236/jqis.2011.11002 Published Online June 2011 (http://www.SciRP.org/journal/jqis) Copyright © 2011 SciRes. JQIS Application of Scale Relativity (ScR) Theory to the Problem of a Particle in a Finite One-Dimensional Square Well (FODSW) Potential Saeed Naif Turki Al-Rashid1*, Mohammed Abdul-Zahra Habeeb2, Khalid Abdulwahab Ahmed3 1Physics Department, College of Science, Al-Anbar University, Anbar, Iraq 2Physics Department, College of Science, Al-Nahrain University, Baghdad, Iraq 3Physics Department, College of Science, Al-Mustansiriyah University, Baghdad, Iraq E-mail: sntr2006@yahoo.com Received April 16, 2011; revised May 22, 2011; accepted June 1, 2011 Abstract In the present work, and along the lines of Hermann, ScR theory is applied to a finite one-dimensional square well potential problem. The aim is to show that scale relativity theory can reproduce quantum mechanical results without employing the Schrödinger equation. Some mathematical difficulties that arise when obtain- ing the solution to this problem were overcome by utilizing a novel mathematical connection between ScR theory and the well-known Riccati equation. Computer programs were written using the standard MATLAB 7 code to numerically simulate the behavior of the quantum particle in the above potential utilizing the solu- tions of the fractal equations of motion obtained from ScR theory. Several attempts were made to fix some of the parameters in the numerical simulations to obtain the best possible results in a practical computer CPU time within limited local computer facilities. Comparison of the present results with the corresponding re- sults obtained from conventional quantum mechanics by solving the Schrödinger equation, shows very good agreement. This agreement was improved further by optimizing the parameters used in the numerical simu- lations. This represents a new example where scale relativity theory, based on a fractal space-time concept, can accurately reproduce quantum mechanical results without invoking the Schrödinger equation. Keywords: Square Well, ScR Theory, Numerical Simulations, Fractal Space-Time 1. Introduction The extension of the principle of relativity gives new theory of relativity, which is the scale relativity (ScR) theory as introduced by Nottale [1-3] in 1993. This the- ory states that: “the fundamental laws of nature apply whatever the state of scale of the coordinate system”. The state of a reference system is characterized by the resolutions at which this system is observed. It can be defined only in a relative way. The main idea of ScR theory is to give up the arbitrary hypothesis of differen- tiability of space-time. This theory reformulated quantum mechanics from first principles leading to the covariance and geodesic equations by considering a particle as a geodesic in fractal space-time. ScR theory applies in the three domains of microphysics, cosmology and complex systems [2-9]. As far as quantum mechanics is concerned, Nottale and co-workers were able to apply the theory to solve many problems, especially those related to the concep- tual and interpretation aspects. In this connection, we mention the work on the derivation of the postulates of quantum mechanics from the first principles of the ScR theory [10]. In terms of the results of this work, all quantum mechanics and not only the Schrödinger equa- tion, arises as a direct consequence of the fractality of space-time. The extension of the ScR theory to the deri- vation of the main equations of relativistic quantum me- chanics [11] and the relationship between the classical and quantum regimes [12] have been also discussed on the basis of the ScR theory, among other important con- sequences and implications. With all these far reaching aspects of the theory, direct investigations which would shed light on the basic workings of the ScR theory as formulated by Nottale seem to be warranted. In this regard, Hermann [13] was the first, and to our  8 S. N. T. AL-RASHID ET AL. knowledge, the only researcher, who directly applied the fractal equations of motion obtained from ScR theory in terms of a large number of explicit numerically simu- lated trajectories for the case of the quantum-mechanical problem of a free particle in an infinite one-dimensional box [14-17]. He constructed a probability density from these trajectories and recovered in this way the solution of the Schrödinger equation without explicitly using it. The results of this work as originally obtained by Hermann [13] are considered as pioneering in this respect since they show the importance of the direct application of ScR theory to quantum systems to reveal how quantum behavior arises from the fractality of space-time. They also demonstrate the validity of this theory and lay the ground for the numerical methods needed in such appli- cations. It is believed that the results of more applications are important to prove the direct validity of ScR theory in more general cases and not only in a single isolated case as done by Hermann [13]. Besides, such applications are expected to reveal some novel concepts, such as the connection between ScR theory and the Riccati equation [18-21] as revealed in the present work and not observed by Hermann [13] before. 2. Equation of Motion As for a particle in an infinite square well potential, one may start with the complex Newton Equation [10]: ð dt um V (1) where u is a scalar potential and V is a complex velocity, then separate this equation into real and imaginary parts. Also, for this problem the average classical velocity v of the particle is expected to be zero [13]. Then, the equa- tions of motion reduce to the forms: (.) 0 d DUUU u U t (2) where U is the imaginary part of complex velocity and D is the diffusion coefficient. If one takes the 1st of Equa- tions (2) and rewrite it for one-dimension as: 2 11 2 DUxUxu x xx mx (3) then, integrating, one obtains: 2 1 11 2 DUx Uxcux xm (4) where c1 is a constant of integration. According to Hermann’s Scale-Relativity method [13], c1=E/m. Then, Equation (4) can be written in the form: 2 d2 d m UxU xuxE x (5) where 2 Dm . Equation (5) has the form of a Riccati Equation [18,19]. To solve this equation, one may trans- form it into a 2nd order differential equation [18,19] of the form, 20ryxr qxyx (6) where [18,19], 1yx Ux ryx (7) and x is an arbitrary function of x. From equation (5), it follows that: m r ; 2 qxux E (8) Using Equation (8), Equation (6) becomes, 2 22 d2 0 d m yxux Eyx x x (9) Depending on the values of E, there are two general classes for the solution of Equation (9) [14,22,23] which are: Bound state solution if 0 Eu; the particle is con- fined to the region of potential well. Free particle state solution if 0 Eu; the particle is free to reach x = ± . In the present problem, the case 0 is assumed. There are three regions of potential in the problem of a finite square well that are [14,22]: Eu 0 0 uata uxatax a uatx a 0 (10) Then, the general solutions of Equation (9) are given by [14-17,23]: 1 2 3 cos sin Kx Kx Kx Kx yxGeGefor xa yxAxBx foraxa yxHeHefora x (11) where G, G , A, B, H and H are arbitrary constants, κ2 2/mE and 2 0 2KmuE/. Applying the boundary conditions at x ± , this leads to x 0. Then, one can rewrite Equations (11) as: Copyright © 2011 SciRes. JQIS  S. N. T. AL-RASHID ET AL. 9 1 2 3 cos sin Kx Kx yx Ge yx AxBx yx He (12) The next step is to apply the matching conditions at the boundaries between regions, which require that both function and its derivative be continuous. In this way, one gets a set of four homogeneous linear equations with four unknowns [19]: (1) cos sin sin cos Kx Ka GeAa Ba or xa KGeAa Ba (13) (2) cos sin sin cos Ka Ka AaBaHe or xa AaB aKHe (14) These equations can be rewritten in matrix form as: cos sin0 sin cos00 cossin 0 coscos 0 Ka Ka Ka Ka aae AA aaKeBB GG aa e HH aaKe M (15) where the matrix M is given by: cos sin0 sin cos0 cossin 0 cos cos0 Ka Ka a a aae aaKe aa e aaKe M (16) The trivial solution of Equation (15) is A = 0, B = 0, G = 0 and H = 0 [23]. While, for a non-trivial solution to exist, the condition [23]: detM = 0 (17) must be satisfied. To simplify, one eliminates the coeffi- cients G and H. Then, Equation (15) becomes the 2 × 2 matrix equation [23]: 0 tantan tantan B A M B A aKKa aKKa (18) For this equation to have a non-trivial solution, the de- terminant of the coefficients must be equal to zero, or: 2tantan 0aK Ka (19) Then, there are two solutions which are [23]: (a) κ tan κ=K, this means B =0 and a 2cos xA x (20) (b) K tan κ= κ, this means A = 0 and a 2sin xB x (21) Equation (20) corresponds to even parity solutions while Equation (21) corresponds to odd parity solutions. These equations can be simplified by introducing the new dimensionless variables: a and = K (22) a From the definition of κ and K, one can write: 22 0 2 2m u (23) Using Equation (22), one can rewrite Equations (20), (21) and (23) in the forms: = tan (24) = – cot (25) 22 2 2 2m xua 2 (26) where the dimensionless parameter measures the vol- ume of the potential in unit of ħ2/2 m. 2 0 ua To determine the values of κ and K in Equations (24) and (25), one may solve these equations graphically together with Equation (26) [14-17,22,23]. Figures (1) and (2) give the intercepts for the even parity solution (Equation (24)) and the odd parity solution (Equation (25)) for two sets of values of the potential volume parameter ( = 1 and 4) and ( = 2 and 6) for the even and odd parity solutions respectively. In these figures, κ is drawn horizontally and vertically. The dashed curve is that of tan (for even parity) or cot (for odd parity). The continuous curve is that of 22 x2 The values of κ and K (x and ) corresponding to the solutions of Equations (24), (25) and (26) can be deter- mined from Figures (1) and (2). Then, one can calculate the state energy and the function for different val- ues of in the following way: )(xy (1) For =1 (equivalent to n = 1), x 0.7391 and = 0.673. This is called the ground state energy, which is: 22 2 2 0.7391 0.273 2 gs Ema ma 2 (27) Copyright © 2011 SciRes. JQIS 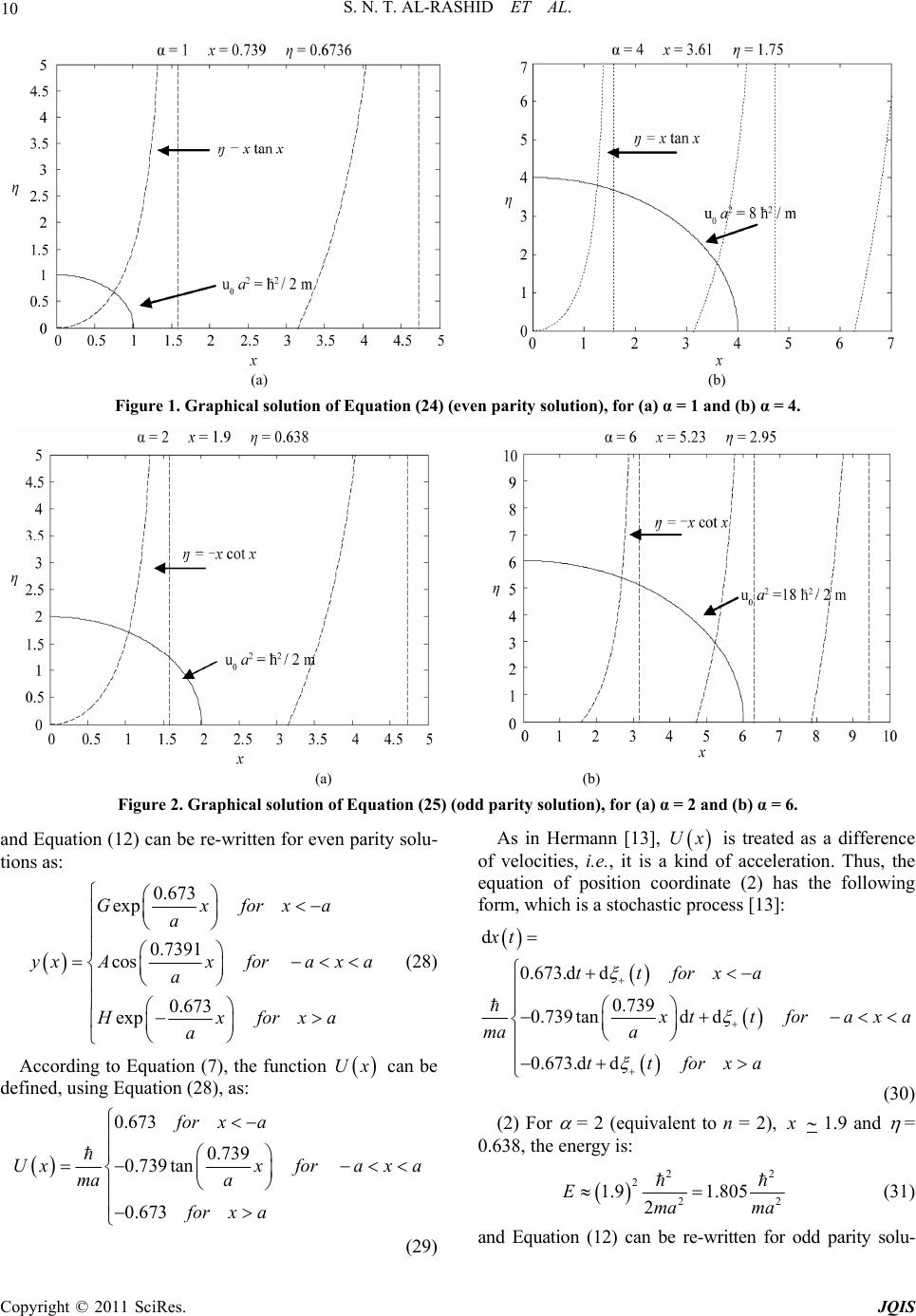 S. N. T. AL-RASHID ET AL. Copyright © 2011 SciRes. JQIS 10 (a) (b) Figure 1. Graphical solution of Equation (24) (even parity solution), for (a) α = 1 and (b) α = 4. (a) (b) Figure 2. Graphical solution of Equation (25) (odd parity solution), for (a) α = 2 and (b) α = 6. and Equation (12) can be re-written for even parity solu- tions as: 0.673 exp 0.7391 cos 0.673 exp Gxforxa a yxAxforaxa a Hxforx a As in Hermann [13], Ux is treated as a difference of velocities, i.e., it is a kind of acceleration. Thus, the equation of position coordinate (2) has the following form, which is a stochastic process [13]: a (28) d 0.673.dd 0.739 0.739 tandd 0.673.dd xt ttforxa ttforax ma a ttforxa a (30) According to Equation (7), the function can be defined, using Equation (28), as: Ux 0.673 0.739 0.739tan 0.673 for xa Uxxforax a ma a for xa (2) For = 2 (equivalent to n = 2), 1.9 and = 0.638, the energy is: 22 2 2 1.9 1.805 2 Ema ma 2 (31) and Equation (12) can be re-written for odd parity solu- (29)  S. N. T. AL-RASHID ET AL. 11 tions as: 0.638 exp 1.9 sin 0.638 exp Gxforx a yxBxforaxa a a xforxa a (32) Also, 0.638 1.9 1.9cot 0.638 for xa Uxxforaxa ma a for xa (33) and, d 0.638.dd 1.9 1.9cotd d 0.638.d d xt ttforxa ttforax ma a ttforxa a (34) (3) For = 4 (equivalent to n = 3), x = 3.61 and = 1.75, the energy is: 2 2 6.51Ema (35) and Equation (12) for even parity solutions becomes: 1.75 exp 3.61 cos 1.75 exp Gxforxa a yxAxforax a a Hxforx a a (36) Again, 1.75 3.61 3.61tan 1.75 for xa Uxxforax a ma a for xa (37) and, d 1.75d d 3.61 3.61tand d 1.75d d xt ttforxa ttforax ma a ttforxa a (38) (4) For = 6 (equivalent to n = 4), x = 5.23 and = 2.95, the energy is: 2 2 13.6Ema (39) and Equation (12) for odd parity solutions becomes: 2.95 exp 5.23 sin 2.95 exp Gxforxa a yxBxforax a a Hxforx a a (40) Also, 2.95 5.23 5.23cot 2.95 for xa Uxxforax a ma a for xa (41) and, d 2.95d d 5.23 5.23cotd d 2.95dd( ) xt ttforxa ttforax ma a ttforxa a (42) where d +(t) is a random variable of a Gaussian distribu- tion with width 2dDt [13]. 3. Numerical Simulations To simplify Equations (30), (34), (38) and (42), one can take 2Ddt = 1 [13], then, these equations become: (1) = 1 Copyright © 2011 SciRes. JQIS  12 S. N. T. AL-RASHID ET AL. d 0.673 0,1 10.739 0.739tan0,1 0.6730,1 xt Nforxa Nforax aa Nforxa a (43) (2) = 2 d t 0.638 0,1 11.9 1.9cot 0, 1 0.6380,1 Nforxa Nforax aa Nforxa a (44) (3) = 4 d 1.75 0,1 13.61 3.61tan 0,1 1.75 0,1 xt Nforxa Nforax aa Nforxa a (45) (4) = 6 d 2.95 0,1 15.23 5.23cot 0,1 2.95 0,1 xt Nforxa Nforax aa Nforxa a (46) where N (0, 1) is a normalized random variable [10]. A computer program was written (see Appendix A), following Hermann’s procedure [13], to make numerical simulations for the FODSW problem. Numerical simula- tions are performed using Equations (43), (44), (45) and (46) which represent trajectory equations of the particle for different value of . The output of these simulations gives the probability density ƒ(x) of the particle in a fi- nite square well potential. To construct it, one may di- vide the region into 1800 pieces (boxes), which gives the best results. This choice comes after many numerical tests. Here, one chooses the time step equal to 5 108 which gives best results also after many numerical tests. The x position in the region will be drawn horizontally and the number of occurrences vertically. So, a point of the curves to be drawn has to be understood as (x, y); x is the number of boxes and y is the number of time steps for which the particle was in box x. The continuous curves indicate the results of the present simulations and the dashed curves the results of conventional quantum mechanics, with the same normalization as the numerical results. The results are always normalized by multiplying the number of occurrences in each box by the total num- ber of boxes which is a. The probability density P(x) of conventional quantum mechanics, which will be compared with the present re- sults, is given by: (1) For even parity solutions: 2 1 22 2 2 3 exp 2 cos exp 2 Px x Nforx a x Nxforax a x Nforx a a a a (2) For odd parity solutions: 2 4 22 5 2 6 exp 2 sin exp 2 Px x Nforx a x Nxforax a x Nforx a a a a 6 where are normalization constants [14-18]. 1 ,...,NN For = 1, 2, 4 and 6 this probability density is given by [23]: (1) = 1 2 0.844exp 1.3 10.4019cos 0.739 0.844exp 1.3 xfor xa a x Pxfora x a aa xfor x a a (47) (2) = 2 2 1.4304exp 1.27 10.445sin 1.9 1.4304exp 1.27 x or xa a x Pxforax a aa x or xa a (48) Copyright © 2011 SciRes. JQIS 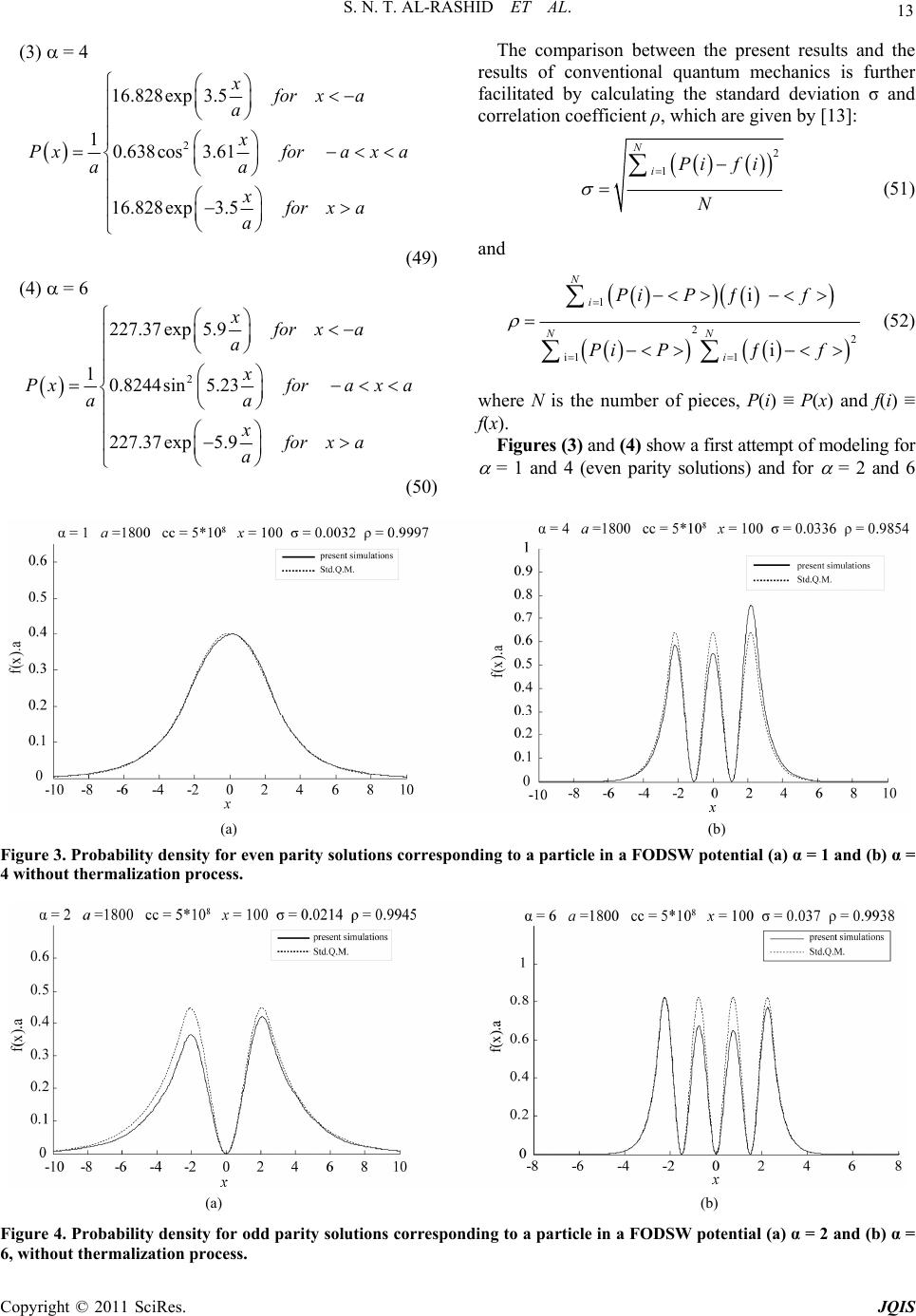 S. N. T. AL-RASHID ET AL. Copyright © 2011 SciRes. JQIS 13 (3) = 4 2 16.828exp 3.5 10.638cos 3.61 16.828exp 3.5 xfor xa a x Pxforax a aa xfor xa a The comparison between the present results and the results of conventional quantum mechanics is further facilitated by calculating the standard deviation σ and correlation coefficient ρ, which are given by [13]: 2 1 N iPif i N (51) and (49) (4) = 6 2 227.37exp5.9 10.8244sin 5.23 227.37exp5.9 xfor xa a x Pxforax a aa xfor xa a 1 22 i1 1 ƒi ƒi N i NN i Pi Pf Pi Pf (52) where N is the number of pieces, P(i) ≡ P(x) and f(i) ≡ f(x). Figures (3) and (4) show a first attempt of modeling for = 1 and 4 (even parity solutions) and for = 2 and 6 (50) (a) (b) Figure 3. Probability density for even parity solutions corresponding to a particle in a FODSW potential (a) α = 1 and (b) α = 4 without thermalization process. (a) (b) Figure 4. Probability density for odd parity solutions corresponding to a particle in a FODSW potential (a) α = 2 and (b) α = 6, without thermalization process.  14 S. N. T. AL-RASHID ET AL. Figure 5. Probability density for α = 6 (odd parity solution corresponding to a particle in a FODSW potential after y. The numerical simula- present work that the behavior of a Prof. Dr. L. Nottale (Di- Paris, France) for clarifying theory of scale relativity and The Theory of Scale Relativity,” Interna- of Modern Physics A, Vol. 7, No. 20, -4936. doi:10.1142/S0217751X92002222 ) increasing the number of boxes. (odd parity solutions) respectivel tions start with arbitrary point which is x = 100 (corre- sponding to box No. 100). In these figures, there is a clear difference between the present results and the results of quantum mechanics, that is measured by and ρ. Hermann [13] indicated in his work that the simula- tions were restarted after 105 steps, or more, with a new starting position. Then, better thermalization of the sys- tem is obtained and convergence is increased. Tests in the present work indicated that the thermalization proc- ess as used by Hermann [13] cannot be applied here without fixing additional parameters. This required very long computer time and, therefore, was not adopted in the present work. However, these tests also indicated that the present results can be improved by increasing the number of divisions of a (i.e., number of boxes). Figure (5) shows the results obtained for = 6 after increasing the number of boxes from 1800 to 2200. 4. Conclusions It can be seen from the quantum particle in an infinite one-dimensional square well potential can be obtained without explicitly writing the Schrödinger equation or using any conventional quantum axiom. This leads one to conclude from the present work that ScR is a well-founded theory for deriving quantum mechanics from the concept of fractal space-time. Even though many of the aspects of Hermann’s work were used in the present work as they are, the application of his approach to the present quantum mechanical prob- lem was not a direct one. Successful applications were not achievable without, among other things, a new ad- justment for the time step dt after some deeper under- standing of the underlying particle motion in the present problem. It is expected that this understanding is neces- mechanical problems along the lines of Hermann’s work [13] and the present work. It is also concluded from the attempts made in the present work to improve the results of numerical simulation by parameter optimization, that such attempts are successful in achieving some im- provement, and that further improvement is possible, but requires more computer time. 5. Acknowledgments e would like to deeply thank sary when attempts are made to solve other quantum W rector of Research, CNRS, ome points regarding his s for supplying some literature and Dr. R. Hermann (Dept. of Physics, Univ. de Liege, Belgium) for his sug- gestions concerning further applications of the theory of scale relativity. 6. References ] L. Nottale, “[1 tional Journal 1992, pp. 4899 ] L. Nottale, “Fractal Space-Time and Microphy[2 sics: To- wards a Theory of Scale Relativity,” World Scientific, Singapore, 1998. [3] L. Nottale, “The Scale Relativity Program,” Chaos, Soli- tons and Fractals, Vol. 10, No. 2-3, 1994, pp. 459-468. doi:10.1016/S0960-0779(98)00195-7 [4] L. Nottale, “Scal App e Relativity and Fractal Space-Time: , 779(96)00002-1 lication to Quantum Physics, Cosmology and Chaotic Systems,” Chaos, Solitons and Fractals, Vol. 7, No. 6 1996, pp. 877-938. doi:10.1016/0960-0 [5] L. Nottale, “Scale Relativity, Fractal Space-Time and Quantum Mechanics,” Chaos, Solitons and Fractals, Vol. 4, No. 3, 1994, pp. 361-388. doi:10.1016/0960-0779(94)90051-5 [6] L. Nottale, “Scale Relativity, Fractal Space-Time and Morphogenesis of Structures”, Sciences of the Interface, Proceedings of International Symposium in Honor of O. Rossler, ZKM Karlsruhe, 2000, p. 38. [7] L. Nottale, “Scale Relativity,” Reprinted from “Scale In- variance and Beyond,” In: B. Dubralle, F. Graner and D. Sornette, Eds., Proceedings of Les Houches, EDP Sci- ence, 1997, pp. 249-261. [8] L. Nottale, “Scale Relativity and Quantization of the Uni- verse-I, Theoretical Framework,” Astronomy and Astro- physics, Vol. 327, No. 3, 1997, pp. 867-889. [9] L. Nottale, G. Schumacher and J. Gray, “Scale Relativity and Quantization of the Solar System,” Astronomy and Astrophysics, Vol. 322, No. 3, 1997, pp. 1018-1025. [10] L. Nottale and M. N. Célérier, “Derivation of the Postulates of Quantum Mechanics from the First Principles of Scale Copyright © 2011 SciRes. JQIS  S. N. T. AL-RASHID ET AL. 15 Relativity,” Journal of Physics A: Mathematical and Theoretical, 2007, Vol. 40, No. 48, pp. 14471-14498. doi:10.1088/1751-8113/40/48/012 [11] M.-N. Célérier and L. Nottale, “Electromagnetic Klein- Gordon and Dirac equations in scale relativity,” Interna- tional Journal of Modern Physics A, Vol. 25, No. 22, 2010, pp. 4239-4253. [12] om the Classical to the L. Nottale, “On the Transition fr Quantum Regime in Fractal Space-Time Theory,” Chaos, Solitons and Fractals, 2005, Vol. 25, No. 4, pp. 797-803. doi:10.1016/j.chaos.2004.11.071 [13] R. P. Hermann, “Numerical Simulation of a Quantum Particle in a Box,” Journal of Physics A: Mathematical and General, Vol. 30, No. 11, 1997, pp. 3967-3975. doi:10.1088/0305-4470/30/11/023 [14] cs,” 3rd Edition, Int. [16] Quantum Mechanics oё, “Quantum me- [18] cademic [19] fferen- L. I. Schiff., “Quantum Mechani Stu- dent, McGraw-Hill, New York, 1969. [15] S. Gasiorowicz, “Quantum Physics,” John Wiley and Sons, New York, 1974. Addi J. L. Powell and B. Crasemann, “,” son-Wesley Co., Inc., Massachusetts, 1961. [17] C. C. Tannoudji, B. Diue and F. Lal chanics,” John Wiley and Sons, New York, 1977. W. T. Reid, “Riccati Differential Equations,” A Press, New York, 1972. F. Charlton, “Integrating Factor for First-Order Di tial Equations,” Classroom Notes, Aston University, Bir- mingham, 1998. [20] N. Bessis and G. Bessis, “Open Perturbation and Riccati Equation: Algebraic Determination of Quartic Anhar- monic Oscillator Energies and Eigenfunctions,” Journal of Mathematical Physics, Vol. 38, No. 11, 1997, pp. 5483-5492. doi:10.1063/1.532147 [21] G. W. Rogers, “Riccati Equation and Perturbation Expan- sion in Quantum Mechanics,” Journal of Mathematical Physics, Vol. 26, No. 14, 1985, pp. 567-575. doi:10.1063/1.526592 [22] R. H. Dicke and J. P. Wittke, “Introduction to Quantum Mechanics,” Addison-Wesley Co., Inc., Massachusetts, 1960. [23] D. Počanić, “Bound State in a One-dimensional Square Potential Well in Quantum Mechanics,” Classroom Notes, University of Virginia, Charlottesville, 2002. Copyright © 2011 SciRes. JQIS 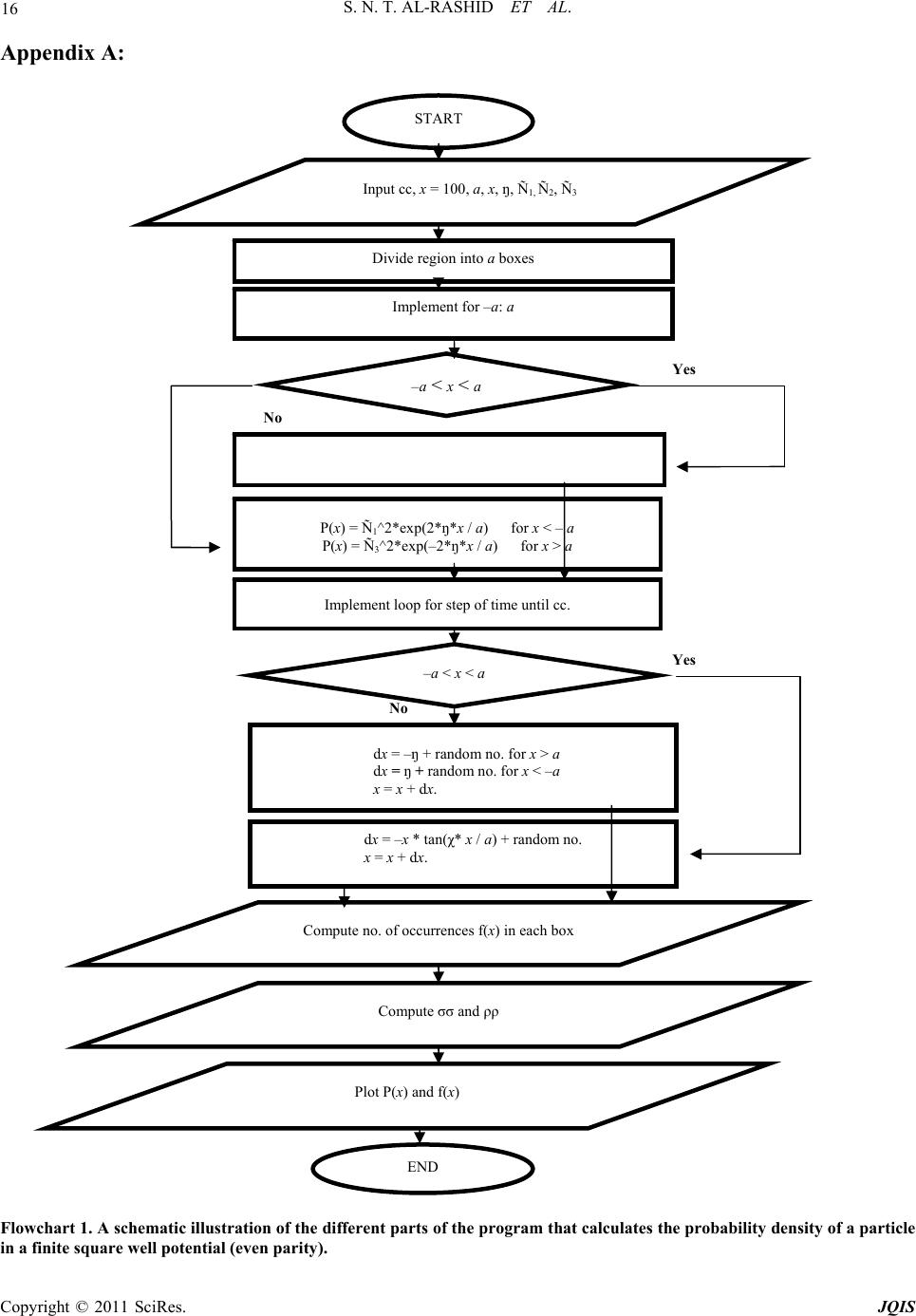 S. N. T. AL-RASHID ET AL. 16 ppendix A: lowchart 1. A schematic illustration of the different parts of the program that calculates the probability density of a particle square well potential (even parity). A F in a finite Implement for –a: a START Input cc, x = 100, a, x, ŋ, Ñ1, Ñ2, Ñ3 Divide region into a boxes –a < x < a P(x) = Ñ1^2*exp(2*ŋ*x / a) for x < – a P(x) = Ñ3^2*exp(–2*ŋ*x / a) for x > a Implement loop for step of time until cc. –a < x < a dx + random no. for x > a dx = ŋ + random no. for x < –a = –ŋ x = x + dx. dχ* x / a) + random no. x = x + dx. x = –x * tan( Compute no. of occurrences f(x) in each box Compute σσ and ρρ Yes Yes No No Plot P(x)andf(x) END Copyright © 2011 SciRes. JQIS 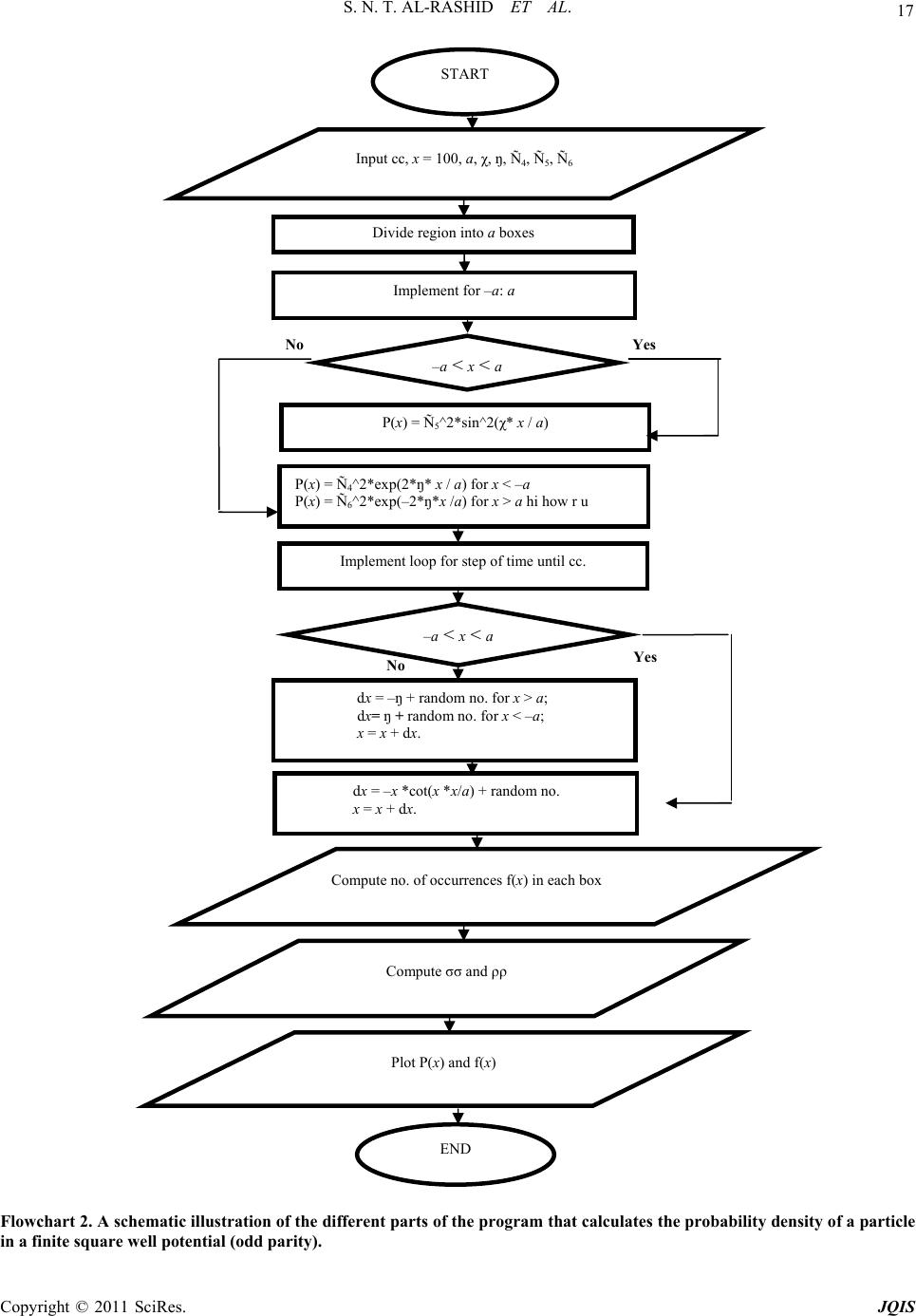 S. N. T. AL-RASHID ET AL. Copyright © 2011 SciRes. JQIS 17 Flowchart 2. A schematic illustration of the different parts ofrogram that calculates the probability density of a particle a finite square well potential (odd parity). Input cc, x = 100, a, χ, ŋ, Ñ4, Ñ5, Ñ6 Divide region into aboxes Yes Yes No No Implement for –a: a START a< < a P(x) = Ñ* x / a) 5^2*sin^2(χ P(x) = Ñ4^2*e P(x) = Ñ6^2*exp(–2*ŋ*x /a) for x > a hi how r u xp(2*ŋ* x / a) for x < –a Implement loop for step of time until cc. –a< x< a dx = –ŋ + rr x > a; dx= ndom no. for x < –a; x = x. andom no. fo ŋ + ra + dx dx = –x *cot(x *x/a) + random no. x = x + dx. Comrences f(x) in each boxpute no. of occur Compute σσ and ρρ Plot P(x) and f(x) END the p in
|