Journal of Global Positioning Systems (2005)
Vol. 4, No. 1-2: 192-200
Comparative study of interpolation techniques for ultra-tight
integration of GPS/INS/PL sensors
S.Ravindra Babu and Jinling Wang
School of Surveying and Spatial Information Sy s tem s, University of New South Wales, Sydney - 2052, Austral ia
Received: 26 November 2004 / Accepted: 12 July 2005
Abstract: Ultra-tight architecture plays a key role in
improving the robustness of the integrated GPS/INS/PL
(Pseudolite) system by aiding GPS receiver’s carrier
tracking loops with the Do ppler information d erived from
INS (Inertial Navigation System) velocity measurements.
This results in a lower carrier tracking loop bandwidth
and subsequent improvement in measurement accuracy.
Some other benefits using this architecture include:
robust cycle-slip detection and correction, improved anti-
jam performance, and weak signal detection.
Typically the integration/navigation filter run at a rate of
1 to 100 Hz, which is insufficient to aid the carrier
tracking loop as such loops normally run at about 1000
Hz. Two approaches were envisioned to solve this
problem. One approach is to run the navigation Kalman
filter at a higher rate, and the other is to run the filter at a
lower rate and interpolate the measurements to the
required rate. Although the first approach seems to be
straightforward, it is computationally very intensive and
requires a huge amount of processing power, adding to
the cost and complexity of the system. The second
method interpolates the low rate Doppler measurements
from the navigation filter using multirate signal
processing algorithms. Due to its efficiency and simpler
architectures the interpolation method is adopted here.
Filtering is the key issue when designing interpolators as
they remove the images caused in the upsampling
process. Although direct form of filtering can be
adopted, they increase the computations. To reduce the
computational burden, two efficient ways of
implementing the interpolators are proposed in this paper:
Polyphase and CIC (Cascaded Integrator Comb). The
paper summarizes the design and analysis of these two
techniques, and our initial results suggest that CIC is
relatively better in terms of performance and
computational requirements.
Keywords: Tracking loops, Doppler, INS, interpolators,
Polyphase, CIC.
1 Introduction
A conventional GPS receiver can track the signal if the
received power and the vehicle dynamics are within its
operational limits. But, the demands of the proliferating
applications are much more. The receiver is expected to
operate in reduced signal strength, multipath,
interference, intentional and unintentional jamming
environments. Moreover, automotive applications
involve dynamics such as acceleration and jerk.
Unfortunately, optimizing a single receiver to meet all
these requirements is almost an impossible task; the
design is usually optimized to cater to a particular
environment. However, adding additional sensors not
only increases its operational areas but also its reliability
and robustness, and in fact it is this philosophy th at drives
the growth of integrated GPS/INS systems. Of many
possible sensors, inertial navigation system (INS) is
found to be optimal due to its immunity to
electromagnetic signals and also its ability to provide
navigation data at highe r dat a rat es.
Increasingly, Pseudolites (ground based GPS
transmitters) are also seen as attractive aiding sensors
primarily due to their capability to improve the
geometrical strength, and also providing signals at places
where GPS signals cannot be received (Wang et al.,
2001). In the loose, tight and ultra-tight integration
architectures, the time dependent systematic errors of the
inertial sensor are calibrated using precise
GPS/Pseudolite positioning solutions. During loss of
GPS signals, Pseudolites can continue to calibrate the
inertial sensor errors thereby improv ing the robustness of

Babu et al.: Comparative Study of Interpolation Techniques for ultra-tight integration of GPS/INS/PL 193
the integrated architecture. Therefore, for applications
such as indoors, foliage etc., integrating Pseudolites with
GPS and INS systems will certainly improve the
performance especially in terms of robustness and
reliability.
The integrated GPS/INS/Pseudolite systems are not new
in the field of navigation, and are being developed for
nearly two decades; however, the architectures in which
these two systems can be integrated have changed over
the period of time. The principal idea behind these
architectures is if GPS or a Pseudolite can calibrate
inertial sensor errors during normal operation, then the
calibrated INS can provide navigation during GPS
outages. Traditionally, both these systems were integrated
in the so called loosely coupled architecture, where the
navigation solutions from both the systems were
combined in an external Kalman filter to provide an
optimal solution. Though the implementation of this
system looks simple, nevertheless there are limitations in
this type of architecture (Farrell, 2000). To overcome
some of these shortcomings, tightly coupled architecture
was developed where a GPS/Pseudolite receiver is not
considered as a navigation system but as a sensor that
provides pseudo-ranges (PR) and pseudo range-rates
(PRR) which can be integ rated with INS variables. Some
of the advantages of this system are: it can provide
navigation even with one satellite though with a
degradation, and lesser correlation of the integration
variables (PR, PRR) reduces the complexity of the
integration Kalman filter.
The recent development in this series is the Ultra-tight
integration, i.e. integration of I (in-phase) and Q
(quadrature) variables from the receiver’s tracking loops
with INS. The inherent property of this system is the
integration of INS derived Doppler feedback to the
carrier tracking loops. This forms an important
advantage of this system, as the INS Doppler aiding
removes the vehicle Doppler from the GPS/Pseudolite
signal, it facilitates a significant reduction in the carrier
tracking loop bandwidth (Babu & Wang, 2004); on a
comparative scale the dynamics on the pseudorandom
noise code is very less due to its low frequency nature.
The bandwidth reduction improves the anti-jamming
performance of the receiver, and also increases the post
correlated signal strength. In addition, due to lower
bandwidths, the accuracy of the raw measurements is also
increased.
But, the INS aiding of th e receiver tracking loops require
higher Doppler update rates from INS. As the update rate
of the tracking loops is normally about 1 KHz, the
derived Doppler rates should be generated at the same
rate for the aiding to be efficient. One possible method is
to run the Kalman filter at a high rate, i.e. 1000 Hz;
however, this requires an extensive processing power.
The second method is to generate Doppler at lower rates
and then interpolate to the required rate (Beser et al.,
2000; Gardner, 1993). This is the method adopted in this
paper. The Kalman filter from which the Doppler is
generated typically runs at 1 or 100 Hz, and the Doppler
measurement is then interpolated by a factor of 10 or 100
for aiding.
An increase in sampling rate can be accomplished by
using interpolators which can efficiently be designed
using multi-rate signal processing techniques (Mitra,
1999; Crochiere & Rabiner, 1983). A lowpass FIR (finite
impulse response) filter is used in the interpolators to
remove the images caused in the upsampling process.
The filter transfer function is efficiently realized using
Polyphase and CIC (Cascaded integrator comb)
techniques (Hentschel, T., & Fettweis, 1990). While the
polyphase method involves decomposing the filter
transfer function into parallel stages, CIC implements the
interpolator transfer function without using multipliers.
This paper discusses on the design issues of both these
techniques with their advantages and disadvantages.
2 Doppler estimates from INS
The GPS/Pseudolite receiver computes its velocity by
measuring the Doppler offsets on the GPS and Pseudolite
signals. Therefore, measuring the Doppler signal
accurately becomes imperative. After down converting
the L1 signals to IF (intermediate frequency), the
acquisition loops co arsely measures the carrier frequ ency
and code offsets, and then pass these coarse
measurements to the tracking loops for fine tracking.
Due to their low loop bandwidths (typically about 12 to
18 Hz), the tracking loops are sensitive to the Doppler
changes, whereas acquisition loops with a Doppler bin
size of about 500 Hz are almost insensitive except in
circumstances of very high dynamics. This places severe
constraints on the tracking loops. For tracking high
dynamics (acceleration and jerk), the bandwidth should
be greater than 18 Hz with the order of the loop increased
to 3Hz (Kaplan, 1996); however, this affects the quality
of measurements and stability of the loop.
The received Doppler from satellites and Pseudolites are
given as
_(1 )
rel
rx gpstxva
ffc =−
G
(1)
where tx fis the transmitted GPS/Pseudolite L1
frequency (1575.42 MHz), rtrel vvv −= is the relative
velocity between satellite and receiver, a
G
is the line of
sight vector, and cis the velocity of light. The total
Doppler on the received signal is due to the satellite and
receiver motion, and satellite and receiver clock biases as
shown in equation (2).

194 Journal of Global Positioning Systems
__ _ _
_
rx gpsrx motionsat motionclk bias
sat clk
ff ff
fbias
=+ +
++ (2)
The average rate of change of Doppler due to satellite
motion is about 0.5Hz/s (Tsui, 2000), and the satellite
clock bias is transmitted in the navigation data.
Therefore, ignoring these two terms equation (2) can be
simplified as
biasclkmotionrxgpsrx fff ___ += (3)
The tracking loop bandwidth is determined by the
receiver motion and clock bias as shown in equation (3).
However, with oscillators better than 1 ppm, the Doppler
is primarily dictated by the motion, i.e.
motionrxgpsrx ff __=. The order and bandwidth of the
carrier tracking loop is dete rmined based on the expected
dynamics. If there is only velocity in the receiver motion,
a stable second order tracking loop can be used, but if the
receiver experiences acceleration and jerk, to minimize
the dynamic stress error a 3rd order loop is used. The
design of a 3rd order loop is quite complex and also
causes stability issues (Ward, 1998).
Ultra-tight tracking loop, as shown in Figure 1,
overcomes this by integrating the INS derived Doppler
with the tracking loops. This derived Doppler closely
reflects the Doppler on the GPS and Pseudolite signals
caused due to receiver motion, and if integrated, removes
the Doppler from the base band signal; i.e. the Doppler
due to receiver clock oscillator and any residual bias from
the Kalman filter will only remain. This resid ual Dop pler
is usually small, and therefore, the tracking loop
bandwidth can be reduced to about 3 to 5 Hz.
The Doppler derived from INS is given as
biasresmotionrxinsrxfff ___ += (4)
where biasres
f_is the Doppler caused by the residual
bias in the complementary Kalman filter. Integratin g this
Doppler signal with the tracking loops gives
biasresbiasclk
insrxgpsrxdoppres
ff
fff
__
___
−=
−
=
(5)
Therefore, in the ultra-tightly integrated system, the
bandwidth is determined by the receiver clock bias and
any residual bias in the Kalman filter facilitating a
reduction in the carrier tracking bandwidth. However, to
leverage the benefits from this system the Doppler from
INS should have the same update rate as that requ ired by
the tracking loops. Normally, the update rate of the
integration Kalman filter is about 1 to 100 Hz, but the
tracking loops are updated at about 1 KHz rate.
Interpolators are therefore used to increase the sampling
frequency of Doppler. The subsequent sections discuss
the design and efficient realization of the interpolators.
2.1 Interpolators design for Doppler re-sampling
To convert the low frequen cy INS derived Doppler to the
high frequency rate required by the tracking loops, an
interpolator is required. The design of the interpolator is
critical as any signal distortion will have a direct impact
on the loop bandwidth. In general, the interpolator has
two blocks as shown in Figure 2: an upsampler which
inserts 1
−
L zero samples between two successive input
samples whereL is the interpolation factor, and a low-
pass filter to remove the images caused in the upsampling
process.
Fig. 1 Ultra-tight architecture
11,QI
22
,QI
nn
QI,
][nx
u
][nx ][ny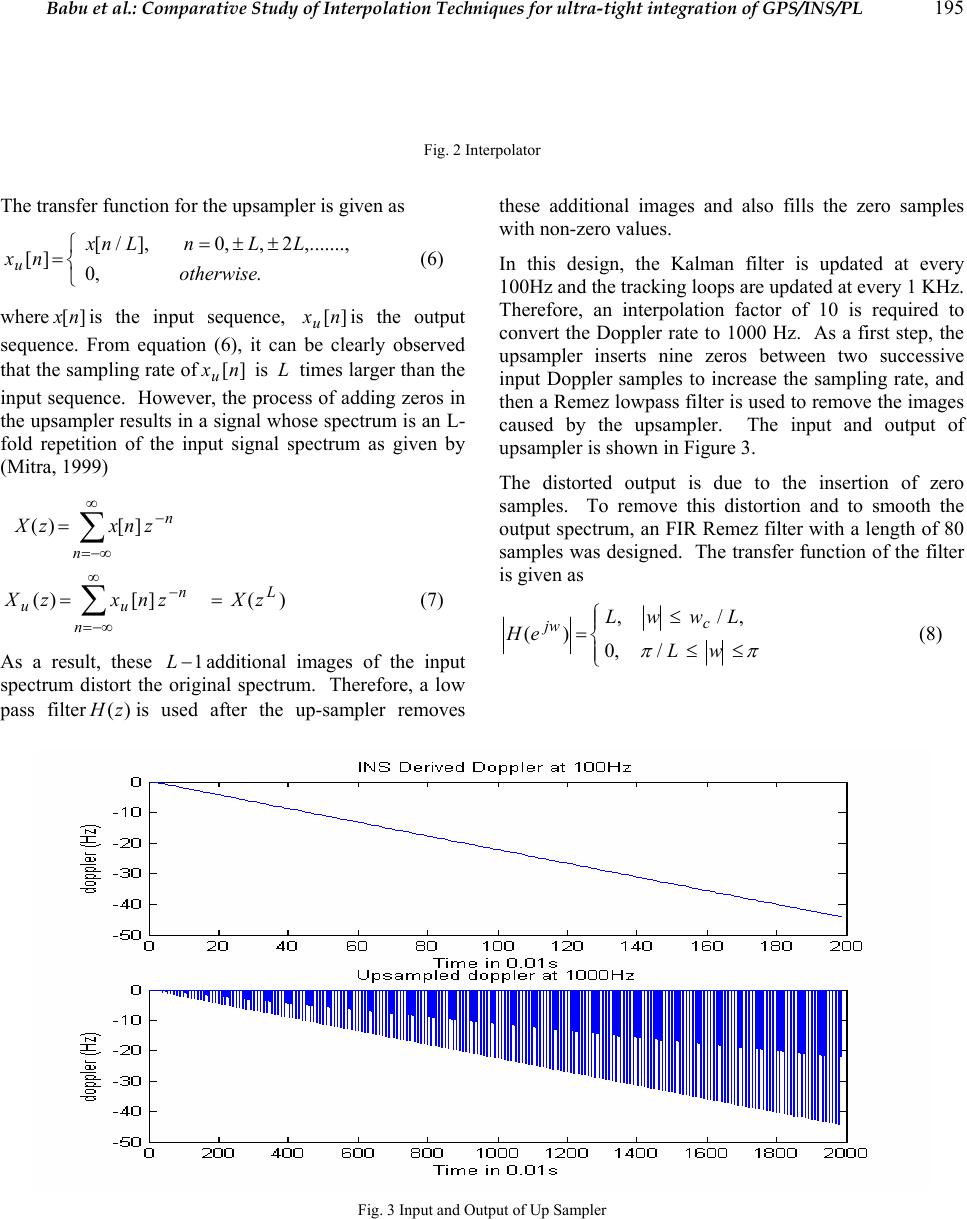

Babu et al.: Comparative Study of Interpolation Techniques for ultra-tight integration of GPS/INS/PL 195
Fig. 2 Interpolator
The transfer function fo r the upsampler is given as
⎩
⎨
⎧±±=
=.,0
,.......,2,,0],/[
][ otherwise
LLnLnx
nxu (6)
where ][nx is the input sequence, ][nxuis the output
sequence. From equation (6), it can be clearly observed
that the sampling rate of][nxu is L times larger than the
input sequence. Ho wever, the process of adding zeros in
the upsampler results in a signal whose spectrum is an L-
fold repetition of the input signal spectrum as given by
(Mitra, 199 9)
n
n
znxzX −
∞
−∞=
∑
=][)(
)(][)( L
n
n
uu zXznxzX== ∑
∞
−∞=
− (7)
As a result, these 1−Ladditional images of the input
spectrum distort the original spectrum. Therefore, a low
pass filter)(zH is used after the up-sampler removes
these additional images and also fills the zero samples
with non-ze ro values.
In this design, the Kalman filter is updated at every
100Hz and the tracking loops are updated at every 1 KHz.
Therefore, an interpolation factor of 10 is required to
convert the Doppler rate to 1000 Hz. As a first step, the
upsampler inserts nine zeros between two successive
input Doppler samples to increase the sampling rate, and
then a Remez lowpass filter is used to remove the images
caused by the upsampler. The input and output of
upsampler is shown in Figure 3.
The distorted output is due to the insertion of zero
samples. To remove this distortion and to smooth the
output spectrum, an FIR Remez filter with a length of 80
samples was designed. The transfer function of the filter
is given as
⎪
⎩
⎪
⎨
⎧
≤≤
≤
=
ππ wL
LwwL
eH c
jw
/,0
,/,
)( (8)
Fig. 3 Input and Output of Up Sampler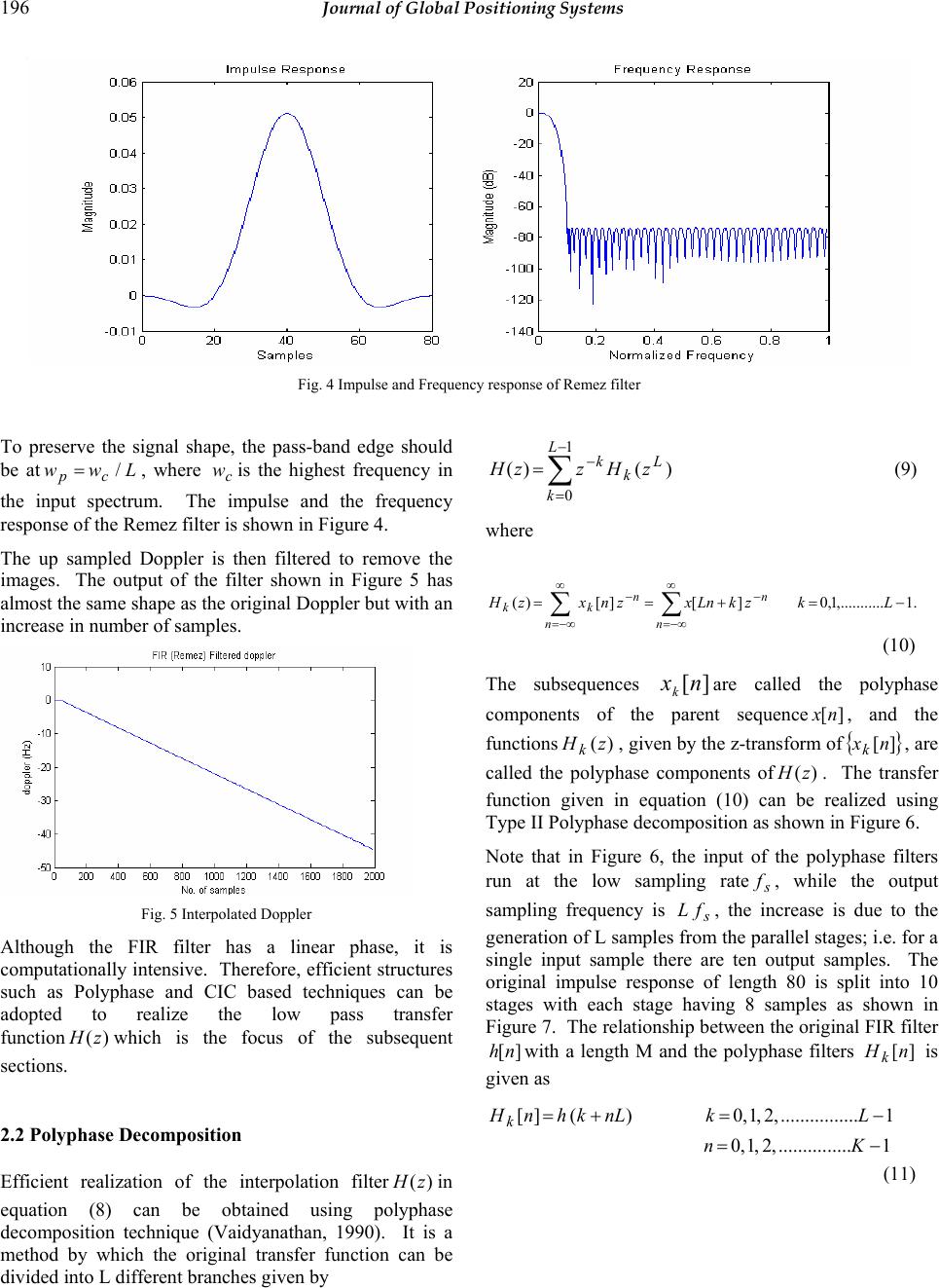

196 Journal of Global Positioning Systems
Fig. 4 Impulse and Frequency response of Remez filter
To preserve the signal shape, the pass-band edge should
be atLww cp /=, where c
wis the highest frequency in
the input spectrum. The impulse and the frequency
response of the Remez filter is shown in Figure 4.
The up sampled Doppler is then filtered to remove the
images. The output of the filter shown in Figure 5 has
almost the same shape as the original Doppler but with an
increase in number of samples.
Fig. 5 Interpolated Doppler
Although the FIR filter has a linear phase, it is
computationally inten sive. Therefore, efficient structures
such as Polyphase and CIC based techniques can be
adopted to realize the low pass transfer
function )(zH which is the focus of the subsequent
sections.
2.2 Polyphase Decomposition
Efficient realization of the interpolation filter)(zH in
equation (8) can be obtained using polyphase
decomposition technique (Vaidyanathan, 1990). It is a
method by which the original transfer function can be
divided into L different branches given by
∑
−
=
−
=
1
0
)()( L
k
L
k
kzHzzH (9)
where
.1..,.........1,0][][)( −=+==∑∑
∞
−∞=
∞
−∞=
−− LkzkLnxznxzH
nn
nn
kk
(10)
The subsequences ][nxkare called the polyphase
components of the parent sequence][nx , and the
functions )(zHk, given by the z-transform of
{} ][nxk, are
called the polyphase components of)(zH . The transfer
function given in equation (10) can be realized using
Type II Polyphase decomposition as shown in Figure 6.
Note that in Figure 6, the input of the polyphase filters
run at the low sampling rates
f, while the output
sampling frequency is s
fL , the increase is due to the
generation of L samples from the parallel stages; i.e. for a
single input sample there are ten output samples. The
original impulse response of length 80 is split into 10
stages with each stage having 8 samples as shown in
Figure 7. The relationship between the original FIR filter
][nh with a length M and the polyphase filters ][nHk is
given as
1...............,2,1,0
1................,2,1,0)(][
−=
−=+=
Kn
LknLkhnHk
(11)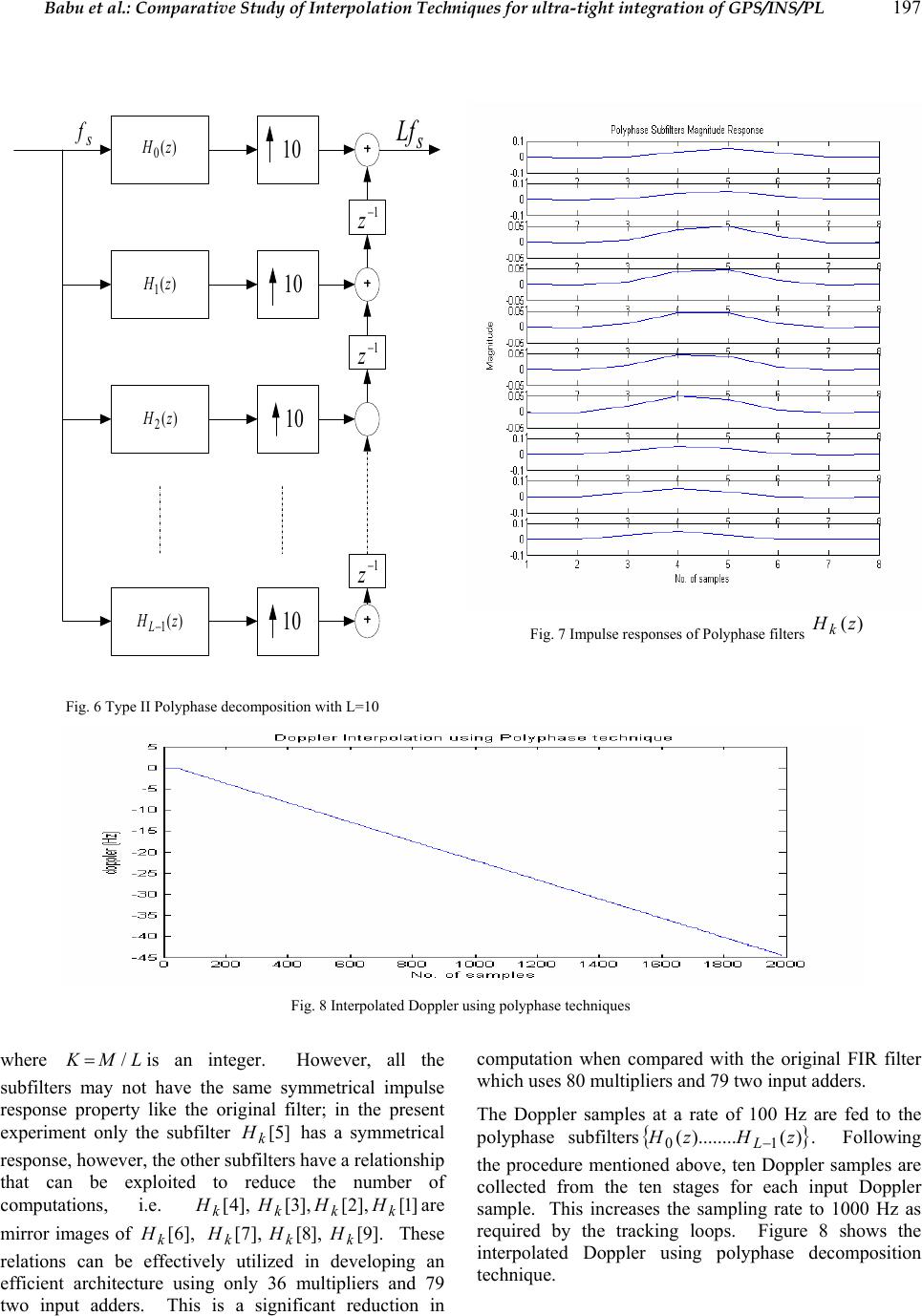

Babu et al.: Comparative Study of Interpolation Techniques for ultra-tight integration of GPS/INS/PL 197
Fig. 6 Type II Polyphase decomposition with L=10
Fig. 7 Impulse responses of Polyphase filters )(zHk
Fig. 8 Interpolated Doppler using polyphase techniques
where LMK/=is an integer. However, all the
subfilters may not have the same symmetrical impulse
response property like the original filter; in the present
experiment only the subfilter ]5[
k
H has a symmetrical
response, however, the other subfilters have a relationship
that can be exploited to reduce the number of
computations, i.e. ]1[],2[],3[],4[ kkkkHHHH are
mirror images of ],6[
k
H],7[
k
H],8[
k
H].9[
k
H These
relations can be effectively utilized in developing an
efficient architecture using only 36 multipliers and 79
two input adders. This is a significant reduction in
computation when compared with the original FIR filter
which uses 80 multipliers and 79 two input adders.
The Doppler samples at a rate of 100 Hz are fed to the
polyphase subfilters
{
}
)()........( 10zHzH L−. Following
the procedure mentioned above, ten Doppler samples are
collected from the ten stages for each input Doppler
sample. This increases the sampling rate to 1000 Hz as
required by the tracking loops. Figure 8 shows the
interpolated Doppler using polyphase decomposition
technique.
)(
0
zH
10
)(
1
zH
10
)(
2
zH
10
)(
1
zH
L−
10
1−
z
1−
z
1−
z
s
Lf
s
f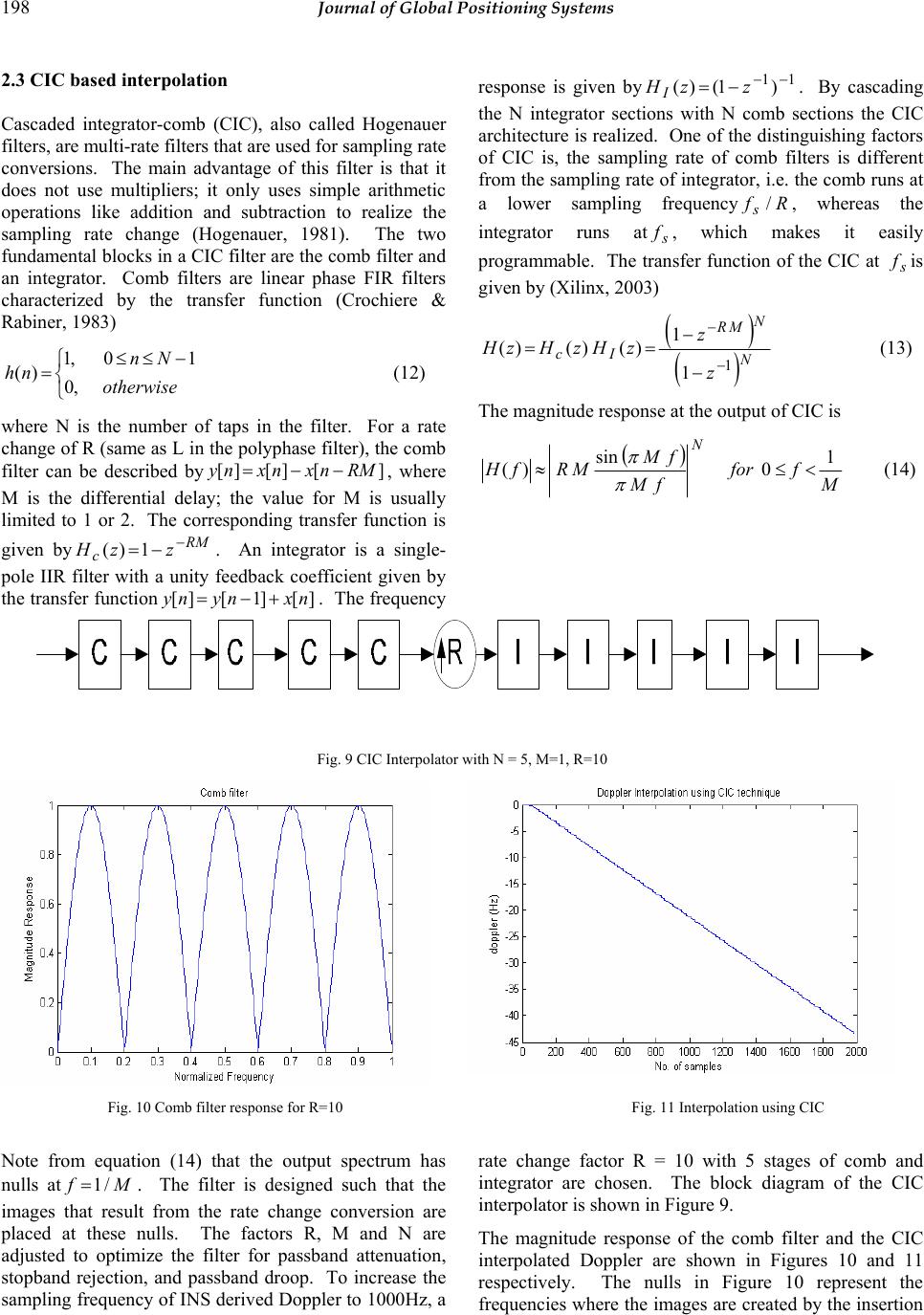

198 Journal of Global Positioning Systems
2.3 CIC based interpolation
Cascaded integrator-comb (CIC), also called Hogenauer
filters, are multi-rate filters that are used for sampling rate
conversions. The main advantage of this filter is that it
does not use multipliers; it only uses simple arithmetic
operations like addition and subtraction to realize the
sampling rate change (Hogenauer, 1981). The two
fundamental blocks in a CIC filter are the comb filter and
an integrator. Comb filters are linear phase FIR filters
characterized by the transfer function (Crochiere &
Rabiner, 198 3)
⎩
⎨
⎧−≤≤
=otherwise
Nn
nh ,0
10,1
)( (12)
where N is the number of taps in the filter. For a rate
change of R (same as L in the polyphase filter), the comb
filter can be described by][][][ RMnxnxny −−
=
, where
M is the differential delay; the value for M is usually
limited to 1 or 2. The corresponding transfer function is
given byRM
czzH −
−=1)( . An integrator is a single-
pole IIR filter with a unity feedback coefficient given by
the transfer function][]1[][ nxnyny +
−
=. The frequency
response is given by11)1()( −− −= zzHI. By cascading
the N integrator sections with N comb sections the CIC
architecture is realized. One of the distinguishing factors
of CIC is, the sampling rate of comb filters is different
from the sampling rate of integrator, i.e. the co mb runs at
a lower sampling frequencyRfs/, whereas the
integrator runs ats f, which makes it easily
programmable. The transfer function of the CIC at s
fis
given by (Xilinx, 2003)
(
)
()
N
N
MR
Ic z
z
zHzHzH 1
1
1
)()()( −
−
−
−
== (13)
The magnitude response at the output of CIC is
()
M
ffor
fM
fM
MRfH
N1
0
sin
)( <≤≈
π
π
(14)
Fig. 9 CIC Interpolator with N = 5 , M=1, R=10
Fig. 10 Comb filter response for R=10 Fig. 11 Interpolation using CIC
Note from equation (14) that the output spectrum has
nulls atMf /1=. The filter is designed such that the
images that result from the rate change conversion are
placed at these nulls. The factors R, M and N are
adjusted to optimize the filter for passband attenuation,
stopband rejection, and passband droop. To increase the
sampling frequency of INS derived Doppler to 1000Hz, a
rate change factor R = 10 with 5 stages of comb and
integrator are chosen. The block diagram of the CIC
interpolator is shown in Figure 9.
The magnitude response of the comb filter and the CIC
interpolated Doppler are shown in Figures 10 and 11
respectively. The nulls in Figure 10 represent the
frequencies where the images are created by the insertion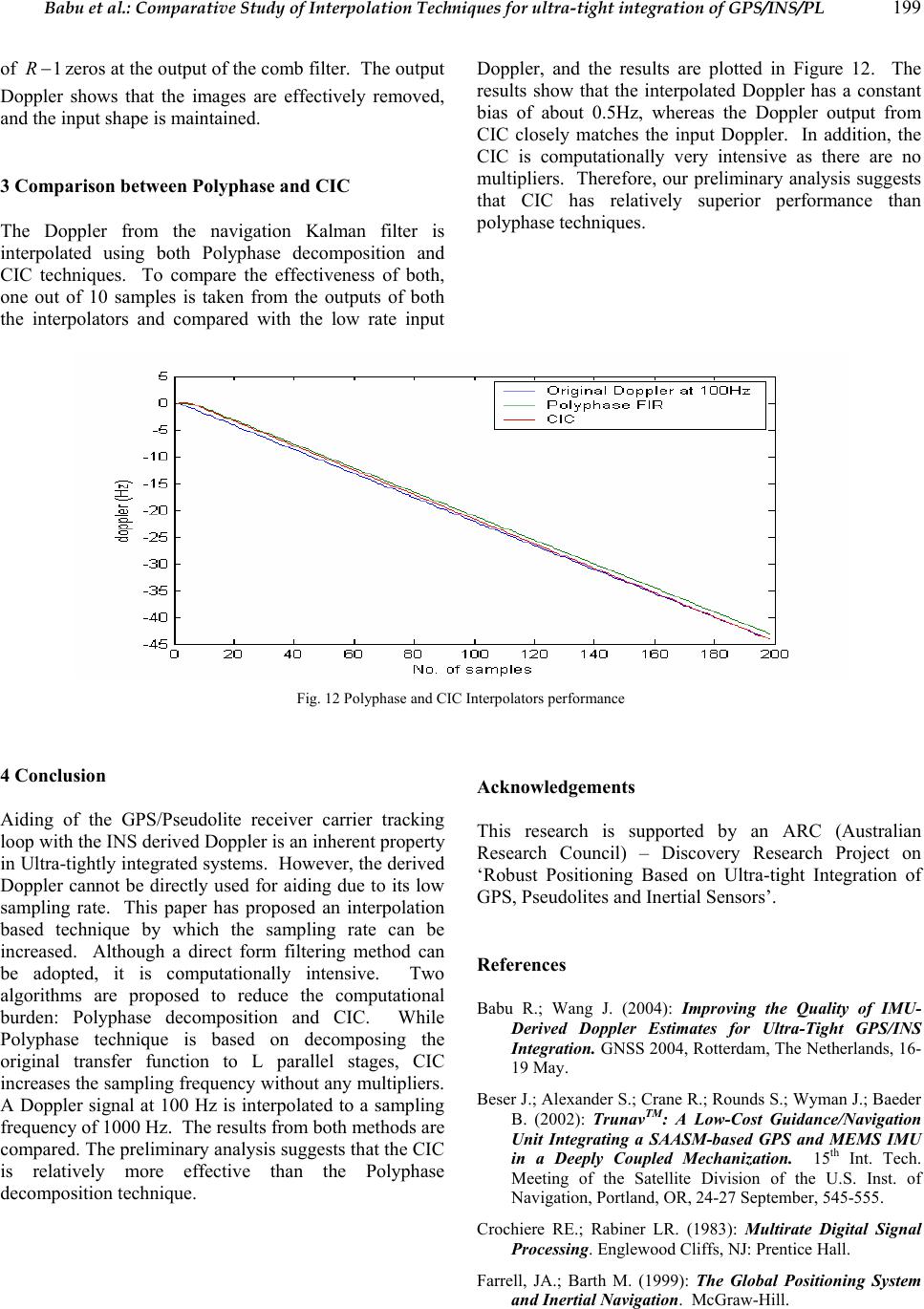

Babu et al.: Comparative Study of Interpolation Techniques for ultra-tight integration of GPS/INS/PL 199
of 1−Rzeros at the output of the comb filter. The output
Doppler shows that the images are effectively removed,
and the input shape is maintai ned.
3 Comparison between Polyphase and CIC
The Doppler from the navigation Kalman filter is
interpolated using both Polyphase decomposition and
CIC techniques. To compare the effectiveness of both,
one out of 10 samples is taken from the outputs of both
the interpolators and compared with the low rate input
Doppler, and the results are plotted in Figure 12. The
results show that the interpolated Doppler has a constant
bias of about 0.5Hz, whereas the Doppler output from
CIC closely matches the input Doppler. In addition, the
CIC is computationally very intensive as there are no
multipliers. Therefore, our preliminary analysis suggests
that CIC has relatively superior performance than
polyphase techniques.
Fig. 12 Polyphase and CIC Interpolators performance
4 Conclusion
Aiding of the GPS/Pseudolite receiver carrier tracking
loop with the INS derived Doppler is an inherent property
in Ultra-tightly integrated systems. However, the derived
Doppler cannot be directly used for aiding due to its low
sampling rate. This paper has proposed an interpolation
based technique by which the sampling rate can be
increased. Although a direct form filtering method can
be adopted, it is computationally intensive. Two
algorithms are proposed to reduce the computational
burden: Polyphase decomposition and CIC. While
Polyphase technique is based on decomposing the
original transfer function to L parallel stages, CIC
increases the sampling frequency without any multipliers.
A Doppler signal at 100 Hz is interpolated to a sampling
frequency of 1000 Hz. The results from both methods are
compared. The preliminary analysis suggests that the CIC
is relatively more effective than the Polyphase
decomposition technique.
Acknowledgements
This research is supported by an ARC (Australian
Research Council) – Discovery Research Project on
‘Robust Positioning Based on Ultra-tight Integration of
GPS, Pseudolites and Inertial Sensors’.
References
Babu R.; Wang J. (2004): Improving the Quality of IMU-
Derived Doppler Estimates for Ultra-Tight GPS/INS
Integration. GNSS 2004, Rotterdam, The Netherlands, 16-
19 May.
Beser J.; Alexander S.; Crane R.; Rounds S.; Wyman J.; Baeder
B. (2002): TrunavTM: A Low-Cost Guidance/Navigation
Unit Integrating a SAASM-based GPS and MEMS IMU
in a Deeply Coupled Mechanization. 15
th Int. Tech.
Meeting of the Satellite Division of the U.S. Inst. of
Navigation, Portland, OR, 24-27 September, 545- 555.
Crochiere RE.; Rabiner LR. (1983): Multirate Digital Signal
Processing. Englewood Cliffs, NJ: Prentice Hall.
Farrell, JA.; Barth M. (1999): The Global Positioning System
and Inertial Navigation. McGraw-Hill.

200 Journal of Global Positioning Systems
Gardner FM. (1993): Interpolation in Digital Modems – Part I:
Fundamentals. IEEE Transactions on Communications,
COM-41(3), 501-507.
Hentschel T.; Fettweis G. (2000): Sample Rate Conversion for
Software Radio. IEEE Communications Magazine,
August, 2-10.
Hogenauer EB. (1981): An Economical Class of Digital Filters
for Decimation and Interpolation. IEEE Transactions on
Acoustics, Speech and Signal Processing, Vol. ASSP-29,
155-162.
Kaplan ED. (1996): Understanding GPS: Principles and
Applications. Artech House, MA.
Mitra SK. (1999): Digital Signal Processing – A Computer
Based Approach. Tata McGraw-Hill Edition, India, ISBN
0-07-463723-1.
Tsui JBY. (2000): Fundamentals of Global Positioning
Receivers – A Software Approach. John Wiley & Sons,
Inc.
Vaidyanathan PP. (1990): Multirate Digital Filter, Filter
Banks, Polyphase Networks, and Applications: A
Tutorial. Proc. IEEE, 78, 56-93.
Vesma J. (1999): Optimizations and Applications of
Polynomial-Based Interpolation Filters. PhD Thesis,
Tempere University of Technology, Finland, ISBN 952-
15-0206-1.
Wang J.; Dai L.; Tsuiji T.; Rizos C.; Grejner-Brzezinska D.;
Toth C. (2001): GPS/INS/Pseudolite Integration:
Concepts, Simulation and Testing. 14th Int. Tech.
Meeting of the Satellite Division of the U.S. Inst. of
Navigation, Salt Lake City, Ohio, 11-14 September, 2708-
2715.
Ward P. (1998): Performance Comparisons Between FLL,
PLL and a Novel FLL-Assisted PLL Carrier Tracking
Loop Under RF Interference Conditions. 11th Int. Tech.
Meeting of the Satellite Division of the U.S. Inst. of
Navigation, Nashville, Tennessee, 15-18 September, 783-
795.
Xilinx. (2003): Digital Up Converter (DUC) DS276 v1.0
Product Specification.
(http://www.xilinx.com/ipcenter/catalog/logicore/docs/duc.
pdf).