Advances in Pure Mathematics
Vol.05 No.01(2015), Article ID:53153,3 pages
10.4236/apm.2015.51003
Upper Bound Estimation of Fractal Dimensions of Fractional Integral of Continuous Functions
Yongshun Liang
Faculty of Science, Nanjing University of Science and Technology, Nanjing, China
Email: liangyongshun@gmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 December 2014; revised 15 December 2014; accepted 1 January 2015
ABSTRACT
Fractional integral of continuous functions has been discussed in the present paper. If the order of Riemann-Liouville fractional integral is v, fractal dimension of Riemann-Liouville fractional inte- gral of any continuous functions on a closed interval is no more than 2 − v.
Keywords:
Box Dimension, Riemann-Liouville Fractional Calculus, Fractal Function

1. Introduction
In [1] , fractional integral of a continuous function of bounded variation on a closed interval has been proved to still be a continuous function of bounded variation. The upper bound of Box dimension of the Weyl-Marchaud fractional derivative of self-affine curves has given in [2] . Previous discussion about fractal dimensions of fractional calculus of certain special functions can be found in [3] [4] .
In the present paper, we discuss fractional integral of fractal dimension of any continuous functions on a closed interval.
If U is any non-empty subset of n-dimensional Euclidean space, 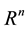 , the diameter of U is defined as
, the diameter of U is defined as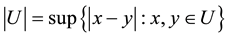 , i.e. the greatest distance apart of any pair of points in U. If
, i.e. the greatest distance apart of any pair of points in U. If 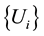 is a countable collection of sets of diameter at most δ that cover F, i.e.
is a countable collection of sets of diameter at most δ that cover F, i.e. 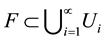 with
with 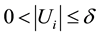 for each i, we say that
for each i, we say that 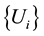 is a δ-cover of F.
is a δ-cover of F.
Suppose that F is a subset of 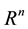 and s is a non-negative number. For any positive number define
and s is a non-negative number. For any positive number define
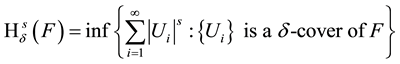
Write
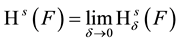
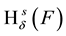 is called s-dimensional Hausdorff measure of F. Hausdorff dimension is defined as follows:
is called s-dimensional Hausdorff measure of F. Hausdorff dimension is defined as follows:
Definition 1.1 [5] Let F be a subset of 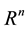 and s is a non-negative number. Hausdorff dimension of F is
and s is a non-negative number. Hausdorff dimension of F is
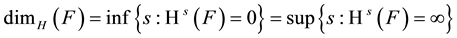
If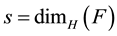 , then
, then 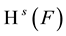 may be zero or infinite, or may satisfy
may be zero or infinite, or may satisfy
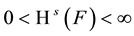
A Borel set satisfying this last condition is called an s-set.
Box dimension is given as follows:
Definition 1.2 [5] Let F be any non-empty bounded subset of  and let
and let 


and

If (1.1) and (1.2) are equal, we refer to the common value as Box dimension of F

Definition 1.3 [6] Let 


Riemann-Liouville integral of 
2. Riemann-Liouville Fractional Integral of 1-Dimensional Fractal Function
Let 


2.1. Riemann-Liouville Fractional Integral of
Theorem 2.1 Let 


Proof. Since 
From Definition 1.3, we know
For any

2.2. Fractal Dimensions of Riemann-Liouville Fractional Integral of
Theorem 2.2 Let 

Proof. Let


For



If
We have
Let

If
If
We get
There exists a positive constant C, such that
If 


From (1.2) of Definition 1.2, we know
With Definition 1.1, we get the conclusion of Theorem 2.2.
This is the first time to give estimation of fractal dimensions of fractional integral of any continuous function on a closed interval.
Acknowledgements
Research is supported by NSFA 11201230 and Natural Science Foundation of Jiangsu Province BK2012398.
References
- Liang, Y.S. (2010) Box Dimension of Riemann-Liouville Fractional Integral of Continuous Function of Bounded Vari- ation. Nonlinear Analysis Series A: Theory, Method and Applications, 72, 2758-2761.
- Yao, K. and Liang, Y.S. (2010) The Upper Bound of Box Dimension of the Weyl-Marchaud Derivative of Self-Affine Curves. Analysis Theory and Application, 26, 222-227. http://dx.doi.org/10.1007/s10496-010-0222-9
- Liang, Y.S. and Su, W.Y. (2011) The Von Koch Curve and Its Fractional Calculus. Acta Mathematic Sinica, Chinese Series [in Chinese], 54, 1-14.
- Zhang, Q. and Liang, Y.S. (2012) The Weyl-Marchaud Fractional Derivative of a Type of Self-Affine Functions. Ap- plied Mathematics and Computation, 218, 8695-8701. http://dx.doi.org/10.1016/j.amc.2012.01.077
- Falconer, J. (1990) Fractal Geometry: Mathematical Foundations and Applications. John Wiley Sons Inc., New York.
- Oldham, K.B. and Spanier, J. (1974) The Fractional Calculus. Academic Press, New York.




















