Journal of Applied Mathematics and Physics Vol.02 No.13(2014),
Article ID:52435,5 pages
10.4236/jamp.2014.213135
A Survey of the Implementation of Numerical Schemes for the Heat Equation Using Forward Euler in Time
Pedro Pablo Cárdenas Alzate
Department of Mathematics, Universidad Tecnológica de Pereira, Pereira, Colombia
Email: ppablo@utp.edu.co
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 September 2014; revised 17 October 2014; accepted 22 October 2014
ABSTRACT
We establish the conditions for the compute of the Global Truncation Error (GTE), stability restriction on the time step and we prove the consistency using forward Euler in time and a fourth order discretization in space for Heat Equation with smooth initial conditions and Dirichlet boundary conditions.
Keywords:
Global Truncation, Forward Euler, Heat Equation

1. Introduction
In this paper we have considered the heat equation
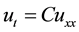 on
on
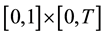 with smooth initial conditions and Dirichlet boundary conditions
with smooth initial conditions and Dirichlet boundary conditions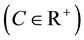 . Using forward Euler in time and fourth order discretization
in
. Using forward Euler in time and fourth order discretization
in
space, we compute the Global Truncation Error (GTE), the stability restriction on
the time step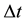 ,
also we prove consistency and finally we prove the convergence for this scheme.
,
also we prove consistency and finally we prove the convergence for this scheme.
Much attention has been paid to the development, analysis and implementation of
accurate methods for the numerical solution of this problem in the literature. Many
problems are modeled by smooth initial conditions and Dirichlet boundary conditions.
A number of procedures have been suggested (see, for instance [1] - [3] ). We can
say that three classes of solution techniques have emerged for solution of PDE:
the finite difference techniques, the finite element methods and the spectral techniques.
The last one has the advantage of high accuracy attained by the resulting discretization
for a given number of nodes [4] - [7] . Let
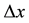 denote the grid-size in the spatial direction and
denote the grid-size in the spatial direction and
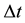 the gridsize in the time direction. By using forward Euler in time, and the fourth
order discretization from the previous problem in space, the heat equation reads:
the gridsize in the time direction. By using forward Euler in time, and the fourth
order discretization from the previous problem in space, the heat equation reads:
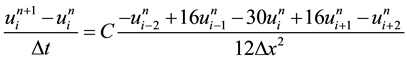 (1)
(1)
We’ll assume that the discretizations used near the boundaries have the same order [8] and [9] .
2. Global Truncation Error (GTE)
There are three equivalent ways of computing the Global Truncation Error for this case.
Way 1. We can always go back to the definition of the GTE. Let
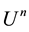 be the true solution at stage
be the true solution at stage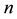 , and
, and
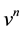 be the solution returned by the scheme at stage
be the solution returned by the scheme at stage . Therefore
. Therefore
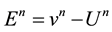 (2)
(2)
We consider de LTE
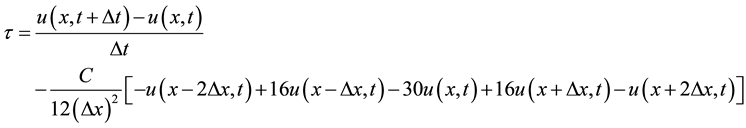 (3)
(3)
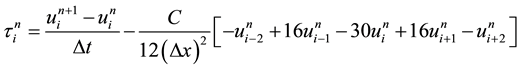 (4)
(4)
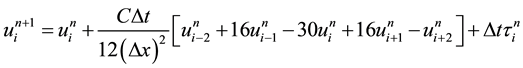 (5)
(5)
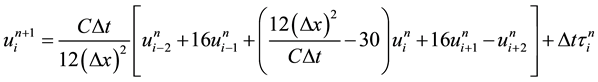 (6)
(6)

So that at stage

where




we get at stage


...


We now wish to estimate this quantity: first using the triangle inequality, we get

Now, taking stability into account, we can see that




Now, assuming that initial error is not too large, we have

Finally, we can conclude that the
Way 2. The GTE can be estimated by computing the LTE


Way 3. We can also compute the one-step-error for the scheme. This quantity is basically
equal to



then substitute the true solution and compute the difference of the two sides

We can then estimate the GTE by summing up the one-step error at each stage


3. Stability Restriction
We start by computing the stability restriction one has to impose on







then

Now, let


So that










4. Consistency and Convergence
We know that a discretization scheme [10] for a PDE is consistent provided that





Thus,



Lastly, since we proved that the scheme is consistent and stable, by Lax equivalence
theorem, we prove that the scheme is convergent. (By the above, since the GTE is

Another way to get the one-step error for the scheme is to combine the LTE for the temporal and spatial discretization, as follows.
LTE for forward Euler is




This is equivalent to the previous method for getting the one-step error.
Acknowledgements
I would like to thank the referee for his valuable suggestions that improved the presentation of this paper and my gratitude to Department of Mathematics of the Universidad Tecnológica de Pereira (Colombia) and the group GEDNOL.
References
- Strikwerda, J.C. (1989) Finite Difference Schemes and Partial Differential Equations. Wadsworth & Brooks, USA.
- McRea, G.J. and Godin, W.R. (1967) Numerical Solution of Atmospheric Diffusion for Chemically Reacting Flows. Journal of Computational Physics, 77, 1-42.
- Hundsdorfer, W. and Koren, B. (1995) A Positive Finite-Difference Advection Scheme Applied on Locally Refined Grids. Journal of Computational Physics, 117, 35-36. http://dx.doi.org/10.1006/jcph.1995.1042
- Morton, K.W. (1980) Stability of Finite Difference Approximations to a Diffusion-Convection Equation. International Journal for Numerical Methods Engineering, 15, 677-683. http://dx.doi.org/10.1002/nme.1620150505
- Canuto, C. and Hussaini, M. (1988) Spectral Methods in Fluids Dynamics. Springer Series in Computational Physics, Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-3-642-84108-8
- Dehghan, M. (2005) On the Numerical Solution of the One-Dimensional Convection-Diffusion Equation. Mathematical Problems in Engineering, 1, 61-74.
- Dehghan, M. (2007) The One-Dimensional Heat Equation Subject to a Boundary Integral Specification. Chaos, Solitons & Fractals, 32, 661-675. http://dx.doi.org/10.1155/MPE.2005.61
- Mitchell, A.R. and Griffiths, D.F. (1980) The Finite Difference Method in Partial Differential Equations. John Wiley & Sons, Chichester.
- Mickens, R.E. (2000) Applications of Nonstandard Finite Differences Schemes. World Scientific Publishing, River Edge.
- Lu, X., et al. (2005) A New Analytical Method to Solve the Heat Equation for a Multi-Dimensional Composite Slab. Journal of Physics, 38, 2873. http://doi:10.1088/0305-4470/38/13/004



