ABSTRACT

Classical simulation of a quantum system is a hard problem. It’s known that these problems can be solved efficiently by using quantum computers. This study demonstrates the simulation of the molecular Hamiltonian of 2p-π electrons of ethylene in order to calculate the ground state energy. The ground state energy is estimated by an iterative phase estimation algorithm. The ground state is prepared by the adiabatic state preparation and the implementation of the procedure is carried out by numerical simulation of two-qubit NMR quantum simulator. The readout scheme of the simulator is performed by extracting binary bits via NMR interferometer.

1. Introduction

Quantum information processing has become one of the most interesting fields in science and technology [1]. It has a potential to change the technology towards to quantum technology [2]. In 1982, Feynman proposed that simulation of quantum systems can be efficiently achieved by using computers working with the quantum mechanical principles [3]. First David Deutsch considered a computer device based on quantum mechanical principles [4]. Then other experimental and theoretical studies are performed on quantum information processing [5,6]. Seth Lloyd defined quantum computers as universal quantum simulators by recalling Feynman’s original motivation for introducing quantum computers [7]. The classification of quantum simulation is separated into two main lines. One of them is simulating a target quantum system by using another quantum system and the latter is simulating the target quantum system by constructing the elements of the target Hamiltonian with unitary and universal quantum logic gates [8].

With mature quantum control methods, NMR is an excellent test bed of physical implementations of quantum computing. Some physical systems examined by quantum simulations in the framework of NMR methods are reported elsewhere [9-13]. For quantum chemistry problems many approximation methods and software packages are developed since the difficulty of the problem scales exponentially with the system size. But it’s known that quantum computers promise efficient algorithms in order to simulate and prepare quantum states and find eigenvalues in polynomial time [14,15]. In order to calculate molecular energies, phase estimation algorithm is used by Guzik et al. [16]. In this algorithm the energy information can be extracted by phase kick-backs. For eigenstate preparations, Adiabatic State Preparation (ASP) is also proposed by Guzik et al. [16]. ASP exploits the quantum adiabatic theory in order to simulate the ground state of the desired system. Once the ground state is prepared, the ground state energy information can be extracted via relative phases by the phase estimation procedure. Recent studies about quantum simulations of quantum chemistry problems can be found elsewhere [18-23]. For experimental implementations, iterative phase estimation algorithm (IPEA) is developed in order to reduce the number of qubits [24]. NMR techniques provide efficient ways to optimize the adiabatic procedure for ground state preparation [25].

This study performs a numerical simulation of the quantum simulation of 2p-p electronic Hamiltonian in molecular ethylene on an NMR quantum computer. In quantum simulation an iterative phase estimation algorithm (IPEA) is used for the calculation of the ground state energy [24]. Ground state is prepared by ASP [25]. The goal of this study is to present a quantum simulation procedure for a better understanding of IPEA and ASP algorithms with NMR techniques. This manuscript is organized as follows. Section 2 explains a brief introduction to the theory about the problem Hamiltonian and the ground state energy calculation process. Definition of the problem and it’s solution methods can be found in Section 3. Results and discussion are presented in Section 4. Conclusion of the study is given in Section 5.

2. Theory

The aim of classical simulation of a system is to obtain the final state by solving the differential equations which governs the dynamical behaviors of the system with known initial conditions. Since the number of differential equations increase exponentially with the system size, it’s inefficient to simulate quantum systems with classical computers.

The goal of quantum simulation is to use quantum systems to simulate other quantum systems in order to achieve the simulation process efficiently. The evolutions of quantum systems are expressed by the second postulate of quantum mechanics as

(1)

Where is the  system Hamiltonian. The challenge of quantum simulation is to discrete the system hamiltonian by a set of unitary operators as

(2)

Where is the total time of simulation process. Generally is hard to exponentiate and first, second or higher orders of approximations are possible for splitting the operator [1].The energy forstate which is prepared by a universal quantum computer can be obtained by a phase estimation algorithm [14,16]. The unitary operator is applied as a controlled fashion to 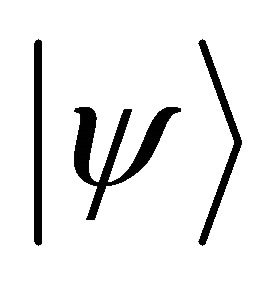in the target register:

(3)

Where is an eigenstate of. In the eigenvalue equation above, energy is encoded in phase as

(4)

Where t can be chosen arbitrarily in which ranges from 0 to 1. Finally an inverse quantum Fourier transform is applied the first register before the measurement process [16].

2.1. The Hamiltonian

For the molecular Hamiltonian of ethylene 2p-π electrons, we adopt the notation used elsewhere [26]:

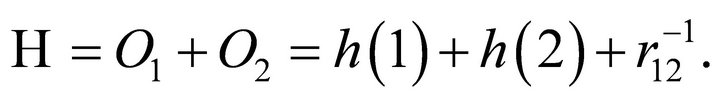(5)

Where 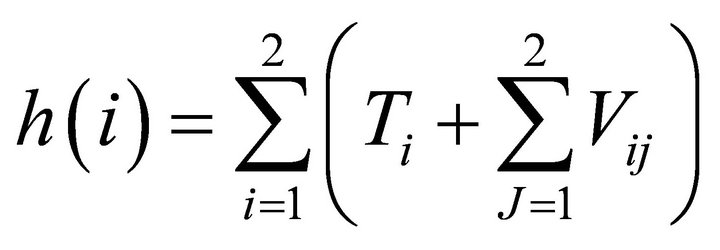is the core Hamiltonian for

electron and is the coulomb potential energy between two electrons.

To obtain the Hamiltonian and calculate electronic energies as functions of configuration, we choose a truncated basis set which is a standard approach for quantum chemistry calculations. In our simple case we don’t need Hartree-Fock procedure to determine spin orbitals because we obtain four spin orbitals by symmetry as

(6)

Where is the spatial function and and are spin functions. By using 4 spin orbitals and 2 electrons, there are different configurations. By evaluating the symmetry, just two determinants, ground state and doubly excited state appear in the calculations. As the first step of the simulation process the ground and the doubly exited states are mapped to computational basis as. By these considerations a Full Configuration Interaction (FCI) Hamiltonian matrix is [26]

(7)

Where and are one electron integrals, exchange integrals and coulomb integrals respectively.

2.2. IPEA and the State Preparation

IPEA is used to reduce the number of qubits and operations in obtaining the eigenvalues. The form of an IPEA is presented in Figure 1 [24]. The information will be extracted by the top qubit which is prepared as and the lower one prepared as which is the eigenstate wave function of. The unitary operation is applied as controlled operation and it obeys Equation (1). For a two qubit example after hadamard and controlled operations, the state becomes

(8)

Where implies the hadamard operation in the first qubit and the phase is defined in the binary ex-

pansion as 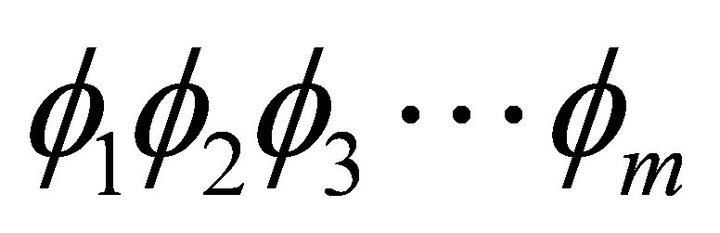with no more than m bits. In the first iteration, the gate is applied and bit is extracted deterministically. Then bit is extracted by the next iteration. This iteration is performed by the previous bit information and a conjugated Z rotation with the angle of Information is transferred through this rotation which is called a feedback operation. So the less significant bits are extracted first and then by evaluating the extracted information more significant bits are obtained.

The ground state wave function can be prepared by some number of operations by exploiting adiabatic theorem. According to adiabatic theorem, the system will remain in its ground state if the Hamiltonian varies slowly enough and if there is a gap between the ground state and the first excited state [17]. The adiabatic evolution of the Hamiltonian as a function of implementation steps (m) can be stated as [25]

(9)

Where 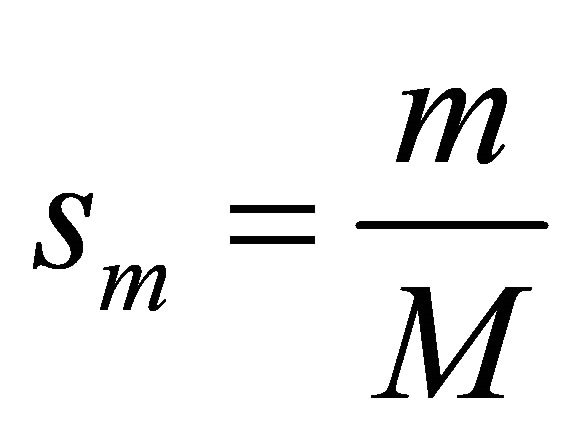and M is the number of steps, is the initial Hamiltonian and 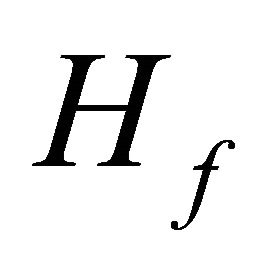is the problem Hamiltonian. For a realistic operator implementation of this Hamiltonian as, one can use TrotterSuzuki Formulato parse the steps as;

[1]. Where, is the total time of the adiabatic evolution and is the total number of steps.

3. Ethylene 2p-π Electrons Problem

The FCI Hamiltonian matrix for ethylene 2p-π electrons can be constructed by evaluating the integrals indicated above. The elements of the problem matrix can be constructed as and in a.u. [27]. The problem is to present the calculation of the ground state energy of the Hamiltonian by a two qubit NMR quantum computer. The calculated result can be compared with the theoretical one which is the lowest eigenvalue of the problem matrix. Chloroform molecule was chosen as two-qubit NMR quantum register and initialized for the experiment [28,29]. Here, proton nucleus is assumed to be the probe qubit in which the energy information will be extracted. And the carbon nucleus is the system qubit in which the simulation will take place.

The calculation procedure will be carried out by an IPEA as seen in Figure 1. Here we see a controlled operation where acts on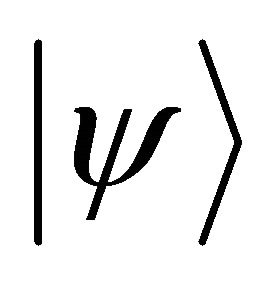. is the ground state of ethylene 2p-π electrons system and is the system hamiltonian. The energy information will be encoded by the extracted phase by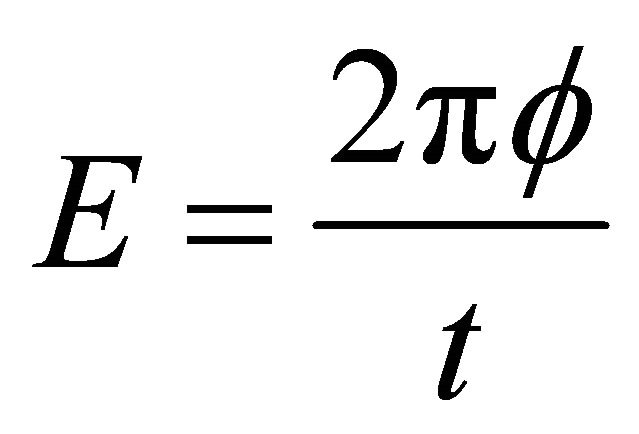. We obtain this phase by eigenvalue equation. To justify this equation the ground state of the system should be prepared before the controlled operation. Then the first step of the problem is to prepare the ground state of the system. As addressed before, ASP procedure will be used to prepare the ground state. The ASP process will be carried out by NMR techniques [25]. According to the ASP process, the initial Hamiltonian should be altered slowly towards target Hamiltonian by Equation (9). The target hamiltonian can be obtained easily in terms of pauli operators by substituting the integral values given above into the problem matrix in Equation (7). On the other hand the initial state of the system qubit should be the superposition of the ground state and the doubly excited state 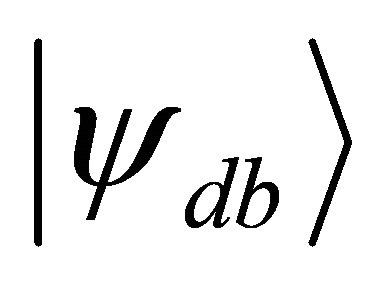as

to fulfill the initialization condition of the adiabatic process. This state can be obtained by applying a NMR pulse to the system qubit

which initially has a local natural Hamiltonian

. Thus the initial hamiltonian is.

Figure 2 illustrates ground state simulation of the system qubit. The evolution of the initial Hamiltonian to the final Hamiltonian should not be like a sudden jump as shown in Figure 2(a) but it should be a slow variation in which the adiabatic condition entails. This slow adiabatic variation of the system hamiltonian can be carried out by composite pulses which are well known by NMR platform [30].

Since the algorithm explained in Figure 1 will be implemented by an NMR quantum computer, all unitary operators should be carried out by radio frequency (rf) pulses. In order to construct the controlled operation in terms of rf pulses, the methods are adopted from elsewhere [30]. The ground state energy information of the system which is encoded in the relative phases should be extracted by binary digits since the computational bases

are in binary form. The binary phase information will be extracted by some number of iterations by IPEA. The extracted phase information should be converted to the corresponding decimal value. And then the obtained decimal value of the relative phase should be substituted into Equation (4) in order to obtain the ground state energy. The decimal value of the relative phase should be between 0 and 1 and we choose for simplicity.

4. Results and Discussion

In this study we concern with obtaining ground state energy by IPEA and simulating the ground state by ASP. Extracting the ground state energy information by a phase estimation algorithm has three main steps: 1) preparing the ground state wave function into qubits by an appropriate mapping, 2) processing controlled operations to extract information and 3) a measurement to readout the extracted information. By evaluating the integrals given in Equation (7), we have the following Hamiltonian matrix which is written in terms of Pauli operators as [27]

(10)

Here and. The theoretical ground state energy is −1.310 356 879 322 492. This value is obtained by diagonalisation of the Hamiltonian matrix. The circuit representation of the two qubit IPEA for calculating ground state energy of 2p-πelectrons in ethylene is shown in Figure 3.The numerical simulation of the proposed implementation is performed by Matlab program.

The Hamiltonian of the two qubit liquid state NMR quantum register is

(11)

Where and 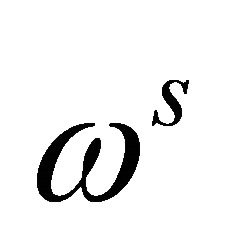are angular frequencies for the nuclei of the probe and the system qubits, respectively. The scalar coupling, is chosen as 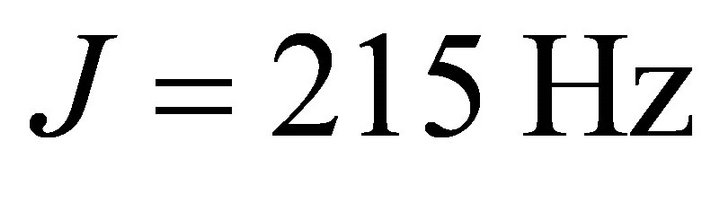which matches with the value for the Heteronuclear chloroform molecule[28]. The experiment starts with an initial deviation density matrix which is a pseudo pure state [29]. A rotation is applied by a pseudo Hadamard gate. And a conjugated rotation applied to the system qubit to start the ASP process. Thus, the initial Hamiltonian is and the problem Hamiltonian is by omitting 𝟙. The implementation of ASP is carried out by an operator [30]:

(12)

Here, and

.The overall time of the adiabatic process has its optimum value of 5 a.u. as indicated in Figure 4. In our demonstration, extracted information is three bits per iteration. Iteration is progressed from more significant bits to less significant ones, implying that iterations starts at. Thus is applied as controlled operation. NMR pulse sequence of the controlled operator is constructed in the operator form as [31]

(13)

In order to apply the gate as an NMR pulse sequence the third operator in the sequence can be written as [31]

(14)

The last step of the algorithm is the measurement of the phases. The phase shifts between two states can be read by a phase sensitive NMR spectrum. This readout scheme is referred as an NMR interferometer in which the bit information can be directly extracted from the relative phase measurements of the NMR spectrum [32]. The relative phase shifts (in degrees) after some powers of controlled operations and the extracted binary bits after some iterations are shown in Figure 5. Iterations are formulated as

(15)

Where and is the relative phase solely obtained from the powers of controlled operations. The relative phase obtained from the operations, which carry extracted bit information is depicted as. We choose 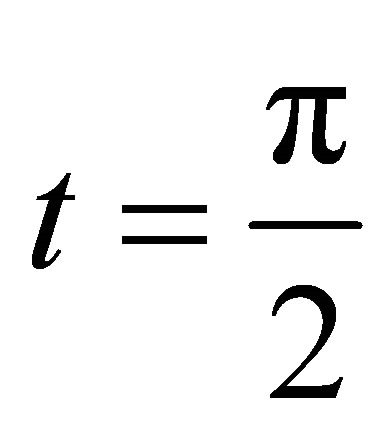to make Extracted binary bits were evaluated by Equation (15) and depicted as in Table 1. For instance, in the first iteration for 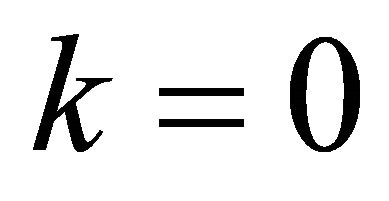the controlled operation is and after this operation obtained relative phase is 120 in degrees. And for we applied the controlled operation is and we had in degrees as shown in Figure 5. The first extracted bits for the first iteration were obtained via Equation (15) such that, where. Concisely the corresponding relative phase for the first iteration is in degrees. Corresponding phase factor can be obtained easily

by  such that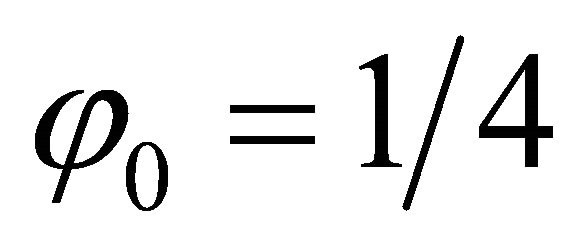 which corresponds to 010 in binary digits. Likewise in the second iteration, the extracted bits are 100 and so on.

After evaluating the extracted binary digits in decimal form, the ground state energy can be obtained from Equation (4). For instance after six iterations, the extracted phase is which corresponds to in decimal. By substituting this result into Equation (4) one obtains the energy value. This value has four bit accuracy with the theoretically calculated ground state energy. One can improve the energy value by going further iterations. But in a real experimental implementation, the accuracy of the simulation is limited by the experimental errors [33].

5. Conclusions

In this study, a quantum simulation algorithm is performed to calculate the ground state energy for 2p-π electrons of molecular planar ethylene with a classically simulated two-qubit NMR quantum register. The Hamiltonian of 2p-π electrons in ethylene is written in matrix form and the ground state and the doubly excited state configurations are mapped in the computational basis. A two qubit liquid state NMR Hamiltonian is proposed to perform the implementation as system Hamiltonian for classical simulation. A slightly modified IPEA algorithm is used for the simulation. Adiabatic state preparation is used to prepare system qubit as the ground state of the Hamiltonian in question. By the algorithm three bits are extracted per iteration and the extracted information is progressed from more significant bits to less significant bits. The corresponding decimal value of the phase which is obtained by the extracted bits, yields the energy information from Equation (2). The measurement of the probe qubit is performed by classically simulated phase sensitive NMR spectrum. The pseudo pure state of NMR spectrum is fixed as the reference spectrum throughout the experiment. Hence the quantum simulation of the ground state of 2p-π electrons in ethylene molecule is achieved by a two-qubit NMR quantum register. Also the robustness of the method is examined by comparing obtained ground state energy with the theoretical ground state energy.

REFERENCES

NOTES

^*Corresponding author.