Open Journal of Physical Chemistry
Vol.2 No.4(2012), Article ID:24697,8 pages DOI:10.4236/ojpc.2012.24028
A Graph-Theoretical Approach to Calculate Vibrational Energies of Atomic and Subatomic Systems
Department of Physical Chemistry, Faculty of Pharmacy, University of Valencia, Valencia, Spain
Email: jorge.galvez@uv.es
Received October 3, 2012; revised October 25, 2012; accepted November 11, 2012
Keywords: Graph Theory; Physical Systems; Vibrational Energy
ABSTRACT
One of the challenges still pending in string theory and other particle physics related fields is the accurate prediction of the masses of the elementary particles defined in the standard model. In this paper an original algorithm to assign graphs to each of these particles is proposed. Based on this mapping, we demonstrate that certain indices associated with the topology of the graph (graph theoretical indices) are very effective in predicting the masses of the particles. Specifically, the spectral moments of the graph adjacency matrix weighted by edge degrees play a key role in the excellent correlations found. Moreover, the same topological pattern is found in other well known quantum systems such as the particle in a box and the vibrational frequencies of diatomic molecules, such as hydrogen. The results shown here open a suggestive pathway for the use of graph-theoretical approaches in predicting properties of elementary particles and other physical systems, which seem to match similar topological patterns.
1. Introduction
Among the most important achievements generally recognized to string theory is its potential capability to predict the masses of elementary particles, specifically of the 12 particles that make up the three families of the standard model [1]. The process, however, require very complex mathematical calculations which are still far from complete.
There is a well known precedent in particle physics to the study of interactions between particles, which are the Feynman diagrams [2].

Figure 1. Feynman diagram for electron-positron annihilation. e: electron (–) or positron (+) q: quark γ = gamma emission.
Figure 1 shows the Feynman diagram for electron-positron annihilation.
It is interesting that, although representing a spacetime event, Feynman diagrams are ultimately graphs. A graph is a set of points called vertices (or nodes) connected by lines called edges. The studies of graphs constitute a discipline known as graph theory. It was L. Euler (1707- 1783) the one who introduced the notion of graph [3], which was developed later on by A. Cayley [4] and J. J. Sylvester [5] along the nineteenth century. In the 20th century, graph theory became an essential tool in different areas of science and technology where connectivity plays a role. Think, for instance, of the optimization of communication and transport networks [6], the design of electrical circuits (e.g. in computers) [7], the synchronization of interacting oscillators with different topologies [8], the analysis of social networks [9], among others.
Although graphs in general are also widely employed in theoretical physics, however graph-theoretical indices are rarely used [10]. Our goal here is just using graphtheoretical indices to predict the masses of the elementary particles referred above as well as of other physical systems such as molecular vibrational energy.
2. Assignation of Graphs to Some Vibratory Physical Systems. Theoretical Framework
Starting by the elementary particles, we must remind the origin of the Feynman diagrams. It is well known that the interactions between particles are expressed as an integral, which is typically too difficult to do, so that Feynman developed a perturbation theory which was based upon an expansion in terms of graphs. The type of such graphs depends on the interactions.
A similar approach can be also found in the so called force-based algorithms [11], in which the entire graph is then simulated as if it were a physical system, for example an elementary particle. Moreover, the use of graphs and matrices to study the interactions between elementary particles, for example quarks, has been also carried out by other authors [12].
On string theory, the way to explain that an elementary particle, say an electron, has a given mass is based on the different modes of vibration of the strings. Indeed, in the perturbative approach to string theory, the strings interact by joining and splitting [13].
Each vibrational mode has an associated energy according to Einstein’s equation:
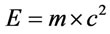 (1)
(1)
This energy is transformed into the elementary particle mass. In this sense we can say that elementary particles are made of strings.
In the perturbative string theory, the influence of each incoming string results from adding together the influences of graphs with ever more loops.
The algorithm proposed here is similar, i.e. assigning each perturbative term to each one of the particles so that each graph simply adds a loop over the next particle with increasing mass; in other words we propose assigning one-to-one the perturbative terms to the particles.
The process of assigning individual graphs to each elementary particle proposed here is done as follows: First, the elementary particles are sorted in increasing order of mass ranging from the electron-neutrino (<10–8) up to top-quark (189), both in GeVs. Table 1 reflects the values, in increasing order of energies, for these particles. On the first column is the allocation of families for every one of the particles. A data taken from reference [13].

Table 1. Elementary particles, according to the standard model, ordered in increasing values of energy. F1, F2 and F3 represent the three families in which they are classified.
For the first particle, namely electron-neutrino, we assign a simple graph that is equivalent to the interaction electron-positron described before.
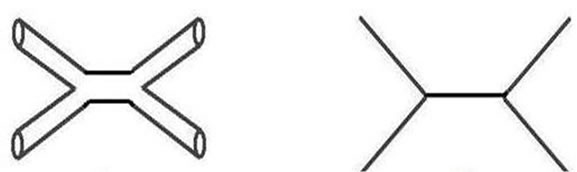 (a) (b)
(a) (b)
Figure 2. Allocation graph to electron-neutrino. Left (a) Feynman-like graph for the springs interaction and right; (b) corresponding simple graph.
Figure 2 illustrates the Feynman-like 3D diagram associated to the strings interaction, i.e. the string/antistring pair, together with the simple (no loops) graph assigned to it:
The following larger energy particles are represented by pseudographs which take into account different topologies with 1, 2, 3, ...11 holes. For example, for the muon-neutrino, the second lowest energy particle, we would have the following equivalence between the strings’ interaction and the graph (Figure 3):
 (a) (b)
(a) (b)
Figure 3. Allocation of graph to muon-neutrino, the second particle with lower mass. To the left (a) Feynman graph and on the right (b) corresponding pseudograph.
In this case, the two strings interact creating a hole whose graph theoretical equivalent is the one-loop graph on the right (B) of Figure 3. In short, the two diagrams in Figure 3 correspond to the Feynman representations for string (A) and quantum field theory (B) [14]. The advantage of this approach is that there is just one diagram for each order of perturbation and that each diagram avoid the drawback of short-distance infinities, i.e. contrary to quantum field theory, the graphs in Figures 2(a) and 3(a) have not singularities (nodes). It is also curious that the topological pattern that we meet here is the same as the one of harmonic vibrations of a macroscopic string (such as a violin string), in which each frequency of the overtones (n = 2, 3, 4…) is an integer multiple of the first one (n = 1, fundamental), as shown in Figure 4.

Figure 4. Simple modes of vibration of a string. The harmonic frequencies shown are multiples of the first one (fundamental vibration).
Note that the graph-theoretical equivalent of each mode of vibration would be graphs with a progressive increase in the number of loops.
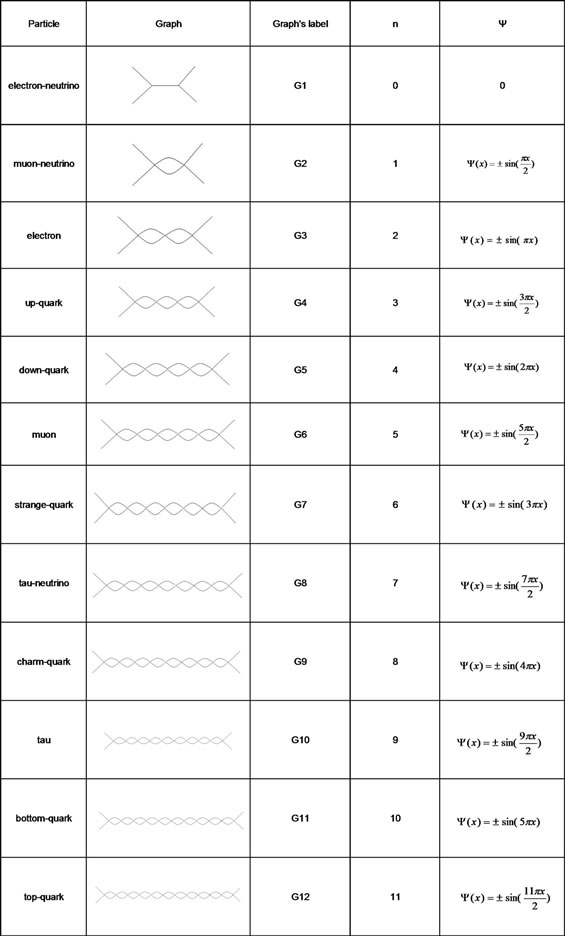
Figure 5. Allocation of graphs to different particles. On the right, the real part of wavefunctions for particle in a box for different quantum levels (n).
Figure 5 shows the graphs allocated to the different particles, according to our algorithm.
Except for the less massive particle, the electron-neutrino, which is assigned a simple graph, the rest are assigned on pseudographs with increasing number of adjacent loops.
Furthermore, the same graph allocation can be done on other quantum systems such as the particle in a box, whose wave functions (the real part) are also outlined in Figure 5 for the different quantum levels (n). These wave functions show a shape that is equivalent to the graphs assigned to each particle. This approach relating graphs to wavefunctions has been proposed previously by the author [15].
In fact, the proposed allocation of graphs can be based on very simple theoretical terms considering the vibrating strings as particles in a one-dimensional box and giving each particle a quantum number (n). Indeed, considering only the real part of the wave function associated with a one-dimensional box of length “a”, we have [16]:
 (2)
(2)
Which normalized for a = 2 leads to:
 (3)
(3)
It is clear from Equation (3) that the number of maxima-minima associated with the wave function is equal to the quantum number n, which can take the values 0, 1, 2, 3... The value 0 is associated to the ground state which corresponds to annihilation.
A similar result could be reached using the harmonic oscillator model, in which, for the one-dimensional case, the number of interior nodes on the boundary points is zero for the ground state and increases by one for each successive excited state, according to:
 (4)
(4)
where:


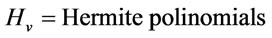 .
.
In this case there is a residual vibrational energy that would correspond to the lowest mass particle (electronneutrino), so that the association would be between the number of nodes and the number of loops in the graph. This way we can see that, regardless the model used, if we translate into graph-theoretical terms the wave functions, each graph has the same number of loops as number of singular points (maxima-minima or nodes) has the wave function. The relationship between wave functions and graphs is implicit in Heisenberg’s matrix formulation of quantum mechanics, because for each array or matrix a graph of connections can be assigned. Moreover, Filk has solidly demonstrated the equivalence between wave functions and graphs [17].
Within this theoretical framework, it is to be expected that the same allocation of graphs we have proposed for elementary particles, may also work in other physical systems, as for example, the vibrational energies of a diatomic molecule. In concrete we have applied this approach to predict the vibrational levels energy for the molecule of hydrogen. Given that in this case we have a residual vibrational energy for the lowest quantum level (v = 0), we assign the graphs G2, G3, G4, … to the first, second, third, ...vibrational levels, respectively.
3. Results and Discussion
After the allocation of the different graphs, the next step is to calculate the topological descriptors associated with each graph and try to establish a correlation with the energy of the particles. For calculation of topological descriptors, the software Dragon (a pull of some 330 indices) was used [18] and to obtain the regression equations, the BMDP statistical package [19] was run on the data.
The results clearly demonstrate that spectral moments are the variables that contribute most to the variance as for the correlation with the elementary particle masses.
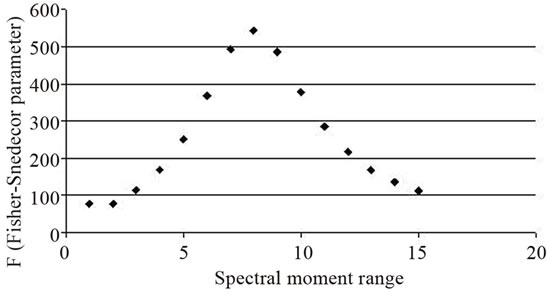
Figure 6. Representation of the values of Fisher-Snedecor parameter (F) as a function of the spectral moments.
Thus, Figure 6 illustrates the representation of the parameter F (Fisher-Snedecor) as a function of the spectral moments’ ranges (ordinals). As can be seen, in almost all cases the value is greater than 100, so demonstrating that the spectral moments play a key role in the predictive equation of the particle masses, being the #7 to #9 the major contributors to the variance (F around 500).
The best regression equations with one and two variables were:
 (5)
(5)
N = 12 R = 0.99095 SE = 0.3739 F = 545.1
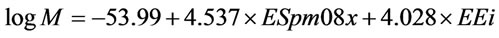 (6)
(6)
N = 12 R = 0.99684 SE = 0.2333 F=708.5 The symbols in Equations (5) and (6) are:
M = Particle mass (GeV)
ESpm08x = Spectral moment 08 from edge adjacency matrix weighted by edge degrees EEig11x = Eigenvalue 11 from edge adjacency matrix weighted by edge degrees.
N = Number of data R = Regression coefficient SE = Standard error of estimate F = Fischer-Snedecor parameter The spectral moments of the edge adjacency matrix are defined as the traces, i.e., the sum of the main diagonal entries, of the different powers of the matrix [20].
The k-th spectral moment of a graph G,  , with eigenvalues λ1, λ2 . . . , λn, is defined as:
, with eigenvalues λ1, λ2 . . . , λn, is defined as:
 (7)
(7)
It is to be noted that the spectral moment μk represents the number of weighted closed walks of length k existing in the graph, what makes the outcome from Equations (5) and (6) all the most reasonable considering the allocation of graphs done here. Moreover, both equations showed to be non-random and stable under the cross validation (leave-one-out) procedure. Interestingly, although both equations exceed 0.99 of correlation coefficient, the larger value of the parameter F (Fisher-Snedecor) as well as the significant drop in the standard error (from 0.37 to 0.23) in Equation (6), clearly shows that the two-variable equation is more significant.
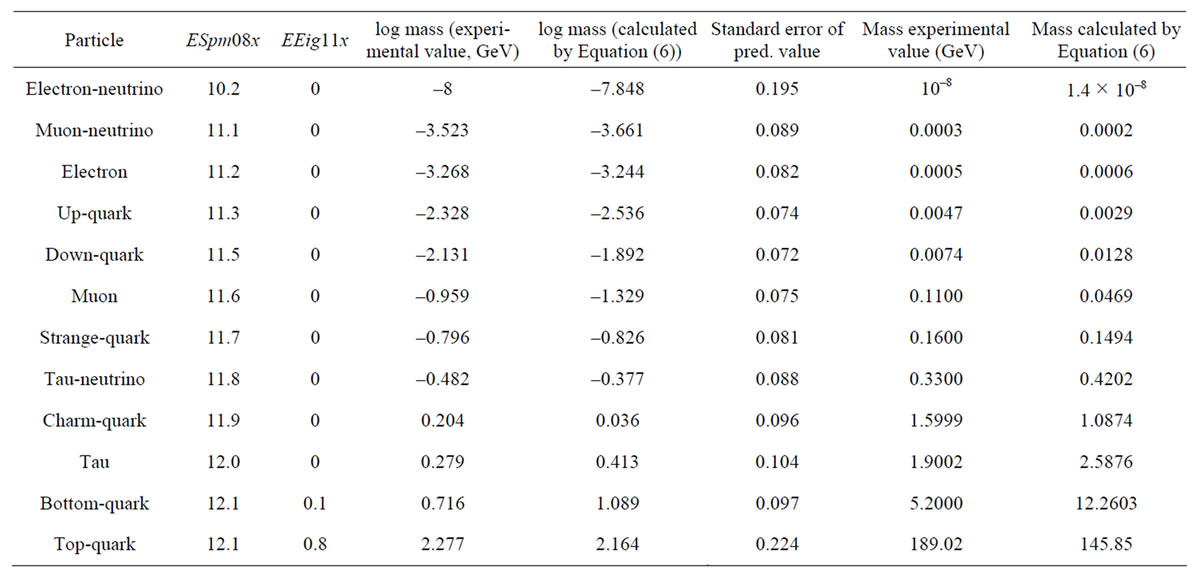
Table 2. Values of the topological indices together to the observed and calculated (Equation (6)) values of particle masses.
Table 2 illustrates the values of the two topological indices from the selected regression equation (ESpm08x and EEig11x) for each particle, as well as the comparison between the experimental and the calculated values from the two-variable equation in both, logarithmic and direct scale. As can be seen, the variable explaining most of the variance is ESpm08x, whereas the other, EEig11x, only improves the prediction for the two most massive particles (bottom and top quarks).
Furthermore, there is a good matching between the actual and the calculated values, what is to be emphasized given the simplicity of the procedure followed and the ease of calculation. It is also noteworthy the low standard errors achieved, which, except for the lowest and the highest value, are always below 0.1, i.e. 10%, what can be considered a significant achievement taking into account the wide range of magnitude of the particle energies.

Figure 7. Plot of the observed versus the calculated values of the particle masses according to Equation (6).
Figure 7 illustrates the plot of the experimental versus the calculated values. It is noteworthy the excellent agreement.
Interestingly, in both Equations (5) and (6), the indices therein are those derived from the edge adjacency matrices weighted by edge degrees, what accounts for the importance of interconnections between the nodes rather
<than that of the nodes themselves. Of course, this implies that, as expected, the topology associated with each particle plays a key role, beyond geometric characteristics related to size or shape. In particular the presence of successive adjacent loops stands as an essential element of the predictive, which is interpreted as successive stages of annihilation-splitting of the interacting strings.
It is also compelling that the great difference between the less massive particle (electron-neutrino) and the next one (muon-neutrino) is a pure “topological” gap because it is the difference between no-loop and one-loop graphs.
As pointed above, no one theory has been yet capable to exact prediction of the elementary particle mass-energy, although some interesting attempts have been made [21]. The problem remains far to be solved and this is why any step forward is of great interest.
Regarding the results of prediction of the vibrational energy levels for hydrogen molecule, the best regression equation obtained for the first twelve levels was
 (8)
(8)
N =12 R =0.9998 SE = 2.6275 F = 26602.74 The symbols in Equation (8) are Ev = Vibrational energy (KJ/mole).
ESpm03r = Spectral moment 03 from edge adjacency matrix weighted by resonance integrals.
N = Number of data.
R = Regression coefficient.
SE = Standard error of estimate.
F = Fischer-Snedecor parameter.

Table 3. Allocation of graphs and comparison between observed and calculated values of vibrational energies for the molecule of hydrogen.
Table 3 illustrates the comparison between the experimental values and those calculated from the Equation (8). As can be observed, in this case the graph G2 is assigned to the first quantum state (v = 0), because of the existence of the vibrational residual energy in the anharmonic oscillator.
As seen, another spectral moment, namely ESpm03r, accounts for more than 99% of the variance, what is important because we are in presence of a completely different physical system.
The preponderant role of spectral moments as a measure of the energy in different systems has enough precedents in the literature, although little application has been done so far on particle physics. For example, Broote and Körner have posed arguments on the role of spectral moments in perturbation theory, particularly in the study to the low-energy hadron production associated to electron-positron annihilation [22].
The spectral moments have been related elsewhere to the concept of “energy of graphs” [23]. Moreover, Estrada [24] has demonstrated in a very solid way that the spectral moments can be related to the energy of any system, according to the equation:
 (9)
(9)
where E(t) are the different types of energies involved and ε(t) are the discrete values of the energy levels for energy of type t.  is the spectral density function and
is the spectral density function and 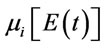 are the corresponding spectral moments associated to that type of energy.
are the corresponding spectral moments associated to that type of energy.
Based on Equation (9), for a given spectral moment
value, for example , and given that the spectral density function is continuous and differentiable, the energy of the system can be expressed as a series expansion by powers of
, and given that the spectral density function is continuous and differentiable, the energy of the system can be expressed as a series expansion by powers of  in the form:
in the form:
 (10)
(10)
where c and c' are just two proportionality constants. Taking logarithms and considering that in our case we have a vibrational energy,  , it results:
, it results:
 (11)
(11)
Since the vibrational energy is the mass of the particle (in GeV units), 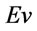 may be replaced by m (mass of the particle), so coming finally to the equation:
may be replaced by m (mass of the particle), so coming finally to the equation:
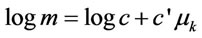 (12)
(12)
Equation (12) stands for a possible theoretical interpretation of Equations (5) and (6), however the definitive interpretation of the role of the topological indices in Equations (5), (6) and (8) remains an open question that might perhaps encourage other fellow experts to take over the issue under the framework of theoretical physics.
The application of graphs in various fields, particularly in molecules, has been extremely productive, demonstrating to be a very effective tool for predicting molecular properties [25-27].
Furthermore, our research group has cover a long way in the topological design of new drugs [28-30].
Not surprisingly, the topology associated to graphs can also be useful in predicting properties in other areas, such as that of atomic and subatomic systems. As previously mentioned, the role of graphs in the interactions between particles (Feynman diagrams) and in string theory, is well known. However, it is noteworthy that the contribution done here is significant because it shows how the graph-theoretical algorithms can perform simple calculation of atomic and sub-atomic properties, what in turn might suggest new approaches to solve the much more complex problems associated with the theoretical formalisms of particle physics.
4. Conclusion
The use of graph-theoretical indices for the prediction of properties of atomic and subatomic particles is a rather unexplored field. The results outlined here demonstrate that this approach can be useful on this goal. Indeed, although there must be other alternative graph-theoretical algorithms as the one illustrated here, it seems clear that it points toward a new framework that can yield interesting results in the near future.
5. Acknowledgements
The author thanks the Spanish Ministry of Science and Innovation by its Grant project SAF2009-13059-C03-02. He is also grateful to Maria Galvez-Llompart for her invaluable help in preparing this work.
REFERENCES
- Smolin and J. Harnad, “The Trouble with Physics: The Rise of String Theory, the Fall of a Science, and What Comes Next,” The Mathematical Intelligencer, Vol. 30, No. 3, 2008, pp. 66-69. doi:10.1007/BF02985383
- R. P. Feynman, “The Theory of Positrons,” Physical Review, Vol. 76, No. 6, 1949, pp. 749-759. doi:10.1103/PhysRev.76.749
- F. Harary, “Proof Techniques in Graph Theory,” Academic Press Inc., Burlington, 1969.
- M. C. Heydemann and B. Ducourthial, “Cayley Graphs and Interconnection Networks,” Physics, Science & Math, Vol. 497, No. 497, 1997, pp. 167-226.
- J. J. Sylvester and F. Franklin, “A Constructive Theory of Partitions, Arranged in Three Acts, an Interact and an Exodion,” American Journal of Mathematics, Vol. 5, No. 1, 1882, pp. 251-330. doi:10.2307/2369545
- T. M. Cover, “Comments on Broadcast Channels,” IEEE Transactions on Information Theory, Vol. 44, No. 6, 1998, pp. 2524-2530. doi:10.1109/18.720547
- N. Deo, “Graph Theory with Applications to Engineering and Computer Science,” PHI Learning Ltd., New Delhi, 2004.
- W. Ren, “Synchronization of Coupled Harmonic Oscillators with Local Interaction,” Automatica, Vol. 44, No. 12, 2008, pp. 3195-3200. doi:10.1016/j.automatica.2008.05.027
- A. W. Wolfe, “Social Network Analysis: Methods and Applications,” American Ethnologist, Vol. 24, No. 1, 1997, pp. 219-220. doi:10.1525/ae.1997.24.1.219
- F. Harary, “Graph Theory and Theoretical Physics,” Academic Press, New York, 1967.
- T. M. J. Fruchterman and E. M. Reingold, “Graph Drawing by Force-Directed Placement,” Software: Practice and Experience, Vol. 21, No. 11, 1991, pp. 1129-1164. doi:10.1002/spe.4380211102
- N. Cabibbo, “Unitary Symmetry and Leptonic Decays,” Physical Review Letters, Vol. 10, No. 12, 1963, pp. 531- 533. doi:10.1103/PhysRevLett.10.531
- B. Greene, “The Elegant Universe,” Vintage Books, New York, 2000.
- R. Penrose, “Applications of Negative Dimensional Tensors,” Academic Press Inc., Burlington, 1971.
- J. Galvez, R. Garcia-Domenech and J. V. de Julian-Ortiz, “Assigning Wave Functions to Graphs: A Way to Introduce Novel Topological Indices,” Communications in Mathematical and in Computer Chemistry, Vol. 56, No. 3, 2006, pp. 509-518.
- I. Levine, “Quantum Chemistry,” 5th Edition, Prentice Hall, New Jersey ,1999.
- T. Filk, “Relational Interpretation of the Wave Function and a Possible Way Around Bell’s Theorem,” International Journal of Theoretical Physics, Vol. 45, No. 6, 2006, pp. 1166-1180. doi:10.1007/s10773-006-9125-0
- Dragon, “Talete Srl,” Milano, 2006. http://www.talete.mi.it/
- W. J. Dixon, M. B. Brown, L. Engelman and R. I. Jennrich, “7M Package,” University of California Press, San Francisco, 1990.
- E. Estrada, “Spectral Moments of the Edge Adjacency Matrix of Molecular Graphs. 1. Definition and Applications to the Prediction of Physical Properties of Alkanes,” Journal of Chemical Information and Computer Sciences, Vol. 36, No. 4, 1996, pp. 844-849. doi:10.1021/ci950187r
- G. N. Shah and T. A. Mir, “Are Elementary Particle Masses Related,” The 29th International Cosmic Ray Conference, Pune, 3-10 August 2005, pp. 219-222.
- S. Groote and J. G. Körner, “Spectral Moments of TwoPoint Correlators in Perturbation Theory and Beyond,” Physical Review, Vol. 65, No. 3, 2002, 30 p. doi:10.1103/PhysRevD.65.036001
- B. Zhou, I. Gutman, J. A. de la Peña, J. Rada and L. Mendoza, “On Spectral Moments and Energy of Graphs,” Communications in Mathematical and in Computer Chemistry, Vol. 57, No. 1, 2007, pp. 183-191.
- E. Estrada, “Quantum-Chemical Foundations of the Topological Substructure Molecular Design,” The Journal of Physical Chemistry, Vol. 112, No. 23, 2008, pp. 5208-5217. doi:10.1021/jp8010712
- L. B. Kier, W. J. Murray, M. Randić and L. H. Hall, “Molecular Connectivity V: Connectivity Series Concept Applied to Density,” Journal of Pharmaceutical Sciences, Vol. 65, No. 8, 1976, pp. 1226-1230. doi:10.1002/jps.2600650824
- R. Garcia-Domenech, J. Galvez, J. V. de Julian-Ortiz and L. Pogliani, “Some New Trends in Chemical Graph Theory,” Chemical Reviews, Vol. 108, No. 3, 2008, pp. 1127-1169. doi:10.1021/cr0780006
- S. C. Basak, D. R. Mills, A. T. Balaban and B. D. Gute, “Prediction of Mutagenicity of Aromatic and Heteroaromatic Amines from Structure: A Hierarchical QSAR Approach,” Journal of Chemical Information and Computer Sciences, Vol. 41, No. 3, 2001, pp. 671-678. doi:10.1021/ci000126f
- P. Jasinski, B. Welsh, J. Galvez, D. Land, P. Zwolak, et al., “A Novel Quinoline, MT477: Suppresses Cell Signaling through Ras Molecular Pathway, Inhibits PKC Activity, and Demonstrates in vivo Anti-Tumor Activity against Human Carcinoma Cell Lines,” Investigational New Drugs, Vol. 26, No. 3, 2008, pp. 223-232. doi:10.1007/s10637-007-9096-x
- P. Jasinski, P. Zwolak, R. Isaksson, V. Bodempudi, K. Terai, et al., “MT103 Inhibits Tumor Growth with Minimal Toxicity in Murine Model of Lung Carcinoma via Induction of Apoptosis,” Investigational New Drugs, Vol. 29, No. 5, 2011, pp. 846-852. doi:10.1007/s10637-010-9432-4
- J. Galvez, J. Llompart, D. Land and G. M. Pasinetti, “Compositions for Treatment of Alzheimer’s Disease Using Abeta-Reducing and/or Abeta-Anti-Aggregation Compounds,” US Patent No. 2010114636, 2010.

