Int. J. Communications, Network and System Sciences, 2010, 3, 779-787
doi:10.4236/ijcns.2010.310104 Published Online October 2010 (http://www.SciRP.org/journal/ijcns)
A Comparative Analysis of Tools for Verification of
Security Protocols
Nitish Dalal, Jenny Shah, Khushboo Hisaria, Devesh Jinwala
Department of C om put er Engineerin g,
S.V. National Institute of Technology, Ichchhanath, Surat, India
Received July 20, 201 0; revised August 21, 2010; accepted September 24, 2010
Abstract
The area of formal verification of protocols has gained substantial importance in the recent years. The re-
search results and subsequent applications have amply demonstrated that the formal verification tools have
indeed helped correct the protocols even after being standardized. However, the standard protocol verifica-
tion tools and techniques do not verify the security properties of a cryptographic protocol. This has resulted
in the emergence of the security protocol verifiers to fill the need. In this paper, taking the two popular secu-
rity verification tools namely Scyther and ProVerif as the basis, we identify a few security protocols and im-
plement them in both Scyther and ProVerif, to aptly evaluate the tools, in terms of the security properties of
the selected protocols. In the process, we not only characteristically present a comparative evaluation of the
two tools, but also reveal interesting security properties of the protocols selected, showing their strengths and
weaknesses. To the best of our knowledge, this is a unique attempt to juxtapose and evaluate the two verifi-
cation tools using the selected security protocols.
Keywords: Formal Verification, Security Protocols, Attacks
1. Introduction
A protocol is a set of rules that followed the defined
conventions to establish semantically correct communi-
cations between the participating entities. A security
protocol is an ordinary communication protocol in which
the message exchanged is often encrypted using the de-
fined cryptographic mechanisms. The mechanisms Sym-
metric Key Cryptography or Asymmetric Key Cryptog-
raphy are used to obtain various cryptographic attributes
such as Confidentiality, Entity Authentication, Message
Integrity, Non-repudiation, Message Freshness, to name
a few [1]. However, merely using cryptographic mecha-
nisms, does not guarantee security-wise semantically
secure operation of the protocol, even if it is correct.
There indeed have been reported breaches in the security
protocols, after being published and accepted as a safe
protocol [2-4]. In such a scenario, in case of the ordinary
communication protocols, recourse has been taken to the
rigorous verification of the same using appropriate tool
for the domain. As for example, the protocol verifier
SPIN is used to verify the communication protocols for
distributed software [5].
Such successful use of the formal methods for veri-
fication has led to the upsurge in devising similar tools
for verifying the security properties of a cryptographic
protocol, too. In order to gain confidence in the crypto-
graphic protocol employed, it has been found desirable
that the protocol be subjected to an exhaustive analysis
that verifies its security properties. Some of the tools
developed for the purpose are Scyther [6], ProVerif [7],
Athena [8], Avispa [9], Casper/FDR to name a few. Thes e
tools differ in their input language and also in the way
they verify the protocols and provide the output.
However, an important fall-out of the emergence of a
plethora of such tools is that, it often becomes difficult
for a security engineer to identify the appropriateness
and suitability of a tool for the protocol under considera-
tion. Motivated with this difficulty, we in this research
report, document our attempt at evaluating the two
popular cryptographic verification tools namely ProVerif
and Scyther. We use six popular cryptographic protocols
to implement the same and then analyze the protocols,
using both these tools. In the process, interestingly, we
not only comparatively evaluate the tools under consid-

N. DALAL ET AL.
780
eration, but also iden tify various interesting properties of
the protocols used.
To the best of our knowledg e, this is a unique attempt
to juxtapose and evaluate the two verification tools using
the security protocols namely the Kao Chow Authentica-
tion Protocol [10], the 3-D Secure Protocol [11], the
Needham Schroeder Public Key Protocol [3], the An-
drew Secure RPC Protocol [12], the Challenge Hand-
shake Authentication Protocol [13] and the Diffie-
Hellman Key Exchange Protocol [14].
The rest of this paper is organized as follows: in sec-
tion 2, we describe the theoretical background which
includes a brief introduction of Scyther and ProVerif
tools. In section 3, we formally define the problem and
survey the related work. In section 4, we present details
of our implementation of various protocols, whereas do a
comparative analysis of the two tools, before we draw
the conclusion and show probab le futur e work, in the last
section.
2. Theoretical Background
2.1. Cryptographic Verification Tools
As mentioned before, one can find a series of tools for
the verification of the cryptographic protocols. We have
selected Scyther and ProVerif amongst all these, for the
comparative evaluation. This decision is largely driven
by the popularity of these two tools amongst all, we sur-
veyed. In this section we depict the vital characteristics
of these two tools.
2.1.1. Scyther
Scyther is a tool used for security protocol verification,
where it is assumed that all the cryptographic functions
are perfect. The tool provides a graphical user interface
that makes it easier to verify and understand a protocol.
In addition, attack graphs are generated whenever an
attack is found corresponding to the claim mentioned.
The tool can also verify all the possible claims on the
protocol. The tool can be used to find problems that arise
from the way the protocol is constructed. It can also be
used to generate all the possible trace patterns. The veri-
fication here can be done using a bounded or an un-
bounded number of sessions. The language used to write
protocols in Scyther is SPDL (Security Protocol Descrip-
tion Language) [6].
2.1.2. ProVerif
ProVerif is a software tool for automated reasoning
ab ou t th e se cu rity properties found in cryptographic proto-
cols. This was developed by Bruno Blanchet. This tool
verifies the protocol for an unbounded number of ses-
sions, using unbounded message space. The tool is capa-
ble of attack reconstruction—wherein if a property cannot
be proved, an execution trace which falsifies the desired
property is constructed. There are two ways of providing
input to this tool—Horn clauses or Pi calculus. In both
cases, the output of the tool is essentially the same. Ex-
plicit modeling of attacker is not required. It is also pos-
sible to state whether an attacker is active or passive [7].
3. Related Work
The main objective of our research is to dissect the
two protocol verification tools, Scyther and ProVerif,
and to provide a comparative analysis of the two. In
order to analyze the tools, suitable standard input pro-
tocols are required to be identified. After careful ob-
servation of a series of such protocols, we have identi-
fied, implemented and analyzed six different security
protocols using both these tools. As mentioned earlier,
these protocols are namely the Kao Chow Authentica-
tion Protocol, the 3-D Secure Protocol, the Needham
Schroeder Public Key Protocol, the Andrew Secure
RPC Protocol, the Challenge Handshake Authentica-
tion Protocol and the Diffie Hellman Key Exchange
Protocol.
One can find a few attempts in the literature that con-
centrate on tools used for protocol verification, whereas
very few of them provide a comparative analysis of pro-
tocol verification tools as in [15] and in [16]. However,
there is no attempt that either focuses on or subsumes a
detailed comparative analysis of the tools Scyther and
Proverif, using the actual implementation of protocols as
the basis. Hence, we believe our attempt here to be a
unique one of its kind.
In the next section, we discuss briefly the implementa-
tion of each of the protocol in Scyther as well as in
ProVerif and analyze the same.
4. Implementation and Analysis
4.1. Kao Chow Authentication Protocol
4.1.1. Defi n i ti on
The Kao Chow protocol is a mutual authentication and
key distribution protocol aiming at strong authentication
and low message overhead. A trusted third party, S, is
used to generate and distribute keys. It is the responsibil-
ity of S to generate a fresh secret session key k. The two
communicating parties, A and B, will use this key to
encrypt future message exchanges. Both the parties have

N. DALAL ET AL.
781
secret keys shared with the server, Kas and Kbs, which
are used to encrypt and decrypt any messages that are
exchanged. Further, the protocol aims to authenticate the
parties A and B to each other using their nonces Na and
Nb [10]. The pseudocode of a typical protocol execution
run is shown in Figure 1.
Kao_Chow(Kas, Kbs)
/* nonce = random number,
id_X = identity of X,
A,B = the communicating parties,
S = Server,
Kas = symmetric key between A and S,
Kbs = symmetric key between B and S,
k = session key between A and B */
{
Call (Sender_A(Kas) | Receiver_B(Kbs) |
Server_S(Kas,Kbs)).
/* Call the functions in parallel */
}
Sender_A(Kas)
{
StepA1:generate nonce Na;
msg1 = (id_A,id_B,Na);
send msg1 to S;
call StepS1.
StepA2:receive msg3 from B;
let msg3 = (part1, part2, Nb’);
let (id_A’’,id_B’’,Na’’,k)
=(sym_decrypt(part1) with Kas) AND
check_if(id_A’’= id_ A) AND chec k_if(i d_ B’’= id_B)
AND check_if(Na’’ = Na);
let (Na’’’) = (sym_decrypt(part2) with k) AND
check_if(Na’’’ = Na);
msg4 = sym_encrypt(Nb’) with k;
send msg4 to B;
call StepB2.
}
Server_S(Kas, Kbs)
{
StepS1:receive msg1 from A;
let (id_A',id_B',Na’) = msg1;
generate session_key k;
msg2 = ((sym_encrypt
(id_A',id_B',Na’,k)
with Kas),
(sym_encrypt(A',B',Na’,k)
with Kbs));
send msg2 to B;
call StepB1.
}
Receiver_B(Kbs)
{
StepB1:receive msg2 from S;
let(part1,part2) = msg2;
let(id_A’’,id_B’’,Na’’,k)=
sym_decrypt(part2) with Kbs;
generate nonce Nb;
msg3 = (part1,(sym_encrypt (Na’’) with k),Nb);
send msg3 to A;
call StepA2.
StepB2:receive msg4 from A;
let(Nb’’)=(sym_decrypt msg4 with k)
AND check_if(Nb’’ = Nb);
return to Kao_Chow( ).
}
Figure 1. Kao Chow authentication protocol.
4.1.2. Analysis
When this protocol is verified using Scyther, attacks are
found on the sender side as well as on the receiver side.
However, we observe that the session key on the sender
side (A) is secret whereas it is compromised on the re-
ceiver side. Because of this, there are synchronization
and agreement attacks on both the sides. For the claim to
check the secrecy of session key on the receiver (B) side,
scyther outputs saying the claim is “Falsified” and that
there is “At least 1 attack.” When a similar query is writ-
ten for the initiator side, scyther gives the outpu t that the
claim has been “Verified” and that there are “No at-
tacks”.
When the same protocol is analyzed using ProVerif,
we obtain a similar result. That is, it can also detect that
the session key is not secret on the receiver side. The
private free variable var is encrypted using the session
key k and published over a public channel c, the output
obtained is false i.e., the key is not secret on the initiator
side. When a similar query is provided for the receiver
side, ProVerif gives the output saying that session key is
secret on the receiver side. When the parameter “at-
tacker” is set to passive, we do not obtain any attacks
showing that there ar e no passive attacks on the protocol.
The symmetric key Kas is secret on A side as well as the
server(S) side. Kbs is also secret on the server side as
well as B side.
4.2. 3-D Secure Protocol
4.2.1. Defi n i ti on
The 3-D Secure is an XML-based protocol used as an
added layer of security for online credit and debit card
transactions. Developed by Visa, its aim is to improve
the security of Internet payments. It is offered to cus-
tomers as the Verified by Visa service. It has also been
adopted by MasterCard, under the name MasterCard
SecureCode.
A transaction using Verified by Visa/SecureCode will
initiate a redirect to the website of the card issuing bank
to authorize the transaction. Each Issuer could use any
kind of authentication method. The most common ap-
proach is a password-based method. Thus, to effectively
buy on the Internet means using a secret password tied to
the card. The Verified by Visa protocol recommends the
bank’s verification page to load in an inline frame ses-
sion. In this way, the bank’s systems can be held respon-
sible for most security leaks [11].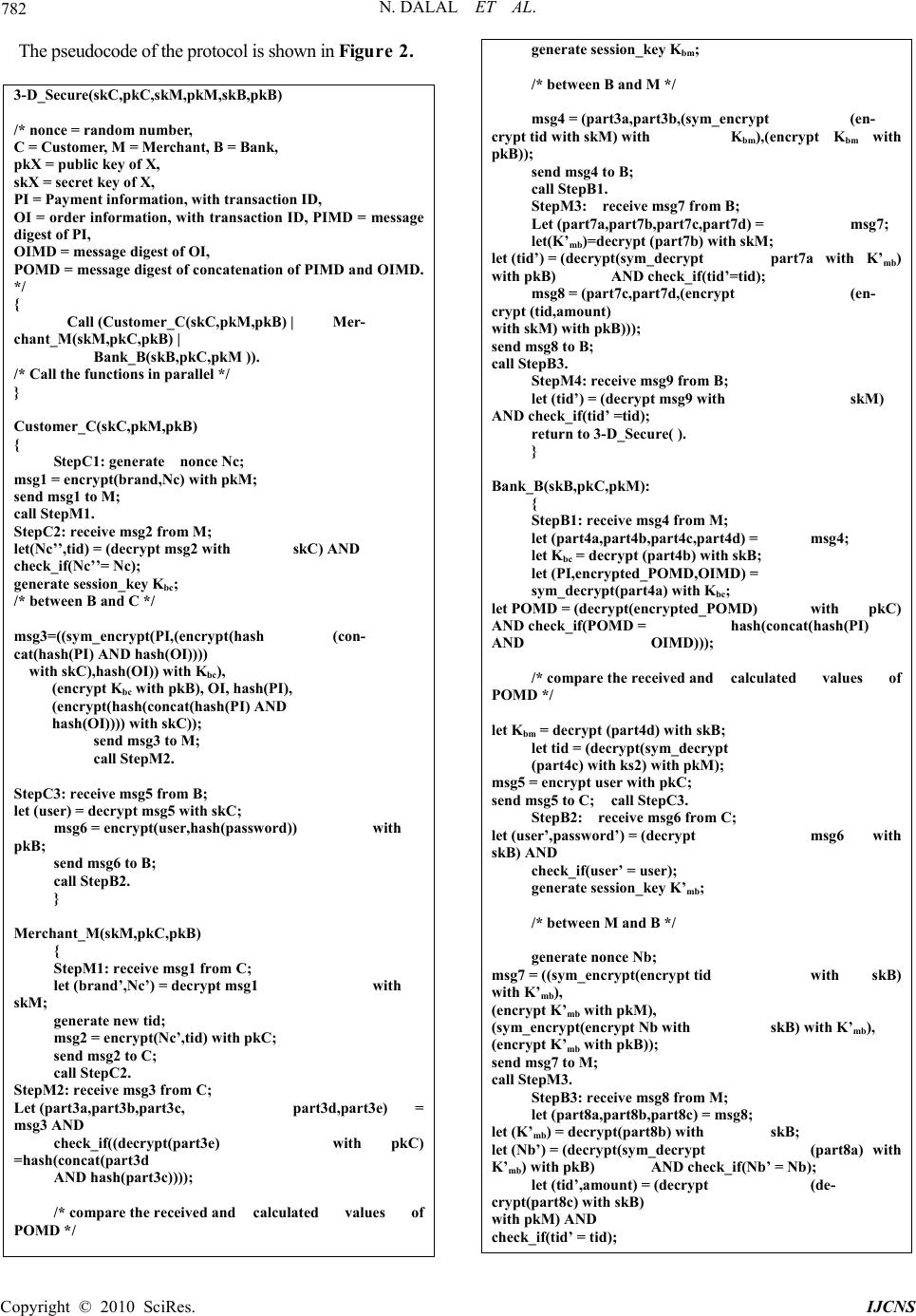

N. DALAL ET AL.
782
The pseudocode of the protocol is shown in Figu re 2.
3-D_Secure(skC,pkC,skM,pkM,skB,pkB)
/* nonce = random number,
C = Customer, M = Merchant, B = Bank,
pkX = public key of X,
skX = secret key of X,
PI = Payment information, with transaction ID,
OI = order information, with transaction ID, PIMD = message
digest of PI,
OIMD = message digest of OI,
POMD = message digest of concatenation of PIMD and OIMD.
*/
{
Call (Customer_C(skC,pkM,pkB) | Mer-
chant_M(skM,pkC,pkB) |
Bank_B(skB,pkC,pkM )).
/* Call the functions in parallel */
}
Customer_C(skC,pkM,pkB)
{
StepC1: generate nonce Nc;
msg1 = encrypt(brand,Nc) with pkM;
send msg1 to M;
call StepM1.
StepC2: receive msg2 from M;
let(Nc’’,tid) = (decrypt msg2 with skC) AND
check_if(Nc’’= Nc);
generate session_key Kbc;
/* between B and C */
msg3=((sym_encrypt(PI,(encrypt(hash (con-
cat(hash(PI) AND hash(OI))))
with skC),hash(OI)) with Kbc),
(encrypt K
bc with pkB), OI, hash(PI),
(encrypt(hash(concat(hash(PI) AND
hash(OI)))) with skC));
send msg3 to M;
call StepM2.
StepC3: receive msg5 from B;
let (user) = decrypt msg5 with skC;
msg6 = encrypt(user,hash(password)) with
pkB;
send msg6 to B;
call StepB2.
}
Merchant_M(skM,pkC,pkB)
{
StepM1: receive msg1 from C;
let (brand’,Nc’) = decrypt msg1 with
skM;
generate new tid;
msg2 = encrypt(Nc’,tid) with pkC;
send msg2 to C;
call StepC2.
StepM2: receive msg3 from C;
Let (part3a,part3b,part3c, part3d,part3e) =
msg3 AND
check_if((decrypt(part3e) with pkC)
=hash(concat(part3d
AND hash(part3c))));
/* compare the received and calculated values of
POMD */
generate session_key Kbm;
/* between B and M */
msg4 = (part3a,part3b,(sym_encrypt (en-
crypt tid with skM) with Kbm),(encrypt Kbm with
pkB));
send msg4 to B;
call StepB1.
StepM3: receive msg7 from B;
Let (part7a,part7b,part7c,part7d) = msg7;
let(K’mb)=decrypt (part7b) with skM;
let (tid’) = (decrypt(sym_decrypt part7a with K’mb)
with pkB) AND check_if(tid’=tid);
msg8 = (part7c,part7d,(encrypt (en-
crypt (tid,amount)
with skM) with pkB)));
send msg8 to B;
call StepB3.
StepM4: receive msg9 from B;
let (tid’) = (decrypt msg9 with skM)
AND check_if(tid’ =tid);
return to 3-D_Secure( ).
}
Bank_B(skB,pkC,pkM):
{
StepB1: receive msg4 from M;
let (part4a,part4b,part4c,part4d) = msg4;
let Kbc = decrypt (part4b) with skB;
let (PI,encrypted_POMD,OIMD) =
sym_decrypt(part4a) with Kbc;
let POMD = (decrypt(encrypted_POMD) with pkC)
AND check_if(POMD = hash(concat(hash(PI)
AND OIMD)));
/* compare the received and calculated values of
POMD */
let Kbm = decrypt (part4d) with skB;
let tid = (decrypt(sym_decrypt
(part4c) with ks2) with pkM);
msg5 = encrypt user with pkC;
send msg5 to C; call StepC3.
StepB2: receive msg6 from C;
let (user’,password’) = (decrypt msg6 with
skB) AND
check_if(user’ = user);
generate session_key K’mb;
/* between M and B */
generate nonce Nb;
msg7 = ((sym_encrypt(encrypt tid with skB)
with K’mb),
(encrypt K’mb with pkM),
(sym_encrypt(encrypt Nb with skB) with K’mb ),
(encrypt K’mb with pkB));
send msg7 to M;
call StepM3.
StepB3: receive msg8 from M;
let (part8a,part8b,part8c) = msg8;
let (K’mb) = decrypt(part8b) with skB;
let (Nb’) = (decrypt(sym_decrypt (part8a) with
K’mb) with pkB) AND check_if(Nb’ = Nb);
let (tid’,amount) = (decrypt (de-
crypt(part8c) with skB)
with pkM) AND
check_if(tid’ = tid);

N. DALAL ET AL.
783
msg9 = encrypt tid with pkM;
send msg9 to M;
call StepM4.
}
Figure 2. 3-D secure protocol.
4.2.2. Analysis
On analyzing this protocol with Scyther, we find that for
five runs of the protocol, there are no attacks on the cus-
tomer(C) and merchant(M) side. However, the attacks
are found on the bank(B) side. The session key Kbc and
the customer’s password are secret on C side. On the M
side, we find that the session keys Kbm, K’mb and Kbc are
secret. On analyzing the claims on B side, we find that
the session key K’mb and the customer’s password are
secret. But, the keys Kbc and Kbm can be compromised
here. These attacks bring a limitation of the tool Scyther
to the fore. In Scyther, we have no provision of compar-
ing the values of two variables. For instance, in step 4,
the bank receives POMD, PI and hash (OI). However,
there is no way that we can write an “if” condition in this
tool to check the equality of the received POMD and the
calculated POMD (calculated using the function “hash”
and the received value of hash(OI) and PI). The attacks
that we see here are the result of such deficiencies in the
tool. Had there been a way to compare values here, no
attacks would have been found. In order to obtain attacks
on session keys, a special “key-compromise” part needs
to be added to the protocol. In this module, we first spec-
ify who the communicating parties are. Next, we provide
the intruder with all the packets that have been used in a
session and the values of the session keys for that session
in order to verify if a freshness attack is possible.
When the 3D-secure protocol is analyzed using Pro-
Verif, no attacks are found. That is, the too l says that this
protocol is perfectly secure and that there is no way that
an intruder can g ain know ledge of eith er th e session ke ys
(Kbc, Kbm, K’mb) or the customer’s password. This is be-
cause, in this tool we have the provision of writing an
“if” condition to check for the equ ality of two values. For
instance, in step B1, we see that the value POMD ob-
tained after decrypting a part of the message can be
compared to the calculated value of POMD (using the
received values PI and OIMD and the hash function) and
the protocol proceeds only if these two values are found
to be the same. This way, all the attacks are countered
and the protocol becomes completely secure.
Thus, we see that ProVerif provides this advantage
over Scyther. Not being able to compare values in
Scyther leads to attacks being found whereas in ProVerif,
as the values can be compared, these attacks are not
found.
4.3. Needham-Schroeder Public Key Protocol
4.3.1. Defi n i ti on
The Needham-Schroeder Public Key Protocol, based on
public-key cryptography, is intended to provide mutual
authentication between two parties communicating on a
network. It is assumed here that the two parties know the
public key of the oth er. Thus, encrypting the data is pos-
sible using the public key of the other party. Here, A and
B represent the communicating parties [3].
The pseudoco de of the protocol is sh own in Figure 3.
4.3.2. Analysis
On verifying this protocol using Scyther, attacks are
found. It is seen that all the attacks are on the B (receiver)
side. Both the nonces, Na and Nb, can be obtained by the
attacker. In addition, there are synchronization and agree-
ment attacks. Thus, the protocol is not secu re. In addition,
Scyther provides the facility of observing all possible
trace patterns. For this protocol, a single trace pattern is
obtained on the A (initiator) side as there is no intrusion
possible here .
Needham_Schroeder(skA,pkA,skB,pkB)
/* pkX = public key of X,
skX = secret key of X,
nonce = random number,
id_X = identity of X,
A,B = the communicating parties. */
{
Call (Sender_A(skA,pkB) | Receiver_B(skB,pkA)).
/* Call the functions in parallel */
}
Sender_A(skA, pkB)
{
StepA1: generate nonce Na;
msg1 =(encrypt(Na, id_A) with pkB);
send msg1 to B;
call StepB1.
StepA2: receive msg2 from B;
let(Na',Nb',X)=(decrypt(msg2) with sk A) AND
check_if(Na' = Na) AND check_if(X = B);
/* assign the 3 parameters of msg2 on decryption to
Na’,Nb’,X respectively */
msg3 = (encrypt(Nb') with pkB);
send msg3 to B;
call StepB2.
}
Receiver_B(skB,pkA)
{
Step B1: receive(msg1) from A;
let(Na',A')=(decrypt(msg1)with skB);
generate nonce Nb;
msg2 = (encrypt(Nz,Nb,B) with pkA);
send(msg2) to A;
call StepA2.

N. DALAL ET AL.
784
Step B2: receive(msg3) from A;
let (Nb') = (decrypt(msg3) with skB)
AND check_if(Nb' = Nb);
return to Needham_Schroeder().
}
Figure 3. Needham schr oe de r public key protocol.
On B side, 2 trace patterns are obtained—one showing
the normal run of the protocol and the other showing the
man-in-the-middle attack. No attacks are found when the
protocol is verified for a single run. But with 2 or greater
runs, attacks are generated.
In ProVerif, the protocol is run for an unbounded
number of times. For checking the secrecy of nonces and
keys in ProVerif, a random number is generated and it is
encrypted using the nonce and broadcasted over a public
channel. The results obtained are similar to those ob-
tained using Scyther. But, there is no way of checking
for the synchronization and agreement attacks on either
the receiver or the sender side.
4.4. Andrew Secure RPC Protocol
4.4.1. Defi n i ti on
This protocol is intended to distribute a new session key
between two parties A and B. The protocol must guaran-
tee the secrecy of the new shared key k. In every session,
the value of k must be known only by the participants
playing the roles of A and B. The protocol must guaran-
tee the authenticity of k. In every session, on reception of
message 4, A must be able to ensure that the key k in the
message has been created by A in the same session. The
final message contains N'b which can be used in future
messages as a handshake number [12].
The pseudoco de of the protocol is sh own in Figure 4.
Andrew_Secure_RPC(Kab)
/* nonce = random number,
id_X = identity of X,
A,B = the communicating parties,
Kab = symmetric key between A and B,
k = session key between A and B. */
{
Call (Sender_A(Kab) | Receiver_B(Kab)).
/* Call the functions in parallel */
}
Sender_A(Kab)
{
StepA1: generate nonce Na;
msg1 = (id_A, (sym_encrypt(Na) with Kab));
send msg1 to B;
call StepB1.
StepA2: receive msg2 from B;
let (Na'',Nb')=(sym_decrypt msg2 with Kab) AND
check_if(Na'' = Na+1);
msg3 = sym_encrypt(Ns'+1) with Kab;
send msg3 to B;
call StepB2.
StepA3: receive msg4 from A;
let (k,Nb1') = sym_decrypt(msg4) with
Kab;
return to Andrew_Secure_RPC( ). }
Receiver_B(Kab)
{
StepB1: receive msg1 from A;
let (id_A’,part) = msg1;
let (Na') = sym_decrypt(part) with Kab;
generate nonce Nb;
msg2 = sym_encrypt (Na'+1,Nb) with Kab;
send msg2 to A;
call StepA2.
StepB2: receive msg3 from A;
let (Nb'') = (sym_decrypt msg3 with Kab)
AND
check_if(Nb'' = Nb+1);
generate nonce Nb1;
generate session_key k;
msg4 = sym_encrypt(k,Nb1) with Kab;
send msg4;
call StepA3.
}
Figure 4. Andrew secure RPC protocol.
4.4.2. Analysis
When this protocol is verified using Scyther, attacks are
found on the initiator side and none are obtained on the
receiver side. The major attack is the one in which the
session key is compromised. This is a freshness attack on
the protocol. In this, an intruder can replay an old mes-
sage (the last message) and the party A has no way of
knowing that this has come from B or some intruder.
Thus, the intruder can establish a session with A using an
older session key. Since the communication is not taking
place in the proper order, there are attacks of synchroni-
zation and agreement as well. For the claim to check the
secrecy of session key k on the initiato r (A) side, scyther
outputs saying the claim is “Falsified” and that there is
“Exactly 1 attack”. The attack graph provides a complete
flow diagram of the actions of the parties and the in-
truder.
ProVerif also prov ides us with a si milar result. That is,
it can also detect that the session key is no t secret on the
initiator side. The private free variable var is encrypted
using the session key k and published over a public
channel c, the output obtained is false i.e. the key is not
secret on the initiator side. When a similar query is pro-
vided for the receiver side, ProVerif gives the output
saying that session key is secret on the receiver side. In
order to obtain a complete trace pattern, the parameter

N. DALAL ET AL.
785
“traceDisplay” can be set to “long”. This provides an
entire description of how the attack is executed. In addi-
tion, when the parameter “attacker” is set to “passive”,
we do not obtain any attacks showing that there are no
passive attacks on the protocol. It can be verified that the
symmetric key Kab is secret on both the sides.
4.5. Challenge Handshake Authentication
Protocol
4.5.1. Defi n i ti on
The Challenge Handshake Authentication Protocol (CHAP)
uses a 3-way handshake to periodically verify the iden-
tity of the party. This is done upon initial link estab-
lishment, and may be repeated anytime after the link
has been established. Once the link is established, the
authenticator sends a challenge message to the party.
The party responds with a value calculated using a
one-way hash function. The authenticator checks the
response against its own calculation of the expected hash
value. If the values match, the authentication is ac-
knowledged; otherwise the connection has to be termi-
nated [13].
The pseudoco de of the protocol is sh own in Figure 5.
Challenge_Handshake(Kas)
/* challenge = a random value sent by server at irregular in-
tervals,
id = identifier,
A = client,
S = server,
Kas = shared secret between S and A. */
{
Call (Server_S(Kas) | Clent_A(Kas)).
/* Call the functions in parallel */
}
Server_S(Kas)
{
StepS1: generate challenge Ns;
msg1 = (Ns, id);
send msg1 to A;
call StepA1.
StepS2: receive msg2 from A;
check_if(hash(concat(Ns AND id AND
Kas)) = msg2);
msg3 = sym_encrypt( id) with Kas;
send msg3 to A;
call StepA2.
}
Client_A(Kas)
{
StepA1: receive msg1 from S;
let (N’s, id’) = msg1;
msg2 = hash (concat(N’s AND id’ AND Kas));
send msg2 to S;
call StepS2.
StepA2: receive msg3 from S;
let (id’’) = (sym_decrypt msg3 with Kas) AND
check_if(id’’= id’).
}
Figure 5. Challenge handsha ke authentication protocol.
4.5.2. Analysis
On analyzing this protocol with scyther, we see that the
symmetric key (shared secret) is secret on both the sides,
the server as well as the party which ne eds to be authen-
ticated. But, there are synchronization and agreement
attacks on A side but not on the server(S) side. These
attacks are caused because the first message from the
server is not encrypted. Thus, it can be captured by any
intruder. But this does not lead to the shared secret be ing
compromised as the message from the A party to the
server is hashed using a one way hush function. Thus,
even if the intru der kno ws th e ha sh v alue and the ha shing
algorithm, there is no way to unhash the v alue and obtain
the original message. A single trace pattern is obtained
for the server side. For the A side, 2 patterns are obtained
—one specifying the normal run of the protocol and the
other giving details of how the communication can be
disrupted.
When this protocol is verified using ProVerif, the
output obtained shows that the symmetric key Kas can-
not be compromised on either the client side or the server
side. Thus, the communication is secure. In addition,
when the parameter “attacker” is set to “passive”, no
attacks are found suggesting that there are no passive
attacks on this protocol.
4.6. Diffie-Hellman Key Exchange Protocol
4.6.1. Defi n i ti on
Diffie–Hellman key exchange (D–H) is a cryptographic
protocol that allows two parties that have no prior
knowledge of each other to jointly establish a shared
secret key over an insecure communications channel.
This key can then be used to encrypt subsequent com-
munications using a symmetric key cipher. There are two
publicly known numbers—a prime number p and a
primitive root of that prime, g. Each party then chooses a
random number which is less than p and using modular
arithmetic, the key is calculated. Thus, a key is ex-
changed between two or more parties over an insecure
channel [14].
The pseudoco de of the protocol is sh own in Figure 6.
Diffie_Hellman( )
/* nonce = random number,
A,B = the communicating parties,
p = a large prime number,
g = a primitive root of p. */

N. DALAL ET AL.
786
{
Call (Sender_A( ) | Receiver_B( )).
/*Call the functions in parallel */
}
Sender_A( )
{
StepA1: select n0;
/* 1 <= n0 < (p-1) */
msg1 = (g^n0 mod p);
send msg1 to B;
call StepB1.
StepA2: receive msg2 from B;
let (part2) = msg2;
Akey = ((part2^n0)mod p);
return to Diffie_Hellman( ).
}
Receiver_B( )
{
StepB1: receive msg1 from A;
let (part1) = msg1;
select n1;
/* 1 <= n1 < (p-1) */
Bkey = ((part1^n1)mod p);
msg2 = (g^n1 mod p);
send msg2 to A;
call StepA2.
}
Figure 6. Diffie Hellman key exchange protocol.
4.6.2. Analysis
When this protocol is verified using ProVerif, we find
that the generated key is not secret on the initiator sid e as
well as the receiver side.
This is because of a man in the middle attack. An int-
ruder is able to capture the public values from both the
legitimate parties and send its own generated public
value to both of them. Thus, an intruder is able to estab-
lish a session key with both the parties.
The Diffie Hellman key exchange cannot be modeled
using Scyther. The reason is that there is no way to show
Table 1. Scyther and Pr oVer if characteristic comparison.
Characteristics of SCYTHER Characteristics of PROVERIF
 The protocol is modeled using the “spdl” language.
 It is possible to run the protocol for either bounded or
unbounded number of sessions.
 Tool comes with its own graphical user interface.
 It generates the following possible outputs namely Prop-
erty holds for n runs, Property is false and attack trace is
shown, Property holds for all traces.
 Attack graphs are generated which give a visual flow
graph of a trace and are self explanatory.
 All possible trace patterns are generated depicting proto-
col execution.
 The communicating parties need to be modele d as roles.
 It doesn’t provide any option to check for equality of
different variables.
 Tool by its own discretion checks for secrecy of all possi-
ble variables, no explicit “claims” are necessary.
 The anticipated intruders along with the legitimate com-
municating parties have to be specified as agents.
 In case of protocols which may suffer from a freshness
attack, we have to put a key compromise module in the
code which specifies that a complete session has been
captured and the intruder also knows the session key .
 There is no concept of channels.
 The protocol is modeled using horn clauses or pi calcu-
lus.
 Tool has to be run through command line interface.
 It generates the following possible outputs namely Prop-
erty is true, Property is false and attack trace is generated,
Property cannot be proven when false attack is found,
Tool might not terminate.
 Step by step trace is generated explaining the run and
attack.
 Trace is generated only for the property which is
checked.
 The communicating parties need to be modeled as proc-
esses.
 Equality can be checked by using “if..then” or “let..in”.
 It checks only those attacks for which the “query” has
been specified in the code.
 ProVerif does not require any such speci ficatio n.
 No special code for a freshness attack needs to be given
in ProVerif.
 Channels need to be specified for communication.
 It is possible to run the protocol only for an unbounded
number of sessions.

N. DALAL ET AL.
787
the equivalence of 2 exponential operations. That is, a
rule that states (exp (exp (g,x),y) mod p) and (exp (exp
(g,y),x) mod p) are the same cannot be specified. Thus, it
is not possible to handle such exponentiations which
need equivalence conditions to be explicitly mentioned.
Hence, the tool is not able to know that the keys that
have to be gene rat ed o n both sides are ideally the same.
5. Conclusions and Future Work
Based on the implementation and evaluation as described
above, we summarize the comparative analysis of Scyt-
her and ProVerif in the Table-I.
From this, it can be observed that applying formal
methods to verify security protocols is an interesting and
challenging research area. Using the tools Scyther and
ProVerif, it is possible to model many security protocols
in standard format, verify them and know the attacks
they are susceptible to. We modeled six characteristic
protocols and verified them using these tools. The tools
vary in regards like their input language, manner in
which the output is provided, the way in which traces of
attacks are generated. Moreover, both the tools have a
few limitations. Using these tools, it is easy to know
what flaws these protocols suffer from so that the flaws
can be rectified. Although verification using these tools
does not ensure that the protocols once verified by these
tools are flawless, still they provide a means to know
many of the flaws easily. As a future work in this area,
we plan to extend this comparative evaluation using
other interesting protocols namely to have a better un-
derstanding of the differences in the cap- abilities o f bo th.
Our work can also be extended to model the same pro-
tocols using ot her to ols to have a wider evaluat i on.
6. Acknowledgements
We are grateful to all those anonymous reviewers for
their useful suggestions, to help give the paper the shape,
it is now, in.
7. References
[1] W. Stallings, “Cryptography and Network Security: Prin-
ciples and Practices,” 4th Edition, Pearson Education,
ISBN-10: 0131873164 ISBN-13: 9780131873162, 2006.
[2] D. Denning and G. Sacco, “Timestamps in Key Distribu-
tion Protocols,” Communications of the ACM, Vol. 24,
No. 8, 1981, pp. 533-536.
[3] R. Needham and M. Schroeder, “Using Encryption for
Authentication in Large Networks of Computers,” Com-
munications of the ACMx, Vol.21, No. 12, 1978, pp. 993-
999.
[4] R. Needham and M. Schroeder, “Authentication Revis-
ited,” ACM SIGOPS Operating Systems Review, Vol. 21,
No. 1, 1987, p. 7.
[5] G. J. Holzmann, “Software Model Checking with SPIN,”
Advances in Computers, Vol. 65, 2005, pp. 78-109.
[6] C. J. F. Cremers, “Scyther-Semantics and Verification of
Security Protocols,” Ph.D. Thesis, Eindhoven University
of Technology, 2006.
[7] B. Blanchet, “An Efficient Cryptographic Protocol Verifier
Based on Prolog Rules,” Proceedings of the 14th IEEE
Computer Security Foundations Workshop (CSFW), Cape
Breton, IEEE Computer Society, 2009, pp. 82-96.
[8] D. Song, “Athena: A New Efficient Automatic Checker
for Security Protocol Analysis,” Proceedings of the12th
IEEE Computer Security Foundations Workshop (CSFW),
IEEE Computer Society, 1999, pp. 192-202.
[9] A. Armando et al., “The AVISPA Tool for the Auto-
mated Validation of Internet Security Protocols and Ap-
plications,” Proceedings of Computer Aided Ve r i fication’05
(CAV), Vol. 3576 of Lecture Notes in Computer Science,
Springer, 2005, pp. 281-285.
[10] I. Kao, Lung and R. Chow, “An Efficient and Secure
Authentication Protocol Using Uncertified Keys,” SI-
GOPS Operating Systems Review, Vol. 29, No. 3, 1995,
pp. 14-21.
[11] Verified By Visa 3-D Secure Protocol. [Online] Avail-
able: https://usa. visa.com/pe rsonal/security/vbv/index.html,
last retrieved on 2nd June 2010.
[12] M. Satyanaray anan, “Integrating Security in a Large Dis-
tributed System,” ACM Transactions on Computer Sys-
tems, Vol. 7, No. 3, 1989, pp. 247-280.
[13] W. Simpson, “PPP Challenge Handshake Authentication
Protocol (CHAP),” August 1996 http://www.ietf.org/rfc/
rfc1994.txt, last retrieved on 2nd June 2010.
[14] W. Diffie and M. E. Hellman, “New Directions in Cryp-
tography,” IEEE Transactions on Information Theory,
Vol. 22, No. 6, 1976, pp. 644-654.
[15] C. J. Cremers, P. Lafourcade and P. Nadeau, “Comparing
State Spaces in Automatic Security Protocol Analysis,”
Formal to Practical Security: Papers Issued from the 2005
-2008 French-Japanese Collaboration, Springer-Verlag,
2009, pp. 70-94.
[16] C. J. Cremers, “Unbounded Verification, Falsification,
and Characterization of Security Protocols by Pattern Re-
finement,” CCS’08: Proceedings of the 15th ACM con-
ference on Computer and communications security, ACM
Press, 2008, pp. 119-128.