Modeling and Numerical Simulation of Material Science, 2013, 3, 16-19
Published Online January 2013 (http://www.SciRP.org/journal/mnsms)
Electronic and Optical Properties of Rocksalt CdO: A
first-Principles Density-Functional Theory Study
Gang Yao1,2, Xinyou An1, Hongwen Lei1, Yajun Fu1, Weidong Wu1,2
Science and Technology on Plasma physics Laboratory, Research Center of Laser Fusion, CAEP, P.O.Box 919-983, Mianyang
621900, P.R. China
State Key Laboratory Cultivation Base for Nonmetal Composites and Functional Materials, School of Materials Science and
Engineering, Southwest University of Science and Technology, Mianyang 621010, P.R. China
Received 2012
ABSTRACT
The structural, electronic and optical properties of rocksalt CdO have been studied using the plane-wave -based pseudo-
potential density functional theory within generalized gradient approximation. The calculated lattice parameters are in
agreement with previous experimental work. The band structure, density of states, and Mulliken charge population are
obtained, which indicates that rocksalt CdO having the properties of a halfmetal due to an indirect band gap of -0.51eV.
The mechanical properties show that rocksalt CdO is mechanically stable, isotropic and malleable. Significantly, we
propose a correct value for ε1(0) of about 4.75, which offers theoretical data for the design and application for rocksalt
CdO in optoelectronic materials.
Keywords: Densit y-Functional Theory; Electronic Structure; Optical Properties; Rocksalt CdO
1. Introduction
Recently, electronic structure and optical properties of
transparent conductive oxides (TCOS) such as cadmium
oxide (CdO) are of tremendously increasing interest, in
response to the industrial demand for semiconductor
photoelectric device operating in solar cell, liquid-cr ystal
displays (LCD), gas sensor, electrochromic devices and
ultraviolet semiconductor laser [ 1, 2]. CdO has various
polymorphs such as Pm3m (
1
h
O
), F-43m (
2
d
T
) and
P63mc (
4
6v
C
), and it crystallizes in the rocksalt structure
wit h Fm -3m (
5
h
O
) space group at room temperature.
However, on applying pressure up to 89GPa [3] (90. 6
GPa [4]), rocksalt CdO undergoes a structural phase
transition to CsCl-type with Pm3m (
1
h
O
).
Several experimental as well as quite a few ab initio
theoretical studies involving method of local density ap-
proximation (LDA) [5], Hartree-Fock method [6], full
potential linearized augmented plane wave (FP-LAPW )
[3] and other calculations based on density functional
theory (DFT) have been performed to study the elastic
and electronic properties of the rocksalt CdO over the
past two decades [2,3,5-9]. Schleife et al. have reported
the complex dielectric function and predicted a static
dielectric function ε1(0) of 7.20 [5]. As we all known,
howe ver, the DFT-GGA scheme tends to underestimate
slightly the bonding in the considered group-II oxide
polymorphs [3,5], i.e., the prediction for ε1(0) is not
reliable.
In order to understand the relevant phenomena and
design process of new materials, it is necessary to insight
into the electronic and optical properties of rocksalt CdO
by the theoretical analysis. So we have made a correction
to optical with scissors operator [1 0] on the basic of the
calculated band gap. And many useful results have been
obtained, which offers theoretical data for the design and
application for rocksalt CdO in optoelectronic materials.
2. Computational Details
The ab initio calculations were performed by employing
plane -wave ultrasoft pseudopotential and implemented in
the most recent version of CASTEP code [11]. The ex-
change and correlation function were given by genera-
lized gradient approximation (GGA) with Per-
dew-Burke -Ernze r hof ,a nd Perdew and Wang (PW91)
[12]. The valence-electron configurations for the ele-
ments of rocksalt CdO are Cd 4d105s2 and O 2s22p4. The
cutoff energy of 600eV was employed through-out the
calculation which was tested to be fully converged with
respect to total energy for different volumes. The Bril-
louin-zone sampling mesh parameters for the k-point set
were 6×6×6 [13]. In addition, this set of parameters as-
sures were implemented: the total energy tolerance of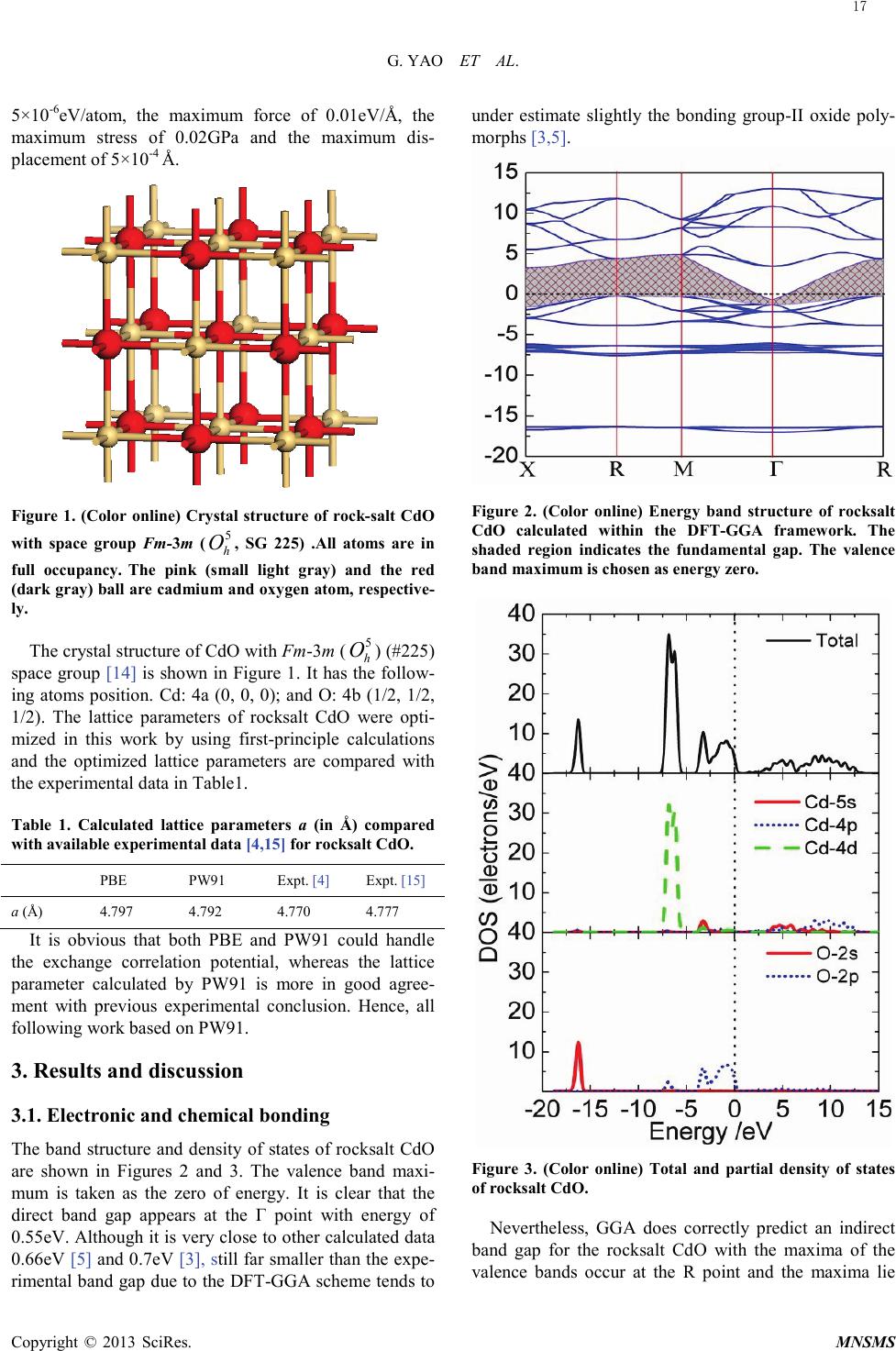

G. YAO ET AL.
5×10-6eV/atom, the maximum force of 0.01eV/Å, the
maximum stress of 0.02GPa and the maximum dis-
placement of 5×10-4 Å.
Figure 1. (Color online) Crystal structure of rock-salt CdO
with space group Fm -3m (
5
h
O
, SG 225) .All atoms are in
full occupancy. The pink (small light gray) and the red
(dark gray) ball are cadmium and oxygen atom, respective-
ly.
The crystal structure of CdO with Fm-3m (
5
h
O
) (#225)
space group [14] is shown in Figure 1. It has the follow-
ing atoms position. Cd: 4a (0, 0, 0); and O: 4b (1/2, 1/2,
1/2). The lattice parameters of rocksalt CdO were opti-
mized in this work by using first-principle calculations
and the optimized lattice parameters are compared with
the experimental data in Table1.
Table 1. Calculated lattice parameters a (in Å) compared
with available experimental data [4,15] for rocksalt CdO.
PBE PW9 1 Expt. [4] Expt. [15]
a (Å) 4.797 4.792 4.770 4.777
It is obvious that both PBE and PW91 could handle
the exchange correlation potential, whereas the lattice
parameter calculated by PW91 is more in good agree-
ment with previous experimental conclusion. Hence, all
following work based on PW91.
3. Results and discussion
3.1. Electronic and chemical bonding
The band structure and density of states of rocksalt CdO
are shown in Fig ures 2 and 3. The valence band maxi-
mum is taken as the zero of energy. It is clear that the
direct band gap appears at the Γ point with energy of
0.55eV. Although it is very close to other calculated data
0.66eV [5] and 0.7eV [3], still far smaller than the expe-
rimental band gap due to the DFT-GGA scheme tends to
under estimate slightly the bonding group-II oxide poly-
morphs [3,5].
Figure 2. (Color online) Energy band structure of rocksalt
CdO calculated within the DFT-GGA framework. The
shaded region indicates the fundamental gap. The valence
band maximum is chosen as energy zero.
Figure 3. (Color online) Total and partial density of states
of rocksalt CdO.
Nevertheless, GGA does correctly predict an indirect
band gap for the rocksalt CdO with the maxima of the
valence bands occur at the R point and the maxima lie
17

G. YAO ET AL.
above the conduction band minimum at the Γ point,
which results in negative indirect band gap of about
-0.51eV from RVB to ΓCB, indicates rocksalt CdO is a
halfmetal material. In addition, rocksalt CdO may serve
as a transparent conducting material because the bottom
of conduction band in the pattern diffuse with a band-
width 5.52eV fluctuates greatly than that of 1.38eV at the
top of valence band.
By analyzing the partial density of states (PDOS) (see
Figure 3) , it was found that the energy bands between
-17 and -15.5eV mainly consist of O 2s states. The ener-
gy bands at about -7eV consist of Cd 4d states shows a
sharp peak due to its strong localization character. And it
is found that the O 2p states have some admixture with
the Cd sp states. Thus, CdO appears to have some cova-
lent features. There are two peaks at about -3.26eV and
-0.86eV in the upper valence bands. The lower one is
mainly due to O 2p states hybridized with Cd 5s and 4d
states. The upper peak is non-bonding O-2pπ. The con-
duction bands are mostly composed of Cd 5s and 4p and
show a weak hybridization with O 2s and 2p. Taken to-
gether, the energy state density curve near the Fermi lev-
el mainly come from the Cd 4p and O 2p, which deter-
mine the type of charge carrier and the properties of
electric conduction for rocksalt CdO.
Figure 4. (Color online) Charge densities in the (002) plane
of rocksalt CdO.
In order to understand, goes a step further, the micro-
mechanism of both atoms and interatomic, the charge
densities of (002) plane was displayed in Figure 4 to
serve as a complementary tool for achieving a proper
understanding of chemical bonding. We also performed
the Mulliken charge population for rocksalt CdO to un-
derstand bonding behavior. The Mulliken population
results are given in Table 2. The charge transfer from Cd
to O is about 0.8e. It is relative smaller than the charge
population both in Cd and O atoms. Therefore, we con-
cluded that the bonding behavior of rocksalt CdO is a
combination of weaker covalent and stronger ionic na-
tures. And it is mainly contributed by both the O 2p and
the Cd 4d orbits when rocksalt CdO formed.
Table 2. The Mulliken charge population of rocksalt CdO.
Spec i es
Charge population
s p d f Tota l Charge (e)
Cd 0.52 0.69 9.99 - 11.2 +0 .8
O 1.90 4.90 - - 6.8 -0.8
3.2. Optical properties
The linear response of the system to an external electro-
magnetic field with a small wave vector is measured
through the complex dielectric function ε(ω)=
ε1(ω)+iε2(ω), which is mainly connected with the elec-
tronic structures. The imaginary part ε2(ω) of dielectric
function is derived based on the definition of direct tran-
sition [16-18]:
( )( )( )()
( ) kdEE
kjfkifkjpki
m
Ve
kjki
ij
3
2
22
2
2
1
2
ωδ
ω
ωε



−−
⋅−= ∑∫
whe r e
p

is the dipole matrix, |ki> and |kj> are the con-
duction band and valence band wave functions corres-
ponding to the ith and jth eigenvalue with crystal mo-
mentum k. f(ki) and Eki are the Fermi distribution func-
tion and the energy of electron for the
i
th state. The real
part ε1(ω) of the complex dielectric function can be ob-
tained using the Kramers-Krönig relations [16-18]. All
other optical constants, therefore, such as the refractive
index, extinction coefficient, absorption spectrum, refl ec-
tivity and energy loss spectrum can be obtained using the
ε1(ω) and ε2(ω). Those optical spectrums are more con-
venient associate with the microscopic model for the
physic progress, demonstrate the luminescence mechan-
ism of spectrum produced by electron transitions in dif-
ferent energy levels and then characterize the physics
properties for materials much more.
As shown in Fi gure 5, the calculated real part ε1(ω)
and imaginary part ε2(ω) of complex dielectric function
get on well with those reported in Ref. [5]. Especially the
static dielectric function ε1(0) (7.19) tally with the value
(7.20) very well, which suggests that the method in
present work is practicable. As is stated above, however,
the DFT-GGA scheme tends to underestimate slightly the
bonding in the considered group-II oxide polymorphs
[3,5]. Thus, it needs to revise by scissor operator [10] ,
which can correct the band gap and has been successfully
applied to investigate the band gap of TiO2 [19 ], GeO2
[20], etc., to attain considerable accuracy in optical prop-
18

G. YAO ET AL.
erties. The modified results by scissor operator (set to
1.75(∆=Egexp-Egcal=2.3-0.55)) were plot with dotted lines
in Figur e 5. The absorption edge is about 2.23eV corres-
pondence with experimental band gap 2.3eV [21], i.e., it
is necessary and reasonable to correct optical properties
by scissor operator. In this way, we proposes a prediction
value ε1(0)=4.75. Unfortunately, to our knowledge, there
is few experimental and theoretical data of ε1(0) for our
comparison. The real parts ε1(ω) increased rapidly with
the increasing frequency where the photon energy is less
than 2.82eV. The calculated maximum of the ε1(ω) is
about 7.04. The imaginary part ε2(ω) becomes steeper
with an increasing photon energy, which could obtain a
conclusion that the rocksalt CdO could be used as poten-
tial TCOS materials.
Figure 5. (Color online) Real part ε
1(ω) and imaginary part
ε
2(ω) of the dielectric function
ε (ω) of rocksalt CdO.
4. Conclusion
In summary, we calculated the structural parameters,
electronic structure, and optical properties for rocksalt
CdO by means of the DFT within the GGA. Our struc-
tural parameters are in agreement with the previous ex-
perimental date. The electronic structures revealed that
the top of the valence band and the bottom of the con-
duction band are decided by O 2p and Cd 4p states, re-
spectively, and that CdO is a halfmetal material pre-
sented a negative indirect band gap at 2.08 eV in the
RVB-ΓCB direction. Significantly, a more accurate predic-
tion for ε1(0) of about 4.75 was obtained by using the
scissor operator on the basic of our calculated band gap,
suggesting that rocksalt CdO could be used as a potential
TCOS materials. However, there is no experimental data
available related to the rocksalt CdO. Hence, careful ex-
perimental investigations are required in order to clarify
the electronic band structure and optical properties of
rocksalt CdO in detail.
REFERENCES
[1] J.S. Tse, D.D. Klug, S. Desgreniers, J.S. Smith, R. Dutri-
sac, EPL (Europhysics Letters) 86 (2009) 56001.
[2] P.D.C. King, T.D. Veal, A. Schleife, J. Zúñiga-Pérez, B.
Martel, P.H. Jefferson, F. Fuchs, V. Muñoz-Sanjosé, F.
Bechstedt, C. F. McConville, Phys. Rev. B 79 (2009)
205205.
[3] R.J. Guerrero-Moreno, N. Takeuchi, Phys. Rev. B 66
(2002) 205205.
[4] H. Liu, H. Mao, M. Somayazulu, Y. Ding, Y. Meng, D.
Häusermann, Phys. Rev. B 70 (2004) 094114.
[5] A. Schleife, F. Fuchs, J. Furthmüller, F. Bechstedt, Phys.
Rev. B 73 (2008) 245212.
[6] J.E. Jaffe, R. Pandey, A.B. Kunz, Phys. Rev. B 43 (1991)
14030.
[7] J. Zhang, Phys. Chem. Miner. 26 (1999) 644-648.
[8] M. Durandurdu, EPL (Europhysics Letters) 84 (2008)
66003.
[9] L.F.J. Piper, A. DeMasi, K.E. Smith, A. Schleife, F.
Fuchs, F. Bechstedt, J. Zuniga-Perez, V. Munoz-Sanjosé,
Phys. Rev. B 77 (2008) 125204.
[10] P. Dufek, P. Blaha, K. Schwarz, Phys. Rev. B 50 (1994)
7279.
[11] M.D. Segall, P.J.D. Lindan, M.J. Probert, C.J. Pickard,
P.J. Hasnip, S.J. Clark, M.C. Payne, J. Phys.: Condens.
Matter 14 (2002) 2717.
[12] Y. Wang, J.P. Perdew, Phys. Rev. B 44 (1991) 13298.
[13] H.J. Monkhorst, J.D. Pack, Phys. Rev. B 13 (1976) 5188.
[14] Cimino, M. Marezio, J. Phys. Chem. Solids 17 (1960)
57-64.
[15] F. Birch, Phys. Rev. 71 ( 1947) 809.
[16] X.C. Shen, The Spectrum and Optical Property of Semi-
conductor, Science Press, Beijing, 1992.
[17] C.M.I. Okoye, J. Phys.: Condens. Matter 15 (2003) 5945.
[18] M.Q. Cai, Z. Yin, M.S. Zhang, Appl. Phys. Lett. 83 (2003)
2805.
[19] R. Asahi, Y. Taga, W. Mannstadt, A. J. Freeman, Phys.
Rev. B 61 (2000) 7459.
[20] Q.J. Liu, Z.T. Liu, L.P. Feng, H. Tian, Solid State Sci. 12
(2010) 1748.
[21] F.P. Koffyberg, Phys. Rev. B 13 (1976) 447
19