ABSTRACT

We establish some results on coincidence and common fixed point for a two pair of multi-valued and single-valued maps in ultra metric spaces.

1. Introduction

Roovij in [1] introduced the concept of ultra metric space. Later, C. Petalas, F. Vidalis [2] and Ljiljana Gajic [3] studied fixed point theorems of contractive type maps on a spherically complete ultra metric spaces which are generalizations of the Banach fixed point theorems. In [4] K. P. R. Rao, G. N. V. Kishore and T. Ranga Rao obtained two coincidence point theorems for three or four self maps in ultra metric space.

J. Kubiaczyk and A. N. Mostafa [5] extend the fixed point theorems from the single-valued maps to the setvalued contractive maps. Then Gajic [6] gave some generalizations of the result of [3]. Again, Rao [7] proved some common fixed point theorems for a pair of maps of Jungck type on a spherically complete ultra metric space.

In this article, we are going to establish some results on coincidence and common fixed point for two pair of multi-valued and single-valued maps in ultra metric spaces.

2. Basic Concept

First we introducing a notation.

Let 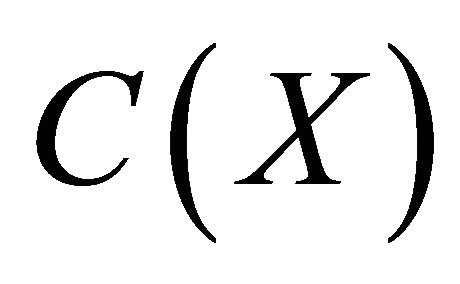denote the class of all non empty compact subsets of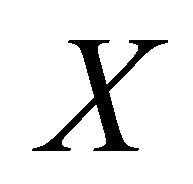. For, the Hausdorff metric is defined as

where.

The following definitions will be used later.

Definition 2.1 ([1]) Letbe a metric space. If the metric satisfies strong triangle inequality

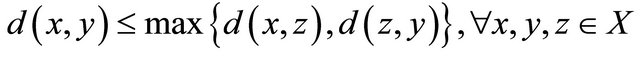
Then is called an ultra metric on and is called an ultra metric space.

Example. Let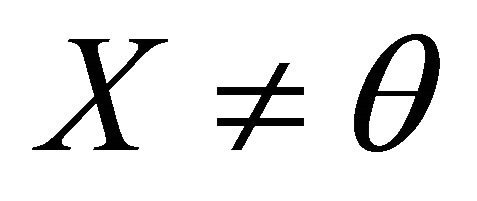, , then

is a ultra metric space.

Definition 2.2 ([1]) An ultra metric space is said to be spherically complete if every shrinking collection of balls in has a non empty intersection.

Definition 2.3 An elementis said to be a coincidence point of and if. We denote

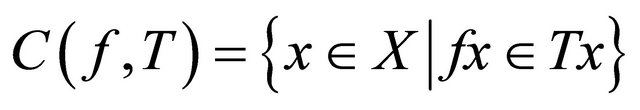
the set of coincidence points of and.

Definition 2.4 ([7]) Let be an ultra metric space, and. and are said to be coincidentally commuting at 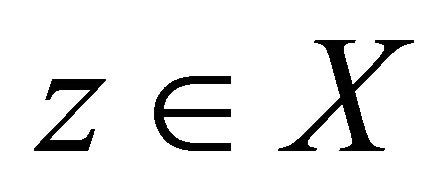if implies.

Definition 2.5 ([8]) An element is a common fixed point of and if .

3. Main Results

The following results are the main result of this paper.

Theorem 3.1 Let 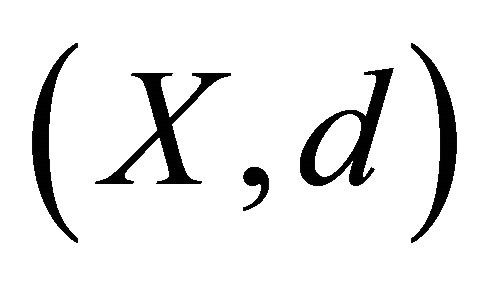be an ultra metric space. Let be a pair of multi-valued maps and a pair of single-valued maps satisfying

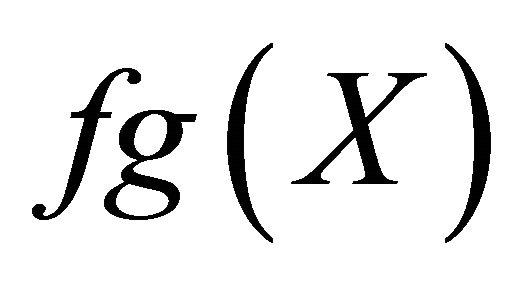(a) is spherically complete;

(b)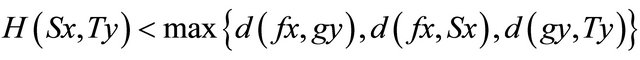

for all, with;

(c) ;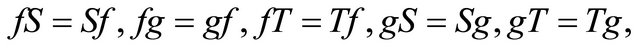

(d).

Then there exist point and in, such that

.

Proof. Let

denote the closed sphere with centeredand radius

.

Let be the collection of all the spheres for all.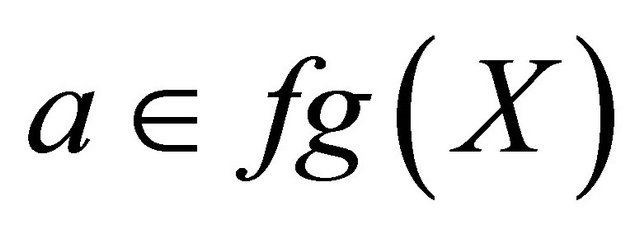

Then the relation

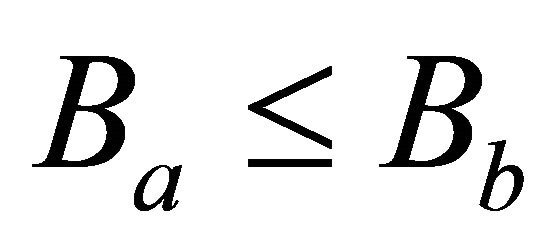if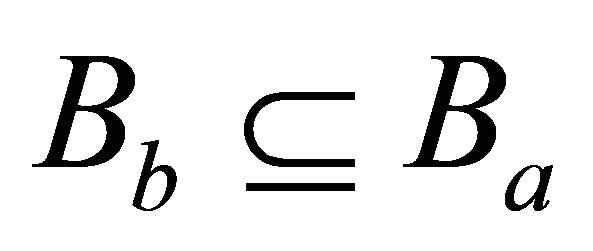

is a partial order on.

Consider a totally ordered sub family of.

Since 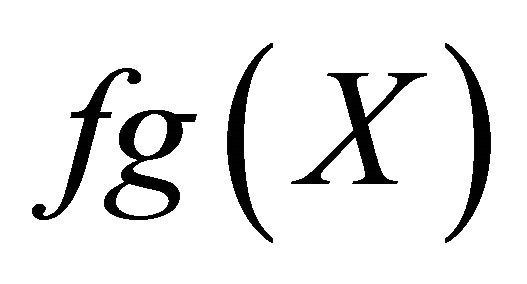is spherically complete, we have

Let where and.

Then. Hence

(1)

If then. Assume that.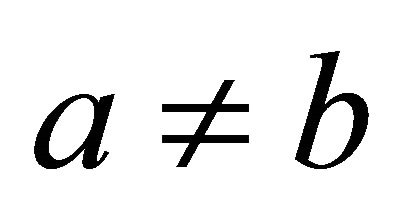

Let, then

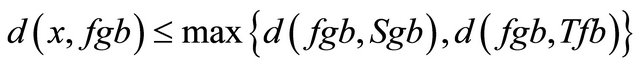
Sinceis nonempty compact set, then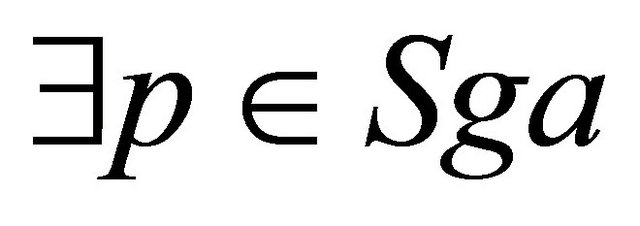 such that

;

is a nonempty compact set, then such that.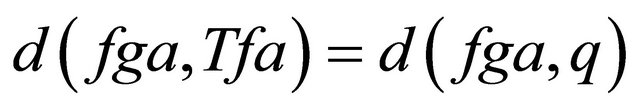

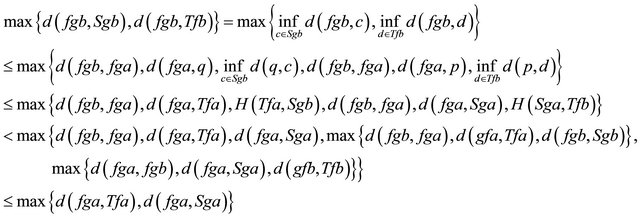
from (a) (b) and Equation (1)

Now

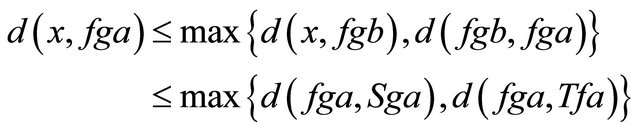
So, we have just proved that for every. Thus is an upper bound in for the family and hence by Zorn’s Lemma, there is a maximal element in, say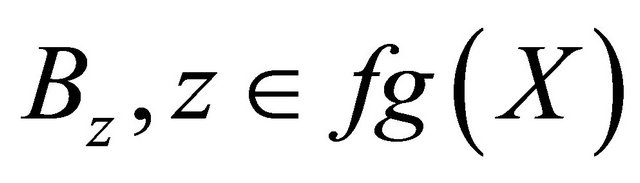. There exists such that.

Suppose

.

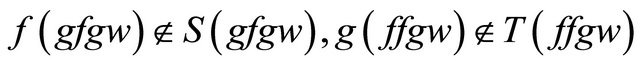Since are nonempty compact sets, then such that

(2)

(3)

From (b), (c) and Equation (2), we have

(4)

(5)

From (b), (c) and Equations (2)-(5)

(6)

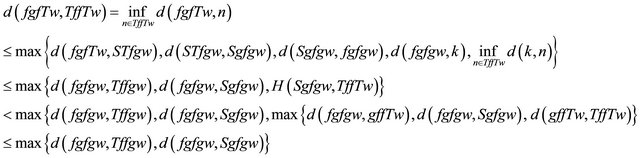(7)

From Equation (4) and Equation (6) we have

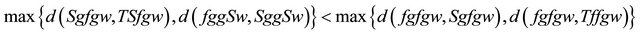(8)

From Equation (5) and Equation (7) we have

(9)

If

Then from Equation (8),. Hence. It is a contradiction to the maximality of in, since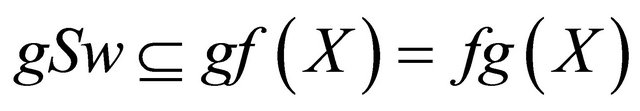

If

Then from Equation (9),. Hence.It is a contradiction to the maximality of 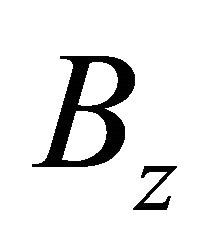in, since.

So

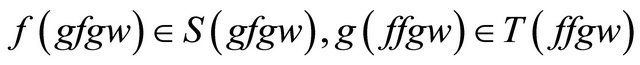(10)

In addition,.

Using (b), (c) and Equation (10), we obtain

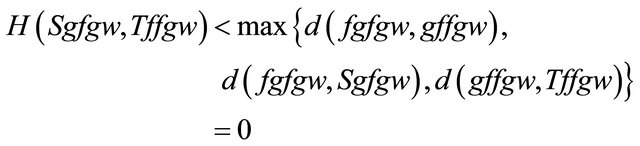
Hence.

Then the proof is completed.

Theorem 3.2 Let be an ultra metric space. Let 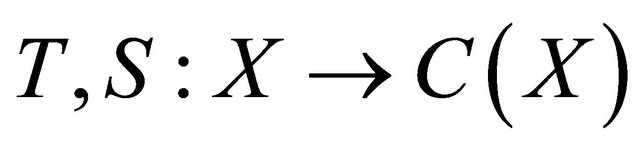be a pair of multi-valued maps and be a single-valued maps satisfying

(a) is spherically complete;

(b)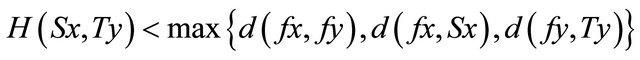

for all,with;

(c);

(d).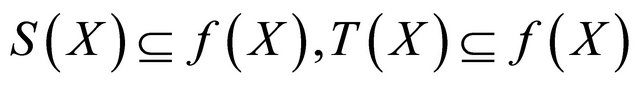

Then 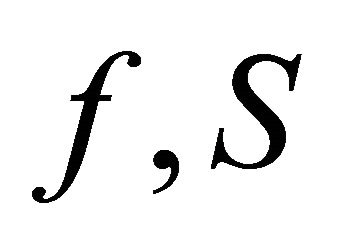and have a coincidence point in.

Moreover, if and, and are coincidentally commuting at and, then and have a common fixed point in.

Proof. If in Theorem 2.1, we obtain that there exist points and in such that

.

As, and ipipare coincidentally commuting at and.

Write, then.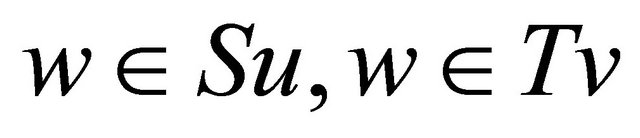

Then we have

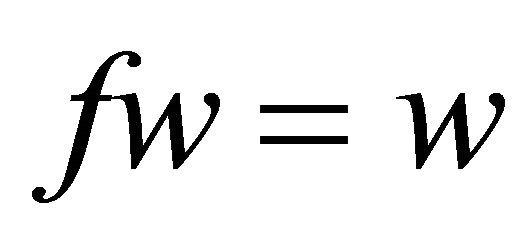
and

.

Now, since also, and are coincidentally commuting at and, so we obtain

.

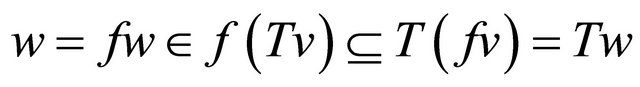Thus, we have proved that, that is, is a common fixed point of and.

Corollary 3.3 Let be a spherically complete ultra metric space. Let be a pair of multi-valued maps satisfying

(a) for all,with;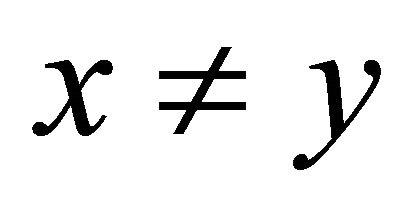

(b).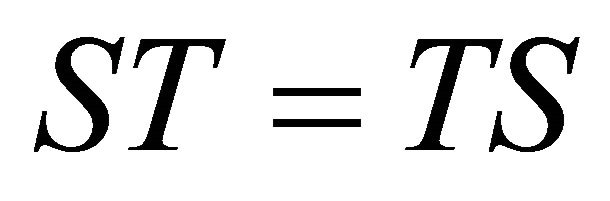

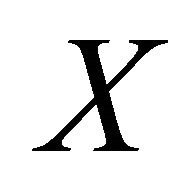Then, there exists a pointinsuch that and.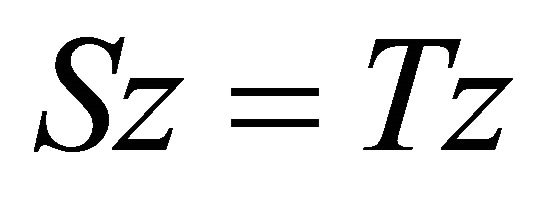

Remark 1 If 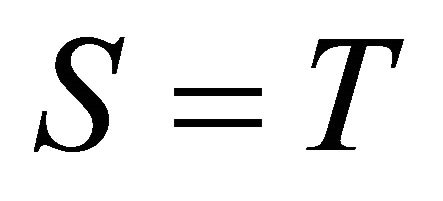in Corollary 3.3, then we obtain the Theorem of Ljiljana Gajic [6].

Remark 2 If in Theorem 3.1, , we obtain Theorem 9 of K. P. R. Rao at [7].

Remark 3 Ifandin Theorem 3.1 are single-valued maps, then: 1) we obtain the results of K. P. R. Rao [4]; 2)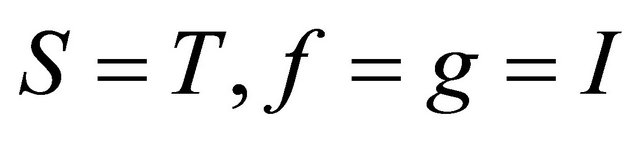, we obtain the result of Ljiljana Gajic [3]; 3), then, we obtain Theorem 4 of K. P. R. Rao at [7].

4. Conclusion

In this paper, we get coincidence point theorems and common fixed point theorems for two pair of multi-valued and single-valued maps satisfying different contractive conditions on spherically complete ultra metric space, which is generalized results of [3-7].

5. Acknowledgements

Foundation item: Science and Technology Foundation of Educational Committee of Tianjin (11026177).

REFERENCES

NOTES

^*Corresponding author.