Open Journal of Discrete Mathematics
Vol.4 No.3(2014), Article
ID:47452,7
pages
DOI:10.4236/ojdm.2014.43009
Some Results on Prime Labeling*
U. M. Prajapati1, S. J. Gajjar2
1St. Xaviers College, Ahmedabad, India
2Government Polytechnic, Himmatnagar, India
Email: udayan64@yahoo.com, gjr.sachin@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 May 2014; revised 5 June 2014; accepted 24 June 2014
ABSTRACT
In the present work we investigate some classes of graphs and disjoint union of some classes of graphs which admit prime labeling. We also investigate prime labeling of a graph obtained by identifying two vertices of two graphs. We also investigate prime labeling of a graph obtained by identifying two edges of two graphs. Prime labeling of a prism graph is also discussed. We show that a wheel graph of odd order is switching invariant. A necessary and sufficient condition for the complement of  to be a prime graph is investigated.
to be a prime graph is investigated.
Keywords:Graph Labeling, Prime Labeling, Switching of a Vertex, Switching Invariance

1. Introduction
We begin with simple, finite, undirected and non-trivial graph  with the vertex set
with the vertex set ![]() and the edge set
and the edge set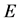 . The number of elements of
. The number of elements of![]() , denoted as
, denoted as ![]() is called the order of the graph
is called the order of the graph ![]() while the number of elements of
while the number of elements of![]() , denoted as
, denoted as ![]() is called the size of the graph
is called the size of the graph![]() . In the present work
. In the present work ![]() denotes the cycle with
denotes the cycle with ![]() vertices and
vertices and 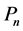 denotes the path of
denotes the path of ![]() vertices. In the wheel
vertices. In the wheel  the vertex corresponding to
the vertex corresponding to  is called the apex vertex and the vertices corresponding to
is called the apex vertex and the vertices corresponding to ![]() are called the rim vertices. For various graph theoretic notations and terminology we follow Gross and Yellen [1] whereas for number theory we follow D. M. Burton [2] . We will give brief summary of definitions and other information which are useful for the present investigations.
are called the rim vertices. For various graph theoretic notations and terminology we follow Gross and Yellen [1] whereas for number theory we follow D. M. Burton [2] . We will give brief summary of definitions and other information which are useful for the present investigations.
Definition 1.1: If the vertices of the graph are assigned values subject to certain conditions then it is known as graph labeling.
For latest survey on graph labeling we refer to J. A. Gallian [3] . Vast amount of literature is available on different types of graph labeling and more than 1000 research papers have been published so far in last four decades. For any graph labeling problem following three features are really noteworthy:
Ÿ a set of numbers from which vertex labels are chosen;
Ÿ a rule that assigns a value to each edge;
Ÿ a condition that these values must satisfy.
The present work is aimed to discuss one such labeling known as prime labeling.
Definition 1.2: A prime labeling of a graph ![]() of order
of order ![]() is an injective function
is an injective function  such that for every pair of adjacent vertices
such that for every pair of adjacent vertices ![]() and
and![]() ,
,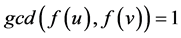 . The graph which admits prime labeling is called a prime graph.
. The graph which admits prime labeling is called a prime graph.
The notion of prime labeling was originated by Entringer and was discussed in A.Tout [4] . Many researchers have studied prime graphs. It has been proved by H. L. Fu and C. K. Huang [5] that  is a prime graph. It has been proved by S. M. Lee [6] that wheel graph
is a prime graph. It has been proved by S. M. Lee [6] that wheel graph ![]() is a prime graph if and only if
is a prime graph if and only if ![]() is even. T. Deretsky [7] has proved that cycle
is even. T. Deretsky [7] has proved that cycle ![]() is a prime graph.
is a prime graph.
Definition 1.3: A vertex switching  of a graph
of a graph ![]() is the graph obtained by taking a vertex
is the graph obtained by taking a vertex ![]() of
of![]() , removing all the edges incident to
, removing all the edges incident to ![]() and adding edges joining to every other vertex which is not adjacent to
and adding edges joining to every other vertex which is not adjacent to ![]() in
in![]() .
.
Definition 1.4: A prime graph is said to be switching invariant if for every vertex ![]() of
of![]() , the graph
, the graph  obtained by switching the vertex
obtained by switching the vertex ![]() in
in ![]() is also a prime graph.
is also a prime graph.
Definition 1.5: For two graphs  and
and 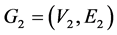 their cartesian product
their cartesian product  is defined as the graph whose vertex set is
is defined as the graph whose vertex set is  and two vertices
and two vertices  and
and  in
in 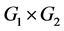 are adjacent if
are adjacent if  and
and ![]() is adjacent to
is adjacent to ![]() or
or ![]() is adjacent to
is adjacent to  and
and .
.
Definition 1.6:  is called prism graph.
is called prism graph.
Bertrand’s Postulate 1.7: For every positive integer 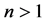 there is a prime
there is a prime ![]() such that
such that![]() .
.
2. Some Results on Prime Labeling
Theorem 2.1: If  is a prime graph with order
is a prime graph with order![]() , where
, where ![]() is even and
is even and ![]() is a graph with order 3 then disjoint union of
is a graph with order 3 then disjoint union of 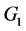 and
and ![]() is a prime graph.
is a prime graph.
Proof: Let 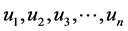 be the vertices of
be the vertices of 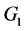 and
and  be the vertices of
be the vertices of![]() . Let
. Let ![]() be a disjoint union of
be a disjoint union of  and
and![]() . Now
. Now  is a prime graph, so there is an injective function
is a prime graph, so there is an injective function  such that for any arbitrary edge
such that for any arbitrary edge , we have
, we have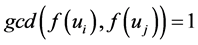 .
.
Define a function  as follows:
as follows:

Clearly ![]() is an injective function.
is an injective function.
If  is any edge of
is any edge of ![]() then
then . If
. If 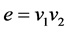 then
then
 . If
. If 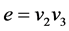 then
then . If
. If
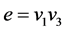 then
then  as
as ![]() is even.
is even.
Thus ![]() admits a prime labeling. So
admits a prime labeling. So ![]() is a prime graph.
is a prime graph.
Theorem 2.2: If  is a prime graph with order
is a prime graph with order![]() , where
, where ![]() is divisible by 6 and
is divisible by 6 and ![]() is a prime graph with order 5 then disjoint union of
is a prime graph with order 5 then disjoint union of  and
and ![]() is a prime graph.
is a prime graph.
Proof: Let 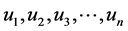 be the vertices of
be the vertices of 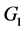 and
and  be the vertices of
be the vertices of![]() . Let
. Let ![]() be the disjoint union of
be the disjoint union of  and
and![]() . Now
. Now  is a prime graph, so there exists an injective function
is a prime graph, so there exists an injective function
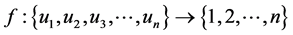 such that for any arbitrary edge
such that for any arbitrary edge 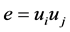 of
of ,
, . Also
. Also ![]() is a prime graph, so there is an injective function
is a prime graph, so there is an injective function  such that for any arbitrary edge
such that for any arbitrary edge  of
of![]() ,
, . Define a function
. Define a function  as follows:
as follows:

Clearly  is an injective function. To prove
is an injective function. To prove  is a prime labeling of
is a prime labeling of ![]() we have the following cases:
we have the following cases:
Case 1: If 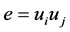 is any edge of
is any edge of  then
then .
.
Case 2: Suppose  is any edge of
is any edge of ![]() and
and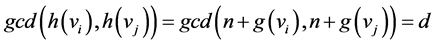 . Here
. Here
![]() is an odd natural number as
is an odd natural number as ![]() is even and at least one of
is even and at least one of  and
and  is odd. As
is odd. As 
and 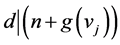 so
so . But possible values of
. But possible values of 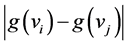 are 1, 2, 3 and 4, and
are 1, 2, 3 and 4, and ![]() is odd. So
is odd. So 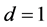 or
or . If
. If  then
then  and
and . Also
. Also , therefore
, therefore ![]() and
and , which is not possible as
, which is not possible as . Thus
. Thus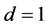 , hence
, hence .
.
Thus ![]() admits prime labeling. So
admits prime labeling. So ![]() is a prime graph.
is a prime graph.
S. K. Vaidya and U. M. Prajapati [8] has proved that if  is an even integer and
is an even integer and  is a natural number, then the graph obtained by identifying any of the rim vertices of a wheel
is a natural number, then the graph obtained by identifying any of the rim vertices of a wheel  with an end vertex of a path graph
with an end vertex of a path graph  is a prime graph. But in the following theorem we have prove that if
is a prime graph. But in the following theorem we have prove that if ![]() is odd then also it is prime.
is odd then also it is prime.
Theorem 2.3: If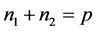 , where
, where ![]() is prime then the graph obtained by identifying one of the rim vertices of
is prime then the graph obtained by identifying one of the rim vertices of 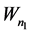 with an end vertex of
with an end vertex of  is prime.
is prime.
Proof: Let  be an apex vertex of
be an apex vertex of  and
and  be consecutive rim vertices of
be consecutive rim vertices of  and
and  are consecutive vertices of
are consecutive vertices of . Without loss of generality we can assume that
. Without loss of generality we can assume that  be the graph obtained by identifying a rim vertex
be the graph obtained by identifying a rim vertex ![]() of
of  with an end vertex
with an end vertex ![]() of
of . Define
. Define  as follows:
as follows:

Clearly ![]() is an injective function. Let
is an injective function. Let ![]() be an arbitrary edge of
be an arbitrary edge of![]() . To prove
. To prove ![]() is a prime labeling of
is a prime labeling of ![]() we have the following cases:
we have the following cases:
Case 1: If  then
then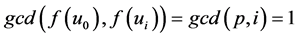 ,
, .
.
Case 2: If  then
then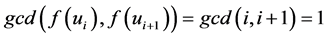 ,
, .
.
Case 3: If  then
then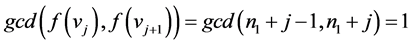 ,
, .
.
Case 4: If  then
then .
.
Case 5: If  then
then 
Thus ![]() admits a prime labeling. So
admits a prime labeling. So ![]() is a prime graph.
is a prime graph.
Theorem 2.4: A path  and
and ![]() copies of cycle
copies of cycle ![]() are given, then the graph obtained by identifying each edge of
are given, then the graph obtained by identifying each edge of  with an edge of a corresponding copy of the cycle
with an edge of a corresponding copy of the cycle ![]() is prime.
is prime.
Proof: Let  be the vertex of
be the vertex of  and
and  be the vertices of
be the vertices of  copy of cycle
copy of cycle ![]() where
where . Let
. Let ![]() be a graph obtained by identifying an edge
be a graph obtained by identifying an edge  of
of  copy of cycle
copy of cycle ![]() with an edge
with an edge  of path
of path , where
, where . Let
. Let ![]() be the set of vertices of
be the set of vertices of ![]() then
then . Define a function
. Define a function 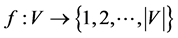 as follows:
as follows:
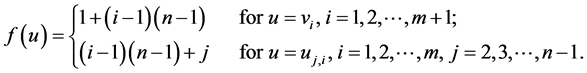
Clearly ![]() is an injective function. Let
is an injective function. Let ![]() be an arbitrary edge of
be an arbitrary edge of![]() . To prove
. To prove ![]() is a prime labeling of
is a prime labeling of ![]() we have the following cases:
we have the following cases:
Case 1: If  then
then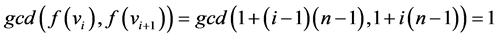 , for
, for .
.
Case 2: If  then
then , for
, for ![]() and
and .
.
Case 3: If 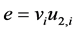 then
then .
.
Case 4: If 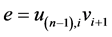 then
then .
.
Thus ![]() is a prime graph. So
is a prime graph. So ![]() is a prime graph.
is a prime graph.
Theorem 2.5: A cycle  and
and ![]() copies of a cycle
copies of a cycle ![]() are given, then the graph obtained by identifying each edge of
are given, then the graph obtained by identifying each edge of  with an edge of corresponding copy of the cycle
with an edge of corresponding copy of the cycle ![]() is prime.
is prime.
Proof: Let  be the vertices of
be the vertices of  and
and  be the vertices of
be the vertices of  copy of cycle
copy of cycle ![]() where
where . Let
. Let ![]() be a graph obtained by identifying an edge
be a graph obtained by identifying an edge 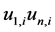 of
of 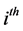 copy of cycle
copy of cycle ![]() with an edge
with an edge  of cycle
of cycle , where
, where  and an edge
and an edge  of
of  copy of cycle
copy of cycle ![]() with an edge
with an edge  of cycle
of cycle 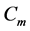 . Let
. Let ![]() be the vertex set of
be the vertex set of ![]() then
then . Define a function
. Define a function 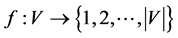 as follows:
as follows:

Clearly ![]() is an injective function. Let
is an injective function. Let ![]() be an arbitrary edge of
be an arbitrary edge of![]() . To prove
. To prove ![]() is a prime labeling of
is a prime labeling of ![]() we have the following cases:
we have the following cases:
Case 1: If  then
then , for
, for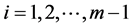 .
.
Case 2: If  then
then .
.
Case 3: If  then
then , for
, for ![]() and
and .
.
Case 4: If ,
,  , for
, for .
.
Case 5: If 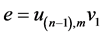 then
then .
.
Case 6: If  then
then , for
, for  .
.
Thus ![]() admits a prime labeling. So
admits a prime labeling. So ![]() is a prime graph.
is a prime graph.
S. K. Vaidya and U. M. Prajapati [9] have proved that switching the apex vertex in ![]() is a prime graph and switching a rim vertex in
is a prime graph and switching a rim vertex in ![]() is a prime graph if
is a prime graph if  is prime. But in the following theorem we have proved that
is prime. But in the following theorem we have proved that ![]() is switching invariant if
is switching invariant if ![]() is even.
is even.
Theorem 2.6: 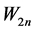 is switching invariant.
is switching invariant.
Proof: Let  be rim vertices and
be rim vertices and ![]() be an apex vertex of
be an apex vertex of . According to the degree of vertices of
. According to the degree of vertices of  we can take the following cases.
we can take the following cases.
Case 1: Let ![]() be a graph obtained by switching a rim vertex
be a graph obtained by switching a rim vertex . Let
. Let ![]() be a largest prime less than
be a largest prime less than![]() .
.
Define a function  as follows:
as follows:

Clearly ![]() is an injective function. Let
is an injective function. Let ![]() be an arbitrary edge of
be an arbitrary edge of![]() . To prove
. To prove ![]() is a prime labeling of
is a prime labeling of ![]() we have the following cases:
we have the following cases:
Ÿ If ,
,  then
then .
.
Ÿ If ,
, ![]() then
then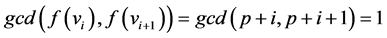 .
.
Ÿ If  then
then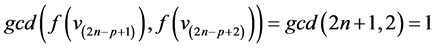 .
.
Ÿ If ,
, ![]() then
then  .
.
Ÿ If ,
,  then
then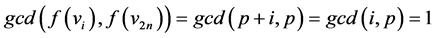 , as
, as ![]() is the largest prime less than
is the largest prime less than![]() .
.
Case 2: Let ![]() be a graph obtained by switching an apex vertex
be a graph obtained by switching an apex vertex![]() .
.
Define a function  as follows:
as follows:

Clearly ![]() is an injective function. It can be easily verified that
is an injective function. It can be easily verified that ![]() is a prime labeling.
is a prime labeling.
Thus from both the cases it follows that ![]() is a prime graph.
is a prime graph.
Theorem 2.7: The complement of ![]() is prime if and only if
is prime if and only if 
Proof: We can easily see that 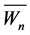 is prime for
is prime for 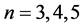 and 6 from Figure 1.
and 6 from Figure 1.
Now if 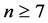 then
then  and every rim vertex of
and every rim vertex of  is adjacent to other
is adjacent to other  rim vertices. We have total
rim vertices. We have total  even numbers to assign
even numbers to assign  vertices. If one of the rim vertices is labeled as even number then other
vertices. If one of the rim vertices is labeled as even number then other  vertices can not be labeled as even number. Also remaining two rim vertices are adjacent, so only one of them can be labeled as even number. The apex vertex can also be labeled as even number. Thus maximum three vertices can be labeled as even number. But if
vertices can not be labeled as even number. Also remaining two rim vertices are adjacent, so only one of them can be labeled as even number. The apex vertex can also be labeled as even number. Thus maximum three vertices can be labeled as even number. But if  then we have 4 or more even numbers to label. So it is not possible. Thus
then we have 4 or more even numbers to label. So it is not possible. Thus 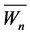 is not prime for
is not prime for .
.
Theorem 2.8: Let ![]() be a prime number and take
be a prime number and take ![]() copies of
copies of , then the graph obtained by identifying one vertex of each copy of
, then the graph obtained by identifying one vertex of each copy of  with corresponding pendant vertex of
with corresponding pendant vertex of 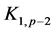 is prime.
is prime.
Proof: Let  be an apex vertex and
be an apex vertex and  be pendant vertices of
be pendant vertices of . Also let
. Also let 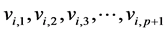 be the vertices of
be the vertices of  copy of
copy of . Now let
. Now let ![]() be the graph obtained by identifying a pendant vertex
be the graph obtained by identifying a pendant vertex ![]() of
of  with a vertex
with a vertex 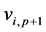 of
of  copy of
copy of , where
, where![]() .
.
Define a function , where
, where 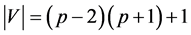 as follows:
as follows:

Clearly ![]() is an injective function. Let
is an injective function. Let ![]() be an arbitrary edge of
be an arbitrary edge of![]() . To prove
. To prove ![]() is a prime labeling of
is a prime labeling of ![]() we have the following cases:
we have the following cases:
Case 1: If ,
,  , for
, for![]() .
.
Case 2: If ,
, 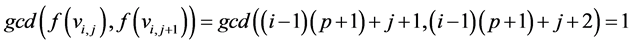 for
for ![]() and
and![]() .
.
Case 3: If  then for
then for ![]() and
and![]() ,
,


Figure 1. Prime labeling of  and
and![]() .
.
Thus ![]() admits a prime labeling. So
admits a prime labeling. So ![]() is a prime graph.
is a prime graph.
Theorem 2.9: If  is an odd integer then the prism graph
is an odd integer then the prism graph  is not prime.
is not prime.
Proof: In the prism graph 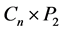 there are two cycles
there are two cycles![]() . So total number of vertices are
. So total number of vertices are![]() . So we have to use 1 to
. So we have to use 1 to ![]() natural numbers to label these vertices, and from 1 to
natural numbers to label these vertices, and from 1 to ![]() there are
there are ![]() even integers. If
even integers. If ![]() is odd then we can use at the most
is odd then we can use at the most 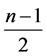 even integers to label the vertices of a cycle
even integers to label the vertices of a cycle![]() . We have such two cycles, so we can use at the most
. We have such two cycles, so we can use at the most  even integers to label the vertices of
even integers to label the vertices of . But from 1 to
. But from 1 to ![]() there are
there are ![]() even integers. So such prime labeling is not possible.
even integers. So such prime labeling is not possible.
Thus  is not prime if
is not prime if  is an odd integer.
is an odd integer.
Theorem 2.10: If ![]() is a prime number then the prism graph
is a prime number then the prism graph  is prime.
is prime.
Proof: In the prism graph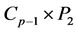 , let
, let 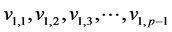 be the vertices of one cycle and
be the vertices of one cycle and ,
,
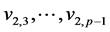 be the vertices of the other cycle and a vertex
be the vertices of the other cycle and a vertex ![]() is joined with
is joined with  by an edge for
by an edge for
![]() . Define a function
. Define a function  as follows:
as follows:

Clearly ![]() is an injective function. Let
is an injective function. Let ![]() be an arbitrary edge of
be an arbitrary edge of![]() . To prove
. To prove ![]() is a prime labeling of
is a prime labeling of ![]() we have the following cases:
we have the following cases:
Case 1: If  then
then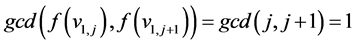 , for
, for![]() .
.
Case 2: If  then
then , for
, for![]() .
.
Case 3: If  then
then .
.
Case 4: If  then
then .
.
Case 5: If  then
then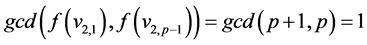 .
.
Case 6: If 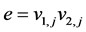 then
then , for
, for![]() .
.
Case 7: If 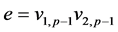 then
then .
.
Thus ![]() admits a prime labeling. So
admits a prime labeling. So ![]() is a prime graph.
is a prime graph.
Theorem 2.11: A graph obtained by joining every rim vertex of a wheel graph 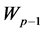 with corresponding vertex of a cycle
with corresponding vertex of a cycle  is a prime graph, where
is a prime graph, where ![]() is a prime number not less than 3.
is a prime number not less than 3.
Proof: Let ![]() be an apex vertex and
be an apex vertex and  be rim vertices of
be rim vertices of . Also
. Also  are the vertices of
are the vertices of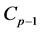 . Let
. Let ![]() be the graph obtained by joining a vertex
be the graph obtained by joining a vertex ![]() of
of  with a vertex
with a vertex ![]() of
of  by an edge, where
by an edge, where![]() . Define a function
. Define a function  as follows:
as follows:

Clearly ![]() is an injective function. Let
is an injective function. Let ![]() be an arbitrary edge of
be an arbitrary edge of![]() . To prove
. To prove ![]() is a prime labeling of
is a prime labeling of ![]() we have the following cases:
we have the following cases:
Case 1: If  then
then , for
, for![]() .
.
Case 2: If  then
then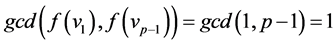 .
.
Case 3: If  then
then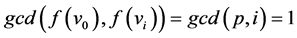 , for
, for![]() .
.
Case 4: If 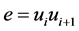 then
then , for
, for![]() .
.
Case 5: If 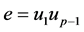 then
then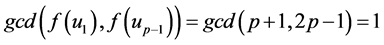 .
.
Case 6: If  then
then , for
, for![]() .
.
Thus ![]() admits a prime labeling. So
admits a prime labeling. So ![]() is a prime graph.
is a prime graph.
3. Concluding Remarks
Study of relatively prime numbers is very interesting in the theory of numbers and it is challenging to investigate prime labeling of some families of graphs. Here we investigate several results of some classes of graphs about prime labeling. Extending the study to other graph families is an open area of research.
Acknowledgements
The authors are highly thankful to the anonymous referee for valuable comments and constructive suggestions on the first draft of this paper.
References
- Gross, J. and Yellen, J. (2004) Handbook of Graph Theory, CRC Press, Boca Raton.
- Burton, D.M. (2007) Elementary Number Theory. 6th Edition, Tata McGraw-Hill Publishing Company Limited, New Delhi.
- Gallian, J.A. (2012) A Dynamic Survey of Graph Labeling. The Electronic Journal of Combinatorics, 19, # DS6.
- Tout, A., Dabboucy, A.N. and Howalla, K. (1982) Prime Labeling of Graphs. National Academy Science Letters, 11, 365-368.
- Fu, H.L. and Huang, K.C. (1994) On Prime Labellings. Discrete Mathematics, 127, 181-186. http://dx.doi.org/10.1016/0012-365X(92)00477-9
- Lee, S.M., Wui, I. and Yeh, J. (1988) On the Amalgamation of Prime Graphs. Bull. of Malaysian Math. Soc., 11, 59-67.
- Deretsky, T., Lee, S.M. and Mitchem, J. (1991) On Vertex Prime Labelings of Graphs. In: Alvi, J., Chartrand, G., Oellerman, O. and Schwenk, A., Eds., Graph Theory, Combinatorics and Applications. Proceedings of the 6th International Conference Theory and Applications of Graphs, Wiley, New York, 359-369.
- Vaidya, S.K. and Prajapati, U.M. (2011) Some Results on Prime and K-Prime Labeling. Journal of Mathematics Research, 3, 66-75. http://dx.doi.org/10.5539/jmr.v3n1p66
- Vaidya, S.K. and Prajapati, U.M. (2012) Some Switching Invariant Prime Graphs. Open Journal of Discrete Mathematics, 2, 17-20. http://dx.doi.org/10.4236/ojdm.2012.21004
NOTES

*AMS subject classification number: 05C78.

