Applied Mathematics
Vol.06 No.08(2015), Article ID:58298,15 pages
10.4236/am.2015.68124
Forced Oscillation of Solutions of a Fractional Neutral Partial Functional Differential Equation
V. Sadhasivam, J. Kavitha*
Post Graduate and Research Department of Mathematics, Thiruvalluvar Government Arts College, Rasipuram, Namakkal Dt. Tamil Nadu, India
Email: ovsadha@gmail.com, *kaviakshita@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 June 2015; accepted 20 July 2015; published 24 July 2015
ABSTRACT
In this paper, we will establish the sufficient conditions for the oscillation of solutions of neutral time fractional partial differential equation of the form
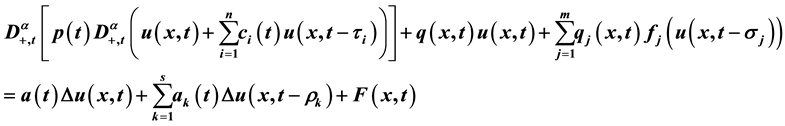
for  where
where 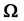 is a bounded domain in
is a bounded domain in 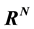 with a piecewise smooth boundary
with a piecewise smooth boundary 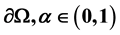 is a constant,
is a constant, 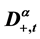 is the Riemann-Liouville fractional derivative of order
is the Riemann-Liouville fractional derivative of order 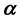 of u with respect to t and
of u with respect to t and 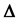 is the Laplacian operator in the Euclidean N-space
is the Laplacian operator in the Euclidean N-space  subject to the condition
subject to the condition 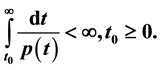
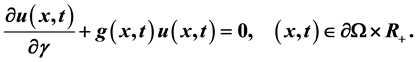
Keywords:
Fractional, Neutral, Oscillation, Partial, Functional

1. Introduction
Fractional differential equations are generalizations of classical differential equations to an arbitrary non integer order and have gained considerable importance due to the fact that these equations are applied in real world problems arising in various branches of science and technology [1] -[5] . Neutral delay differential equations have applications in electric networks containing Lossless transmission lines and population dynamics [6] . Several papers concerning neutral parabolic differential equations have appeared recently (for example see [7] [8] ). The oscillatory theory of solutions of fractional differential equations has received a great deal of attention [9] - [15] . In the last few years, many authors studied the oscillation of a time-fractional partial differential equations [16] [17] . There are only few works has been done on oscillation of forced neutral fractional partial differential equations.
In this paper, we study the oscillatory behavior of solutions of nonlinear neutral fractional differential equations with forced term of the form
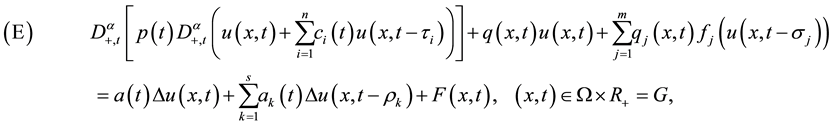
where  is a bounded domain in
is a bounded domain in  with a piecewise smooth boundary
with a piecewise smooth boundary 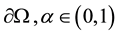 is a constant,
is a constant, 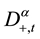 is the Riemann-Liouville fractional derivative of order
is the Riemann-Liouville fractional derivative of order 





(B1)
where 



(B2)
In what follows, we always assume without mentioning that
(A1) 
(A2)


(A3) 
(A4)




(A5) 


(A6) 
A function 





2. Preliminaries
In this section, we give the definitions of fractional derivatives and integrals and some notations which are useful throughout this paper. There are several kinds of definitions of fractional derivatives and integrals. In this paper, we use the Riemann-Liouville left sided definition on the half-axis

Definition 2.1. The Riemann-Liouville fractional partial derivative of order 


provided the right hand side is point wise defined on 

Definition 2.2. The Riemann-Liouville fractional integral of order 



provided the right hand side is pointwise defined on
Definition 2.3. The Riemann-Liouville fractional derivative of order 



provided the right hand side is pointwise defined on 


Lemma 2.1. Let 
Then
3. Oscillation of (E), (B1)
We introduce a class of function P. Let
The function 

C1) 


C2) 


Lemma 3.1. If 




with 

Proof. Let 



Using Green’s formula and boundary condition (B1) it follows that

and

Also from (A3), (A5), we obtain

and using and Jensen’s inequality we get

In view of (1), (7)-(10) and A6, (6) yield
This completes the proof.
Lemma 3.2. Let 



1)
2) 
Proof. From Lemma 3.1, the function 




for 

Lemma 3.3. Let 


Proof. From Case (I), 




This completes the proof.
Lemma 3.4. Let 


Proof. In this case the function 





This completes the proof.
Theorem 3.1. Assume that 



be continuous functions such that 

Assume also that there exists a positive nondecreasing function 

where
and

where 

Then every solution 

Proof. Suppose that 









Let 

Case (I): For this case 


Define the function 

then

From 




Let 



substituting 





Thus for all

Then, by (22) and (C2), for 

Then, by (14) and (C2), we have

which contradicts (14).
Case (II): Assume that 

Let 



Integrating (26) from 

condition (15) implies that the last inequality has no eventually positive solution, a contradiction. This completes the proof.
Corollary 3.1. Let conditions of Theorem 3.1 be hold. If the inequality (16) has no eventually positive solutions, then every solution 

Corollary 3.2. Let assumption (14) in Theorem 3.1 be replaced by
and
Then every solution 

Let 

Corollary 3.3. Let assumption (14) in Theorem 3.1 be replaced by
for some integer


Next we establish conditions for the oscillation of all solutions of (E), (B1) subject to the following con- ditions:
C3)
C4) 


Theorem 3.2. In addition to conditions (C3) and (C4) assume 


and

where
Proof. Suppose that 






Let 



and 

Let 

Integrating the last inequality from 


since 
Letting 

where 

From Lemma 3.2 there are two possible cases for




Integrating the last inequality from 


By (C4) and Lemma 3.3, we have from (32)

Letting 

For this case 





and 

From (34) and (35) we have

which contradicts (27).
Next we consider the case that 



Consider 

Let 
here we have used (C4), (37) and Lemma 3.4. Integrating the last inequality from 

and so letting
which contradicts (28). This completes the proof.
Next we consider (E), (B1) subject to the following conditions:
C5) 


Theorem 3.3. In addition to conditions (C3) and (C5) assume that

and

Then every solution 

Proof. Without loss of generality we may assume that 


If 




which contradicts (38). For this case 

We consider the fractional differential 

Let 
according as 






Integrating and rearranging we obtain
and so letting 
which contradicts (39). This completes the proof.
4. Oscillation of (E), (B2)
In this section we establish sufficient conditions for the oscillation of all solutions of (E), (B2). For this we need the following:
The smallest eigen value 
is positive and the corresponding eigen function 

Theorem 4.1. Let all the conditions of Theorem 3.1 be hold. Then every solution of (E), (B2) oscillates in
Proof. Suppose that 








We obtain for

Using Green’s formula and boundary condition (B2) it follows that

and for

Also from (A3), (A5), we obtain

and using and Jensen’s inequality we get

Set

In view of (41)-(45) and (A6), (40) yield

for 
Using the above theorem, we derive the following Corollaries.
Corollary 4.1. If the inequality (46) has no eventually positive solutions, then every solution 
Corollary 4.2. Let the conditions of Corollary 3.2 hold; then every solution 
Corollary 4.3. Let the conditions of Corollary 3.3 hold; then every solution 
Theorem 4.2. Let the conditions of Theorem 3.2 hold; then every solution 
Theorem 4.3. Let the conditions of Theorem 3.3 hold; then every solution 
The proof Theorems 4.2 and 4.3 are similar to that of Theorem 4.1 and ends details are omitted.
5. Examples
In this section we give some examples to illustrate our results established in Sections 3 and 4.
Example 1. Consider the fractional neutral partial differential equation

for 

Example 1 is particular case of Equation (E). Here
and
It is easy to see that
Here n = 1, m = 1, so we have
Take
Here m = 1, n = 1 so we have
Consider
Choose 

Thus all the conditions of Corollary 3.3 are satisfied. Hence every solution of (E1), (47) oscillates in 

Example 2. Consider the fractional neutral partial differential equation

for 

Here

It is easy to see that
Take
Consider
Choose 

Thus all the conditions of Corollary 3.3 are satisfied. Therefore every solution of (E2), (48) oscillates in

Acknowledgements
The authors thank Prof. E. Thandapani for his support to complete the paper. Also the authors express their sincere thanks to the referee for valuable suggestions.
Cite this paper
V.Sadhasivam,J.Kavitha, (2015) Forced Oscillation of Solutions of a Fractional Neutral Partial Functional Differential Equation. Applied Mathematics,06,1302-1317. doi: 10.4236/am.2015.68124
References
- 1. Miller, K.S. and Ross, B. (1993) An Introduction to the Fractional Calculus and Fractional Differential Equations. John Wiley and Sons, New York.
- 2. Podlubny, I. (1999) Fractional Differential Equations. Academic Press, San Diego.
- 3. Kilbas, A.A., Srivastava, H.M. and Trujillo, J.J. (2006) Theory and Applications of Fractional Differential Equations, Volume 204. Elsevier Science B.V., Amsterdam.
- 4. Das, S. (2008) Functional Fractional Calculus for System Identification and Controls. Springer, Berlin.
- 5. Zhou, Y. (2014) Basic Theory of Fractional Differential Equations. World Scientific, Singapore.
http://dx.doi.org/10.1142/9069 - 6. Wu, J. (1996) Theory of Partial Functional Differential Equations Applications. Springer, New York.
http://dx.doi.org/10.1007/978-1-4612-4050-1 - 7. Thandapani, E. and Savithri, R. (2003) On Oscillation of a Neutral Partial Functional Differential Equation. Bulletin of the Institute of Mathematics - Academia Sinica, 31, 273-292.
- 8. Xu, R. and Meng, F. (2013) Oscillation Criteria for Neutral Partial Functional Differential Equations. Differential Equations & Applications, 5, 69-82.
http://dx.doi.org/10.7153/dea-05-05 - 9. Lakshimikantham, V. and Vasundhara Devi, J. (2008) Theory of Fractional Differential Equations in a Banach Space. European Journal of Pure and Applied Mathematics, 1, 38-45.
- 10. Chen, D.X. (2012) Oscillation criteria of Fractional Differential Equations. Advances in Difference Equations, 33.
http://dx.doi.org/10.1186/1687-1847-2012-33 - 11. Grace, S.R., Agarwal, R.P., Wong, P.J.Y. and Zaffer, A. (2012) On the Oscillation of Fractional Differential Equations. Fractional Calculus and Applied Analysis, 15, 222-231.
http://dx.doi.org/10.2478/s13540-012-0016-1 - 12. Chen, D.X. (2013) Oscillatory Behavior of a Class of Fractional Differential Equations with Damping. U.P.B. Sci. Bull., Series A, 75, 107-118.
- 13. Feng, Q.H. and Meng, F.W. (2013) Oscillation of Solutions to Nonlinear Forced Fractional Differential Equation. Electronic Journal of Differential Equations, 2013, 1-10.
- 14. Zheng, B. (2013) Oscillation for a Class of Nonlinear Fractional Differential Equations with Damping Term. J. Adv. Math. Stud, 6, 107-115.
- 15. Han, Z.L. Zhao, Y.G., Sun, Y. and Zhang, C. (2013) Oscillation for a Class of Fractional Differential Equations. Discrete Dynamics in Nature and Society, 2013, 6 p.
- 16. Prakash, P., Harikrishnan, S., Nieto, J.J. and Kim, J.H. (2014) Oscillation of a Time Fractional Partial Differential Equation. Electronic Journal of Qualitative Theory of Differential Equations, 15, 1-10.
http://dx.doi.org/10.14232/ejqtde.2014.1.15 - 17. Li, W.N. (2015) Forced Oscillation Criteria for a Class of Fractional Partial Differential Equations with Damping Term. Mathematical Problems in Engineering, 2015, Article ID: 410904, 6 p.
NOTES
*Corresponding author.

















































































