Applied Mathematics
Vol.4 No.7(2013), Article ID:34622,3 pages DOI:10.4236/am.2013.47147
 -Labeling Number of the Product and the Join Graph on Two Fans
-Labeling Number of the Product and the Join Graph on Two Fans
School of Mathematical Sciences, University of Jinan, Jinan, China
Email: ss_maql@ujn.edu.cn
Copyright © 2013 Sumei Zhang, Qiaoling Ma. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 18, 2013; revised May 18, 2013; accepted May 25, 2013
Keywords: Labeling Number; Join Graph; Product Graph
ABSTRACT
 -labeling number of the product and the join graph on two fans are discussed in this paper, we proved that
-labeling number of the product and the join graph on two fans are discussed in this paper, we proved that  -labeling number of the product graph on two fans is
-labeling number of the product graph on two fans is ,
,  -labeling number of the join graph on two fans is
-labeling number of the join graph on two fans is .
.
1. Introduction
Throughout this paper, we consider connected graphs without loops or multiple edges. For a graph 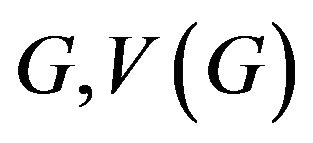 and
and  are used to denote the vertex set and edge set of
are used to denote the vertex set and edge set of  and
and 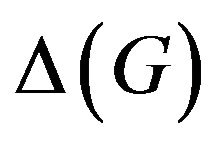 denote the minimum degree and the maximum degree of a graph G, respectively. For a vertex
denote the minimum degree and the maximum degree of a graph G, respectively. For a vertex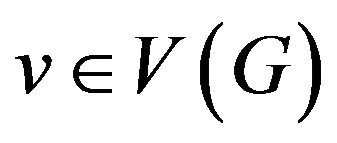 , the neighborhood of v in G is
, the neighborhood of v in G is  is adjacent to v in
is adjacent to v in . Vertices in
. Vertices in  are called neighbors of v,
are called neighbors of v, 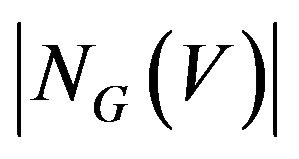 denotes the number of vertices in
denotes the number of vertices in . The other terminology and notations are referred to [1].
. The other terminology and notations are referred to [1].
For a given graph G, an integer , an
, an  - labeling of G is defined as a function
- labeling of G is defined as a function  such that
such that  if
if ; and
; and  if
if , where
, where , the distance of u and v, is the length (number of edges) of a shortest path between u and v. the
, the distance of u and v, is the length (number of edges) of a shortest path between u and v. the  -labeling number, denoted
-labeling number, denoted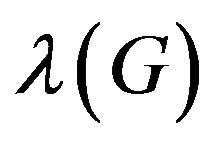 , is the least integer
, is the least integer  such that G has a
such that G has a  -labeling.
-labeling.
The Motivated by the channel assignment problem introduced by Hale in [2], the  labeling have been studied extensively in the past decade. In 1992, in [3] Griggs and Yeh proposed the famous conjecture, for any graph
labeling have been studied extensively in the past decade. In 1992, in [3] Griggs and Yeh proposed the famous conjecture, for any graph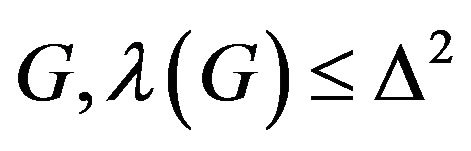 .
.
Griggs and Yeh in [3] proved that the conjecture true fop path, tree, circle, wheel and the graph with diameter 2, G. J. chang and David Kuo in [4] proved that 
 for any graph. Recently Kral D and Skrekovski R in [5] proved the upper is
for any graph. Recently Kral D and Skrekovski R in [5] proved the upper is . It is difficult to prove the conjecture. Now, the study of
. It is difficult to prove the conjecture. Now, the study of  - labeling is focus on special graph. Georges [6,7] give some good results. Zhang and Ma studied the labeling of some special graph, giving some good results in [8-11].
- labeling is focus on special graph. Georges [6,7] give some good results. Zhang and Ma studied the labeling of some special graph, giving some good results in [8-11].
In this paper, we studied the  -labeling number of the product and the join graph on two fans.
-labeling number of the product and the join graph on two fans.
2.  -Labeling Number of the Join Graph on Two Fans
-Labeling Number of the Join Graph on Two Fans
Definition 2.1 Let 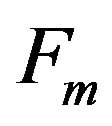 be a fan with m + 1 vertices
be a fan with m + 1 vertices , in which
, in which .
.
Definition 2.2 Let G and H be two graphs, the join of G and H denoted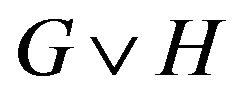 , is a graph obtained by starting with a disjoint union of G and H, and adding edges joining each vertex of G to each vertex of H.
, is a graph obtained by starting with a disjoint union of G and H, and adding edges joining each vertex of G to each vertex of H.
Theorem 2.1 Let , if
, if , then
, then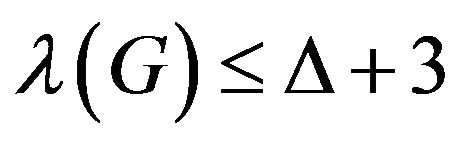 .
.
Proof. In , for arbitrary vertex u and v, such that
, for arbitrary vertex u and v, such that , clearly
, clearly .
.
Let k denote the maximum labeling number of 
First, we give a  -labeling of
-labeling of 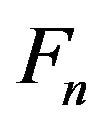 as follows,
as follows, .
.
If 
 when
when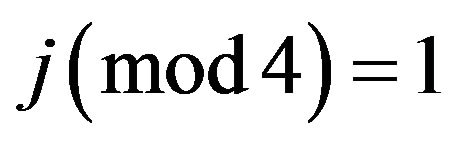 ,
,
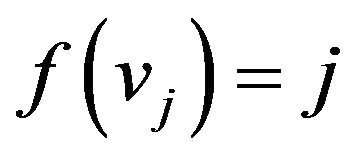 when
when ,
,
 when
when ,
,
 when
when .
.
If , let
, let
 ,
,  ,
,
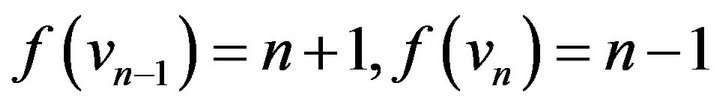 .
.
If , let
, let
 ,
,  ,
,
 .
.
If , let
, let
 ,
,  ,
,
 .
.
If , let
, let
 ,
,
 .
.
Clearly, .
.
Then we label the vertex of  as followsIf
as followsIf 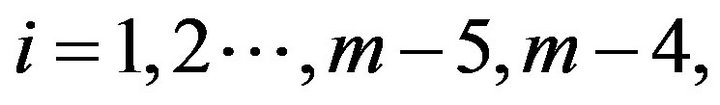
 ,
,
 when
when ,
,
 when
when ,
,
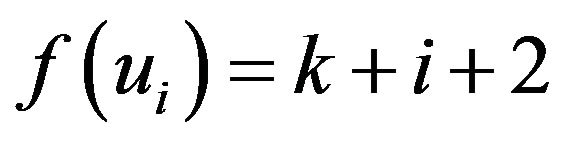 when
when ,
,
 when
when .
.
If , let
, let
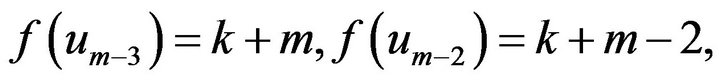

If , let
, let


If , let
, let
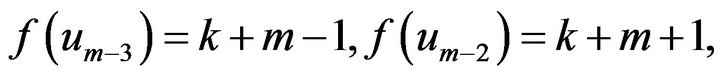

If , let
, let

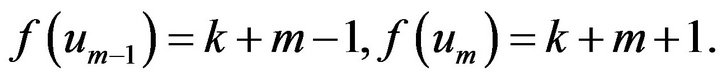
From aboveIf ,
, is the maximum number in
is the maximum number in , and
, and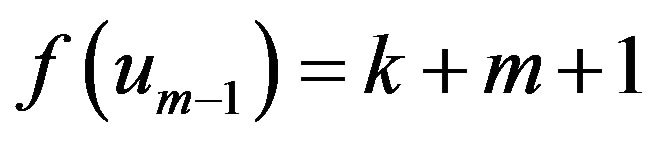 , then
, then
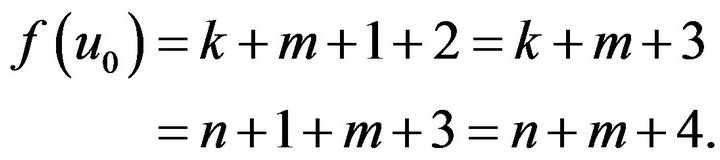
If ,
, is the maximum number in
is the maximum number in , and
, and , then
, then

If ,
, is the maximum number in
is the maximum number in , and
, and , then
, then
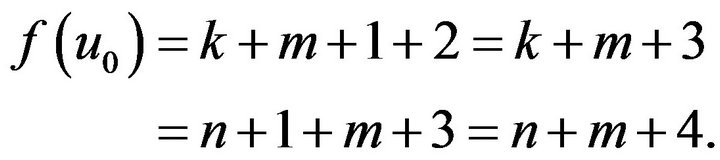
If ,
, is the maximum number in
is the maximum number in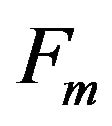 , and
, and , then
, then
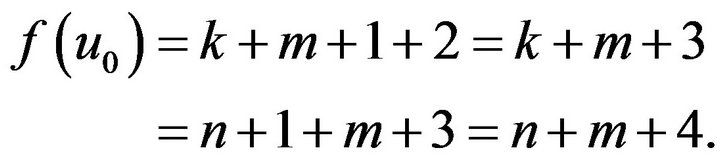
So 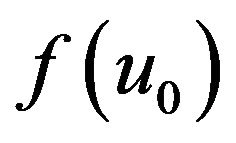 is the maximum number in
is the maximum number in , and
, and , and
, and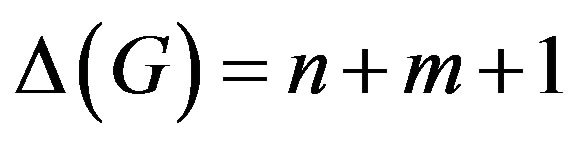 .
.
Obviously, f is a  -
- -labeling of GThen
-labeling of GThen .
.
3.  -Labeling Number of the Product Graph on Two Fans
-Labeling Number of the Product Graph on Two Fans
Definition 3.1 The Cartesian product of graph G and H, denoted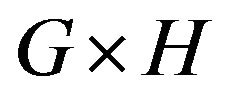 , which vertex set and edge set are the follows:
, which vertex set and edge set are the follows:
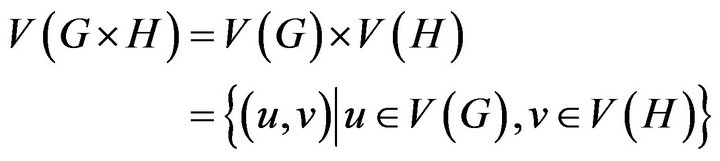

Theorem 3.1 Let , if
, if , then
, then .
.
Proof. In , the other vertices
, the other vertices 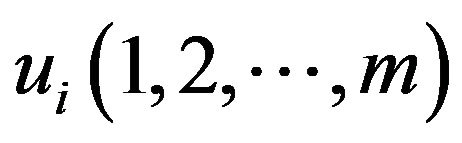 , In
, In , the other vertices
, the other vertices
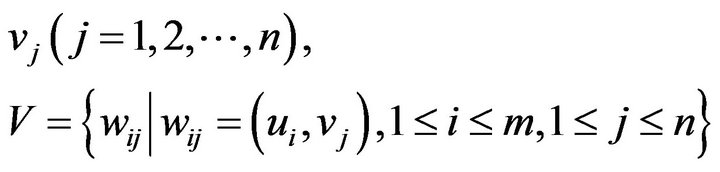
denote the vertex of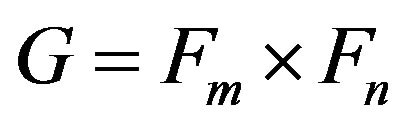 , Obviously,
, Obviously,  , for
, for .
.
We give a  -labeling of G as follows, First, let
-labeling of G as follows, First, let
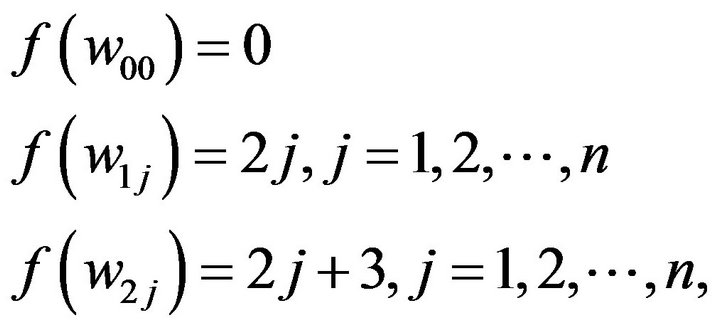
We have the maximum labeling number is 2n + 3.
Then let

From above,  is the maximum labeling number.
is the maximum labeling number.
Finally, let  Obviously,
Obviously, 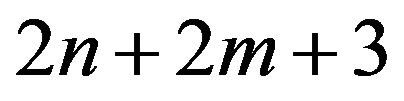 is the maximum labeling number in these
is the maximum labeling number in these  since n ≤ m < 2n, then the maximum labeling number no more than
since n ≤ m < 2n, then the maximum labeling number no more than , and
, and , so
, so .
.
REFERENCES
- J. A. Bondy and U. S. R. Murty, “Graph Theory with Applications,” Macmillan, New York, 1976.
- W. K. Hale, “Frequency Assignment: Theory and Applications,” IEEE Proceedings, Vol. 68, No. 12, 1980, pp. 1497-1514. doi:10.1109/PROC.1980.11899
- J. R. Griggs and R. K. Yeh, “Labeling Graphs with a Condition at Distance 2,” SIAM Journal on Discrete Mathematics, Vol. 5, No. 4, 1992, pp. 586-595. doi:10.1137/0405048
- G. J. Chang and D. Kuo, “The L(2,1)-Labeling Problem on Graphs,” SIAM Journal on Discrete Mathematics, Vol. 9, No. 2, 1996, pp. 309-316. doi:10.1137/S0895480193245339
- D. Král and R. A. Škrekovski, “Theorem about the Channel Asscgnment Problem,” SIAM Journal on Discrete Mathematics, Vol. 16, No. 3, 2003, pp. 426-437. doi:10.1137/S0895480101399449
- J. P. Georges, D. W. Mauro and M. I. Stein, “Labeling Products of Complete Graphs with a Condition at Distance Two,” SIAM Journal on Discrete Mathematics, Vol. 14, No. 1, 2000, pp. 28-35. doi:10.1137/S0895480199351859
- J. P. Georges, D. W. Mauro and M. A. Whittlesey, “Relating Path Covering to Vertex Labelling with a Condition at Distance Two,” Discrete Mathematics, Vol. 135, 1994, pp. 103-111. doi:10.1016/0012-365X(93)E0098-O
- S. M. Zhang and Q. L. Ma, “On List (2,1)-Labelling of Some Planar Graphs,” Ars Combinatoria, Vol. 84, 2007, pp. 231-241.
- S. M. Zhang and Q. L. Ma, “Labelling Some Planar Graphs with a Condition at Distance Two,” Journal of Applied Mathematics and Computing, Vol. 24, No. 1-2, 2007, pp. 421-426.
- S. M. Zhang and J. H. Wang, “L(p,q)-Labeling of Planar Graph with High Maximum Degree,” Journal of Shandong University, Vol. 42, No. 4, 2007, pp. 39-43.
- S. M. Zhang and Q. L. Ma, “L(d,1)-Total Labeling of Outerplannar Graphs,” Journal of Jinnan University, Vol. 20, No. 3, 2006, pp. 258-260.

