ABSTRACT

The harmonic index of a graph is defined as, where denotes the degree of a vertex in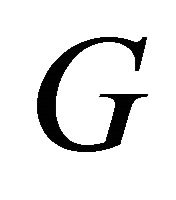. In this work, we give another expression for the Harmonic index. Using this expression, we give the minimum value of the harmonic index for any triangle-free graphs with order and minimum degree for and show the corresponding extremal graph is the complete graph.

1. Introduction

All graphs considered in the following will be simple. Let 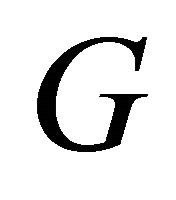be a graph with vertex set and edge set. The order and size of graph are the number of its vertices and number of its edges, respectively. For undefined terminology and notations, we refer the reader to [1].

For a graph, the harmonic index is defined as

It has been found that the harmonic index, which is a special case of general sum-connectivity index, correlates well with the Randić index [2,3] and the -electronic energy of benzenoid hydrocarbons [4,5]. In [6], Favaron et al. considered the relation between harmonic index and the eigenvalues of graphs. Zhong [7] found the minimum and maximum values of the harmonic index for connected graphs and trees, and characterized the corresponding extremal graphs. Recently, Wu et al. [8] give a best possible lower bound for the harmonic index of a graph (a triangle-free graph, respectively) with order and minimum degree at least two and characterize the extremal graphs. In this work, we will give a best possible lower bound for the harmonic index of a triangle-free graph with order and minimum degree at least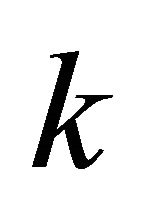. We show the corresponding extremal graph is the complete bipartite graph.

2. Another Expression for the Harmonic Index

Before we go forwards to investigate the relationship between the Harmonic index and the minimum degree of triangle-free graphs, we will give another expression for the Harmonic index in this section, which is vital in sequel.

Let be a graphs with order and minimum degree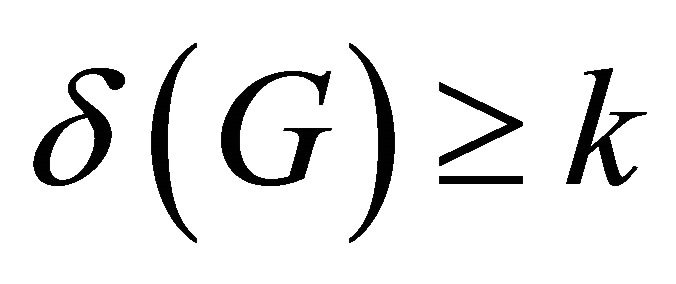. Denote by , the number of edges joining the vertices of degrees and. Denote by the number of vertices of degree of. Then

(1)

(2)

By counting the edges that incident to a vertex of degree, , one obtains

(3)

Substituting Equation (3) back into Equation (2) and performing appropriate rearrangements, we get

(4)

Now, rewriting Equation (1) as

(5)

and combining Equations (4) and (5) so as to eliminate the term, we arrive at

i.e.,

(6)

(7)

Remark 2.1 From (7), we see that for

vertex graph and the equality holds if and only if 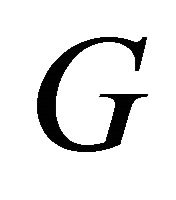is regular.

3. Main Results

First, we give a lower bound for any triangle-free graph with order and size.

Lemma 3.1 For any triangle-free graph with order and size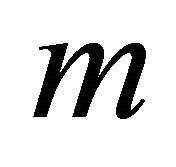, then

where equality holds if and only if is of the form for some natural numbers, and

.

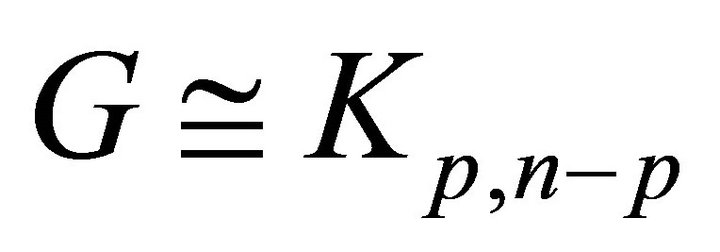Proof. For any edge of, we have , or it would contain triangle(s). By (1), we have

equality holds if and only if for every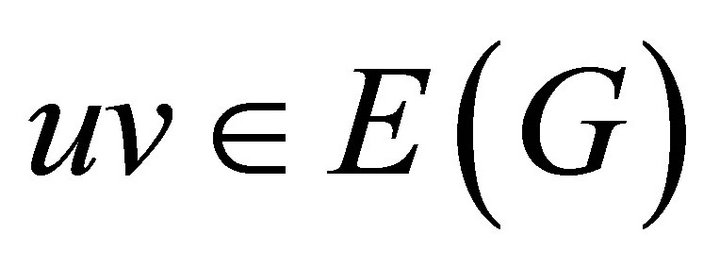. Thus, if we denote for an edge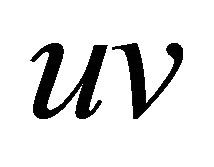, then each of the neighbors, including, of should has degree. Similarly, each of the neighbors of 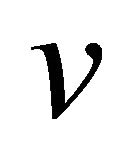has degree. Therefore, 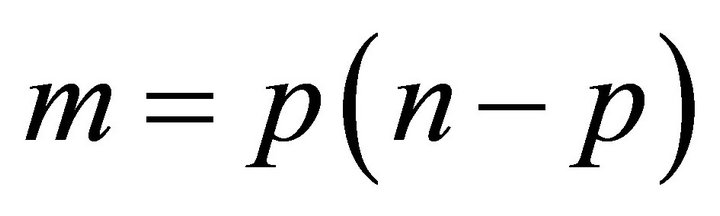and.

Lemma 3.2 Let, forthen is decreasing in and increasing in.

Proof. We have

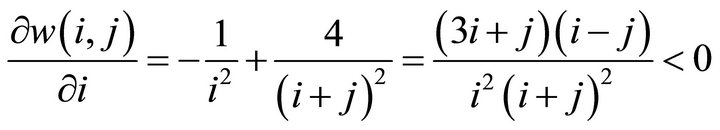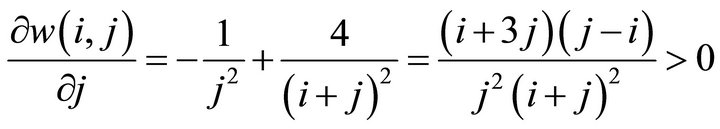and for .

Theorem 3.3 Let be a triangle-free graph with order 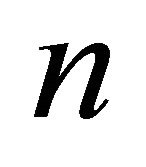and the minimum degree 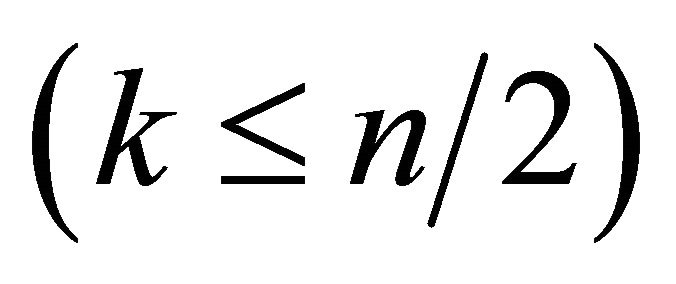. Then

where equality holds if and only if.

Proof. Assume is the size of graph. We divide the proof into the following two cases.

Case 1.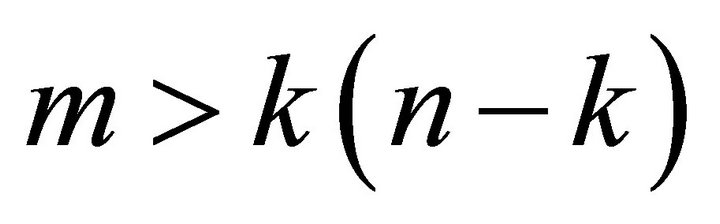. The result follows by Lemma 3.1.

Case 2.. Note that the maximum degree for graph, or it would contain triangle(s). By (6) and Lemma 3.2, we have

For equalities to hold above, we must have 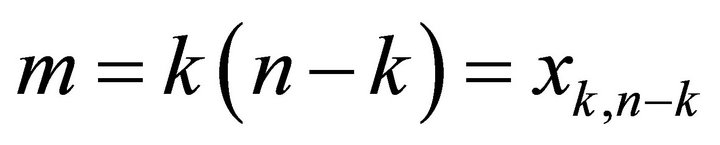, which means that.

REFERENCES

NOTES

^*Research supported by the National Natural Science Foundation of China (No.11101097) and Foundation for Distinguished Young Talents in Higher Education of Guangdong, China (No.LYM11061).