Received 12 August 2014; revised 12 September 2014; accepted 19 September 2014

ABSTRACT

In this paper, we introduce the concept of dual quermassintegral differences. Further, we give the dual Brunn-Minkowski inequality and dual Minkowski inequality for dual quermassintegral differences for mixed intersection bodies.

Keywords:

Intersection Body, Dual Brunn-Minkowski Inequality, Dual Minkowski Inequality

1. Introduction

The projection body was introduced in 1934 by Minkowski [1] . The research on the projection body has attracted much attention. The intersection operator and the class of intersection bodies were introduced in 1988 by Lutwak [2] , who found a close connection between those bodies and famous Busemann-Petty problem (See [3] - [6] ).

In [2] , Lutwak presented the mysterious duality between projection and intersection bodies.

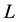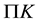For convex bodies K and, let and 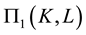denote the projection body of K and mixed projection body of K and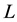, respectively. In [7] , Lutwak established the following Brunn-Minkowski inequality for projection body and Minkowski inequality for mixed projection body:

Theorem A. Let K and 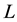be convex bodies in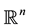. Then

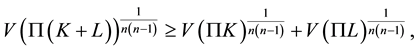(1.1)

with equality if and only if K and 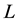are homothetic.

Theorem B. Let K and 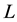be convex bodies in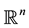. Then

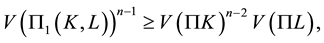(1.2)

with equality if and only if K and 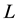are homothetic.

In [8] , Theorem A and Theorem B were extended to volume differences:

Theorem C. Suppose that K, L, and 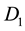are convex bodies in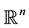, and, , is a homo- thetic copy of. Then

(1.3)

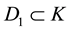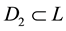with equality if and only if K and are homothetic and, where is a constant.

Theorem D. Suppose that, and are convex bodies in, and, , is a ho- mothetic copy of. Then

(1.4)

with equality if and only if K and L are homothetic.

For star bodies K and, let and denote the intersection body of K and mixed intersection body of K and, respectively. In [9] , Zhao et al. established the following dual Brunn-Minkowski inequality for intersection body and dual Minkowski inequality for mixed intersection body:

Theorem E. Let K and be star bodies in. Then

(1.5)

with equality if and only if is a dilatate of K.

Theorem F. Let K and be star bodies in. Then

(1.6)

with equality if and only if is a dilatate of K.

In this paper, we shall prove the dual forms of inequalities (1.3) and (1.4) for mixed intersection body. In this work new contributions that illustrate this mysterious duality will be presented. Our main results can be stated as follows:

Theorem 1.1. Let and are star bodies in and, is a dilatation of. Then

(1.7)

with equality if and only if is a dilatate of K and, where is a constant.

Theorem 1.2. Let and are star bodies in and, is a dilatation of. Then

(1.8)

with equality if and only if is a dilatate of K.

Please see the next section for related definitions and notations.

2. Definitions and Notations

In this section, we will recall some basic results for dual quermassintegrals of star bodies. The reader is referred to Gardner [10] , Lutwak [2] [11] and Thompson [12] for the Brunn-Minkowski theory with its dual theory.

As usual, let denote the unit ball in Euclidean -space,. While its boundary is and its volume is denoted by. For a compact subset K of, with, star-shaped with respect to, the radial function, is defined by

(2.1)

If is continuous and positive, K will be called a star body.

Two star bodies are said to be dilatate (of each other) if is independent of.

The radial sum of two star bodies is defined as the star body K satisfying. This operation will be denoted by, i.e.,

For star bodies, the dual mixed volume is defined by (see e.g. [11] )

(2.2)

If, and, then the dual mixed volume is called dual -quermassintegral of, and denoted by and allow. It is easily seen that.

Let and be star bodies in. If, then the dual -quermassintegral difference function of and, , can be defined by

(2.3)

If in (2.3), then we get the volume difference of star bodies and:

(See [13] for the concept of the volume difference of two compact domains).

The intersection body of a star body K, , is the centrally symmetric body whose radial function on is given by [2]

(2.4)

where is -dimensional volume.

Let be star bodies in. The mixed intersection body of star bodies is defined by

(2.5)

where is -dimensional dual mixed volume.

If, , then will be denoted as. If, then is called the intersection body of order of; it will often be written as. Specially,. This term was introduced by Zhang [14] .

3. Inequalities for Dual Quermassintegral Differences

In this section, we will establish two inequalities for dual quermassintegral differences of star bodies, which are generalizations of Theorem 1.1 and Theorem 1.2 presented in introduction.

Theorem 3.1. Suppose that and are star bodies in, is a dilatate of. If, , then

with equality if and only if is a dilatate of K and where is a constant.

Obviously, the case in Theorem 3.1 is just Theorem 1.1. Furthermore, taking and to be two closed balls with radii and in Theorem 1.1, we infer

Corollary 3.2. Let and be the circumradii of star bodies K and L. If, , then

with equality if and only if is a dilatate of K and.

Theorem 3.3. Suppose that and D₁ are star bodies in, D₂ is a dilatate of D₁. If, and. Then

with equality if and only if is a dilatate of K and where is a constant.

Obviously, the case in Theorem 3.3 is just Theorem 1.2.

We will require some additional notations and two analytic inequalities to prove Theorem 3.1 and Theorem 3.3. Firstly, we define a function by

where for p > 0. Note that is an indefinite form of its variables.

Lemma 3.4. If, , then, and

(3.1)

with equality holds if and only if the coordinates of are proportional.

A proof of Lemma 3.4 can be found in [15] . The inequality (3.1) was first proved by Bellman [16] and is known as Bellman’s inequality.

Lemma 3.5. If, and. Let and, then

with equality if and only if.

Proof. Consider the following function

Let

We get.

On the other hand, if, then; if then, and it follows that

This completes the proof.

Lemma 3.6. [15] Let be star bodies in. If, then

(3.2)

and

(3.3)

with equality if and only if is a dilatate of.

Proof of Theorem 3.1. For star bodies, applying inequality (3.2), we have

(3.4)

with equality if and only if is a dilatate of.

(3.5)

Since, we get

From (3.4) and (3.5), we obtain that

Then by Lemma 3.4, we get

(3.6)

Note that the equality holds in (3.4) if and only if L is a dilatate of K. By Lemma 3.4 we know that the equality holds in (3.6) if and only if L is a dilatate of K. and is proportional to

This completes the proof.

Proof of Theorem 3.3. Applying inequality (3.3), we have

with equality if and only if is a dilatate of.

Hence, by Lemma 3.5, we obtain that

The proof is complete.

Acknowledgments

We thank the Editor and the referee for their comments. The research is supported by National Natural Science Foundation of China (11101216), Qing Lan Project and the Nanjing Xiaozhuang University (2010KYQN24, 2010KYYB13).

References

NOTES

^*Corresponding author.