Theoretical Economics Letters
Vol.4 No.7(2014), Article ID:48214,4 pages
DOI:10.4236/tel.2014.47064
A Note on Dynamic Roy’s Identity
Libo Xu1, Kam Yu2
1Department of Economics, University of Calgary, Calgary, Canada
2Department of Economics, Lakehead University, Thunder Bay, Canada
Email: libxu@ucalgary.ca, kam.yu@lakeheadu.ca
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 May 2014; revised 26 June 2014; accepted 25 July 2014
ABSTRACT
We derive two forms of Roy’s identity for a dynamic consumption model. The results are potentially useful in theoretical and empirical studies.
Keywords: Roy’s Identity, Inter-Temporal Consumption

1. Introduction
Roy’s identity is a useful tool in theoretical and empirical studies of static consumption problems. Most dynamic consumer problems, however, concentrate on obtaining the optimal consumption path derived from the Euler equation. In this note we assume that the consumer makes decision in a two-stage process. In the dynamic stage, two forms of Roy’s identity are derived. The first form relates the asset holding in each period to the marginal utility of interest rate and the marginal utility of income. The second form resembles the classic Roy’s identity in the static analysis.
2. Dynamic Roy’s Identity
The consumer is supposed to be making a two-stage decision. In the first stage, an inter-temporal decision on aggregate consumption and saving is made. Abstract from uncertainty about the future, a simple model of the decision problem can be set up as
 (1)
(1)
subject to the budget constraints
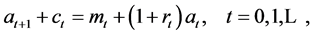 (2)
(2)
where ,
,
 , and
, and
 are exogenous asset, income, and interest rate respectively in period
are exogenous asset, income, and interest rate respectively in period , with
, with . The choice variables are
. The choice variables are
 and
and . Utility is modelled by a stationary and separable discounted
sum of utility function
. Utility is modelled by a stationary and separable discounted
sum of utility function
 in each period1. The Lagrangian is
in each period1. The Lagrangian is
 (3)
(3)
The first-order conditions are
 (4)
(4)
and the budget constraint (2).
The optimal solution is characterized by the Euler equation
 (5)
(5)
and the consumption function (in the case of constant interest rate)
 (6)
(6)
which implies that in the steady state consumption in each period is a fixed portion
of total wealth. The indirect utility function
 is obtained by substituting
is obtained by substituting
 in (6) into the objective function in (1).
in (6) into the objective function in (1).
In the second stage, the consumer makes decisions on how much to buy in
 number of goods and services in the market given the market prices
number of goods and services in the market given the market prices
 and the aggregate consumption
and the aggregate consumption
 in each period
in each period . The model becomes the standard consumer
optimization problem in microeconomics, that is,
. The model becomes the standard consumer
optimization problem in microeconomics, that is,
 (7)
(7)
subject to

The indirect utility function in each period
 is then
is then

Roy’s identity relates the optimal consumption of each good or service to the marginal disutility of price and the marginal utility of income, that is,

for every good
 in every period
in every period . In other words, consumption of each good
depends on the consumer’s preference structure and the relative price of the good
to other goods and services.
. In other words, consumption of each good
depends on the consumer’s preference structure and the relative price of the good
to other goods and services.
Can we have Roy’s identity for the inter-temporal consumption problem in the first stage? Apply the envelop theorem to (3), we have

Substituting the first-order condition (4) into the above gives
 (8)
(8)
Similarly,
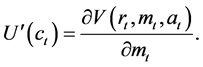 (9)
(9)
Combining (8) and (9) gives the Roy’s identity for the inter-temporal consumption problem as

It says that in any period if the consumer is in debt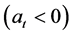 , the marginal utility of an interest rate
increase is negative.
, the marginal utility of an interest rate
increase is negative.
A Roy’s identity similar to the static form can be obtained by considering the “cake-eating”
problem by assuming that income
 in the budget constraint (2) in each period is zero. Then the inter-temporal budget
constraint is reduced to
in the budget constraint (2) in each period is zero. Then the inter-temporal budget
constraint is reduced to

If we define

then the intertemporal utility maximization problem becomes


Notice that
 since
since . Starting in Period 1, price of consumption is decreasing
over time due to discounting. The indirect utility function can be expressed as
. Starting in Period 1, price of consumption is decreasing
over time due to discounting. The indirect utility function can be expressed as

Roy’s identity, in this case, is

3. Conclusion
We have used the envelop theorem to derive two forms of Roy’s identity under an infinite horizontal consumption setting. In the first form, asset holding is related to the marginal utility of interest rate and marginal utility of income. The result can be used as a structural restriction on empirical analysis of inter-temporal consumption. In the second form prices are interpreted as future discount factors. The resulting form resembles the static Roy’s identity.
References
- Carter, M. (2001) Foundations of Mathematical Economics. The MIT Press, Cambridge.
- Wickens, M. (2011) Macroeconomic Theory: A Dynamic General Equilibrium Approach. 2nd Edition, Princeton University Press, Princeton.
NOTES

1See, for example, .

