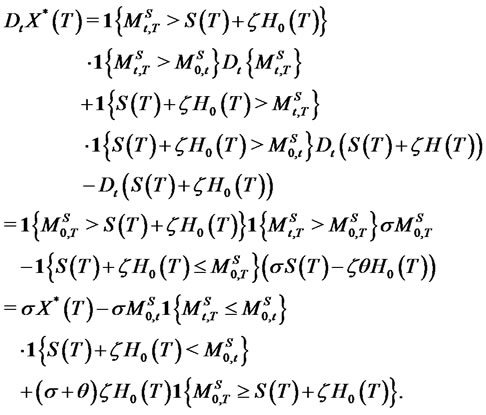Journal of Mathematical Finance
Vol.2 No.3(2012), Article ID:22099,11 pages DOI:10.4236/jmf.2012.23023
Partial Hedging Using Malliavin Calculus
1Department of Management Sciences, Rider University, Lawrenceville, USA
2Department of Statistics and Operations Research, New York University, New York, USA
Email: lnygren@rider.edu, plakner@stern.nyu.edu
Received May 16, 2012; revised June 18, 2012; accepted June 27, 2012
Keywords: Partial Hedging; Malliavin Calculus; Convex Duality; Convex Risk Measure
ABSTRACT
Under the constraint that the initial capital is not enough for a perfect hedge, the problem of deriving an optimal partial hedging portfolio so as to minimize the shortfall risk is worked out by solving two connected subproblems sequentially. One subproblem is to find the optimal terminal wealth that minimizes the shortfall risk. The shortfall risk is quantified by a general convex risk measure to accommodate different levels of risk tolerance. A convex duality approach is used to obtain an explicit formula for the optimal terminal wealth. The second subproblem is to derive the explicit expression for the admissible replicating portfolio that generates the optimal terminal wealth. We show by examples that to solve the second subproblem, the Malliavin calculus approach outperforms the traditional delta-hedging approach even for the simplest claim. Explicit worked-out examples include a European call option and a standard lookback put option.
1. Introduction
A replicating (self-financing) portfolio  designed to eliminate the risk exposure of the target contingent claim completely is called a perfect hedge. Since the value of a perfect hedging portfolio achieves exact replication of the payoff of the target security at the expiration date T, one can offset the risk of the target claim by selling the replicating strategy. In a financial market that is complete and arbitrage free, a perfect hedging strategy exists for any contingent claim with a sufficiently integral terminal payoff
designed to eliminate the risk exposure of the target contingent claim completely is called a perfect hedge. Since the value of a perfect hedging portfolio achieves exact replication of the payoff of the target security at the expiration date T, one can offset the risk of the target claim by selling the replicating strategy. In a financial market that is complete and arbitrage free, a perfect hedging strategy exists for any contingent claim with a sufficiently integral terminal payoff . The cost of replication
. The cost of replication 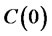 is given by the expected value of the discounted payoff under the unique, risk neutral equivalent martingale measure
is given by the expected value of the discounted payoff under the unique, risk neutral equivalent martingale measure , i.e.,
, i.e.,
 (1)
(1)
where  is the price of the risk-free asset.
is the price of the risk-free asset.
One of the drawbacks of a perfect hedge is that the initial cost of the exact replication (i.e., 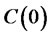 in (1)) is high. In addition, avoiding risks completely means losing out on the potential gain that accepting the risk may have allowed. To this end, we discuss the position of an agent who is unwilling to commit at time
in (1)) is high. In addition, avoiding risks completely means losing out on the potential gain that accepting the risk may have allowed. To this end, we discuss the position of an agent who is unwilling to commit at time  the entire amount
the entire amount  necessary for implementing a perfect hedge and is thus interested in a partial hedging strategy that offers the balance between the cost and the risk exposure. Our goal is to derive optimal partial hedging strategies for various target contingent claims.
necessary for implementing a perfect hedge and is thus interested in a partial hedging strategy that offers the balance between the cost and the risk exposure. Our goal is to derive optimal partial hedging strategies for various target contingent claims.
Since the shortfall risk is intrinsic in a partial hedging environment, one natural way to find the optimal partial hedging strategy would be to minimize the shortfall risk under the constraint that the initial capital  is less than
is less than  (i.e., the amount required for a perfect hedge). The criterion used to quantify the shortfall risk is the expectation of the shortfall
(i.e., the amount required for a perfect hedge). The criterion used to quantify the shortfall risk is the expectation of the shortfall  weighed by a convex loss function g, where
weighed by a convex loss function g, where  is the terminal payoff of a target contingent claim and
is the terminal payoff of a target contingent claim and 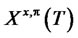 is the value of the hedging portfolio. Compared with the linear loss function criterion adopted by [1] and [2], convexity of the loss function g offers the flexibility to accommodate different types of market participants with different levels of risk tolerance. For example, pension funds and foundations are usually risk-averse whereas hedge funds are more likely to have risk-seeking behaveiors. Moreover, individual investors’ attitudes towards risk are unique depending on their own personal and financial circumstances.
is the value of the hedging portfolio. Compared with the linear loss function criterion adopted by [1] and [2], convexity of the loss function g offers the flexibility to accommodate different types of market participants with different levels of risk tolerance. For example, pension funds and foundations are usually risk-averse whereas hedge funds are more likely to have risk-seeking behaveiors. Moreover, individual investors’ attitudes towards risk are unique depending on their own personal and financial circumstances.
The problem of solving for an optimal partial hedging portfolio so as to minimize the shortfall risk is decomposed into two subproblems. One subproblem is to find the attainable terminal wealth that minimizes the shortfall risk under the insufficient initial capital constraint. A convex duality approach is used to obtain an explicit formula for the optimal terminal wealth . We are the first to use the convex duality approach to study this problem in a systematic way for a general convex loss function. A similar problem was solved in [3] applying the Neyman Pearson lemma. The second subproblem is to derive the explicit expression for the admissible replicating portfolio that generates the optimal terminal wealth
. We are the first to use the convex duality approach to study this problem in a systematic way for a general convex loss function. A similar problem was solved in [3] applying the Neyman Pearson lemma. The second subproblem is to derive the explicit expression for the admissible replicating portfolio that generates the optimal terminal wealth . There are two different approaches to solving the second subproblem. One is the well-known delta-hedging approach and the other is the Malliavin calculus approach. [4] compared these two approaches in the Black and Scholes environment. The author commented that the difficulty of applying the delta-hedging approach is to verify the continuous differentiability condition of the price process of the target claim. In the case of perfect hedge, the difficulty noted above does not exist for a standard call option. The Malliavin calculus approach is only needed for certain path dependent options such as lookback options. However, this is no longer the case in the partial hedging environment. We find that to derive an optimal partial hedging portfolio even for the simplest claim such as an ordinary call option, it is not trivial to verify the continuous differentiability condition for the price process of the optimal terminal wealth. Nevertheless the machinery of the Malliavin calculus approach help circumvent this difficulty. Although the full range of cases remain to be investigated, we illustrate by examples that in the context of partial hedging, the Malliavin calculus approach is not only mathematically rigorous, but also straightforward and easy to implement. Explicit worked-out examples in previous partial hedging studies are only restricted to standard European options. In this paper, by applying the Malliavin calculus approach, we are able to obtain the explicit partial hedging formula for a lookback option.
. There are two different approaches to solving the second subproblem. One is the well-known delta-hedging approach and the other is the Malliavin calculus approach. [4] compared these two approaches in the Black and Scholes environment. The author commented that the difficulty of applying the delta-hedging approach is to verify the continuous differentiability condition of the price process of the target claim. In the case of perfect hedge, the difficulty noted above does not exist for a standard call option. The Malliavin calculus approach is only needed for certain path dependent options such as lookback options. However, this is no longer the case in the partial hedging environment. We find that to derive an optimal partial hedging portfolio even for the simplest claim such as an ordinary call option, it is not trivial to verify the continuous differentiability condition for the price process of the optimal terminal wealth. Nevertheless the machinery of the Malliavin calculus approach help circumvent this difficulty. Although the full range of cases remain to be investigated, we illustrate by examples that in the context of partial hedging, the Malliavin calculus approach is not only mathematically rigorous, but also straightforward and easy to implement. Explicit worked-out examples in previous partial hedging studies are only restricted to standard European options. In this paper, by applying the Malliavin calculus approach, we are able to obtain the explicit partial hedging formula for a lookback option.
It is worth noting that the Malliavin calculus approach has gained considerable interest since it was first introduced to the portfolio theory literature by [5]. For example, [6] applied the Clark-Ocone formula and the gradient operator in Malliavin calculus to derive an explicit representation for the optimal trading strategy in the case of partial information. The Malliavin calculus approach has also been used to derive perfect hedging strategies for lookback and barrier options (see [7,8]). [9] found the Malliavin calculus approach useful in deriving the hedging portfolios for an expected-utility-maximizing investor whose consumption rate and terminal wealth are subject to downside constraints.
The rest of the paper is organized as follows. Section 2 sets up the model for the financial market, presents the dynamics of the agent’s wealth process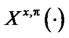 , and defines the class of admissible portfolios
, and defines the class of admissible portfolios . Section 3 solves the problem of minimizing the expected shortfall loss using the convex duality approach. The main result is an explicit expression for the optimal terminal wealth
. Section 3 solves the problem of minimizing the expected shortfall loss using the convex duality approach. The main result is an explicit expression for the optimal terminal wealth . The existence of an optimal hedging strategy is shown as well. The Malliavin calculus approach is summarized in Section 4 and is used to derive the optimal partial hedging portfolios for two specific examples in Section 5.
. The existence of an optimal hedging strategy is shown as well. The Malliavin calculus approach is summarized in Section 4 and is used to derive the optimal partial hedging portfolios for two specific examples in Section 5.
2. The Economy
Since our ultimate interest is to obtain explicit expressions for the optimal partial hedging portfolios, the model under consideration here is a typical Black and Scholes economy as in [10], wherein there are one riskless asset of price 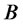 and one risky asset of price
and one risky asset of price . We shall assume that the riskless asset
. We shall assume that the riskless asset  earns a constant instantaneous rate of interest
earns a constant instantaneous rate of interest , and that the price
, and that the price 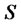 of the risky asset follows a geometric Brownian motion. More specifically, the respective prices
of the risky asset follows a geometric Brownian motion. More specifically, the respective prices  and
and  evolve according to the (stochastic) differential equations
evolve according to the (stochastic) differential equations
 (2)
(2)
 (3)
(3)
All our problems are treated on a finite time-horizon [0,T]. In Equation (3),  is a standard Brownian motion on a complete probability space
is a standard Brownian motion on a complete probability space 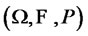 endowed with an augmented filtration
endowed with an augmented filtration 
 generated by the Brownian motion
generated by the Brownian motion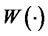 . We assume that
. We assume that  (interest rate),
(interest rate), 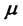 (stock return rate),
(stock return rate), 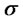 (stock volatility), and
(stock volatility), and  are positive constants.
are positive constants.
Set “the market-price-of-risk” . We introduce the following processes
. We introduce the following processes
 (4)
(4)
 (5)
(5)
and the auxiliary probability measure  defined on
defined on 
 (6)
(6)
According to the Girsanov theorem the process  is a
is a  -Brownian motion on
-Brownian motion on .
.
In the context of the above market model, consider an agent who is endowed with initial wealth , can decide, at each time
, can decide, at each time , which amount
, which amount  to invest in the risky asset without affecting its price. We shall denote by
to invest in the risky asset without affecting its price. We shall denote by  the wealth of this agent at time
the wealth of this agent at time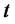 . With
. With  chosen, the investor places the amount
chosen, the investor places the amount  in the bank account. The agent’s wealth process satisfies the equation
in the bank account. The agent’s wealth process satisfies the equation
 (7)
(7)
Formally, we say that a trading strategy  over the time interval
over the time interval 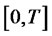 is self-financing if its wealth process satisfies (7). We require that the wealth process
is self-financing if its wealth process satisfies (7). We require that the wealth process  in (7) to be almost surely uniformly bounded from below by zero for the trading strategies
in (7) to be almost surely uniformly bounded from below by zero for the trading strategies  to be admissible. The class of all such admissible trading strategies is denoted by
to be admissible. The class of all such admissible trading strategies is denoted by . Let us introduce the notation
. Let us introduce the notation
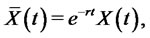 (8)
(8)
the discounted version of the wealth process . We have the equivalent equation
. We have the equivalent equation
 (9)
(9)
We can deduce that the discounted wealth process  is a continuous local martingale under
is a continuous local martingale under . Denoting the process
. Denoting the process
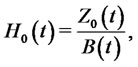 (10)
(10)
with the help of the “Bayes rule”, we can deduce that the process  is a continuous local martingale under
is a continuous local martingale under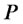 . This process is also bounded from below. An application of Fatou’s lemma shows that
. This process is also bounded from below. An application of Fatou’s lemma shows that 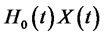 is a supermartingale under
is a supermartingale under . Consequently, we have
. Consequently, we have
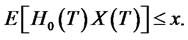 (11)
(11)
Moreover, it is well-known that this market is complete in the following sense: for every initial wealth 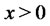 such that
such that  and every nonnegative random variable
and every nonnegative random variable , there exists an admissible trading strategy
, there exists an admissible trading strategy  whose value process satisfies
whose value process satisfies  , P-almost surely.
, P-almost surely.
3. Minimizing the Expected Shortfall Risk
This section is devoted to finding an explicit expression of the optimal terminal wealth that minimizes the expected shortfall risk. Consider a contingent claim whose terminal payoff is given by a  -measurable, nonnegative random variable C. Recall
-measurable, nonnegative random variable C. Recall  defined in (1) and assume
defined in (1) and assume . The value
. The value  is the smallest amount
is the smallest amount  such that there exists an admissible strategy
such that there exists an admissible strategy  whose value process satisfies
whose value process satisfies , P-almost surely (i.e., a perfect hedge). Notice that the notations
, P-almost surely (i.e., a perfect hedge). Notice that the notations  and
and  are interchangeable. In this section, we choose to use the latter to emphasize the value of the portfolio is achieved by a certain amount of initial capital
are interchangeable. In this section, we choose to use the latter to emphasize the value of the portfolio is achieved by a certain amount of initial capital 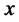 and a specific admissible strategy
and a specific admissible strategy .
.
Now assume that the initial capital  is not enough to do a perfect hedge, i.e.,
is not enough to do a perfect hedge, i.e., . The risk measure used to find the optimal partial hedging strategy takes account of two factors. One is the size of the shortfall
. The risk measure used to find the optimal partial hedging strategy takes account of two factors. One is the size of the shortfall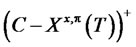 , where
, where . The other is the investor’s attitude towards the shortfall risk, which is captured by a loss function
. The other is the investor’s attitude towards the shortfall risk, which is captured by a loss function . We assume that
. We assume that  is an increasing and strictly convex function defined on
is an increasing and strictly convex function defined on , with
, with . We further assume that
. We further assume that  is in
is in ,
,  , and
, and
 (12)
(12)
We now give the formal definition of the risk measure.
Definition 3.1 The shortfall risk is defined as the expectation
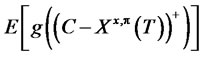 (13)
(13)
of the shortfall weighed by the loss function .
.
Remark 3.1 A special case of the risk measure defined above is the lower partial moment (e.g., [11]) with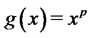 , for some
, for some .
.
Our aim is to find an admissible portfolio 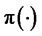 which solves the optimization problem
which solves the optimization problem
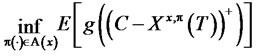 (14)
(14)
for any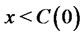 .
.
This stochastic control problem is solved by first finding the optimal terminal wealth  that mini mizes the shortfall risk in (13) under the constraint that
that mini mizes the shortfall risk in (13) under the constraint that . We first make the following useful observation.
. We first make the following useful observation.
Lemma 3.1 Let  such that
such that
 . Then there exists a
. Then there exists a  such that
such that

The proof of the lemma is deferred to the Appendix. In view of Lemma 3.1, we can (and do) assume that  P-almost surely in (14). Hence the risk measure can be written as
P-almost surely in (14). Hence the risk measure can be written as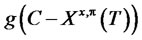 . As noted earlier,
. As noted earlier, 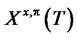 is assumed to be nonnegative. Hence for any admissible portfolio strategy
is assumed to be nonnegative. Hence for any admissible portfolio strategy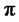 , we have
, we have . Define
. Define  as the inverse of
as the inverse of . In the case of
. In the case of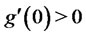 , we can extend the domain of
, we can extend the domain of  to
to  by letting
by letting 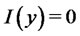 for
for . We shall adopt useful tools from convex duality: starting with the function
. We shall adopt useful tools from convex duality: starting with the function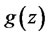 , consider its (random,
, consider its (random,  -measurable) Legendre transform
-measurable) Legendre transform
 (15)
(15)
 (16)
(16)
The supremum is attained by
 (17)
(17)
For the convenience of the reader, we summarize below some basic properties of the function .
.
Lemma 3.2 The function 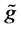 enjoys the following properties.
enjoys the following properties.
1)  for all
for all .
.  is nondecreasing on
is nondecreasing on .
.
2) The function  is convex and continuous.
is convex and continuous.
Proof. a) It follows from the explicit expression of  in (16) that
in (16) that  is nondecreasing. From the facts that
is nondecreasing. From the facts that  is nondecreasing and
is nondecreasing and 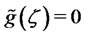 for
for , it is easy to see that
, it is easy to see that 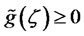 for all
for all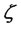 .
.
b) We see immediately from (15) that  is a convex function, since it is the pointwise supremum of a family of convex (indeed, affine) functions of
is a convex function, since it is the pointwise supremum of a family of convex (indeed, affine) functions of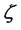 . Note that this is true whether or not
. Note that this is true whether or not  is convex.
is convex.  is continuous on
is continuous on  since a convex function is continuous on an open interval. Continuity of
since a convex function is continuous on an open interval. Continuity of  at
at  follows directly from the explicit expression of
follows directly from the explicit expression of  in (16).
in (16).
It follows that for any initial capital
 , we have
, we have
 (18)
(18)
almost surely. Thus, in conjunction with (6) and (11), we obtain
 (19)
(19)
where we set
 (20)
(20)
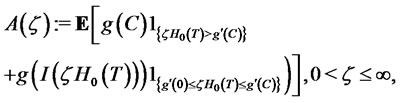 (21)
(21)
Now assume that for every , we have
, we have
 (22)
(22)
Remark 3.2 Note that (22) is not assumed for . So the above assumption still allows
. So the above assumption still allows , which is the case for many popular options.
, which is the case for many popular options.
The function  in (20) possesses the following useful property.
in (20) possesses the following useful property.
Lemma 3.3 Assume that  satisfies (22). The function
satisfies (22). The function  in (20) is continuous on
in (20) is continuous on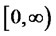 .
.
Proof. First we show that the function

is continuous. Let  be a sequence of non-negative numbers converging to
be a sequence of non-negative numbers converging to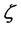 . If
. If , then by assumption (22),
, then by assumption (22),
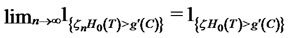 almost surely. Hence
almost surely. Hence  and the dominated convergence theorem implies the continuity of
and the dominated convergence theorem implies the continuity of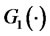 . Assume now that
. Assume now that . Then one can see by separating the cases
. Then one can see by separating the cases  and
and 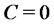 that
that
 almost surely. Another application of the dominated convergence theorem implies that
almost surely. Another application of the dominated convergence theorem implies that  is continuous even at
is continuous even at . The continuity of
. The continuity of

follows similarly using the bound

and the dominated convergence theorem.
To derive the maximum of  in (19), we assume that
in (19), we assume that 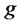 is in
is in  and
and
 (23)
(23)
From (16) it follows that  is convex and continuous on
is convex and continuous on , and continuously differentiable on
, and continuously differentiable on .
.
In particular,
 (24)
(24)
For every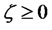 , we have
, we have
 (25)
(25)
Indeed, by assumption (23),
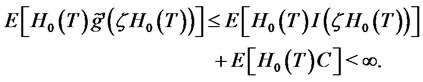 (26)
(26)
We now establish the following auxiliary result.
Lemma 3.4 Define . Then
. Then  is convex on
is convex on , continuously differentiable on
, continuously differentiable on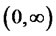 , and
, and
 (27)
(27)
Proof. Convexity of  is inherited from
is inherited from . For any
. For any , let
, let  be an arbitrary positive number such that
be an arbitrary positive number such that  belongs to
belongs to . Then
. Then

as , almost surely, and by the convexity of
, almost surely, and by the convexity of  for
for 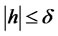

Relation (25) and the dominated convergence theorem imply
 (28)
(28)
The right hand side of (28) is exactly 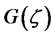 by (24) and (20). We know from Lemma 3.3 that
by (24) and (20). We know from Lemma 3.3 that  is continuous. So
is continuous. So  is indeed continuously differentiable.
is indeed continuously differentiable.
Now we have . The function
. The function  is concave on
is concave on , belongs to
, belongs to , and satisfies
, and satisfies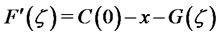 . Note also that
. Note also that
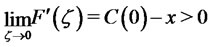
and

So  achieves its maximum over
achieves its maximum over  at
at
 (29)
(29)
Therefore, (19) gives
 (30)
(30)
The following is the crucial observation in the duality approach.
Remark 3.3 (Sufficient and necessary conditions for strong duality) The inequality of (19) holds as equality for some 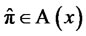 and with
and with , if and only if we have
, if and only if we have
 (31)
(31)
and
 (32)
(32)
Now we are ready to state the main result of this section.
Proposition 3.1 For every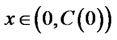 , the value
, the value  is given by (29) and the
is given by (29) and the 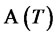 -measurable random variable
-measurable random variable
 (33)
(33)
satisfies
 (34)
(34)
Proof. From (20), (1), and the fact that
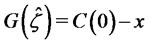 we see that
we see that

Remark 3.4 Notice that whenever , the optimal terminal wealth in (33) has a simple form of
, the optimal terminal wealth in (33) has a simple form of
 . A typical example is the case of lower partial moment with
. A typical example is the case of lower partial moment with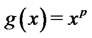 , for some
, for some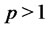 .
.
For the sake of completeness, we include an existence result of the optimal hedging strategy.
Theorem 3.1 Existence of optimal strategy. For any given , and with
, and with  given by (29) and
given by (29) and  given by (33), there exists a portfolio process
given by (33), there exists a portfolio process  for which (31) and (32) hold and which is optimal for the problem of (14):
for which (31) and (32) hold and which is optimal for the problem of (14):
 (35)
(35)
In particular, it is equal to that portfolio which replicates the claim  of (33).
of (33).
Proof. From Proposition 3.1, we can find an  - measurable random variable
- measurable random variable 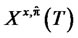 such that (34) holds. Consider now the
such that (34) holds. Consider now the  -martingale (in the notation of (33))
-martingale (in the notation of (33))
 (36)
(36)
written in its representation as a stochastic integral with respect to 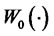 for a suitable portfolio process
for a suitable portfolio process  (see [12], p. 93). The process
(see [12], p. 93). The process  satisfies
satisfies 
 and the requirement that it’s bounded from below by zero, so
and the requirement that it’s bounded from below by zero, so . The optimality of
. The optimality of  is then a consequence of Remark 3.3.
is then a consequence of Remark 3.3.
4. The Malliavin Calculus Approach
To solve the second subproblem of deriving the partial hedging portfolios that generate the optimal terminal wealth in (33), we consider two different approaches. One is the well-known  -hedging approach and the other is the Malliavin calculus approach. For easy reference and to make the paper self-contained, we first briefly recap the concept of
-hedging approach and the other is the Malliavin calculus approach. For easy reference and to make the paper self-contained, we first briefly recap the concept of  -hedging. Then we introduce the definition of the Mallivin derivative of a random variable and the Clark-Ocone formula. Thereafter, we present a Mallivin calculus approach for deriving the replicating portfolio as first used in [5].
-hedging. Then we introduce the definition of the Mallivin derivative of a random variable and the Clark-Ocone formula. Thereafter, we present a Mallivin calculus approach for deriving the replicating portfolio as first used in [5].
In the standard Black and Scholes framework, the  -hedging approach works in the following way. In a complete financial market, the optimal wealth process
-hedging approach works in the following way. In a complete financial market, the optimal wealth process  (The notations
(The notations  and
and  are used interchangeably.) is given by the discounted conditional expectation of the optimal terminal wealth
are used interchangeably.) is given by the discounted conditional expectation of the optimal terminal wealth  under the risk neutral probability measure
under the risk neutral probability measure , i.e.,
, i.e., . In many situations, the optimal wealth process
. In many situations, the optimal wealth process  is a Markov process and is in the form of
is a Markov process and is in the form of , where
, where  is the time t stock price. If the condition that
is the time t stock price. If the condition that 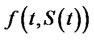 is a
is a  -function is verifiable, we can apply the Itô formula to
-function is verifiable, we can apply the Itô formula to  to obtain
to obtain
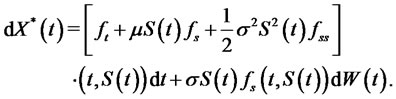 (37)
(37)
The replicating portfolio is denoted by
 where
where  denotes the number of units to be held at time
denotes the number of units to be held at time 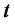 in the risk-free asset
in the risk-free asset , and
, and  denotes the number of units to be held in the stock
denotes the number of units to be held in the stock  at time
at time . Notice the relationship between
. Notice the relationship between  and
and 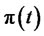 given by
given by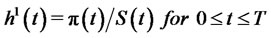 . By the definition of a self-financing portfolio, we have
. By the definition of a self-financing portfolio, we have
 (38)
(38)
From the uniqueness of the Itô integral it follows that we can use (37) and (38) to identify the replicating portfolio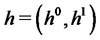 , where
, where
 (39)
(39)
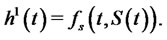 (40)
(40)
Equation (40) is the famous  -hedging formula. As pointed out in [4], the major difficulty of using the
-hedging formula. As pointed out in [4], the major difficulty of using the  -hedging approach is to verifty
-hedging approach is to verifty  satisfies the necessary differentiability condition. We show by examples in the next section how the Malliavin calculus approach can help us get around this difficulty in the partial hedging context.
satisfies the necessary differentiability condition. We show by examples in the next section how the Malliavin calculus approach can help us get around this difficulty in the partial hedging context.
The main components for the Malliavin calculus approach to work are the gradient operator and the ClarkOcone formula. Let  denote the family of all random variables
denote the family of all random variables  of the form
of the form

where  is a polynomial in
is a polynomial in  variables
variables  and
and  for some
for some
 (deterministic). Notice that the set
(deterministic). Notice that the set  is dense in
is dense in . Next, we define the Cameron-Martin space
. Next, we define the Cameron-Martin space  according to
according to

and identify our probability space  with
with

such that  for all
for all . Here
. Here  denotes the Wiener space—the space of all continuous, real-valued functions
denotes the Wiener space—the space of all continuous, real-valued functions  on
on  such that
such that ,
,  denotes the corresponding Borel
denotes the corresponding Borel  -algebra, and
-algebra, and  denotes the unique Wiener measure. With this setup we can define the directional derivative of a random variable
denotes the unique Wiener measure. With this setup we can define the directional derivative of a random variable  in all the directions
in all the directions  by
by
 (41)
(41)
Notice from the above equation that the map  is continuous for all
is continuous for all 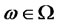 and linear, consequently there exists a stochastic variable
and linear, consequently there exists a stochastic variable  with values in the Cameron-Martin space
with values in the Cameron-Martin space  such that
such that
 .
.
Moreover, since  is an
is an 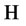 -valued stochastic variable, the map
-valued stochastic variable, the map  is absolutely continuous with respect to the Lebesgue measure on
is absolutely continuous with respect to the Lebesgue measure on . Now we let the Malliavin derivative
. Now we let the Malliavin derivative  denote the Radon-Nikodym derivative of
denote the Radon-Nikodym derivative of 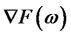 with respect to the Lebesgue measure such that
with respect to the Lebesgue measure such that
 (42)
(42)
If we define this expression with Equation (41) we have the following result, which in many cases is taken directly as a definition.
Definition 4.1 The Malliavin derivative of a stochastic variable  is the stochastic process
is the stochastic process
 given by
given by

We note that the Malliavin derivative is well defined almost everywhere .
.
Let us introduce a norm  on the set
on the set  according to
according to
 (43)
(43)
Now, as the Malliavin derivative is a closable operator (see [13]), we define by  the Banach space which is the closure of
the Banach space which is the closure of  under the norm
under the norm .
.
The Clark-Ocone formula is the cornerstone of the Malliavin calculus hedging approach. This formula is a generalization of the Itô representation theorem (see [14]) in the sense that it gives an explicit expression for the integrand. The original Clark-Ocone formula (see [13]) applies to any  -measurable stochastic variable in the space
-measurable stochastic variable in the space .
.
[8] shows that the Clark-Ocone formula is valid for any  -measurable stochastic variable in
-measurable stochastic variable in  and therefore the Malliavin calculus approach to deriving the replicating portfolio of a contingent claim as in [5] can be extended in a similar way. However, since all of the examples discussed later in the paper only use the Clark-Ocone formula to the stochastic variables in
and therefore the Malliavin calculus approach to deriving the replicating portfolio of a contingent claim as in [5] can be extended in a similar way. However, since all of the examples discussed later in the paper only use the Clark-Ocone formula to the stochastic variables in , we only state the original Clark-Ocone formula in [13] and the results in [5] as a theorem. We refer the interested readers to [8] for the extensions.
, we only state the original Clark-Ocone formula in [13] and the results in [5] as a theorem. We refer the interested readers to [8] for the extensions.
Theorem 4.1 Let the stochastic variable 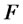 belong to
belong to . Then we have the representation formula
. Then we have the representation formula
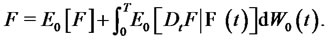
Following the above Clark-Ocone formula and the results in [5], any optimal portfolio 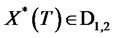 can be replicated by the self-financing portfolio
can be replicated by the self-financing portfolio
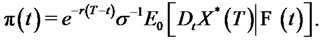 (44)
(44)
In order to derive the replicating portfolio using the above theorem, we need to calculate the Malliavin derivative of . When
. When 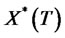 is a Lipschitz function of a stochastic vector process belonging to
is a Lipschitz function of a stochastic vector process belonging to , the following classic chain rule as proved in [13] can be used to calculate
, the following classic chain rule as proved in [13] can be used to calculate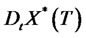 .
.
Proposition 4.1 (Classic Chain Rule in [13]) Let  be a function such that
be a function such that

for any  and some constant K. Suppose that
and some constant K. Suppose that  is a stochastic vector whose components belong to the space
is a stochastic vector whose components belong to the space  and suppose that the law of
and suppose that the law of  is absolutely continuous with respect to the Lebesgue measure on
is absolutely continuous with respect to the Lebesgue measure on . Then
. Then  and
and

5. Derivation of the Replicating Portfolios
In the context of perfect hedging, the  -hedging formula in (40) is the standard method to obtain the replicating portfolio for a European call option (see, e.g., [15], Chapter 5). The reason the
-hedging formula in (40) is the standard method to obtain the replicating portfolio for a European call option (see, e.g., [15], Chapter 5). The reason the  -hedging approach works in this case is that the price of the European call option has a closed-form expression (i.e., the famous Black-Scholes formula) and therefore, it is not hard to verify the required differentiability condition. The first example in this section shows that this is no longer the case in the partial hedging environment. Since the optimal wealth process for partial hedging a standard call option does not possess a closed-form formula, the verification of the continuous differentiability condition is no longer a trivial issue. In the second example, we derive the explicit representation for the partial hedging portfolio of a standard lookback put option. For explicit computational purpose, the loss function we shall use in both examples is
-hedging approach works in this case is that the price of the European call option has a closed-form expression (i.e., the famous Black-Scholes formula) and therefore, it is not hard to verify the required differentiability condition. The first example in this section shows that this is no longer the case in the partial hedging environment. Since the optimal wealth process for partial hedging a standard call option does not possess a closed-form formula, the verification of the continuous differentiability condition is no longer a trivial issue. In the second example, we derive the explicit representation for the partial hedging portfolio of a standard lookback put option. For explicit computational purpose, the loss function we shall use in both examples is , in which case
, in which case . Note that our approach can be straightforwardly adapted to solve the problem with a more general convex loss function.
. Note that our approach can be straightforwardly adapted to solve the problem with a more general convex loss function.
Example 5.1 Consider partial hedging a standard European call option with payoff function
 . It follows from Remark 3.4 and the facts
. It follows from Remark 3.4 and the facts ,
,  that the optimal terminal wealth
that the optimal terminal wealth 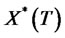 is given by
is given by
 (45)
(45)
From (3), (4), (5), and (10), we have the time T stock price
 (46)
(46)
and the time T state price density
 (47)
(47)
To apply the  -hedging approach, one needs an expression for
-hedging approach, one needs an expression for , which according to (45), is given by
, which according to (45), is given by
 (48)
(48)
From the formulae (3) and (10),  can be written in terms of
can be written in terms of  by
by
 where
where
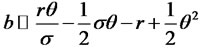 .
.
Let us put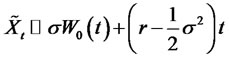 . The expression (48) can be rewritten as
. The expression (48) can be rewritten as
 (49)
(49)
Note that  is independent of
is independent of  and
and  is
is  -measurable. By the basic properties of the Brownian motion, we can rewrite (49) as
-measurable. By the basic properties of the Brownian motion, we can rewrite (49) as
 (50)
(50)
where  is the normal density function with mean
is the normal density function with mean
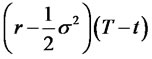 and variance
and variance . To proceed with the
. To proceed with the  -hedging approach, one has to assume that (50) is a
-hedging approach, one has to assume that (50) is a  function of
function of . However, in general, (50) may not have a closed-form expression. Furthermore, notice that the integrand in (50) is not even once differentiable. Therefore, the assumption that (50) is
. However, in general, (50) may not have a closed-form expression. Furthermore, notice that the integrand in (50) is not even once differentiable. Therefore, the assumption that (50) is  seems hard to verify. Nevertheless, for comparison purpose, we ignore this technical difficulty for now and pursue the
seems hard to verify. Nevertheless, for comparison purpose, we ignore this technical difficulty for now and pursue the  -hedging formula. Assuming that the differentiation can be carried out under the integral sign, we obtain
-hedging formula. Assuming that the differentiation can be carried out under the integral sign, we obtain
 (51)
(51)
 (52)
(52)
where the set . Recall the relationship
. Recall the relationship . After further simplifications, we have
. After further simplifications, we have
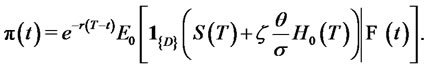 (53)
(53)
We now derive the partial hedging portfolio using the Malliavin calculus approach. The following properties, which are proved in the Appendix, hold.
Corollary 5.1  belongs to
belongs to  and
and

where the set .
.
From Corollary 5.1 and Theorem 4.1, the replicating portfolio is given by
 (54)
(54)
which coincides with the hedging formula in (53). Notice that the Malliavin calculus approach not only avoids the technical difficulty encountered by the  -hedging approach, but also uses much less derivation work.
-hedging approach, but also uses much less derivation work.
Example 5.2 Now let us consider deriving the partial hedging portfolio for a standard lookback put option with terminal payoff 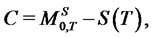 where
where
 . The optimal terminal wealth is given by
. The optimal terminal wealth is given by
 (55)
(55)
To pursue the  -hedging approach, one needs an expression for the optimal wealth process
-hedging approach, one needs an expression for the optimal wealth process
 (56)
(56)
In the Appendix, we show that (56) can be rewritten as
 (57)
(57)
where  and
and  is given in (68). First of all, it is very hard, if not impossible to obtain a closed-form expression for (57). Furthermore, the integrand in (57) is not differentiable with respect to
is given in (68). First of all, it is very hard, if not impossible to obtain a closed-form expression for (57). Furthermore, the integrand in (57) is not differentiable with respect to . Therefore, verification of the differentiability condition is not easy. Even if we ignore this technical difficulty, formal differentiation (disregarding the points where it is non-differentiable) would be possible but gets algebraically very messy in addition to being non-rigorous. For these reasons we abandon the delta-hedging approach and pursue the Malliavin calculus approach instead.
. Therefore, verification of the differentiability condition is not easy. Even if we ignore this technical difficulty, formal differentiation (disregarding the points where it is non-differentiable) would be possible but gets algebraically very messy in addition to being non-rigorous. For these reasons we abandon the delta-hedging approach and pursue the Malliavin calculus approach instead.
Corollary 5.2 Let the optimal terminal wealth be defined by . Then
. Then 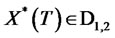 and
and

Proof. See Appendix.
It then follows from Theorem 4.1 and Corollary 5.2 that the replicating portfolio is given by
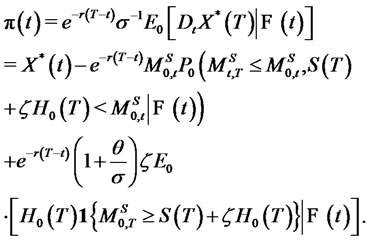 (58)
(58)
Define the Radon-Nikodym derivative

such that  is a probability measure absolutely continuous with respect to
is a probability measure absolutely continuous with respect to . By the Girsanov theorem, the process
. By the Girsanov theorem, the process  is a Brownian motion under the probability measure
is a Brownian motion under the probability measure . Moreover, from Lemma 8.6.2 in [14], it follows that for every stochastic variable
. Moreover, from Lemma 8.6.2 in [14], it follows that for every stochastic variable 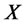 such that
such that ,
,
 (59)
(59)
Now the last conditional expectation on the right hand side of Equation (58) can be written as
 (60)
(60)
Formulae (58) and (60) yield the optimal partial hedging strategy
 (61)
(61)
6. Conclusion
We solved the stochastic control problem of minimizing the expected shortfall risk (quantified by a general convex risk measure) under the constraint that the initial capital is insufficient for a perfect hedge. We showed by examples that the Malliavin calculus approach is useful for finding the replicating portfolios in the partial hedging environment. Further research consists of investigating other target contingent claims and extending the results to incomplete markets.
REFERENCES
- J. Cvitanic and I. Karatzas, “On Dynamic Measures of Risk,” Finance and Stochastics, Vol. 3, No. 4, 1999, pp. 451-482. doi:10.1007/s007800050071
- J. Cvitanic, “Minimizing Expected Loss of Hedging in Incomplete and Constrained Markets,” SIAM Journal on Control and Optimization, Vol. 38, No. 4, 2000, pp. 1050-1066. doi:10.1137/S036301299834185X
- H. Föllmer and P. Leukert, “Efficient Hedging: Cost Versus Shortfall Risk,” Finance and Stochastics, Vol. 4, No. 2, 2000, pp. 117-146. doi:10.1007/s007800050008
- H.-P. Bermin, “Hedging Options: The Malliavin Calculus Approach Versus the
 -Hedging Approach,” Mathematical Finance, Vol. 13, No. 1, 2003, pp. 73-84. doi:10.1111/1467-9965.t01-1-00006
-Hedging Approach,” Mathematical Finance, Vol. 13, No. 1, 2003, pp. 73-84. doi:10.1111/1467-9965.t01-1-00006 - D. Ocone and I. Karatzas, “A Generalized Clark Representation Formula with Applications to Optimal Portfolios,” Stochastics and Stochastic Reports, Vol. 34, No. 3- 4, 1991, pp. 187-220.
- P. Lakner, “Optimal Trading Strategy for an Investor: The Case of Partial Information,” Stochastic Processes and Their Applications, Vol. 76, No. 1, 1998, pp. 77-97. doi:10.1016/S0304-4149(98)00032-5
- H.-P. Bermin, “Hedging Lookback and Partial Lookback Options Using Malliavin Calculus,” Applied Mathematical Finance, Vol. 7, No. 2, 2000, pp. 75-100. doi:10.1080/13504860010014052
- H.-P. Bermin, “A General Approach to Hedging Options: Applications to Barrier and Partial Barrier Options,” Mathematical Finance, Vol. 12, No. 3, 2002, pp. 199-218. doi:10.1111/1467-9965.02007
- P. Lakner and L. M. Nygren, “Portfolio Optimization with Downside Constraints,” Mathematical Finance, Vol. 16, No. 2, 2006, pp. 283-299. doi:10.1111/j.1467-9965.2006.00272.x
- F. Black and M. Scholes, “The Pricing of Options on Corporate Liabilities,” Journal of Political Economy, Vol. 81, No. 3, 1973, pp. 637-659. doi:10.1086/260062
- V. Bawa, “Optimal Rules for Ordering Uncertain Prospects,” Journal of Financial Economics, Vol. 2, No. 1, 1975, pp. 95-121. doi:10.1016/0304-405X(75)90025-2
- I. Karatzas and S. E. Steven, “Methods of Mathematical Finance,” Springer-Verlag, New York, 1998.
- D. Nualart, “The Malliavin Calculus and Related Topics,” Springer-Verlag, Berlin Heidelberg, New York, 1995.
- B. K. Oksendal, “Stochastic Differential Equations: An Introduction with Applications,” 5th Edition, SpringerVerlag, Berlin Heidelberg, New York, 1998.
- M. Musiela and M. Rutkowski, “Martingale Methods in Financial Modelling,” Springer-Verlag, Berlin Heidelberg, 1997.
- R. M. Dudley, “Wiener Functionals as Itô Integrals,” Annals of Probability, Vol. 5, No. 1, 1977, pp. 140-141. doi:10.1214/aop/1176995898
- I. Karatzas and S. E. Shreve, “Brownian Motion and Stochastic Calculus,” Springer-Verlag, New York, 1991. doi:10.1007/978-1-4612-0949-2
Appendix
Proof of Lemma 3.1.
Let  By the market completeness there exists a
By the market completeness there exists a  such that
such that  If
If 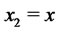 then
then  satisfies the statement of the lemma. Suppose that
satisfies the statement of the lemma. Suppose that . By Dudley’s theorem ([16] or [17], Theorem 3.4.20) there exists a process
. By Dudley’s theorem ([16] or [17], Theorem 3.4.20) there exists a process  satisfying
satisfying

and
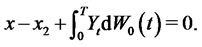
Let

and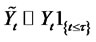 . It follows that
. It follows that
 (62)
(62)
and for every 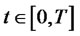
 (63)
(63)
Let . Relations (9), (62), and (63) imply that
. Relations (9), (62), and (63) imply that
 (64)
(64)
Finally we define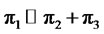 . We have
. We have  since
since

By (64)

Proof of Corollary 5.1. From Corollary 1 in [7], we know that
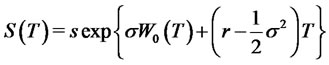
belongs to the Banach space  and
and
 . To show
. To show

and , we approximate
, we approximate  by a sequence in
by a sequence in  and use Definition 4.1 together with the closability of the Malliavin derivative. Notice also that both
and use Definition 4.1 together with the closability of the Malliavin derivative. Notice also that both  and
and 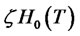 are absolutely continuous. Then
are absolutely continuous. Then  must, as the difference of absolutely continuous functions, be absolutely continuous. Since
must, as the difference of absolutely continuous functions, be absolutely continuous. Since  is a piecewise Lipschitz function for all x, it follows from Proposition 4.1 that
is a piecewise Lipschitz function for all x, it follows from Proposition 4.1 that  with
with

Derivation of Expression (57). We are going to derive an expression for the conditional expectation
 (65)
(65)
Expression (57) can then be obtained by multiplying the above conditional expectation by . Equations (3) and (10) imply the relation
. Equations (3) and (10) imply the relation

Recall the definition for the function
 .
.
Then (65) can be written as
 (66)
(66)
Define the notations  and
and . Then
. Then  can be written as
can be written as . Recall the notation
. Recall the notation
 . In conjunction with the expression
. In conjunction with the expression , for
, for , it follows that
, it follows that . Therefore (66) can be written as
. Therefore (66) can be written as
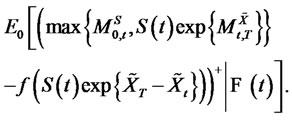 (67)
(67)
We note that  and
and  are independent of
are independent of , whereas
, whereas  and
and  are
are  -measurable. By the well-known properties of the Brownian motion, the joint distribution of
-measurable. By the well-known properties of the Brownian motion, the joint distribution of  coincides with that of
coincides with that of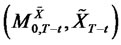 . It is known (see [15], Corollary B.3.1, p. 469) that
. It is known (see [15], Corollary B.3.1, p. 469) that
 (68)
(68)
for  such that
such that  and
and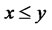 . We can now write (67) as
. We can now write (67) as
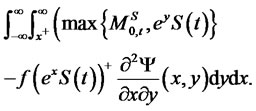 (69)
(69)
The expression (57) is obtained by multiplying (69) by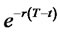 .
.
Proof of Corollary 5.2. Write  as
as

where . From Corollary 1 in [7] and Corollary 5.1 above,
. From Corollary 1 in [7] and Corollary 5.1 above,  ,
,  , and
, and  all belong to
all belong to . Now as
. Now as  is a Lipschitz function for all x, y, and z, we have by Proposition 4.1 that
is a Lipschitz function for all x, y, and z, we have by Proposition 4.1 that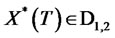 ,and as the joint law of
,and as the joint law of
 is absolutely continuous with respect to the Lebesgue measure on
is absolutely continuous with respect to the Lebesgue measure on 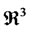 we get that
we get that