Integrability of Hamiltonian Systems with Two Degrees of Freedom and Homogenous Potential of Degree Zero

Jaume Llibre¹, Claudia Valls²

¹Departament de Matemàtiques, Universitat Autònoma de Barcelona, Barcelona, Spain.
²Departamento de Matemática, Instituto Superior Técnico, Universidade de Lisboa, Lisboa, Portugal.

DOI: 10.4236/jamp.2018.611184                

Abstract

We provide necessary conditions in order that the Hamiltonian systems with Hamiltonian , and one of the following potentials  are integrable in the Liouville sense.

Keywords

Hamiltonian System, Liouville Integrability, Darboux Points, Homogeneous Potentials of Degree Zero

1. Introduction

In this paper we consider classical Hamiltonian systems with two degrees of freedom for which the Hamiltonian is of the form

$H=\frac{1}{2}\left(p_1^2+p_2^2\right)+V\left(q_1,q_2\right),$ (1)

where V is a homogeneous function of degree 0. Although these systems arising from physics and applied sciences are generally understood to involve only real variables, we will assume that the Hamiltonian system associated to (1) is defined on the complex symplectic manifold $M={ℂ}^4\backslash \Sigma$ equipped with the canonical symplectic form

$\omega ={\displaystyle \underset{j=1}{\overset{2}{\sum }}}d{q}_j\wedge d{p}_j,$

where $\Sigma$ is a set of zero Lebesgue measure.

We will assume that the system of equations

$\text{grad}V\left(q_1\mathrm{,}{q}_2\right)=V^{\prime }\left(q_1\mathrm{,}{q}_2\right)=\left(q_1\mathrm{,}{q}_2\right)\mathrm{,}$

has a nonzero solution $d=\left(d_1\mathrm{,}{d}_2\right)\in {ℂ}^2$ , called a Darboux point of the potential V.

A Hamiltonian system of two degrees of freedom is integrable in the Liouville sense if there exists a first integral F, defined in ${ℂ}^4$ except perhaps in a set of zero Lebesgue measure, which is independent with the Hamiltonian, i.e. the rank of the matrix

$\left(\begin{array}{cccc}\frac{\partial H}{\partial q_1}& \frac{\partial H}{\partial q_2}& \frac{\partial H}{\partial p_1}& \frac{\partial H}{\partial p_2}\\ \frac{\partial F}{\partial q_1}& \frac{\partial F}{\partial q_2}& \frac{\partial F}{\partial p_1}& \frac{\partial F}{\partial p_2}\end{array}\right)$

is 2, except perhaps in a zero Lebesgue measure set of ${ℂ}^4$.

The aim of this paper is to find necessary conditions for the integrability of some homogeneous potentials of degree of homogeneity 0. More precisely, our main results are the following.

Proposition 1 Assume that a Hamiltonian system of two degrees of freedom with Hamiltonian of the form (1) and potential

$V=\frac{a_0{q}_1+a_1{q}_2}{a_2{q}_1+a_3{q}_2},$ (2)

where $a_j=b_{j,1}+i{b}_{j,2}\in ℂ$ for $j=0,1,2,3$ , is integrable in the Liouville sense, and that it has Darboux points. If $a_3\ne 0$ , then

$\begin{array}{l}{b}_{01}=\frac{b_{11}\left(b_{21}{b}_{31}+b_{22}{b}_{32}\right)}{b_{31}^2+b_{32}^2}-\frac{b_{12}\left(b_{22}{b}_{31}-b_{21}{b}_{32}\right)}{b_{31}^2+b_{32}^2},\\ b_{02}=-\frac{b_{11}\left(b_{21}{b}_{32}-b_{22}{b}_{31}\right)}{b_{31}^2+b_{32}^2}+\frac{b_{12}\left(b_{21}{b}_{31}+b_{22}{b}_{32}\right)}{b_{31}^2+b_{32}^2}.\end{array}$ (3)

If $a_3=0$ is a particular case of Proposition 3.

Proposition 2 Assume that a Hamiltonian system of two degrees of freedom with Hamiltonian of the form (1) and potential

$V=\frac{a_0{q}_1^2+a_1{q}_1{q}_2+a_2{q}_2^2}{a_3{q}_1^2+a_4{q}_1{q}_2+a_5{q}_2^2},$ (4)

where $a_j=b_{i,1}+i{b}_{j,2}\in ℂ$ for $j=0,\cdots ,5$ , is integrable in the Liouville sense, that it has Darboux points. If $a_5\ne 0$ , then

$\begin{array}{l}{b}_{01}=\frac{b_{21}{b}_{31}{b}_{51}+b_{21}{b}_{32}{b}_{52}+b_{22}{b}_{31}{b}_{52}-b_{22}{b}_{32}{b}_{51}}{b_{51}^2+b_{52}^2},\\ b_{02}=-\frac{b_{21}{b}_{31}{b}_{52}-b_{21}{b}_{32}{b}_{51}-b_{22}{b}_{31}{b}_{51}-b_{22}{b}_{32}{b}_{52}}{b_{51}^2+b_{52}^2},\\ b_{11}=\frac{b_{21}{b}_{41}{b}_{51}+b_{21}{b}_{42}{b}_{52}+b_{22}{b}_{41}{b}_{52}-b_{22}{b}_{42}{b}_{51}}{b_{51}^2+b_{52}^2},\\ b_{12}=\frac{-b_{21}{b}_{41}{b}_{52}+b_{21}{b}_{42}{b}_{51}+b_{22}{b}_{41}{b}_{51}+b_{22}{b}_{42}{b}_{52}}{b_{51}^2+b_{52}^2}.\end{array}$ (5)

If $a_5=0$ , then

$b_{01}=b_{21},b_{02}=b_{22}\text{and}{b}_{11}=b_{12}=0.$ (6)

Proposition 3 If a Hamiltonian system of two degrees of freedom with Hamiltonian of the form (1) and potential

$V=\frac{a_0{q}_2^n+a_1{q}_2^{n-1}{q}_1+\cdots +a_n{q}_1^n}{q_1^n},$ (7)

where $a_j=b_{j,1}+i{b}_{j,2}\in ℂ$ for $j=0,\cdots ,n$ , is integrable in the Liouville sense and has Darboux points, then it satisfies

$\begin{array}{l}{b}_{1,1}=-{\displaystyle \underset{k=1}{\overset{\left[\left(n-1\right)/2\right]}{\sum }}}{b}_{2k+1,1}{\left(2k+1\right)}^2{\left(-1\right)}^k,b_{2,1}={\displaystyle \underset{k=2}{\overset{\left[n/2\right]}{\sum }}}{b}_{2k,1}{k}^2{\left(-1\right)}^k,\\ b_{1,2}=-{\displaystyle \underset{k=1}{\overset{\left[\left(n-1\right)/2\right]}{\sum }}}{b}_{2k+1,2}{\left(2k+1\right)}^2{\left(-1\right)}^k,b_{2,2}={\displaystyle \underset{k=2}{\overset{\left[n/2\right]}{\sum }}}{b}_{2k,2}{k}^2{\left(-1\right)}^k.\end{array}$ (8)

These three propositions are proved in Section 3. The proof of Proposition 2 needs the help of an algebraic manipulator like mathematica for doing it, and a such manipulator also helps in the proof of Proposition 1 but there is not strictly necessary.

The integrability of other Hamiltonian systems with two degrees of freedom and different potentials have been studied in [1] - [30] .

2. Preliminary Results

It was proved in Theorem 1.2 of [31] the following result for Hamiltonian systems with n degrees of freedom of the form (1) with homogeneous potentials of degree 0.

Theorem 4 Assume that $V\in ℂ\left[q_1\mathrm{,}\cdots \mathrm{,}{q}_n\right]$ is homogeneous of degree 0 and that the following conditions are satisfied:

1) there exists a non-zero $d=\left(d_1\mathrm{,}\cdots \mathrm{,}{d}_n\right)\in {ℂ}^n$ such that $V^{\prime }\left(d_1\mathrm{,}\cdots \mathrm{,}{d}_n\right)=\left(d_1\mathrm{,}\cdots \mathrm{,}{d}_n\right)$ , and

2) the system is integrable in the Liouville sense with rational first integrals.

Then

1) all eigenvalues of the Hessian matrix $V^{″}\left(d_1\mathrm{,}\cdots \mathrm{,}{d}_n\right)$ are integers; and

2) the matrix $V^{″}\left(d_1\mathrm{,}\cdots \mathrm{,}{d}_n\right)$ is diagonalizable.

When $n=2$ Theorem 4 has the following easier formulation given in section 5 of [31]

Theorem 5 Assume that $V\in ℂ\left[q_1\mathrm{,}{q}_2\right]$ is homogeneous of degree 0 and that the following conditions are satisfied:

1) there exists a non-zero $d=\left(d_1\mathrm{,}{d}_2\right)\in {ℂ}^2$ such that $V^{\prime }\left(d_1\mathrm{,}{d}_2\right)=\left(d_1\mathrm{,}{d}_n\right)$ , and

2) the system is integrable in the Liouville sense with rational first integrals.

Let $z=q_2/q_1$ with $q_1\ne 0$ , be the affine coordinate on $ℂP^1$ and set $v\left(z\right)\mathrm{<mo>\; :\; </mo>}=V\left(\mathrm{1,}z\right)$. Then the Darboux points are $\pm i$ , and the function v satisfies

$v^{\prime }\left(z_{\mathrm{<mo>\; *\; </mo>}}\right)+z_{\mathrm{<mo>\; *\; </mo>}}{v}^{″}\left(z_{\mathrm{<mo>\; *\; </mo>}}\right)=0.$ (9)

Proof. Darboux points of V are non-zero solutions of equations

$\frac{\partial V}{\partial q_1}=q_1,\frac{\partial V}{\partial q_2}=q_2.$ (10)

It is convenient to consider Darboux points in the projective line $ℂP^1$. Let $z=q_2/q_1$ with $q_1\ne 0$ , be the affine coordinate on $ℂP^1$. Then we can rewrite system (10) in the form

$v^{\prime }\left(z\right)z=-q_1^2\mathrm{,}{v}^{\prime }\left(z\right)=z{q}_1^2\mathrm{,}$ (11)

where $v\left(z\right):=V\left(1,z\right)$. From the above formulae it follows that $z_{\mathrm{<mo>\; *\; </mo>}}$ is a Darboux point of V if and only if $z_{\mathrm{<mo>\; *\; </mo>}}\in \left\{-i\mathrm{,}i\right\}$ , and $v^{\prime }\left(z_{\mathrm{<mo>\; *\; </mo>}}\right)\ne 0$. Thus the location of the Darboux points does not depend on the potential.

If $z_{\mathrm{<mo>\; *\; </mo>}}$ is the affine coordinate of the Darboux point $d=\left(d_1,d_2\right)$ of V, then the Hessian matrix $V^{″}\left(d\right)$ expressed in this coordinate has the form

$V^{″}\left(d\right)\mathrm{<mo>\; =\; </mo>}\left(\begin{array}{cc}-v^{″}\left(z_{\mathrm{<mo>\; *\; </mo>}}\right)x_{\mathrm{<mo>\; *\; </mo>}}^{-2}-2& -\left[v^{\prime }\left(z_{\mathrm{<mo>\; *\; </mo>}}\right)+z_{\mathrm{<mo>\; *\; </mo>}}{v}^{″}\left(z_{\mathrm{<mo>\; *\; </mo>}}\right)\right]x_{\mathrm{<mo>\; *\; </mo>}}^{-2}\\ -\left[v^{\prime }\left(z_{\mathrm{<mo>\; *\; </mo>}}\right)+z_{\mathrm{<mo>\; *\; </mo>}}{v}^{″}\left(z_{\mathrm{<mo>\; *\; </mo>}}\right)\right]x_{\mathrm{<mo>\; *\; </mo>}}^{-2}& v^{″}\left(z_{\mathrm{<mo>\; *\; </mo>}}\right)x_{\mathrm{<mo>\; *\; </mo>}}^{-2}\end{array}\right)\mathrm{,}$

where

$x_{*}=-v^{\prime }\left(z_{*}\right)z_{*}=v^{\prime }\left(z_{*}\right)/z_{*}.$

Vector d is an eigenvector of $V^{″}\left(d\right)$ with corresponding eigenvalue $\lambda =-1$. As the trace of $V^{″}\left(d\right)$ is −2, $\lambda =-1$ is the only eigenvalue of $V^{″}\left(d\right)$. Thus the first hypothesis of Theorem 4 is satisfied, and the second also by our assumptions, then the matrix $V^{″}\left(d\right)$ is diagonalizable, and since its eigenvalues are −1 and −1, we get that $V^{″}\left(d\right)$ is diagonal. Hence the second condition of Theorem 4 is satisfied if and only if (9) holds.

3. Proof of the Propositions

Proof of Proposition 1. We will apply Theorem 5 to potential (2). Then it has the Darboux points $\pm i$. Since

$v\left(z\right)=\frac{a_0+a_{1}z}{a_2+a_{3}z},$

we have

$v^{\prime }\left(z\right)+z{v}^{″}\left(z\right)=\frac{\left(a_1{a}_2-a_0{a}_3\right)\left(a_2-a_{3}z\right)}{{\left(a_2+a_{3}z\right)}^3}.$

Taking $a_j=b_{j,1}+i{b}_{j,2}$ for $j=0,\cdots ,3$ , the condition (9) implies

$\frac{\left(b_{21}+i{b}_{22}-i\left(b_{31}+i{b}_{32}\right)\right)\left(\left(b_{11}+i{b}_{12}\right)\left(b_{21}+i{b}_{22}\right)-\left(b_{01}+i{b}_{02}\right)\left(b_{31}+i{b}_{32}\right)\right)}{{\left(b_{21}+i{b}_{22}+i\left(b_{31}+i{b}_{32}\right)\right)}^3}=0$ (12)

and

$\frac{\left(b_{21}+i{b}_{22}+i\left(b_{31}+i{b}_{32}\right)\right)\left(\left(b_{11}+i{b}_{12}\right)\left(b_{21}+i{b}_{22}\right)-\left(b_{01}+i{b}_{02}\right)\left(b_{31}+i{b}_{32}\right)\right)}{{\left(b_{21}+i{b}_{22}-i\left(b_{31}+i{b}_{32}\right)\right)}^3}=0.$ (13)

Taking the real part and the imaginary part of (12) we get

$\begin{array}{l}-b_{01}{b}_{21}^2{b}_{31}-2b_{01}{b}_{21}{b}_{31}{b}_{32}-b_{01}{b}_{22}^2{b}_{31}-2b_{01}{b}_{22}{b}_{32}^2+b_{01}{b}_{31}^3+b_{01}{b}_{31}{b}_{32}^2\\ +b_{02}{b}_{21}^2{b}_{32}-2b_{02}{b}_{21}{b}_{31}^2+b_{02}{b}_{22}^2{b}_{32}-2b_{02}{b}_{22}{b}_{31}{b}_{32}-b_{02}{b}_{31}^2{b}_{32}-b_{02}{b}_{32}^3\\ +b_{11}{b}_{21}^3+b_{11}{b}_{21}{b}_{22}^2+2b_{11}{b}_{21}{b}_{22}{b}_{31}-b_{11}{b}_{21}{b}_{31}^2-b_{11}{b}_{21}{b}_{32}^2+2b_{11}{b}_{22}^2{b}_{32}\\ -b_{12}{b}_{21}^2{b}_{22}+2b_{12}{b}_{21}^2{b}_{31}+2b_{12}{b}_{21}{b}_{22}{b}_{32}-b_{12}{b}_{22}^3+b_{12}{b}_{22}{b}_{31}^2+b_{12}{b}_{22}{b}_{32}^2=0\end{array}$

and

$\begin{array}{l}-b_{01}{b}_{21}^2{b}_{32}+2b_{01}{b}_{21}{b}_{31}^2-b_{01}{b}_{22}^2{b}_{32}+2b_{01}{b}_{22}{b}_{31}{b}_{32}+b_{01}{b}_{31}^2{b}_{32}+b_{01}{b}_{32}^3\\ -b_{02}{b}_{21}^2{b}_{31}-2b_{02}{b}_{21}{b}_{31}{b}_{32}-b_{02}{b}_{22}^2{b}_{31}-2b_{02}{b}_{22}{b}_{32}^2+b_{02}{b}_{31}^3+b_{02}{b}_{31}{b}_{32}^2\\ +b_{11}{b}_{21}^2{b}_{22}-2b_{11}{b}_{21}^2{b}_{31}-2b_{11}{b}_{21}{b}_{22}{b}_{32}+b_{11}{b}_{22}^3-b_{11}{b}_{22}{b}_{31}^2-b_{11}{b}_{22}{b}_{32}^2\\ +b_{12}{b}_{21}^3+b_{12}{b}_{21}{b}_{22}^2+2b_{12}{b}_{21}{b}_{22}{b}_{31}-b_{12}{b}_{21}{b}_{31}^2-b_{12}{b}_{21}{b}_{32}^2+2b_{12}{b}_{22}^2{b}_{32}=0.\end{array}$

Taking the real part and the imaginary part of (13) we get

$\begin{array}{l}-b_{01}{b}_{21}^2{b}_{31}+2b_{01}{b}_{21}{b}_{31}{b}_{32}-b_{01}{b}_{22}^2{b}_{31}+2b_{01}{b}_{22}{b}_{32}^2+b_{01}{b}_{31}^3+b_{01}{b}_{31}{b}_{32}^2\\ +b_{02}{b}_{21}^2{b}_{32}+2b_{02}{b}_{21}{b}_{31}^2+b_{02}{b}_{22}^2{b}_{32}+2b_{02}{b}_{22}{b}_{31}{b}_{32}-b_{02}{b}_{31}^2{b}_{32}-b_{02}{b}_{32}^3\\ +b_{11}{b}_{21}^3+b_{11}{b}_{21}{b}_{22}^2-2b_{11}{b}_{21}{b}_{22}{b}_{31}-b_{11}{b}_{21}{b}_{31}^2-b_{11}{b}_{21}{b}_{32}^2-2b_{11}{b}_{22}^2{b}_{32}\\ -b_{12}{b}_{21}^2{b}_{22}-2b_{12}{b}_{21}^2{b}_{31}-2b_{12}{b}_{21}{b}_{22}{b}_{32}-b_{12}{b}_{22}^3+b_{12}{b}_{22}{b}_{31}^2+b_{12}{b}_{22}{b}_{32}^2=0\end{array}$

and

$\begin{array}{l}-b_{01}{b}_{21}^2{b}_{32}-2b_{01}{b}_{21}{b}_{31}^2-b_{01}{b}_{22}^2{b}_{32}-2b_{01}{b}_{22}{b}_{31}{b}_{32}+b_{01}{b}_{31}^2{b}_{32}+b_{01}{b}_{32}^3\\ -b_{02}{b}_{21}^2{b}_{31}+2b_{02}{b}_{21}{b}_{31}{b}_{32}-b_{02}{b}_{22}^2{b}_{31}+2b_{02}{b}_{22}{b}_{32}^2+b_{02}{b}_{31}^3+b_{02}{b}_{31}{b}_{32}^2\\ +b_{11}{b}_{21}^2{b}_{22}+2b_{11}{b}_{21}^2{b}_{31}+2b_{11}{b}_{21}{b}_{22}{b}_{32}+b_{11}{b}_{22}^3-b_{11}{b}_{22}{b}_{31}^2-b_{11}{b}_{22}{b}_{32}^2\\ +b_{12}{b}_{21}^3+b_{12}{b}_{21}{b}_{22}^2-2b_{12}{b}_{21}{b}_{22}{b}_{31}-b_{12}{b}_{21}{b}_{31}^2-b_{12}{b}_{21}{b}_{32}^2-2b_{12}{b}_{22}^2{b}_{32}=0.\end{array}$

Solving these four equations we obtain that the condition (3) given in the statement of Proposition 1.

Proof of Proposition 2. We will apply Theorem 5 to potential (4). First assume that $a_5\ne 0$. Therefore this potential has the Darboux points $\pm i$. Since

$v\left(z\right)=\frac{a_0+a_{1}z+a_2{z}^2}{a_3+a_{4}z+a_5{z}^2},$

we obtain

$\begin{array}{l}{v}^{\prime }\left(z\right)+z{v}^{″}\left(z\right)\\ =\frac{1}{{\left(a_3+z\left(a_4+a_{5}z\right)\right)}^3}(a_0\left(z\left(a_4^2+3a_4{a}_{5}z+4a_5^2{z}^2\right)-a_3\left(a_4+4a_{5}x\right)\right)\\ +a_1\left(a_3^2-a_{3}z\left(a_4+6a_{5}z\right)+a_5{z}^3\left(a_{5}z-a_4\right)\right)\\ +a_{2}z\left(4a_3^2+a_{3}z\left(3a_4-4a_{5}x\right)+a_4{z}^2\left(a_4-a_{5}z\right)\right))\\ =0.\end{array}$

By condition (9) on v and since $a_j=b_{j,1}+i{b}_{j,2}$ for $j=0,\cdots ,5$ , we get

(14)

and

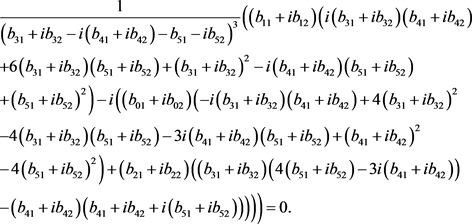(15)

Taking the real part and the imaginary parts of (14) and (15) and solving the corresponding equations with the help of an algebraic manipulator such as Mathematica we get the unique solution given in (5).

Now we assume that. In this case

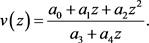
Then

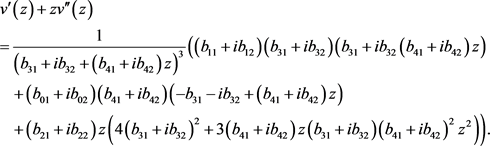
By condition (9) on v and since for, we get

(16)

and

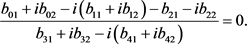(17)

Taking the real part and the imaginary parts of (16) and (17) and solving the corresponding equations with the help of an algebraic manipulator such as Mathematica we get the unique solution given in (6).

Proof of Proposition 3. We will apply Theorem 5 to potential (7). Then its Darboux points are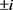. Since

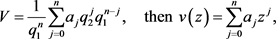
and consequently

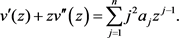
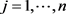Now applying condition (9) on v and taking into account that for, we get

which yields

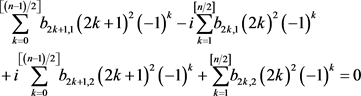
and

Therefore

Hence

This yields (8).

4. Conclusions

We have characterized the Liouville integrability of the Hamiltonian systems with Hamiltonian

and one of the following potentials

For doing this we have used the Darboux theory of integrability.

Acknowledgements

The first author is partially supported by the Ministerio de Economía, Industria y Competitividad, Agencia Estatal de Investigación grants MTM2016-77278-P (FEDER) and MDM-2014-0445, the Agència de Gestió d’Ajuts Universitaris i de Recerca grant 2017SGR1617, and the H2020 European Research Council grant MSCA-RISE-2017-777911. The second author is partially supported by FCT/Portugal through UID/MAT/ 04459/2013.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Boundis, T., Segur, H. and Vivaldi, F. (1982) Integrable Hamiltonian Systems and the Painlevé Property. Physical Review A, 25, 1257-1264. https://doi.org/10.1103/PhysRevA.25.1257
[2]	Chang, Y.F., Tabor, M. and Weiss, J. (1982) Analytic Structure of the Hénon-Heiles Hamiltonian in Integrable and Nonintegrable Regimes. Journal of Mathematical Physics, 23, 531-538. https://doi.org/10.1063/1.525389
[3]	Christopher, C., Llibre, J. and Pereira, J.V. (2007) Multiplicity of Invariant Algebraic Curves in Polynomial Vector Fields. Pacific Journal of Mathematics, 229, 63-117. https://doi.org/10.2140/pjm.2007.229.63
[4]	Darboux, G. (1878) Mémoire sur les équations différentielles du premier ordre et du premier degreé (Mélanges). Bulletin des Sciences Mathématiques, 2, 60-96, 123-144, 151-200.
[5]	Darboux, G. (1878) De l'emploi des solutions particulières algébriques dans l'intégration des systèmes d'équations différentielles algébriques. Comptes rendus de l’Académie des Sciences, 86, 1012-1014.
[6]	Dumortier, F., Llibre, J. and Artés, J.C. (2006) Qualitative Theory of Planar Differential Systems. Universitext. Springer-Verlag, Berlin.
[7]	Furta, S.D. (1996) On Non-Integrability of General Systems of Differential Equations. Zeitschrift für angewandte Mathematik und Physik, 47, 112-131. https://doi.org/10.1007/BF00917577
[8]	Gonzalez-Gascon, F. (1988) A Word of Caution Concerning the Yoshida Criterion on Algebraic Integrability and Kowalevski Exponents. Celestial Mechanics and Dynamical Astronomy, 44, 309-311. https://doi.org/10.1007/BF01234269
[9]	Goriely, A. (1996) Integrability, Partial Integrability, and Nonintegrability for Systems of Ordinary Differential Equations. Journal of Mathematical Physics, 37, 1871-1893. https://doi.org/10.1063/1.531484
[10]	Grammaticos, B., Dorizzi, B. and Padjen, R. (1982) Painlevé Property and Integrals of Motion for the Hénon-Heiles System. Physics Letters A, 89, 111-113. https://doi.org/10.1016/0375-9601(82)90868-4
[11]	Hall, L.S. (1983) A Theory of Exact and Approximate Configurational Invariants. Journal of Physics D, 8, 90-116. https://doi.org/10.1016/0167-2789(83)90312-3
[12]	Hietarinta, J. (1983) A Search for Integrable Two Dimensional Hamiltonian Systems with Polynomial Potential. Physics Letters A, 96, 273-278. https://doi.org/10.1016/0375-9601(83)90178-0
[13]	Hietarinta, J. (1987) Direct Methods for the Search of the Second Invariant. Physics Reports, 147, 87-154. https://doi.org/10.1016/0370-1573(87)90089-5
[14]	Llibre, J., Mahdi, A. and Valls, C. (2011) Analytic Integrability of Hamiltonian Systems with a Homogeneous Polynomial Potential of Degree 4. Journal of Mathematical Physics, 52, Article ID: 012702. https://doi.org/10.1063/1.3544473
[15]	Llibre, J., Mahdi, A. and Valls, C. (2011) Polynomial Integrability of the Hamiltonian Systems with Homogeneous Potential of Degree-2. Physics Letters A, 375, 1845-1849. https://doi.org/10.1016/j.physleta.2011.03.042
[16]	Llibre, J., Mahdi, A. and Valls, C. (2011) Polynomial Integrability of the Hamiltonian Systems with Homogeneous Potential of Degree-3. Physics D, 240, 1928-1935. https://doi.org/10.1016/j.physd.2011.09.003
[17]	Llibre, J. and Peralta-Salas, D. (2012) A Note on the First Integrals of Vector Fields with Integrating Factors and Normalizers. SIGMA, 8, 1-9.
[18]	Llibre, J. and Valls, C. (2014) Darboux Integrability of 2-Dimensional Hamiltonian Systems with Homogenous Potentials of Degree 3. Journal of Mathematical Physics, 55, Article ID: 033507.
[19]	Llibre, J. and Valls, C. (2015) Analytic Integrability of Hamiltonian Systems with Exceptional Potentials. Physics Letters A, 379, 2295-2299. https://doi.org/10.1016/j.physleta.2015.07.034
[20]	Llibre, J. and Valls, C. (2017) On the Integrability of Hamiltonian Systems with d Degrees of Freedom and Homogenous Polynomial Potential of Degree n, to Appear in Communications in Contemporary Mathematics.
[21]	Llibre, J. and Zhang, X. (2002) Polynomial First Integrals for Quasi-Homogeneous Polynomial Differential Systems. Nonlinearity, 15, 1269-1280. https://doi.org/10.1088/0951-7715/15/4/313
[22]	Llibre, J. and Zhang, X. (2009) Darboux Theory of Integrability for Polynomial Vector Fields in Rn Taking into Account Their Multiplicity at Infinity. Bulletin des Sciences Mathématiques, 133, 765-778. https://doi.org/10.1016/j.bulsci.2009.06.002
[23]	Maciejewski, A.J. and Przybylska, M. (2004) All Meromorphically Integrable 2D Hamiltonian Systems with Homogeneous Potential of Degree 3. Physics Letters A, 327, 461-473.
[24]	Maciejewski, A.J. and Przybylska, M. (2005) Darboux Points and Integrability of Hamiltonian Systems with Homogeneous Polynomial Potential. Journal of Mathematical Physics, 46, Article ID: 062901.
[25]	Morales Ruiz, J.J. (1999) Differential Galois Theory and Non-Integrability of Hamiltonian Systems. Progress in Mathematics, Vol. 179, Birkhauser Verlag, Basel. https://doi.org/10.1007/978-3-0348-0723-4
[26]	Ramani, A., Dorizzi, B. and Grammaticos, B. (1982) Painlevé Conjecture Revisited. Physical Review Letters, 49, 1539-1541. https://doi.org/10.1103/PhysRevLett.49.1539
[27]	Tsygvintsev, A. (2001) On the Existence of Polynomial First Integrals of Quadratic Homogeneous Systems of Ordinary Differential Equations. Journal of Physics A: Mathematical and General, 34, 2185-2193. https://doi.org/10.1088/0305-4470/34/11/311
[28]	Yoshida, H. (1983) Necessary Conditions for Existence of Algebraic First Integrals I and II. Celestial Mechanics, 31, 363-379, 381-399. https://doi.org/10.1007/BF01230292
[29]	Yoshida, H. (1988) A Note on Kowalevski Exponents and the Non-Existence of an Additional Analytic Integral. Celestial Mechanics, 44, 313-316. https://doi.org/10.1007/BF01234270
[30]	Yoshida, H. (1989) A Criterion for the Non-Existence of an Additional Analytic Integral in Hamiltonian Systems with n Degrees of Freedom. Physics Letters A, 141, 108-112. https://doi.org/10.1016/0375-9601(89)90768-8
[31]	Casale, G., Duval, G., Maciejewski, A.J. and Przybylska, M. (2010) Integrability of Hamiltonian Systems with Homogenous Potential of Degree Zero. Physics Letters A, 374, 448-452. https://doi.org/10.1016/j.physleta.2009.11.018