On Semi π-Regular Local Ring

Zubayda M. Ibraheem, Raghad A. Mustafa, Maha F. Khalf

Department of Mathematics, College of Computer and Mathematical Sciences, University of Mosul, Mosul, Iraq.

DOI: 10.4236/oalib.1104788                

Abstract

A ring R is said to be a right (left) semi π-regular local ring if and only if for all a in R, either a or (1-a) is a right (left) semi π-regular element. The purpose of this paper is to give some characterization and properties of semi π-regular local rings, and to study the relation between semi π-regular local rings and local rings. From the main results of this work: 1) Let R be a semi π-regular reduced ring. Then the idempotent associated element is unique. 2) Let R be a ring. Then R is a right semi π-regular local ring if and only if either r(aⁿ) or r((1-a)ⁿ) is direct summand for all a∈R and n∈Z . If R is a local ring withr(aⁿ) r(a) for all a∈R and n∈Z , then R is a right semi π-regular local ring.

Keywords

Local, Ring, Semi π-Regular

1. Introduction

Throughout this paper, R will be an associative ring with identity. For $a\in R$, $r\left(a\right)$, $\left(l\left(a\right)\right)$ denote the right (left) annihilator of a. A ring R is reduced if R contains, no non-zero nilpotent element.

A ring R is said to be Von Neumann regular (or just regular) if and only if for each a in R, there exists b in R such that $a=aba$ [1] . Following [2] , a ring R is said to be right semi-regular if and only if for each a in R, there exists b in R such that $a=ab$ and $r\left(a\right)=r\left(b\right)$ .

By extending the notion of a right semi π-regular ring to a right semi-regular ring is defined as follows:

A ring R is said to be right semi π-regular if and only if for each a in R, there exist positive integers n and b in R such that $a^n=a^{n}b$ and $r\left(a^n\right)=r\left(b\right)$ [3] .

Following [4] , a ring R is said to be π-regular if and only if for each a in R, there exist positive integers n and b in R such that $a^n=a^{n}b{a}^n$ . A ring R is called a local ring, if it has exactly one maximal ideal [5] .

A ring R is said to be a local semi-regular ring, if for all a in R, either a or $\left(1-a\right)$ is a semi-regular element [6] .

We extend the notion of the local semi-regular ring to the semi π-regular local ring defined as follows:

A ring R is said to be a semi π-regular local ring, if for all a in R, either a or $\left(1-a\right)$ is a semi π-regular element.

Clearly that every π-regular ring is a semi π-regular local ring.

2. A Study of Some Characterization of Semi π-Regular Local Ring

In this section we give the definition of a semi π-regular local ring with some of its characterization and basic properties.

2.1. Definition

A ring R is said to be right (left) semi π-regular local ring if and only if for all a in R, either a or $\left(1-a\right)$ is right (left) semi π-regular element for every a in R.

Examples:

Let $\left(Z_2,+,\cdot \right)$ be a ring and let $G=\left\{g:g^2=1\right\}$ is cyclic group, then $Z_{2}G=\left\{0,1,g,1+g\right\}$ is π-regular ring. Thus R is semi π-regular local ring.

Let R be the set of all matrix in $Z_2$ which is defined as:

$R=\left\{\left[\begin{array}{cc}a& b\\ 0& d\end{array}\right]:a,b,d\in Z_2\right\}$ .

It easy to show that R is semi π-regular local ring.

2.2. Proposition

Let R be a right semi π-regular local ring. Then the associated elements are idempotents.

Proof:

Let $a\in R$, since R is right semi π-regular local ring. Then either a or $\left(1-a\right)$ is right semi π-regular element, that there exists b in R such that $a^n=a^{n}b$ and $r\left(a^n\right)=r\left(b\right)$, so $a^n\left(1-b\right)=0$, gives $\left(1-b\right)\in r\left(a^n\right)=r\left(b\right)$ . Thus $b\left(1-b\right)=0$, which implies $b=b^2$ . Now, if $\left(1-a\right)$ is right semi π-regular element, then there exists c in R such that ${\left(1-a\right)}^n={\left(1-a\right)}^n{c}^c$ and $r\left({\left(1-a\right)}^n\right)=r\left(c\right)$ . So ${\left(1-a\right)}^n\left(1-c\right)=0$, thus $\left(1-c\right)\in r\left({\left(1-a\right)}^n\right)=r\left(c\right)$ . Hence $c\left(1-c\right)=0$ and therefore $c=c^2$ .

In general the associated element is not unique. But the following proposition give the necessary condition to prove the associated element is unique.

2.3. Proposition

Let R be a right semi π-regular local reduced ring. Then the idempotent associated element is unique.

Proof:

Let $a\in R$, since R is right semi π-regular local ring. Then either a or $\left(1-a\right)$ is right semi π-regular element in R. If a is right semi π-regular element, then there exists $b\in R$ such that $a^n=a^{n}b$ and $r\left(a^n\right)=r\left(b\right)$ . Assume that, there is an element $\bar{b}$ in R such that $a^n=a^n\bar{b}$ and $r\left(a^n\right)=r\left(\bar{b}\right)$, which implies that $a^n\left(b-\bar{b}\right)=0$, hence $\left(b-\bar{b}\right)\in r\left(a^n\right)=r\left(b\right)=r\left(\bar{b}\right)$ and $\bar{b}\left(b-\bar{b}\right)=0$, that is $b\left(b-\bar{b}\right)=0$ and then $\bar{b}b={\bar{b}}^2$, $b^2=b\bar{b}$, which implies $\bar{b}b=\bar{b}$, $b=b\bar{b}$ .

Since R is reduced ring, then $r\left(b\right)=l\left(b\right)=l\left(\bar{b}\right)$ . Hence $\left(b-\bar{b}\right)\in l\left(b\right)=l\left(\bar{b}\right)$ and then $\left(b-\bar{b}\right)b=0$ and $\left(b-\bar{b}\right)\bar{b}=0$ which implies $b^2=b\bar{b}$ and $b\bar{b}={\bar{b}}^2$ . Hence $b=\bar{b}b$ and $b\bar{b}=\bar{b}$, and therefore $b=\bar{b}b=b\bar{b}=\bar{b}$ . Now, if $\left(1-a\right)$ is right semi π-regular element, then there exists an element $c\in R$ such that ${\left(1-a\right)}^n={\left(1-a\right)}^{n}c$ and $r\left({\left(1-a\right)}^n\right)=r\left(c\right)$ . Now, we assume that the associated element c is not unique.

Then, there exists $\bar{c}\in R$ such that $r\left({\left(1-a\right)}^n\right)=r\left(\bar{c}\right)$, ${\left(1-a\right)}^n={\left(1-a\right)}^n\bar{c}$, then ${\left(1-a\right)}^{n}c={\left(1-a\right)}^n\bar{c}$ which implies that ${\left(1-a\right)}^n\left(c-\bar{c}\right)=0$, that is $\left(c-\bar{c}\right)\in r\left({\left(1-a\right)}^n\right)=r\left(c\right)=r\left(\bar{c}\right)$ . Hence $c\left(c-\bar{c}\right)=0$ and $\bar{c}\left(c-\bar{c}\right)=0$, implies that $c^2=c\bar{c}$ and $\bar{c}c={\bar{c}}^2$, that is $c=c\bar{c}$ and $\bar{c}c=\bar{c}$ . Since R is reduced ring, then $l\left(\bar{c}\right)=r\left(c\right)=l\left(c\right)$ and then $\left(c-\bar{c}\right)c=0$, $\left(c-\bar{c}\right)\bar{c}=0$, that is $c^2=\bar{c}c$ and $c\bar{c}={\bar{c}}^2$ . Thus $c=\bar{c}c$ and $c\bar{c}=\bar{c}$ . Therefore $c=\bar{c}c=c\bar{c}=\bar{c}$ .

The following theorem give the condition to a semi π-regular local ring to be π-regular ring.

2.4. Theorem

Let R be a right semi π-regular local ring. Then any element $a\in R$ is π-regular if $R{a}^n=Rb$ for any associated element b in R.

Proof:

Let $a\in R$ and R be a right semi π-regular local ring. Then either or $\left(1-a\right)$ is right semi π-regular element in R. If a is right semi π-regular element in R, then there exists $b\in R$ such that $a^n=a^{n}b$ and $r\left(a^n\right)=r\left(b\right)$ .

Now, assume that $R{a}^n=Rb$ . Then $r{a}^n=b$ and $r{a}^n\in R{a}^n$, $b\in Rb$ . Since b is idempotent element, then $b+\left(1-b\right)=1$ and $r{a}^n+\left(1-b\right)=1$, it follows that $a^n{r}^n{a}^n+a^n\left(1-b\right)=a^n$ .

Thus $a^{n}r{a}^n=a^n$ . Therefore a is π-regular element in R.

Now, if $\left(1-a\right)$ is right semi π-regular element, then there exists an element $c\in R$ such that : ${\left(1-a\right)}^n={\left(1-a\right)}^{n}c$ and $r\left({\left(1-a\right)}^n\right)=r\left(c\right)$ .

If $R{\left(1-a\right)}^n=Rc$, assume that $s\left(1-a^n\right)=c$, where $s\left(1-a\right)\in R\left(1-a\right)$, $c\in R$ . Since c is idempotent element, then $c+\left(1-c\right)=1$ and $S{\left(1-a\right)}^n+\left(1-c\right)=1$, it follows that ${\left(1-a\right)}^{n}S{\left(1-a\right)}^n+{\left(1-a\right)}^n\left(1-c\right)={\left(1-a\right)}^n$, that is ${\left(1-a\right)}^{n}S{\left(1-a\right)}^n+{\left(1-a\right)}^n-{\left(1-a\right)}^{n}c={\left(1-a\right)}^n$ .

Thus ${\left(1-a\right)}^{n}S{\left(1-a\right)}^n={\left(1-a\right)}^n$ . Therefore $\left(1-a\right)$ is π-regular element in R.

2.5. Proposition

The epimorphism image of right semi π-regular local ring is right semi π-regular local ring.

Proof:

Let $f:R\to \bar{R}$ be epimorphism homomorphism function from the ring π in to the ring $\bar{R}$, where R is right semi π-regular local ring and let $\bar{e},y,\bar{1}$ be element s in $\bar{R}$ . Then there exists elements $e,x,1$ in R such that

$f\left(e\right)=\bar{e},f\left(x\right)=y,f\left(1\right)=\bar{1}$ .

Now, since R is right semi π-regular local ring, then either x or $\left(1-x\right)$ is right semi π-regular element, that is $x^n=x^{n}e$ and $r\left(x^n\right)=r\left(e\right)$ . Then

$y^n={\left(f\left(x\right)\right)}^n=f\left(x^n\right)=f\left(x^{n}e\right)=f\left(x^n\right)f\left(e\right)=y^n\bar{e}$ .

Now, to prove $r\left(y^n\right)=r\left(\bar{e}\right)$ . If $a\in r\left(y^n\right)$, then $y^{n}a=0$, that is ${\left(f\left(x\right)\right)}^{n}a=0$, then $f\left(x^n\right)a=0$, and $f^{-1}f\left(x^n\right)f^{-1}\left(a\right)=0$, hence $x^n{f}^{-1}\left(a\right)=0$ .

Thus $f^{-1}\left(a\right)\in r\left(x^n\right)=r\left(e\right)$, that is $e{f}^{-1}\left(a\right)=0$ . Then $f\left(e\right)a=0$, thus $\bar{e}a=0$ . Hence $a\in r\left(\bar{e}\right)$ . Therefore,

$r\left(y^n\right)\subseteq r\left(\bar{e}\right)$ (1)

Now, let $b\in r\left(\bar{e}\right)$ . Then $\bar{e}b=0$, it follows that $y\bar{e}b=0$ and then $y^n\bar{e}b=0$ .

Thus $y^{n}b=0$ and hence $b\in r\left(y^n\right)$ . Therefore

$r\left(\bar{e}\right)\subseteq r\left(y^n\right)$ (2)

from (1) and (2), we obtain $r\left(\bar{e}\right)=r\left(y^n\right)$ .

Now, if $\left(1-x\right)$ is right semi π-regular element in R, then ${\left(1-x\right)}^n={\left(1-x\right)}^{n}e$ and $r{\left(1-x\right)}^n=r\left(e\right)$ .

Now, $f{\left(1-x\right)}^n={\left(f\left(1-x\right)\right)}^n={\left(f\left(1\right)+f\left(-x\right)\right)}^n={\left(f\left(1\right)-f\left(x\right)\right)}^n={\left(\bar{1}-y\right)}^n$ . Thus ${\left(\bar{1}-y\right)}^n=f{\left(1-x\right)}^n=f\left({\left(1-x\right)}^{n}e\right)=f{\left(1-x\right)}^{n}f\left(e\right)={\left(\bar{1}-y\right)}^n\bar{e}$ .

Now, to prove $r{\left(\bar{1}-y\right)}^n=r\left(\bar{e}\right)$ .

Let $c\in r{\left(\bar{1}-y\right)}^n$ . Then ${\left(\bar{1}-y\right)}^{n}c=0$ . That is ${\left(f\left(1\right)-f\left(x\right)\right)}^{n}c=0$, then ${\left(f\left(1-x\right)\right)}^{n}c=0$ and $f{\left(1-x\right)}^{n}c=0$ . Then ${\left(1-x\right)}^n{f}^{-1}\left(c\right)=0$ and hence $f^{-1}\left(c\right)\in r{\left(1-x\right)}^n=r\left(e\right)$, that is $e{f}^{-1}\left(c\right)=0$, it follows that $f\left(e\right)c=0$ .

Hence $\bar{e}c=0$, thus $c\in r\left(\bar{e}\right)$ . Therefore

$r{\left(\bar{1}-y\right)}^n\subseteq r\left(\bar{e}\right)$ (3)

Now, let $d\in r\left(\bar{e}\right)$, implies to $\bar{e}d=0$, hence ${\left(\bar{1}-y\right)}^n\bar{e}d=0$, thus ${\left(\bar{1}-y\right)}^{n}d=0$ . Hence $d\in r{\left(\bar{1}-y\right)}^n$ . Therefore

$r\left(\bar{e}\right)\subseteq r{\left(\bar{1}-y\right)}^n$ (4)

from (3) and (4) we obtain $r\left(\bar{e}\right)=r{\left(\bar{1}-y\right)}^n$, that is either y or 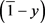is right semi π-regular element in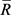. Therefore 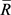is right semi π-regular local ring.

2.6. Theorem

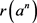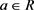Let R be a ring. Then R is right semi π-regular local ring if and only if either or is direct summand for all and.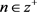

Proof:

Let 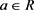and 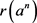is direct summand. Then there exists an ideal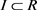, such that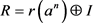. Thus, there is 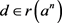and, such that 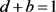and hence 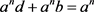and therefore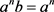. Now, to prove, let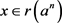. Then, that is and. But and. Then and, hence

(5)

and by the same way we can prove

(6)

from (5) and (6) we obtain. Therefore a is right semi π-regular element. Now, if and is direct summand.

Then, there exists an ideal such that, and there exists and, such that. Thus

.

Therefore. Now, to prove.

Let. Then and hence

Thus,. But and, then and therefore, hence

(7)

Now, let. Then and hence, Thus, therefore and we have

(8)

form (7) and (8) we obtain. Therefore is right semi π-regular element. That is R is right semi π-regular local ring.

Now, let R be aright semi π-regular local ring. Then either a or is right semi π-regular element in R. If a is right semi π-regular element, then there exists and such that and.

Hence, , that is, then and thus. Therefore.

Now, to prove, suppose that, then and. Hence for some and, since, then and, that is [proposition 2.2]. Thus and therefore, that is is direct summand of R.

Now, if is right semi π-regular element, then there exists such that and. Since, we have, and since.

Hence,. Thus,.

Now, to prove. Let.

Then and, hence and for some. Since then and.

Hence [proposition 2.2] and thus and then.

That is. Therefore is direct summand of R.

Now, to give the relation between semi π-regular local ring and local ring.

2.7. Theorem

If R is local ring with for all and, then R is right semi π-regular local ring.

Proof:

Let R be local ring. Then either a or is invertible element in R [6] .

If a is invertible, then there exists an element b in R such that, hence and then. Let. Then. To prove. Let. Then, it follows that and then, that is. Hence

(9)

Now, let. Then and hence that is, thus. Therefore

(10)

from (9) and (10) we obtain. Hence a is right semi π-regular element in R. Now, if is invertible element in R, then there exists an element c in R such that. That is, it follows that. let. Then. To prove, let, then that is and hence, and then. Thus

(11)

Now, let, that is and hence, it follows that, that is. Hence

(12)

form (11) and (12) we have. Thus is right semi π-regular element. Therefore R is right semi π-regular ring.

3. The Conclusion

From the study on characterization and properties of semi π-regular local rings, we obtain the following results:

1) Let R be a right semi π-regular local ring. Then the associated elements are idempotents.

2) Let R be a right semi π-regular local ring. Then the idempotent associated element is unique.

3) Let R be a right semi π-regular local ring. Then any element is π-regular if for any associated element b in R.

4) The epimorphism image of right semi π-regular local ring is right semi π-regular local ring.

5) Let R be a ring. Then R is a right semi π-regular local ring if and only if either or is direct summand for all and.

If R is a local ring with for all and, then R is a right semi π-regular local ring.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Von Neumann, J. (1936) On Regular Rings. Proceedings of the National Academy of Sciences of the United States of America, 22, 707-713. https://doi.org/10.1073/pnas.22.12.707
[2]	Shuker, N.H. (1994) On Semi-Regular Ring. Journal of Education and Science, 21, 183-187.
[3]	Al-Kouri, M.R.M. (1996) On π-Regular Rings. M.Sc. Thesis, Mosul University, Mosul.
[4]	Kim, N.K. and Lee, Y. (2011) On Strongly π-Regularity and π-Regularity. Communications in Algebra, 39, 4470-4485. https://doi.org/10.1080/00927872.2010.524184
[5]	Burton, D.M. (1970) A First Course in Rings and Ideals. Addison Wesley Publishing Company, Boston.
[6]	Abdullah, F.A. (2013) On Local and Local Semi Regular Rings. M.Sc. Thesis, Mosul University, Mosul.