Multi-Period Portfolio Selection with No-Shorting Constraints: Duality Analysis

Jun Qi, Lan Yi

Management School, Jinan University, Guangzhou, China.

DOI: 10.4236/jmf.2017.73040                

Abstract

This paper considers a multi-period mean-variance portfolio selection problem with no shorting constraint. We assume that the sample space is finite, and the possible securities price vector transitions is equivalent to the number of securities. By making use of the embedding technique of Li and Ng (2000), the original nonseparable problem can be solved by introducing an auxiliary problem. After the risk neutral probability is calculated, the auxiliary problem can be solved by using the martingale method of Pliska (1986). Finally, we derive a closed form of the optimal solution to the original constrained problem.

Keywords

Multi-Period Mean-Variance Formulation, Auxiliary Market, Martingale Method, Risk Neutral Probability, Duality, Optimal Trading Strategy

1. Introduction

Portfolio theory deals with the question of how to find an optimal distribution of the wealth among various assets. Mean-variance analysis and expected utility formulation are two different tools for dealing with portfolio selections. A fun- damental basis for portfolio selection in a single period was provided by Mar- kowitz. Under the assumption that short-selling of stocks is not allowed, ana- lytical expression of the mean-variance efficient frontier in single-period port- folio selection was derived by solving a quadratic programming problem in Markowitz (1952) [1] . Later, an analytical solution to the single-period mean- variance problem with assumption that short-selling is allowed is derived in Merton (1972) [2] .

Recently, a multi-period portfolio selection problem has been studied. This problem is more interesting as investors always invest their wealth in multi periods instead of only one period. Work of Li and Ng (2000) [3] considers the multi-period portfolio selection problem in a mean-variance framework when short-selling of stocks is allowed. Li and Ng have derived the analytical formu- lation of the frontier of the multi-period portfolio selection by embedding the assets-only multi-period mean-variance problem into a large tractable problem. When short-selling is not allowed, the multi-period portfolio selection problem is much more difficult to deal with. For continuous-time mean-variance port- folio selections, Xun, Xunyu and Andrew (2002) [4] use stochastic optimal linear-quadratic method. For multi-period setting, the portfolio selection pro- blem with no-shorting constraint has been studied in Xu and Shreve (1992) [5] [6] . These papers investigated a utility maximization problem with a no short- selling constraint using a duality analysis.

The objective of this paper is to investigate dynamic mean-variance portfolio selection when short-selling is not allowed. Instead of using optimization me- thod, this paper used a martingale approach, which was originally proposed by Pliska (1986) [7] . To our knowledge, no analytical numerical method using martingale measure for finding the optimal portfolio policy with no-short shelling constraint for the multiperiod mean-variance formulation has been reported in the literature. In this sense, this paper extends existing literature by utilizing a martingale approach to solve an optimal portfolio selection problem with no-shorting constraint. This approach also showed that a unique equivalent martingale measure exist in the no-arbitrage complete market model. An effec- tive algorithm is derived for finding the maximum quadratic utility function with no-short selling constraint.

To outline of this paper, In Section 2, we build up the security market model. In Section 3, we consider the optimal portfolio selection problem with no short- selling constraint. By transforming the original market to some auxiliary markets, the optimal value of original constrained problem can be derived by the optimal valued of the unconstrained problem in the auxiliary markets. In Section 4, we use martingale approach to solve the unconstrained problem in the auxiliary markets. In Section 5, the optimal terminal wealth was derived by solving a dual problem. In Section 6, the derive the optimal trading strategy based on the optimal terminal wealth. A numerical example is also given in the Section 7. Finally, we conclude the paper.

2. Security Market Model

We consider a multi-period security market model with $T+1$ trading dates (indexed by $\mathrm{0,1,}\cdots \mathrm{,}T$ ), and the time horizon T is finite. There are n risky securities and one bond in the market. Let $\left(\Omega \mathrm{,}\mathcal{F}\mathrm{,}P\right)$ be the probability space. Suppose there are finite states of the world, and let $K\left(t\right)=\left\{\mathrm{1,2,}\cdots \mathrm{,}N\left(t\right)\right\}$ be the state space of the economy at time t. The sample space $\Omega$ of the economy has a finite number of element $\omega =\left\{e_1,e_2,\cdots ,e_T\right\}$ with $e_t\in K\left(t\right)$ . The filtra- tion $F=\left\{{\mathcal{F}}_t\mathrm{,}t=\mathrm{0,1,}\cdots \mathrm{,}T\right\}$ where ${\mathcal{F}}_t$ is generated by $\left\{e_1\mathrm{,}{e}_2\mathrm{,}\cdots \mathrm{,}{e}_T\right\}$ reveals the information on the economy. Specifically, ${\mathcal{F}}_0=\left\{\varnothing \mathrm{,}\Omega \right\}$ and ${\mathcal{F}}_T=\mathcal{F}$ . We claim that the process $K=\left\{k\left(t\right)\in K\left(t\right)\mathrm{<mo>\; ;\; </mo>0}\le t\le T-1\right\}$ is $\mathcal{F}$ -adapted. For any $A\in \mathcal{F}\backslash \varnothing$ , $P\left(A\right)>0$ .

The $n+1$ securities are traded in the market without transaction cost. Denote the stochastic process of the security price as $S=\left\{S_t\mathrm{<mo>\; ;\; </mo>0}\le t\le T\right\}$ , where $S_t={\left(S_t\left(1\right)\mathrm{,}\cdots \mathrm{,}{S}_t\left(n\right)\right)}^{\prime }$ is a random vector, and the bond price process as $B=\left\{B_t\mathrm{<mo>\; ;\; </mo>0}\le t\le T\right\}$ , where $B_t$ is constant. Let $R=\left\{R_t\mathrm{<mo>\; ;\; </mo>1}\le t\le T\right\}$ be the risky security return process defined by $R_t={\left(R_t\left(1\right)\mathrm{,}\cdots \mathrm{,}{R}_t\left(n\right)\right)}^{\prime }$ and $R_t\left(i\right)=S_t\left(i\right)/S_{t-1}\left(i\right)-1\ge -1$ for $S_{t-1}\left(i\right)>0$ , and $r=\left\{r_t\mathrm{<mo>\; ;\; </mo>1}\le t\le T\right\}$ be the bond return process defined by $r_t=B_t/B_{t-1}-1\ge 0$ with $r_t=r$ for all $t=1,\cdots ,T$ .

Assumption 2.1. 1) The state space at time $t$ has $N\left(t\right)=nt+1$ elements; 2) For any $\omega =\left\{e_1\mathrm{,}{e}_2\mathrm{,}\cdots \mathrm{,}{e}_T\right\}$ , if $e_t=j\in K\left(t\right)$ , then $e_{t+1}\in {\bar{K}}^j\left(t+1\right)=\left\{j\mathrm{,}j+\mathrm{1,}\cdots \mathrm{,}j+n\right\}\subseteq K\left(t+1\right)$ ; 3) Denote a matrix $D$ of the securities’ prices

$D_t^j=\left(\begin{array}{cccc}{B}_t\left(j\right)& S_t\left(\mathrm{1,}j\right)& \cdots & S_t\left(n\mathrm{,}j\right)\\ ⋮& ⋮& \ddots & ⋮\\ B_t\left(j+n\right)& S_t\left(\mathrm{1,}j+n\right)& \cdots & S_t\left(n\mathrm{,}j+n\right)\end{array}\right)$

$rank\left(D_t^j\right)=n+1$ for $t=1,2,\cdots ,T$ and $j\in K\left(t\right)$

The above assumption makes the security market a complete one. We can easily verify that the sample space of the market $\Omega$ has ${\left(n+1\right)}^T$ elements under assumption 2.1.

We consider an investor in the financial market with initial wealth v. She or he follows a self-financing trading strategies

$H=\left\{H_t;t=1,2,\cdots ,T\right\}$

where $H_t={\left(H_t\left(1\right)\mathrm{,}\cdots \mathrm{,}{H}_t\left(n\right)\right)}^{\prime }$ and $H_t\left(i\right)$ is the number of units of the ith risky security held between time $t-1$ and $t$ . The number of money invested in the bond is $h_t$ .

Assumption 2.2. The investor invests her or his wealth in the complete market with no short-selling constraint, that is

$H_t\ge 0\mathrm{<mi>\; </mi>\; <mi>\; </mi>}\text{for}t=\mathrm{1,}\cdots \mathrm{,}T\mathrm{.}$ (1)

Let $V_t$ be the value of portfolio at time $t$ , it satisfies

$V_t=h_t{B}_t+{H^{\prime }}_t{S}_t=V_{t-1}+h_t{B}_{t-1}{r}_t+{H^{\prime }}_t{S}_{t-1}{R}_t\mathrm{,}$ (2)

where

$S_{t-1}=\left(\begin{array}{ccc}{S}_{t-1}\mathrm{<mo\; stretchy="false">\; (\; </mo>1\; <mo\; stretchy="false">\; )\; </mo>}& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & S_{t-1}\left(n\right)\end{array}\right)\mathrm{.}$

For our convenience, we introduce the discounted price process $S^{*}=\left\{S_t^{*};0\le t\le T\right\}$ with $S_t^{\mathrm{<mo>\; *\; </mo>}}={\left(S_t^{\mathrm{<mo>\; *\; </mo>}}\left(1\right)\mathrm{,}\cdots \mathrm{,}{S}_t^{\mathrm{<mo>\; *\; </mo>}}\left(n\right)\right)}^{\prime }$ and $S_t^{\mathrm{<mo>\; *\; </mo>}}\left(i\right)=S_t\left(i\right)/B_t$ . So the discounted value of portfolio is $V^{*}=h_t+{H^{\prime }}_t{S}_t^{*}$ . The change of the discounted prices of risky security is defined as ${\delta }_t\left(i\right)={\left({\delta }_t\left(1\right),\cdots ,{\delta }_t\left(n\right)\right)}^{\prime }$ with ${\delta }_t\left(i\right)=S_t^{\mathrm{<mo>\; *\; </mo>}}\left(i\right)-S_{t-1}^{\mathrm{<mo>\; *\; </mo>}}\left(i\right)$ .

We can also defined the self-financing trading strategies as $\pi =\left\{{\pi }_t;t=1,2,\cdots ,T\right\}$ , where ${\pi }_t={\left({\pi }_t\left(1\right),\cdots ,{\pi }_t\left(n\right)\right)}^{\prime }$ and ${\pi }_t\left(i\right)$ is the fraction of money invested in ith risky security at time $t-1$ . Similarly, the no short-selling requires that ${\pi }_t\left(i\right)$ is non-negative for any $t$ . Therefore, the value of portfolio can be re- written as $V_t=V_{t-1}\left[1+\left(1-{\displaystyle {\sum }_{i=1}^n}{\pi }_t\left(i\right)\right)r_t+{{\pi }^{\prime }}_t{R}_t\right]$ . It is easy to verify that ${\pi }_t={H^{\prime }}_t{S}_{t-1}/V_{t-1}$ .

3. Primal and Auxiliary Problem

The multi-period portfolio optimization problem under mean-variance frame- work in this paper can be formulated as follows:

$\{\begin{array}{ll}max\hfill & E\left(V_T\right)-\omega Var\left(V_T\right)\hfill \\ \text{s}\text{.t}\text{.}\hfill & \left(1\right)\mathrm{<mo>\; \&\; </mo>}\left(2\right)\mathrm{,}\hfill \end{array}$

for $\omega \ge 0$ . Varying the value of $\omega$ yields the set of efficient solutions.

As indicated in Li and Ng (2000), above problem is difficult to be solved directly because of the non-separability in the sense of dynamic programming. In Li and Ng (2000), the relation between the multi-period mean-variance portfolio selection problem with a fixed investment horizon and a separable portfolio selection problem with a quadratic utility function is investigated and the analytical solution is derived by using an embedding scheme. Fortunately, Theorems 1 and 2 in Li and Ng (2000) can be also applied in the current subject with an uncertain investment horizon. We now consider the following auxiliary problem:

$\{\begin{array}{ll}max\hfill & E\left(\lambda V_T-\omega V_T^2\right)\hfill \\ \text{s}\text{.t}\text{.}\hfill & \left(1\right)\mathrm{<mo>\; \&\; </mo>}\left(2\right)\mathrm{,}\hfill \end{array}$

The objective function of the auxiliary problem is equivalent to the quadratic utility function $U\left(x\right)=\beta x-\frac{1}{2}{x}^2$ , $\beta =\frac{\lambda }{2\omega }>0$ . It is concave and twice con- tinuously differentiable function.

Proposition 3.1. 1) The first derivative of $U\left(x\right)$ is $U^{\prime }\left(x\right)=\beta -x$ .

2) The inverse function of $U^{\prime }\left(x\right)$ is $I\left(y\right):=\beta -y$ .

The optimal portfolio problem is to maximize the expectation of $U\left(V_T\right)$ under the no short selling constraint ${\pi }_t\in K=\left\{\pi \in {\Re }^n\mathrm{<mo>\; ;\; </mo>}\pi \ge 0\right\}$ . So the con- strained optimal portfolio problem is:

$\begin{array}{l}maxEU\left(V_T\right)\\ \text{s}\text{.t}\pi \in \mathcal{A}\mathrm{,\; <mi>\; </mi>}{V}_0=v\end{array}$

where $\mathcal{A}$ denote the set of all admissible trading strategies belong in $K$ .

Since there is a no short-selling constraint in the optimal portfolio selection problem, it is difficult to be solved directly by dynamic programming. We will try to solve the problem by introducing unconstraint auxiliary problems.

Denote the support function $\sigma \left(x\right)$ of $K$ by

$\sigma \left(x\right)\equiv \underset{\pi \in K}{sup}\left(-{\pi }^{\prime }x\right)\mathrm{.}$

In order to eliminate the situation $\sigma \left(x\right)=\infty$ , we defined that the effective domain of $\sigma$ is the convex cone $\tilde{K}=\left\{x\in {\Re }^n\mathrm{<mo>\; :\; </mo>}\sigma \left(x\right)<\infty \right\}=\left\{x\in {\Re }^n\mathrm{<mo>\; ;\; </mo>}x\ge 0\right\}$ , and $\sigma \left(x\right)=0$ for $x\in \tilde{K}$ . We introduce the predictable process $\kappa =\left\{{\kappa }_t;t=0,1,\cdots ,T-1\right\}$ with ${\kappa }_t={\left({\kappa }_t\left(1\right)\mathrm{,}\cdots \mathrm{,}{\kappa }_t\left(n\right)\right)}^{\prime }\in \tilde{K}$ for all $t\ge 1$ . Let $\mathcal{N}$ denote the set of all such process $\kappa$ . Define an auxiliary market $M_{\kappa }$ for each $\kappa \in \mathcal{N}$ by modifying the return processes for the bond and the risky securities as:

$\begin{array}{l}{r}_t\to r_t\mathrm{,}t\ge 1\\ R_t\to R_t+B_t{\kappa }_{t-1}\mathrm{,}t\ge 1\end{array}$

Specially, the market $M_0$ with $\kappa =0$ is the original market.

We consider the unconstraint optimal portfolio problem in the market $M_{\kappa }$ :

$\begin{array}{l}maxEU\left(V_T^{\kappa }\right)\\ \text{s}\text{.t}{V}_0=v\end{array}$

Let $J_{\kappa }\left(v\right)$ denote the corresponding optimal objective value in the market $M_{\kappa }$ .

Theorem 3.1. Suppose $J_0^{\mathrm{<mo>\; *\; </mo>}}$ is the optimal solution of the primal constrained problem, and $J^{\mathrm{<mo>\; *\; </mo>}}$ is the optimal solution of the dual problem

$\underset{\kappa \in \mathcal{N}}{min}{J}_{\kappa }\left(v\right)\mathrm{,}$

where $J_{\kappa }\left(v\right)$ is the optimal objective value in the unconstrained market $M_{\kappa }$ , associated with the optimal solution ${\kappa }^{\mathrm{<mo>\; *\; </mo>}}$ . If the optimal trading strategy $\pi$ for the unconstrained market $M_{{\kappa }^{\mathrm{<mo>\; *\; </mo>}}}$ satisfies.

a) $\pi \in \mathcal{A}$

b) ${{\pi }^{\prime }}_t{\kappa }_{t-1}^{*}=0$ , for all $t\ge 1$

Then $\pi$ is the optimal strategy for the original constrained market, and $J_0=J^{*}$ .

Proof. For the market $M_{{\kappa }^{\mathrm{<mo>\; *\; </mo>}}}$ and optimal trading strategy $\pi$ which satisfies (a) and (b), the value of portfolio at time $T$ is

$\begin{array}{c}{V}_T^{{\kappa }^{\mathrm{<mo>\; *\; </mo>}}}\left(\pi \right)=v{\displaystyle {\prod }_{t=1}^T\left[1+r_t+{{\pi }^{\prime }}_t\left(R_t+B_t{\kappa }_{t-1}^{\mathrm{<mo>\; *\; </mo>}}-r_{t}1\right)\right]}\\ =v{\displaystyle {\prod }_{t=1}^T\left[1+r_t+{{\pi }^{\prime }}_t\left(R_t-r_{t}1\right)+B_t{{\pi }^{\prime }}_t{\kappa }_{t-1}^{\mathrm{<mo>\; *\; </mo>}}\right]}\\ =v{\displaystyle {\prod }_{t=1}^T\left[1+r_t+{{\pi }^{\prime }}_t\left(R_t-r_{t}1\right)\right]}=V_T^0\left(\pi \right)\end{array}$

As $\pi$ is a feasible solution of the original constrained problem, the expected utility of $V_T^0\left(\pi \right)$ is smaller than or equal to the optimal value of the original constrained problem. So we have $J^{*}=EU\left(V_T^{{\kappa }^{*}}\right)=EU\left(V_T^0\right)\le J_0^{*}$ .

On the overhands, for an arbitrary market $M_{\kappa }$ and the optimal trading strategy ${\pi }^{\mathrm{<mo>\; *\; </mo>}}$ of the original constrained portfolio problem, we have,

$\begin{array}{c}{V}_T^{\kappa }\left({\pi }^{\mathrm{<mo>\; *\; </mo>}}\right)=v{\displaystyle {\prod }_{t=1}^T\left[1+r_t+{\pi }_t^{\mathrm{<mo>\; *\; </mo>}}{}^{\prime }\left(R_t+B_t{\kappa }_{t-1}-r_{t}1\right)\right]}\\ =v{\displaystyle {\prod }_{t=1}^T\left[1+r_t+{\pi }_t^{\mathrm{<mo>\; *\; </mo>}}{}^{\prime }\left(R_t-r_{t}1\right)+B_t{\pi }_t^{\mathrm{<mo>\; *\; </mo>}}{}^{\prime }{\kappa }_{t-1}\right]}\\ \ge {\displaystyle {\prod }_{t=1}^T\left[1+r_t+{\pi }_t^{\mathrm{<mo>\; *\; </mo>}}{}^{\prime }\left(R_t-r_{t}1\right)\right]}=V_T^0\left({\pi }^{\mathrm{<mo>\; *\; </mo>}}\right)\end{array}$

Since $EU\left(V_T^{{\kappa }^{*}}\left({\pi }^{*}\right)\right)\le EU\left(V_T^{{\kappa }^{*}}\left(\pi \right)\right)=J_{{\kappa }^{*}}\left(v\right)\le J_{\kappa }\left(v\right)$ for any $\kappa$ , therefore, $J_0^{*}=EU\left(V_T^0\left({\pi }^{*}\right)\right)\le EU\left(V_T^{{\kappa }^{*}}\left({\pi }^{*}\right)\right)\le J_{\kappa }\left(v\right)$ for any $\kappa$ . Hence, $J_0^{*}\le J_{{\kappa }^{*}}\left(v\right)=J^{*}$ .

Putting together the above two inequalities, we have $J^{*}=J_0^{*}$ .

4. Martingale Method

Now we try to solve the auxiliary problems

$\begin{array}{l}\max EU\left(V_T^{\kappa }\right)\\ \text{s}\text{.t}{V}_0=v\end{array}$

Denote the risk neutral probability in the market $M_{\kappa }$ as $Q_{\kappa }$ . Let $L\left(\omega \right)=Q\left(\omega \right)/P\left(\omega \right)$ be the state price density.

Proposition 4.1. Under the no-arbitrage consideration, The expected dis- counted terminal wealth based on the risk neutral probability is equal to the initial wealth, i.e.

$E_{Q_{\kappa }}\left(V_T^{\kappa }/B_T^{\kappa }\right)=v.$

So the problem is equivalent to

$\begin{array}{l}\max EU\left(V_T^{\kappa }\right)\\ \text{s}\text{.t}{E}_{Q_{\kappa }}\left(V_T^{\kappa }/B_T^{\kappa }\right)=v\end{array}$

Theorem 4.1. For the above optimal problem with quadratic utility function, the optimal attainable wealth is:

$V_T^{\kappa *}=\beta +\left[\frac{v-\beta E\left[L^{\kappa }/B_T^{\kappa }\right]}{E\left[{\left(L^{\kappa }\right)}^2/{\left(B_T^{\kappa }\right)}^2\right]}\right]L^{\kappa }/B_T^{\kappa },$

and the optimal objective value is

$EU\left(V_T^{\kappa *}\right)=\frac{1}{2}{\beta }^2-\frac{{\left(v-\beta E\left[L^{\kappa }/B_T^{\kappa }\right]\right)}^2}{2E\left[{\left(L^{\kappa }\right)}^2/{\left(B_T^{\kappa }\right)}^2\right]}.$

Proof.

$\begin{array}{l}EU\left(V_T^{\kappa }\right)-\lambda E_{Q_{\kappa }}\left(V_T^{\kappa }\right)\\ =EU\left(V_T^{\kappa }\right)-\lambda E\left(V_T^{\kappa }L/B_T\right)\\ ={\displaystyle \underset{i=1}{\overset{{\left(n+1\right)}^T}{\sum }}}P\left({\omega }_i\right)\left[U\left(V_T^{\kappa }\left({\omega }_i\right)\right)-\lambda V_T^{\kappa }\left({\omega }_i\right)L\left({\omega }_i\right)/B_T\right]\end{array}$

The necessary conditions to maximize this expression must be:

$U^{\prime }\left(V_T^{\kappa }\left(\omega \right)\right)=\lambda L\left(\omega \right)/B_T,\mathrm{<mi>\; </mi>\; <mi>\; </mi>}\text{for}\text{all}\omega \in \Omega .$

This is equivalent to

$V_T^{\kappa }\left(\omega \right)=I\left(\lambda L\left(\omega \right)/B_T\right)=\beta -\lambda L\left(\omega \right)/B_T,\mathrm{<mi>\; </mi>\; <mi>\; </mi>}\text{for}\text{all}\omega \in \Omega .$

The value of the parameter $\lambda$ is the one that makes $V_T^{\kappa }$ satisfies $E_{Q_{\kappa }}\left(V_T^{\kappa \mathrm{<mo>\; *\; </mo>}}\right)=v$ . Hence

$E_{Q_{\kappa }}\left(\left(\beta -\lambda L/B_T\right)/B_T\right)=E\left(\left(\beta -\lambda L/B_T\right)L/B_T\right)=\beta E\left(L/B_T\right)-\lambda E\left(L^2/B_T^2\right)=v$

Therefore, $\lambda =\left[\beta E\left(L/B_T\right)-v\right]/E\left(L^2/B_T^2\right)$ . Hence, we have

$V_T^{\kappa *}=\beta +\left[\frac{v-\beta E\left[L/B_T\right]}{E\left[L^2/B_T^2\right]}\right]L/B_T,\mathrm{<mi>\; </mi>\; <mi>\; </mi>}\text{all}\omega \in \Omega ,$

and the optimal objective value

$J_{\kappa }\left(v\right)=\frac{1}{2}{\beta }^2-\frac{{\left(v-\beta E\left[L/B_T\right]\right)}^2}{2E\left[L^2/B_T^2\right]}.$

5. Optimal Terminal Wealth

Now we come to the dual problem:

$\underset{\kappa \in \mathcal{N}}{min}{J}_{\kappa }\left(v\right)=\frac{1}{2}{\beta }^2-\frac{{\left(v-\beta E\left[L/B_T\right]\right)}^2}{2E\left[L^2/B_T^2\right]}\mathrm{.}$

Since $E\left[L/B_T\right]=E\left[L\right]/B_T=1/B_T$ and $E\left[L^2/B_T^2\right]=E\left[L^2\right]/B_T^2$ , the problem is equivalent to

$\underset{\kappa \in \mathcal{N}}{min}E\left[L^2\right]={\displaystyle \underset{i=1}{\overset{{\left(n+1\right)}^T}{\sum }}}{Q}^2\left({\omega }_i\right).$

Definition 5.1. For arbitrary ${\omega }_i=\left\{e_1^i,\cdots ,e_T^i\right\}\in \Omega$ , we defined the matrix of the price change at time $t$ as

$D_t^{e_{t-1}^i}=\left(\begin{array}{cccc}{\delta }_t\left(1,e_{t-1}^i\right)& {\delta }_t\left(1,e_{t-1}^i+1\right)& \cdots & {\delta }_t\left(1,e_{t-1}^i+n\right)\\ ⋮& ⋮& \ddots & ⋮\\ {\delta }_t\left(n,e_{t-1}^i\right)& {\delta }_t\left(n,e_{t-1}^i+1\right)& \cdots & {\delta }_t\left(n,e_{t-1}^i+n\right)\end{array}\right),$

where ${\delta }_t\left(j\mathrm{,}i\right)$ is the change of discounted price of jth security at time $t$ when the market is at state $i\in K\left(t-1\right)$ at time $t-1$ .

Definition 5.2. Denote $D_t^{e_{t-1}^i}\left(j\right)$ as an $n\times n$ matrix, which comes from $D_t^{e_{t-1}^i}$ by deleting column $j$ .

Definition 5.3. Denote ${\tilde{D}}_t^{e_{t-1}^i}\left(l\mathrm{,}j\right)$ as an $n\times n$ matrix, which comes from $D_t^{e_{t-1}^i}\left(l\right)$ by replacing the row $j$ with $1_{1\times n}$ .

Theorem 5.1. Under the assumption 2.1, the market exists an unique risk neutral probability

$Q\left({\omega }_i\right)={\displaystyle \underset{t=1}{\overset{T}{\prod }}}\frac{{\left(-1\right)}^{e_t^i}\left[\left|D_t^{e_{t-1}^i}\left(e_t^i\right)\right|+{{\displaystyle \sum }}_{j=1}^n\left|{\tilde{D}}_t^{e_{t-1}^i}\left(e_t^i,j\right)\right|S_{t-1}\left(j,e_{t-1}^i\right){\kappa }_{t-1}\left(j,e_{t-1}^i\right)\right]}{{{\displaystyle \sum }}_{j=1}^{n+1}{\left(-1\right)}^j\left|D_t^{e_{t-1}^i}\left(j\right)\right|},$

$S_t\left(i\mathrm{,}j\right)$ is the price of the ith risky security at time $t$ when the market is at the state $j\in K\left(t\right)$ .

Proof. We can see that $Q\left({\omega }_i\right)>0$ for any $i=1,2,\cdots ,{\left(n+1\right)}^T$ . First, we try to prove that the sum of $Q\left({\omega }_i\right)$ is equal to one.

For $T=1$ , we have

$Q\left({\omega }_i\right)=\frac{{\left(-1\right)}^{e_1^i}\left[\left|D_1^1\left(e_1^i\right)\right|+{{\displaystyle \sum }}_{j=1}^n\left|{\tilde{D}}_1^1\left(e_1^i,j\right)\right|S_0\left(j\right){\kappa }_0\left(j\right)\right]}{{{\displaystyle \sum }}_{j=1}^{n+1}{\left(-1\right)}^j\left|D_1^1\left(j\right)\right|},$

and $e^i\left(1\right)=i$ .

${\displaystyle \underset{i}{\sum }}Q\left({\omega }_i\right)=\frac{{{\displaystyle \sum }}_{j=1}^{n+1}{\left(-1\right)}^i\left|D_1^1\left(i\right)\right|+{{\displaystyle \sum }}_{j=1}^{n+1}{\left(-1\right)}^i{{\displaystyle \sum }}_{j=1}^n\left|{\tilde{D}}_1^1\left(i,j\right)\right|S_0\left(j\right){\kappa }_0\left(j\right)}{{{\displaystyle \sum }}_{j=1}^{n+1}{\left(-1\right)}^j\left|D_1^1\left(j\right)\right|}.$

Because

$\begin{array}{l}{\displaystyle \underset{i=1}{\overset{n+1}{\sum }}}{\left(-1\right)}^i{\displaystyle \underset{j=1}{\overset{n}{\sum }}}\left|{\tilde{D}}_1^1\left(i,j\right)\right|S_0\left(j\right){\kappa }_0\left(j\right)={\displaystyle \underset{j=1}{\overset{n}{\sum }}}\left[{\displaystyle \underset{i=1}{\overset{n+1}{\sum }}}{\left(-1\right)}^i\left|{\tilde{D}}_1^1\left(i,j\right)\right|S_0\left(j\right){\kappa }_0\left(j\right)\right]\\ ={\displaystyle \underset{j=1}{\overset{n}{\sum }}}\left[\left(-1\right)\left|{\tilde{D}}_1^1\left(1,j\right)\right|+\left|{\tilde{D}}_1^1\left(2,j\right)\right|+\cdots +{\left(-1\right)}^{n+1}\left|{\tilde{D}}_1^1\left(n+1,j\right)\right|\right]S_0\left(j\right){\kappa }_0\left(j\right)\\ ={\displaystyle \underset{j+1}{\overset{n}{\sum }}}\left|A_1\left(j\right)\right|S_0\left(j\right){\kappa }_0\left(j\right)=0,\end{array}$

where

$A_t\left(j\right)={\left(\begin{array}{cccc}1& 1& \cdots & 1\\ {\delta }_t\left(\mathrm{1,1}\right)& {\delta }_t\left(\mathrm{1,2}\right)& \cdots & {\delta }_t\left(\mathrm{1,1}+n\right)\\ ⋮& ⋮& \ddots & ⋮\\ {\delta }_t\left(j-\mathrm{1,1}\right)& {\delta }_t\left(j-\mathrm{1,2}\right)& \cdots & {\delta }_t\left(j-\mathrm{1,1}+n\right)\\ 1& 1& \ddots & 1\\ {\delta }_t\left(j+\mathrm{1,1}\right)& {\delta }_t\left(j+\mathrm{1,2}\right)& \cdots & {\delta }_t\left(j+\mathrm{1,1}+n\right)\\ ⋮& ⋮& \ddots & ⋮\\ {\delta }_t\left(n\mathrm{,1}\right)& {\delta }_t\left(n\mathrm{,2}\right)& \cdots & {\delta }_t\left(n\mathrm{,1}+n\right)\end{array}\right)}_{\left(n+1\right)\times \left(n+1\right)}\mathrm{,}$

hence

${\displaystyle \underset{i}{\sum }}Q\left({\omega }_i\right)=\frac{{{\displaystyle \sum }}_{i=1}^{n+1}{\left(-1\right)}^i\left|D_1^1\left(i\right)\right|}{{{\displaystyle \sum }}_{j=1}^{n+1}{\left(-1\right)}^j\left|D_1^1\left(j\right)\right|}=1.$

Suppose for $T=k$ , the sum of the $Q_k\left({\omega }_i\right)$ $\left(i=1,2,\cdots ,{\left(n+1\right)}^k\right)$ is one.For $T=k+1$ , the sample space is ${\Omega }_{k+1}$ . Under the assumption 2.1, ${\Omega }_{k+1}$ can be divided into ${\left(n+1\right)}^k$ subspace ${\Omega }_{k+1}={\Omega }_{k+1}^1\cup {\Omega }_{k+1}^2\cup \cdots \cup {\Omega }_{k+1}^{{\left(n+1\right)}^k}$ , where ${\Omega }_{k+1}^l$ includes all the $\omega$ which has the same state in the first k period (i.e. $\left(e_1^l\mathrm{,}\cdots \mathrm{,}{e}_k^l\right)={\tilde{\omega }}_l$ ), and $e_{k+1}\in {\bar{K}}^{e_k^l}\left(k+1\right)=\left\{e_k^l,e_k^l+1,\cdots ,e_k^l+n\right\}$ . ${\Omega }_{k+1}^i\cap {\Omega }_{k+1}^j=\varnothing$ for any $i\ne j$ . So for arbitrary subspace ${\Omega }_{k+1}^l$ ,

$\begin{array}{l}{\displaystyle \underset{{\omega }_i\in {\Omega }_{k+1}^l}{\sum }}{Q}_{k+1}\left({\omega }_i\right)\\ ={\displaystyle \underset{{\omega }_i\in {\Omega }_{k+1}^l}{\sum }}{\displaystyle \underset{t=1}{\overset{k+1}{\prod }}}\frac{{\left(-1\right)}^{e_t^i}\left[\left|D_t^{e_{t-1}^i}\left(e_t^i\right)\right|+{{\displaystyle \sum }}_{j=1}^n\left|{\tilde{D}}_t^{e_{t-1}^i}\left(e_t^i,j\right)\right|S_{t-1}\left(j,e_{t-1}^i\right){\kappa }_{t-1}\left(j,e_{t-1}^i\right)\right]}{{{\displaystyle \sum }}_{j=1}^{n+1}{\left(-1\right)}^j\left|D_t^{e_{t-1}^i}\left(j\right)\right|}\text{}\\ ={\displaystyle \underset{t=1}{\overset{k}{\prod }}}\frac{{\left(-1\right)}^{e_t^i}\left[\left|D_t^{e_{t-1}^i}\left(e_t^i\right)\right|+{{\displaystyle \sum }}_{j=1}^n\left|{\tilde{D}}_t^{e_{t-1}^i}\left(e_t^i,j\right)\right|S_{t-1}\left(j,e_{t-1}^i\right){\kappa }_{t-1}\left(j,e_{t-1}^i\right)\right]}{{{\displaystyle \sum }}_{j=1}^{n+1}{\left(-1\right)}^j\left|D_t^{e_{t-1}^i}\left(j\right)\right|}\\ \times {\displaystyle \underset{{\omega }_i\in {\Omega }_{k+1}^l}{\sum }}\frac{{\left(-1\right)}^{e_{k+1}^i}\left[\left|D_{k+1}^{e_k^i}\left(e_{k+1}^i\right)\right|+{{\displaystyle \sum }}_{j=1}^n\left|{\tilde{D}}_t^{e_k^i}\left(e_{k+1}^i,j\right)\right|S_k\left(j,e_k^i\right){\kappa }_k\left(j,e_k^i\right)\right]}{{{\displaystyle \sum }}_{j=1}^{n+1}{\left(-1\right)}^j\left|D_{k+1}^{e_k^i}\left(j\right)\right|}\\ ={\displaystyle \underset{t=1}{\overset{k}{\prod }}}\frac{{\left(-1\right)}^{e_t^i}\left[\left|D_t^{e_{t-1}^i}\left(e_t^i\right)\right|+{{\displaystyle \sum }}_{j=1}^n\left|{\tilde{D}}_t^{e_{t-1}^i}\left(e_t^i,j\right)\right|S_{t-1}\left(j,e_{t-1}^i\right){\kappa }_{t-1}\left(j,e_{t-1}^i\right)\right]}{{{\displaystyle \sum }}_{j=1}^{n+1}{\left(-1\right)}^j\left|D_t^{e_{t-1}^i}\left(j\right)\right|}\end{array}$

we can verify that

${\displaystyle \underset{{\omega }_i\in {\Omega }_{k+1}^l}{\sum }}{Q}_{k+1}\left({\omega }_i\right)=Q_k\left({\tilde{\omega }}_l\right).$

Therefore,

${\displaystyle \underset{i=1}{\overset{{\left(n+1\right)}^{k+1}}{\sum }}}{Q}_{k+1}\left({\omega }_i\right)={\displaystyle \underset{l=1}{\overset{{\left(n+1\right)}^k}{\sum }}}\left({\displaystyle \underset{{\omega }_i\in {\Omega }_{k+1}^l}{\sum }}{Q}_{k+1}\left({\omega }_i\right)\right)={\displaystyle \underset{l=1}{\overset{{\left(n+1\right)}^k}{\sum }}}{Q}_k\left({\tilde{\omega }}_l\right)=1.$

So we conclude that for any T, the sum of $Q\left({\omega }_i\right)$ is one, and this defines a probability.

Now we try to prove that the probability is a risk neutral probability in the market. Consider an arbitrary time t, and arbitrary event A corresponding to ${\mathcal{F}}_{t-1}$ (i.e. for $\omega \in A$ , $\left(e_1\mathrm{,}\cdots \mathrm{,}{e}_{t-1}\right)=\tilde{\omega }$ have been known). Suppose $e_{t-1}=\zeta$ , we know that $\forall \omega \in A$ , $e_t\in {\bar{K}}^{\zeta }\left(t\right)=\left\{\zeta ,\zeta +1,\cdots ,\zeta +n\right\}$ . We denote the subset of A as $A^1\mathrm{,}\cdots \mathrm{,}{A}^{n+1}$ , where all element in $A^i$ has $e_t=\zeta +i-1$ ( $A=A^1\cup A^2\cdots \cup A^{n+1}$ ). For ith $\left(i=1,\cdots ,n\right)$ risky security we have

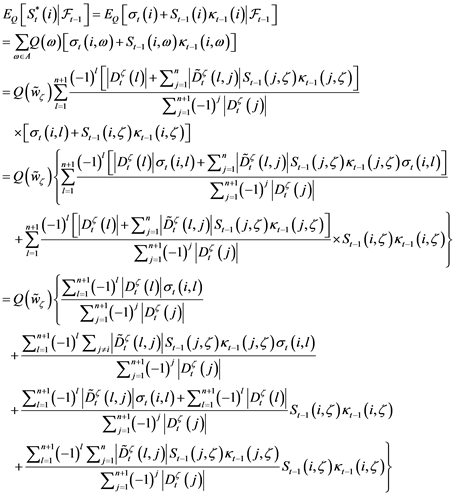
There are four part. For part (1),

${\displaystyle \underset{l=1}{\overset{n+1}{\sum }}}{\left(-1\right)}^l\left|D_t^{\zeta }\left(l\right)\right|{\sigma }_t\left(i,l\right)=-\left|\left(\begin{array}{c}{C}_t^{\zeta }\\ D_t^{\zeta }\end{array}\right)\right|=0,$

where $C_t^{\zeta }$ is the ith row of $D_t^{\zeta }$ .

For part (2), because

$\begin{array}{l}{\displaystyle \underset{l=1}{\overset{n+1}{\sum }}}{\left(-1\right)}^l\left|{\tilde{D}}_t^{\zeta }\left(l,j\right)\right|S_{t-1}\left(j,\zeta \right){\kappa }_{t-1}\left(j,\zeta \right){\sigma }_t\left(i,l\right)\\ =-\left|\left(\begin{array}{c}{C}_t^{\zeta }\\ {\tilde{D}}_t^{\zeta }\left(l,j\right)\end{array}\right)\right|S_{t-1}\left(j,\zeta \right){\kappa }_{t-1}\left(j,\zeta \right)=0\end{array}$

for $j\ne i$ , where $C_t^{\zeta }$ is the ith row of $D_t^{\zeta }$ . Hence,

${\displaystyle \underset{l\mathrm{<mo>\; =\; </mo>1}}{\overset{n+1}{\sum }}}{\displaystyle \underset{j\ne i}{\sum }}{\left(-1\right)}^l\left|{\tilde{D}}_t^{\zeta }\left(l\mathrm{,}j\right)\right|S_{t-1}\left(j\mathrm{,}\zeta \right){\kappa }_{t-1}\left(j\mathrm{,}\zeta \right){\sigma }_t\left(i\mathrm{,}l\right)=0.$

For part (3),

$\begin{array}{l}{\displaystyle \underset{l=1}{\overset{n+1}{\sum }}}{\left(-1\right)}^l\left|{\tilde{D}}_t^{\zeta }\left(l,i\right)\right|{\sigma }_t\left(i,l\right)+{\displaystyle \underset{l=1}{\overset{n+1}{\sum }}}{\left(-1\right)}^l\left|D_t^{\zeta }\left(l\right)\right|\\ =\left(-1\right)\left|\left(\begin{array}{c}{C}_t^{\zeta }\\ {\tilde{D}}_t^{\zeta }\left(l,i\right)\end{array}\right)\right|+\left(-1\right)\left|\left(\begin{array}{c}{1}_{1\times n}\\ D_t^{\zeta }\left(l\right)\end{array}\right)\right|\\ =\left(-1\right)\left|\left(\begin{array}{c}{C}_t^{\zeta }\\ {\tilde{D}}_t^{\zeta }\left(l,i\right)\end{array}\right)\right|+{\left(-1\right)}^2\left|\left(\begin{array}{c}{C}_t^{\zeta }\\ {\tilde{D}}_t^{\zeta }\left(l,i\right)\end{array}\right)\right|=0\end{array}$

For part (4),

$\begin{array}{l}{\displaystyle \underset{l=1}{\overset{n+1}{\sum }}}{\left(-1\right)}^l{\displaystyle \underset{j=1}{\overset{n}{\sum }}}\left|{\tilde{D}}_t^{\zeta }\left(l,j\right)\right|S_{t-1}\left(j,\zeta \right){\kappa }_{t-1}\left(j,\zeta \right)\\ ={\displaystyle \underset{j=1}{\overset{n}{\sum }}}\left|A_t\left(j\right)\right|S_{t-1}\left(j,\zeta \right){\kappa }_{t-1}\left(j,\zeta \right)=0.\end{array}$

Hence,

$E_Q\left[{\sigma }_t\left(i\right)+S_{t-1}\left(i\right){\kappa }_{t-1}\left(i\right)|{\mathcal{F}}_{t-1}\right]=\mathrm{0,\; <mi>\; </mi>\; <mi>\; </mi>}\forall i\mathrm{,\; <mi>\; </mi>}t\mathrm{.}$

So this probability is a risk neutral probability of the market.

The dual problem is equivalent to

$\underset{\kappa \in \mathcal{N}}{\min }{\displaystyle \underset{i}{\sum }}{\displaystyle \underset{t=1}{\overset{T}{\prod }}}{\left[\left|D_t^{e_{t-1}^i}\left(e_t^i\right)\right|+{\displaystyle \underset{j=1}{\overset{n}{\sum }}}\left|{\tilde{D}}_t^{e_{t-1}^i}\left(e_t^i,j\right)\right|S_{t-1}\left(j,e_{t-1}^i\right){\kappa }_{t-1}\left(j,e_{t-1}^i\right)\right]}^2.$

To simplify our problem, we give the following notations:

$a_t^l\left(i\right)=\left|D_t^l\left(i\right)\right|,$

${\kappa }_{t-1}\left(l\right)={\left({\kappa }_{t-1}\left(1,l\right),\cdots ,{\kappa }_{t-1}\left(n,l\right)\right)}^{\prime },$

$b_t^l\left(i,j\right)=\left|{\tilde{D}}_t^l\left(i,j\right)\right|S_{t-1}\left(j,l\right),$

$b_t^l\left(i\right)={\left(b_t^l\left(i,1\right),\cdots ,b_t^l\left(i,n\right)\right)}^{\prime }.$

So the problem can be rewrite as:

$\underset{\kappa \in \mathcal{N}}{\min }{\displaystyle \underset{i}{\sum }}{\displaystyle \underset{t=1}{\overset{T}{\prod }}}{\left[a_t^{e_{t-1}^i}\left(e_t^i\right)+b_t^{e_{t-1}^i}{\left(e_t^i\right)}^{\prime }{\kappa }_{t-1}\left(e_{t-1}^i\right)\right]}^2$

There have some special properties of the objective function, which makes the calculus much easy. Denote

${\phi }_{\tau }\left(i\right)={\displaystyle \underset{\left\{\left(e_{\tau },\cdots ,e_T\right);e_{\tau }=i\in K\left(\tau \right)\right\}}{\sum }}{\displaystyle \underset{t=\tau }{\overset{T}{\prod }}}{\left[a_{t+1}^{e_t}\left(e_{t+1}\right)+b_{t+1}^{e_t}{\left(e_{t+1}\right)}^{\prime }{\kappa }_t\left(e_t\right)\right]}^2.$

Proposition 5.1. Under the assumption 2.1, ${\phi }_{\tau }\left(i\right)$ have the following pro- perty:

$\begin{array}{c}{\phi }_{\tau -1}\left(l\right)={\displaystyle \underset{\left\{\left(e_{\tau -1},e_{\tau },\cdots ,e_T\right);e_{\tau -1}=l\in K\left(\tau -1\right)\right\}}{\sum }}{\displaystyle \underset{t=\tau -1}{\overset{T}{\prod }}}{\left[a_{t+1}^{e_t}\left(e_{t+1}\right)+b_{t+1}^{e_t}{\left(e_{t+1}\right)}^{\prime }{\kappa }_t\left(e_t\right)\right]}^2\\ ={\displaystyle \underset{i=l}{\overset{l+n}{\sum }}}{\displaystyle \underset{\left\{\left(e_{\tau -1},e_{\tau },\cdots ,e_T\right);e_{\tau -1}=l\in K\left(\tau -1\right),e_{\tau }=i\in K\left(\tau \right)\right\}}{\sum }}{\displaystyle \underset{t=\tau -1}{\overset{T}{\prod }}}{\left[a_{t+1}^{e_t}\left(e_{t+1}\right)+b_{t+1}^{e_t}{\left(e_{t+1}\right)}^{\prime }{\kappa }_t\left(e_t\right)\right]}^2\\ ={\displaystyle \underset{i=l}{\overset{l+n}{\sum }}}{\left[a_{\tau }^l\left(i\right)+b_{\tau }^l{\left(i\right)}^{\prime }{\kappa }_{\tau -1}\left(l\right)\right]}^2{\phi }_{\tau }\left(i\right)\end{array}$

So we have

$\begin{array}{l}{f}_0:={\displaystyle \underset{i}{\sum }}{\displaystyle \underset{t=1}{\overset{T}{\prod }}}{\left[a_t^{e_{t-1}^i}\left(e_t^i\right)+b_t^{e_{t-1}^i}{\left(e_t^i\right)}^{\prime }{\kappa }_{t-1}\left(e_{t-1}^i\right)\right]}^2\\ ={\displaystyle \underset{l_1\in K\left(1\right)}{\sum }}{\left[a_1^1\left(l_1\right)+b_1^1{\left(l_1\right)}^{\prime }{\kappa }_0\left(1\right)\right]}^2\{{\displaystyle \underset{l_2\in K\left(2\right)}{\sum }}{\left[a_2^{l_1}\left(l_2\right)+b_2^{l_1}{\left(l_2\right)}^{\prime }{\kappa }_1\left(l_1\right)\right]}^2\\ \left\{{\displaystyle \underset{l_3\in K\left(3\right)}{\sum }}\cdots \left\{{\displaystyle \underset{l_T\in K\left(T\right)}{\sum }}{\left[a_T^{l_{T-1}}\left(l_T\right)+b_T^{l_{T-1}}{\left(l_T\right)}^{\prime }{\kappa }_{T-1}\left(l_{T-1}\right)\right]}^2\right\}\right\}\}.\end{array}$

The problem is separable and can be solved by dynamic programming.

Theorem 5.2. If $\left[{\displaystyle {\sum }_{i=m}^{m+n}}{\phi }_{t+1}\left(i\right)\cdot b_{t+1}^m\left(i\right)b_{t+1}^m{\left(i\right)}^{\prime }\right]$ has full rank for any $t$ and $m\in K\left(t\right)$ , then the optimal solution of the dual problem is

${\kappa }_t^{\mathrm{<mo>\; *\; </mo>}}\left(m\right)={\left({\kappa }_t^{\mathrm{<mo>\; *\; </mo>}}\left(\mathrm{1,}m\right)\mathrm{,}\cdots \mathrm{,}{\kappa }_t^{\mathrm{<mo>\; *\; </mo>}}\left(n\mathrm{,}m\right)\right)}^{\prime }$

for $t=0,1,2,\cdots ,T-1$ and $m=1,2,\cdots ,nt+1$ , with

${\kappa }_t^{\mathrm{<mo>\; *\; </mo>}}\left(j\mathrm{,}m\right)=\{\begin{array}{l}{\tilde{\kappa }}_t\left(j\mathrm{,}m\right)\text{if}{\tilde{\kappa }}_t\left(j\mathrm{,}m\right)\ge 0\\ 0\text{if}{\tilde{\kappa }}_{\tau -1}\left(j\mathrm{,}m\right)<0\end{array}$

where ${\tilde{\kappa }}_t\left(m\right)={\left({\tilde{\kappa }}_t\left(\mathrm{1,}m\right)\mathrm{,}\cdots \mathrm{,}{\tilde{\kappa }}_t\left(n\mathrm{,}m\right)\right)}^{\prime }$ is:

${\tilde{\kappa }}_t\left(m\right)=-{\left[{\displaystyle \underset{i=m}{\overset{m+n}{\sum }}}{\phi }_{t+1}\left(i\right)\cdot b_{t+1}^m\left(i\right)b_{t+1}^m{\left(i\right)}^{\prime }\right]}^{-1}\cdot \left[{\displaystyle \underset{i=m}{\overset{m+n}{\sum }}}{\phi }_{t+1}\left(i\right)\cdot b_{t+1}^m\left(i\right)\cdot a_{t+1}^m\left(i\right)\right],$

${\phi }_{t+1}\left(m\right)={\displaystyle \underset{i=m}{\overset{m+n}{\sum }}}{\left[a_{t+2}^m\left(i\right)+b_{t+2}^m{\left(i\right)}^{\prime }{\kappa }_{t+1}^{*}\left(m\right)\right]}^2{\phi }_{t+2}\left(i\right).$

Proof. Let

$\begin{array}{l}{f}_{t-1}\left(l_{t-1}\right):={\displaystyle \underset{l_t\in K^{l_{t-1}}\left(t\right)}{\sum }}{\left[a_t^{l_{t-1}}\left(l_t\right)+b_t^{l_{t-1}}{\left(l_t\right)}^{\prime }{\kappa }_{t-1}\left(l_{t-1}\right)\right]}^2\{{\displaystyle \underset{l_{t+1}\in K^{l_t}\left(t+1\right)}{\sum }}\cdots \\ \left\{{\displaystyle \underset{l_T\in K^{l_{T-1}}\left(T\right)}{\sum }}{\left[a_T^{l_{T-1}}\left(l_T\right)+b_T^{l_{T-1}}{\left(l_T\right)}^{\prime }{\kappa }_{T-1}\left(l_{T-1}\right)\right]}^2\right\}\}\\ ={\displaystyle \underset{l_t\in K^{l_{t-1}}\left(t\right)}{\sum }}{\left[a_t^{l_{t-1}}\left(l_t\right)+b_t^{l_{t-1}}{\left(l_t\right)}^{\prime }{\kappa }_{t-1}\left(l_{t-1}\right)\right]}^2{f}_t\left(l_t\right)\end{array}$

At $s=T-1$ , for $l_{T-1}\in K\left(T-1\right)=\left\{1,2,\cdots ,n\left(T-1\right)+1\right\}$ ,

$f_{T-1}\left(l_{T-1}\right)={\displaystyle \underset{l_T\in K^{l_{T-1}}\left(T\right)}{\sum }}{\left[a_T^{l_{T-1}}\left(l_T\right)+b_T^{l_{T-1}}{\left(l_T\right)}^{\prime }{\kappa }_{T-1}\left(l_{T-1}\right)\right]}^2.$

We separately solve the following problem for each $l_{T-1}=m$ :

$\begin{array}{l}max{{\displaystyle \sum }}_{i=m}^{m+n}{\left[a_T^m\left(i\right)+b_T^m{\left(i\right)}^{\prime }{\kappa }_{T-1}\left(m\right)\right]}^2\\ \text{s}\text{.t}{\kappa }_{T-1}\left(m\right)\ge 0\end{array}$

We solve the unconstrained problem, and the optimal ${\tilde{\kappa }}_{T-1}\left(m\right)={\left({\tilde{\kappa }}_{T-1}\left(\mathrm{1,}m\right)\mathrm{,}\cdots \mathrm{,}{\tilde{\kappa }}_{T-1}\left(n\mathrm{,}m\right)\right)}^{\prime }$ is:

${\tilde{\kappa }}_{T-1}\left(m\right)=-{\left[{\displaystyle \underset{i=m}{\overset{m+n}{\sum }}}{b}_T^m\left(i\right)\cdot b_T^m{\left(i\right)}^{\prime }\right]}^{-1}\cdot \left[{\displaystyle \underset{i=m}{\overset{m+n}{\sum }}}{b}_T^m\left(i\right)\cdot a_T^m\left(i\right)\right]$

The optimal solution of the constrained problem is ${\kappa }_{T-1}\left(m\right)={\left({\kappa }_{T-1}\left(1,m\right),\cdots ,{\kappa }_{T-1}\left(n,m\right)\right)}^{\prime }$ where

${\kappa }_{T-1}^{\mathrm{<mo>\; *\; </mo>}}\left(j\mathrm{,}m\right)=\{\begin{array}{ll}{\tilde{\kappa }}_{T-1}\left(j,m\right)\hfill & \text{if}{\tilde{\kappa }}_{T-1}\left(j,m\right)\ge 0\hfill \\ 0\hfill & \text{if}{\tilde{\kappa }}_{T-1}\left(j,m\right)<0\hfill \end{array}$

So $f_{T-1}\left(m\right)={\phi }_{T-1}\left(m\right)={\displaystyle {\sum }_{i=m}^{m+n}}{\left[a_T^m\left(i\right)+b_T^m{\left(i\right)}^{\prime }{\kappa }_{T-1}^{*}\left(m\right)\right]}^2$ , and

$f_{T-2}\left(l_{T-2}\right)={\displaystyle \underset{l_{T-1}\in K^{l_{T-2}}\left(T-1\right)}{\sum }}{\left[a_{T-1}^{l_{T-2}}\left(l_{T-1}\right)+b_{T-1}^{l_{T-2}}{\left(l_{T-1}\right)}^{\prime }{\kappa }_{T-2}\left(l_{T-2}\right)\right]}^2{\phi }_{T-1}\left(l_{T-1}\right).$

Now we come to $s=T-2$ . We separably to solve the following problem for $l_{T-2}=m$ :

$\begin{array}{l}max{\displaystyle \underset{i=m}{\overset{m+n}{\sum }}}{\left[a_{T-1}^m\left(i\right)+b_{T-1}^m{\left(i\right)}^{\prime }{\kappa }_{T-2}\left(m\right)\right]}^2{\phi }_{T-1}\left(i\right)\\ \text{s}\text{.t}{\kappa }_{T-2}\left(m\right)\ge 0\end{array}$

We solve the unconstrained problem, and the optimal ${\tilde{\kappa }}_{T-2}\left(m\right)={\left({\tilde{\kappa }}_{T-2}\left(1,m\right),\cdots ,{\tilde{\kappa }}_{T-2}\left(n,m\right)\right)}^{\prime }$ is:

${\tilde{\kappa }}_{T-2}\left(m\right)=-{\left[{\displaystyle \underset{i=m}{\overset{m+n}{\sum }}}{b}_{T-1}^m\left(i\right)\cdot b_{T-1}^m{\left(i\right)}^{\prime }{\phi }_{T-1}\left(i\right)\right]}^{-1}\cdot \left[{\displaystyle \underset{i=m}{\overset{m+n}{\sum }}}{b}_{T-1}^m\left(i\right)\cdot a_{T-1}^m\left(i\right){\phi }_{T-1}\left(i\right)\right]$

The optimal solution of the constrained problem is ${\kappa }_{T-2}\left(m\right)={\left({\kappa }_{T-2}\left(\mathrm{1,}m\right)\mathrm{,}\cdots \mathrm{,}{\kappa }_{T-2}\left(n\mathrm{,}m\right)\right)}^{\prime }$ where

${\kappa }_{T-2}^{*}\left(j,m\right)=\{\begin{array}{ll}{\tilde{\kappa }}_{T-2}\left(j,m\right)\hfill & \text{if}{\tilde{\kappa }}_{T-2}\left(j,m\right)\ge 0\hfill \\ 0\hfill & \text{if}{\tilde{\kappa }}_{T-2}\left(j,m\right)<0\hfill \end{array}$

So $f_{T-2}\left(m\right)={\phi }_{T-2}\left(m\right)={\displaystyle {\sum }_{i=m}^{m+n}}{\left[a_{T-1}^m\left(i\right)+b_{T-1}^m{\left(i\right)}^{\prime }{\kappa }_{T-2}^{*}\left(m\right)\right]}^2{\phi }_{T-1}\left(i\right)$ , and

$f_{T-3}\left(l_{T-3}\right)={\displaystyle \underset{l_{T-2}\in K^{l_{T-3}}\left(T-2\right)}{\sum }}{\left[a_{T-2}^{l_{T-3}}\left(l_{T-2}\right)+b_{T-2}^{l_{T-3}}{\left(l_{T-2}\right)}^{\prime }{\kappa }_{T-3}\left(l_{T-3}\right)\right]}^2\times {\phi }_{T-2}\left(l_{T-2}\right).$

Generally, at stage $s=\tau$ , we suppose is

$f_{\tau }\left(l_{\tau }\right)={\displaystyle \underset{l_{\tau +1}\in K^{l_{\tau }}\left(\tau +1\right)}{\sum }}{\left[a_{\tau +1}^{l_{\tau }}\left(l_{\tau +1}\right)+b_{\tau +1}^{l_{\tau }}{\left(l_{\tau +1}\right)}^{\prime }{\kappa }_{\tau }\left(l_{\tau }\right)\right]}^2{\phi }_{\tau +1}\left(l_{\tau +1}\right)$

We separably to solve the following problem for each $l_{\tau }=m\in K\left(\tau \right)$ :

$\begin{array}{l}max{{\displaystyle \sum }}_{i=m}^{m+n}{\left[a_{\tau +1}^m\left(i\right)+b_{\tau +1}^m{\left(i\right)}^{\prime }{\kappa }_{\tau }\left(m\right)\right]}^2{\phi }_{\tau +1}\left(i\right)\\ \text{s}\text{.t}{\kappa }_{\tau }\left(j\mathrm{,}m\right)\ge 0\end{array}$

We solve the unconstrained problem, and the optimal ${\tilde{\kappa }}_{\tau }\left(m\right)={\left({\tilde{\kappa }}_{\tau }\left(\mathrm{1,}m\right)\mathrm{,}\cdots \mathrm{,}{\tilde{\kappa }}_{\tau }\left(n\mathrm{,}m\right)\right)}^{\prime }$ is:

${\tilde{\kappa }}_{\tau }\left(m\right)=-{\left[{\displaystyle \underset{i=m}{\overset{m+n}{\sum }}}{\phi }_{\tau +1}\left(i\right)\cdot b_{\tau +1}^m\left(i\right)b_{\tau +1}^m{\left(i\right)}^{\prime }\right]}^{-1}\cdot \left[{\displaystyle \underset{i=m}{\overset{m+n}{\sum }}}{\phi }_{\tau +1}\left(i\right)\cdot b_{\tau +1}^m\left(i\right)\cdot a_{\tau +1}^m\left(i\right)\right]$

The optimal solution of the constrained problem is ${\kappa }_{\tau }\left(m\right)={\left({\kappa }_{\tau }\left(1,m\right),\cdots ,{\kappa }_{\tau }\left(n,m\right)\right)}^{\prime }$ where

${\kappa }_{\tau }^{*}\left(j,m\right)=\{\begin{array}{ll}{\tilde{\kappa }}_{\tau }\left(j,m\right)\hfill & \text{if}{\tilde{\kappa }}_{\tau }\left(j,m\right)\ge 0\hfill \\ 0\hfill & \text{if}{\tilde{\kappa }}_{\tau }\left(j,m\right)<0\hfill \end{array}$

Hence, the optimal solution of the dual problem is

${\kappa }_t^{\mathrm{<mo>\; *\; </mo>}}\left(m\right)={\left({\kappa }_t^{\mathrm{<mo>\; *\; </mo>}}\left(\mathrm{1,}m\right)\mathrm{,}\cdots \mathrm{,}{\kappa }_t^{\mathrm{<mo>\; *\; </mo>}}\left(n\mathrm{,}m\right)\right)}^{\prime }$

for $t=0,1,2,\cdots ,T-1$ and $m=1,2,\cdots ,nt+1$ , with

${\kappa }_t^{*}\left(j,m\right)=\{\begin{array}{ll}{\tilde{\kappa }}_t\left(j,m\right)\hfill & \text{if}{\tilde{\kappa }}_t\left(j,m\right)\ge 0\hfill \\ 0\hfill & \text{if}{\tilde{\kappa }}_{\tau -1}\left(j,m\right)<0\hfill \end{array}$

where ${\tilde{\kappa }}_t\left(m\right)={\left({\tilde{\kappa }}_t\left(1,m\right),\cdots ,{\tilde{\kappa }}_t\left(n,m\right)\right)}^{\prime }$ is:

${\tilde{\kappa }}_t\left(m\right)=-{\left[{\displaystyle \underset{i=m}{\overset{m+n}{\sum }}}{\phi }_{t+1}\left(i\right)\cdot b_{t+1}^m\left(i\right)b_{t+1}^m{\left(i\right)}^{\prime }\right]}^{-1}\cdot \left[{\displaystyle \underset{i=m}{\overset{m+n}{\sum }}}{\phi }_{t+1}\left(i\right)\cdot b_{t+1}^m\left(i\right)\cdot a_{t+1}^m\left(i\right)\right],$

${\phi }_{t+1}\left(m\right)={\displaystyle \underset{i=m}{\overset{m+n}{\sum }}}{\left[a_{t+2}^m\left(i\right)+b_{t+2}^m{\left(i\right)}^{\prime }{\kappa }_{t+1}^{*}\left(m\right)\right]}^2{\phi }_{t+2}\left(i\right).$

Hence, the risk neutral probability with optimal ${\kappa }^{\mathrm{<mo>\; *\; </mo>}}$ is

$Q\left({\omega }_i\right)={\displaystyle \underset{t=1}{\overset{T}{\prod }}}\frac{{\left(-1\right)}^{e_t^i}\left[\left|D_t^{e_{t-1}^i}\left(e_t^i\right)\right|+{{\displaystyle \sum }}_{j=1}^n\left|{\tilde{D}}_t^{e_{t-1}^i}\left(e_t^i,j\right)\right|S_{t-1}\left(j,e_{t-1}^i\right){\kappa }_{t-1}^{*}\left(j,e_{t-1}^i\right)\right]}{{{\displaystyle \sum }}_{j=1}^{n+1}{\left(-1\right)}^j\left|D_t^{e_{t-1}^i}\left(j\right)\right|},$

and the optimal terminal wealth is

$\begin{array}{c}{V}_T^{{\kappa }^{*}}({\omega }_i)=\beta +\left[\frac{v-\beta E\left[L^{{\kappa }^{*}}/B_T^{{\kappa }^{*}}\right]}{E\left[{\left(L^{{\kappa }^{*}}\right)}^2/{\left(B_T^{{\kappa }^{*}}\right)}^2\right]}\right]L^{{\kappa }^{*}}/B_T^{{\kappa }^{*}}=\beta +\left[\frac{v{B}_T^{{\kappa }^{*}}-\beta }{E\left[{\left(L^{{\kappa }^{*}}\right)}^2\right]}\right]L^{{\kappa }^{*}}\\ =\beta +\frac{1}{{\left(n+1\right)}^T}\left[\frac{v{B}_T^{{\kappa }^{*}}-\beta }{E\left[Q{\left({\omega }_i\right)}^2\right]}\right]Q\left({\omega }_i\right).\end{array}$

Hence, the expectation and variance of terminal wealth are:

$E\left(V_T\right)=a\beta +bv,$

$Var\left(V_T\right)=c{\left(v{B}_T^{{\kappa }^{*}}+\beta \right)}^2,$

where

$a=1\frac{1}{{\left(n+1\right)}^T}\frac{E\left[Q\left(\omega \right)\right]}{E\left[Q{\left(\omega \right)}^2\right]},$

$b=\frac{1}{{\left(n+1\right)}^T}\frac{E\left[Q\left(\omega \right)\right]}{E\left[Q{\left(\omega \right)}^2\right]}{B}_T^{{\kappa }^{*}},$

$c=\frac{1}{{\left(n+1\right)}^{2T}}\frac{E\left[Q{\left(\omega \right)}^2\right]-E\left[Q\left(\omega \right)\right]}{{\left(E\left[Q{\left(\omega \right)}^2\right]\right)}^2}.$

The optimal $\beta$ must satisfy the optimality condition of $\frac{\text{d}U}{\text{d}\beta }=0$ , that is,

${\beta }^{*}=\frac{a+2\omega cv{B}_T^{{\kappa }^{*}}}{2\omega c}.$

6. Optimal Trading Strategy

Let $\alpha =\frac{1}{{\left(n+1\right)}^T}\left[\frac{v{B}_T^{{\kappa }^{*}}-\beta }{E\left[Q{\left({\omega }_i\right)}^2\right]}\right]$ , so $V_T\left({\omega }_i\right)=\beta +\alpha Q\left({\omega }_i\right)$ .

Proposition 6.1. For any $t\in \left\{\mathrm{0,1,}\cdots \mathrm{,}T\right\}$ , $V_t\left(\omega \right)$ are equivalent for

$\omega \in {\tilde{\Omega }}_{l_t}=\left\{\left(e_1,\cdots ,e_T\right);\left(e_1,\cdots ,e_t\right)={\tilde{\omega }}_{l_t}\right\},$

where ${\tilde{\omega }}_{l_t}$ is belong to the $t$ period sample space, and $l_t\in \left\{\mathrm{1,2,}\cdots \mathrm{,}{\left(n+1\right)}^t\right\}$ . We denote

$V_t\left(\omega \right)=V_t\left({\tilde{\omega }}_{l_t}\right)\mathrm{.}$

We have the relationship between $V_t$ and $V_{t+1}$ for any $t$ :

$V_t\left(\omega \right)\cdot \left[1+r_{t+1}+{{\pi }^{\prime }}_{t+1}\left(R_{t+1}+B_{t+1}{\kappa }_t-r_{t+1}1\right)\right]=V_{t+1}\left(\omega \right)\mathrm{.}$

So we can iteratively derive $V_t$ and corresponding trading strategy ${\pi }_{t+1}$ for each $t$ .

For $t=T-1$ , we consider $\omega \in {\Omega }_{l_{T-1}}=\left\{\left(e_1,\cdots ,e_T\right);\left(e_1,\cdots ,e_{T-1}\right)={\tilde{\omega }}_{l_{T-1}}\right\}$ $\left(l_{T-1}\in \left\{\mathrm{1,2,}\cdots \mathrm{,}{\left(n+1\right)}^{T-1}\right\}\right)$ , and $\Omega ={\Omega }_1\cup \cdots \cup {\Omega }_{{\left(n+1\right)}^{T-1}}$ . For each i there are $n+1$ element in the set ${\Omega }_i$ . For an arbitrary set ${\Omega }_{l_{T-1}}$ , we notate the $n+1$ element in it as ${\omega }_1^{l_{T-1}}\mathrm{,}\cdots \mathrm{,}{\omega }_{n+1}^{l_{T-1}}$ . So

$\begin{array}{l}{V}_{T-1}\left({\tilde{\omega }}_{l_{T-1}}\right)\cdot \left[1+r_T+{{\pi }^{\prime }}_T\left(R_T\left({\omega }_1^{l_{T-1}}\right)+B_T{\kappa }_{T-1}-r_{T}1\right)\right]=V_T\left({\omega }_1^{l_{T-1}}\right)\\ V_{T-1}\left({\tilde{\omega }}_{l_{T-1}}\right)\cdot \left[1+r_T+{{\pi }^{\prime }}_T\left(R_T\left({\omega }_2^{l_{T-1}}\right)+B_T{\kappa }_{T-1}-r_{T}1\right)\right]=V_T\left({\omega }_2^{l_{T-1}}\right)\\ ⋮\\ V_{T-1}\left({\tilde{\omega }}_{l_{T-1}}\right)\cdot \left[1+r_T+{{\pi }^{\prime }}_T\left(R_T\left({\omega }_{n+1}^{l_{T-1}}\right)+B_T{\kappa }_{T-1}-r_{T}1\right)\right]=V_T\left({\omega }_{n+1}^{l_{T-1}}\right)\end{array}$

Rewrite the above equations as the matrix form as $G\cdot X=b$ , where

$G=\left(\begin{array}{cc}{V}_T\left({\omega }_1^{l_{T-1}}\right)& {\left(R_T\left({\omega }_1^{l_{T-1}}\right)+B_T{\kappa }_{T-1}-r_{T}1\right)}^{\prime }\\ ⋮& ⋮\\ V_T\left({\omega }_{n+1}^{l_{T-1}}\right)& {\left(R_T\left({\omega }_{n+1}^{l_{T-1}}\right)+B_T{\kappa }_{T-1}-r_{T}1\right)}^{\prime }\end{array}\right)$

$X=\left(\begin{array}{c}1/V_{T-1}\left({\tilde{\omega }}_{l_{T-1}}\right)\\ {\pi }_T\end{array}\right)$

$b=\left(1+r_T\right)1$

If $G$ is full rank, $X=G^{-1}b$ .

Generally, for $t=\tau$ , we consider $\omega \in {\tilde{\Omega }}_{l_{\tau }}^{\tau }=\left\{\left(e_1,\cdots ,e_{\tau +1}\right);\left(e_1,\cdots ,e_{\tau }\right)={\tilde{\omega }}_{l_{\tau }}\right\}$ $\left(l_{\tau }\in \left\{\mathrm{1,2,}\cdots \mathrm{,}{\left(n+1\right)}^{\tau }\right\}\right)$ , and ${\tilde{\Omega }}^{\tau +1}={\tilde{\Omega }}_1^{\tau }\cup \cdots \cup {\tilde{\Omega }}_{{\left(n+1\right)}^{\tau }}^{\tau }$ . For each i there are $n+1$ element in the set ${\tilde{\Omega }}_i^{\tau }$ . For an arbitrary set ${\tilde{\Omega }}_{l_{\tau }}^{\tau }$ , we notate the $n+1$ element in it as ${\omega }_1^{l_{\tau }}\mathrm{,}\cdots \mathrm{,}{\omega }_{n+1}^{l_{\tau }}$ . So

$\begin{array}{l}{V}_{\tau }\left({\tilde{\omega }}_{l_{\tau }}\right)\cdot \left[1+r_{\tau +1}+{{\pi }^{\prime }}_{\tau +1}\left(R_{\tau +1}\left({\omega }_1^{l_{\tau +1}}\right)+B_{\tau +1}{\kappa }_{\tau }-r_{\tau +1}1\right)\right]=V_{\tau +1}\left({\omega }_1^{l_{\tau +1}}\right)\\ V_{\tau }\left({\tilde{\omega }}_{l_{\tau }}\right)\cdot \left[1+r_{\tau +1}+{{\pi }^{\prime }}_{\tau +1}\left(R_{\tau +1}\left({\omega }_2^{l_{\tau +1}}\right)+B_{\tau +1}{\kappa }_{\tau }-r_{\tau +1}1\right)\right]=V_{\tau +1}\left({\omega }_2^{l_{\tau +1}}\right)\\ ⋮\\ V_{\tau }\left({\tilde{\omega }}_{l_{\tau }}\right)\cdot \left[1+r_{\tau +1}+{{\pi }^{\prime }}_{\tau +1}\left(R_{\tau +1}\left({\omega }_{n+1}^{l_{\tau +1}}\right)+B_{\tau +1}{\kappa }_{\tau }-r_{\tau +1}1\right)\right]=V_{\tau +1}\left({\omega }_{n+1}^{l_{\tau +1}}\right)\end{array}$

Rewrite the above equations as the matrix form as $G_{\tau }\cdot X_{\tau }=b_{\tau }$ , where

$G_{\tau }=\left(\begin{array}{cc}{V}_{\tau +1}\left({\omega }_1^{l_{\tau }}\right)& {\left(R_{\tau +1}\left({\omega }_1^{l_{\tau }}\right)+B_{\tau +1}{\kappa }_{\tau }-r_{\tau +1}1\right)}^{\prime }\\ ⋮& ⋮\\ V_{\tau +1}\left({\omega }_{n+1}^{l_{\tau }}\right)& {\left(R_{\tau +1}\left({\omega }_{n+1}^{l_{\tau }}\right)+B_{\tau +1}{\kappa }_{\tau }-r_{\tau +1}1\right)}^{\prime }\end{array}\right)$

$X_{\tau }=\left(\begin{array}{c}1/V_{\tau }\left({\tilde{\omega }}_{l_{\tau }}\right)\\ {\pi }_{\tau +1}\end{array}\right)$

$b_{\tau }=\left(1+r_{\tau +1}\right)1$

If $G_{\tau }$ is full rank, $X_{\tau }=G_{\tau }^{-1}{b}_{\tau }$ .

7. Numerical Example

We consider a market with one risky security and one bond, and the investment horizon is $T=3$ . Suppose the bond price is constant. The prices of the risky security are:

The risk neutral probability in market $M_{\kappa }$ are:

We solve the dual problem:

$\begin{array}{l}max{{\displaystyle \sum }}_{i=1}^8{Q}_{\kappa }{\left({\omega }_i\right)}^2\\ \text{s}\text{.t}{\kappa }_t\ge \mathrm{0\; <mi>\; </mi>\; <mi>\; </mi>}\text{for}t=\mathrm{1,2,3\; <mi>\; </mi>\; <mi>\; </mi>}\end{array}$

The optimal solution of this is easily found to be:

${\kappa }_2\left(1\right)={\kappa }_2\left(2\right)={\kappa }_2\left(3\right)=0$

${\kappa }_1\left(1\right)=\frac{5}{68},\mathrm{<mi>\; </mi>\; <mi>\; </mi>}{\kappa }_1\left(2\right)=0$

${\kappa }_0\left(1\right)=0$

The optimal value is

Finally, we get the optimal trading strategy of the original problem by solving some linear equations. The optimal strategy are

8. Conclusion

Optimal mean-variance multiperiod portfolio selection with no shorting con- straints problem is studied in the paper. We connect the original mean-variance problem to an auxiliary problem by using an embedding technique. Since the auxiliary problem is difficult to solve directly, we extend the literature by using duality theory and martingale approach to do the analysis. Finally, the derived analytical optimal multiperiod portfolio strategy provides investors with the best strategy to follow in a no-short selling dynamic investment environment. The limitation in this paper is that we derive the optimal portfolio policy by maxi- mizing the quadratic utility function. A future research subject is investigation of an optimal solution using different utility objective function.

Acknowledgements

Jinan University scientific research cultivation and Innovation Fund, Number: 17JNQN025.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Markowiz, H. (1983) Portfolio Selection. The Journal of Finance, 7, 77-91.
[2]	Merton, R.C. (1972) An Analytic Derivation of the Efficient Portfolio. The Journal of Financial and Quantitative Analysis, 7, 13-15. https://doi.org/10.2307/2329621
[3]	Duan, L. and Ng, W.L. (2000) Optimal Dynamic Portfolio Selection: Multiperiod Mean-Variance Formulation. Mathematical Finance, 10, 387-406. https://doi.org/10.1111/1467-9965.00100
[4]	Li, X., Zhou, X.Y. and Lim, A.E.B. (2002) Dynamic Mean-Variance Portfolio Selection with No-Shorting Constraints. Journal on Control and Optimization, 40, 1540-1555. https://doi.org/10.1137/S0363012900378504
[5]	Xu, G.L. and Shreve, S.E. (1992) A Duality Method for Optimal Consumption and Investment under Short-Selling Prohibition. i. General Market Coefficients. Annals of Applied Probability, 2, 87-112. https://doi.org/10.1214/aoap/1177005772
[6]	Xu, G.L. and Shreve, S.E. (1992) A Duality Method for Optimal Consumption and Investment under Short-Selling Prohibition. ii. Constant Market Coefficients. Annals of Applied Probability, 2, 314-328. https://doi.org/10.1214/aoap/1177005706
[7]	Pliska, S.R. (1986) A Stochastic Calculus Model of Continuous Trading: Optimal Portfolios. Mathematics of Operations Research, 11, 371-382. https://doi.org/10.1287/moor.11.2.371