Received 25 April 2016; accepted 23 May 2016; published 26 May 2016
1. Introduction
It was suggested that coherent X-ray emission could be produced in the collision of highly energetic electrons with multiply charged ions [1] . The first soft X-ray laser amplification was demonstrated in neon-like sellenium [2] in which a high energy neodymium glass laser is used to strike a thin foil of selenium where it was evaporize and create plasma of neon-like selenium. The high energy electrons in the plasma collide and excite the neon-like selenium ions in the plasma and emit a coherent soft X-ray transition with wavelength 21 nm [3] . Shortly afterwords a lot of experimentally work was done to check the possibility of the emission of laser radiation from different ions. The authors have done a lot of work to calculate the atomic properties and predict the possible laser transitions from different ions [4] - [6] . Recently a laser transitions from Ne-like Ti, V, Cr, Fe and Co were observed [7] .
In this paper, we apply the electron excitation model to predict new gain lines from neon like gallium and germanium, comparing the results with the experimental work.
2. Calculation of Level Population
The gain coefficient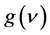 
of a medium is related to the intensity of the radiation as follow
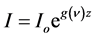(1)
where 
is the initial incident intensity of the radiation and I is the intensity after length z. In high density plasma, Doppler broadening is the dominant type of broadening [8] - [10] and the gain coefficient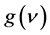 
can be given by [11]
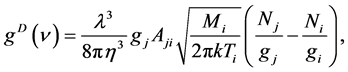(2)
where we have used 
and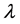 
is the transition wavelength, 
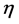is the refractive index 
where
, 
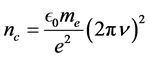and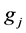 
are the statistical weights of the lower and upper levels respectively,
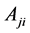is the transition rate, 
is the ion mass, 
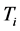is the ion temperature and ![]()
and ![]()
are the lower and upper level populations.
Taking the electron impact excitation and deexcitation as the main mechanism for the population of states we could define our rate equation to be
![]()
(3)
where ![]()
and ![]()
are the excitation and deexcitation rates respectively. Solving Equation (3) for the quasi steady states![]()
, and finding the fractional population![]()
.
In order to determine the population of states we need to determine the total number of atoms ![]()
and to do that we use the same properties of the first experiment of the neon like Selenium. In that experiment a collimated beam of high power laser was cocenterated on a cylinderical target with length 1.2 cm and 200 mm in diameters [12] [13] using the ratio of the ion temperature ![]()
to the electron temperature ![]()
to be 0.4 as in [14] and in a good agreement with [8] . Five electron temperatures were taken for each ion.
The total number of atoms ![]()
could be determined as
![]()
(4)
where ![]()
is the target density, V is the volume, A is the atomic weight of the atoms, ![]()
is the population of ions in the ionization stage I and f is the ion fraction. The fraction of the neon like atoms that was produced in the plasma was taken to be![]()
. Our intiuation behind that ratio was the He-Ne laser, the laser emission from Helium-Neon laser was due to the Neon atoms while their population was very low comparing with the Helium gas as![]()
.
All our calculations were done by our code written in python programming language where we put Equation (3) in the matrix form and apply the boundary condition Equation (4) to solve the equations for![]()
. We used the flexible atomic code (FAC) [15] which is fully relativistic in calculating the energy levels and the effective collision strength using the distorted wave approximation.
Practically the cross section averaged over the velocity distribution of the scattered electrons is very important and is called the rate coefficient and has the form
![]()
(5)
as a function of energy. The cross section and the velocity of the scattered electrons could be expressed as
![]()
(6)
and the Maxwellian distribution function is given by
![]()
(7)
Substituting in Equation (5) we get
![]()
(8)
where the integral usually defined as the effective collision strength ![]()
is
![]()
(9)
where it is the Maxwellian average of the collision strength. Equation (8) becomes
![]()
(10)
where ![]()
is the collisional de-excitation rate expressed as a function of the effective collision strength![]()
, the statistical weight ![]()
of the upper state and the electron temperature![]()
. By the same way the excitation rate coefficient ![]()
could be expressed as [16]
![]()
(11)
where ![]()
is the energy difference between the initial and final states of the transitions. In the derivation we have used (![]()
) and subsequently (![]()
). Both excitation and de-excitation rates could be expressed as
![]()
(12)
Gain coefficient ![]()
is related to the cross section ![]()
as follow
![]()
(13)
where ![]()
is the population inversion factor and can be expressed as
![]()
(14)
where ![]()
and ![]()
are the stimulated and the absorption cross sections, ![]()
and ![]()
are the population densities of states ![]()
and ![]()
respectively and ![]()
and ![]()
are the statistical weights of states ![]()
and ![]()
respectively.
During the laser pumping, the population inversion should occurs and then the population of the higher energy levels becomes greater than the lower ones ![]()
and subsequently the inversion factor decrease and becomes less than unity as shown from Equation (14).
3. Results and Discussion
The atomic data of the gallium and germanium ions were relativistically calculated using FAC v1.1.3 [15] and the effective collision strengths were determined using the distorted wave approximations. Five electron temperatures (![]()
and 1500 eV) were taken for each ion and the gain coefficients were calculated. A wide range of the electron densities were taken (![]()
to![]()
).
The resulted curves have the same behavior for the different electron temperatures, so the population inversion![]()
, effective collision strength ![]()
and gain ![]()
at electron temperature ![]()
for both ions are shown in Figure 1 and Figure 2.
Gain coefficients ![]()
for both ions ![]()
and ![]()
are listed in Table 1 and Table 2 at five different electron plasma temperatures (![]()
and 1500 eV).
In neon like Gallium ions![]()
, the following line transitions [17] - [19] ((10-2), (9-2) and (13-4)) as in Table 1 were detected with gains (4.3, 3.1 and 2.8 cm−1) respectively which agrees with our gains values except the transition (10-2) have higher gain value than our calculations. Also this line (8-2) was detected.
In neon like Germanium ions![]()
, the following line transitions [19] - [23] ((9-2), (13-4), (34-30), (8-2) and (6-2)) as seen in Table 2 and the gain for (34-30) was detected to be 30 cm−1 which is greater than our calculations and other gains has a good agreement with our calculations.
4. Conclusion
All possible transitions with gain coefficients ![]()
are calculated for both neon-like gallium and germanium. Some of these lines were experimentally observed moreover shorter laser transitions are predicted from our calculations of the neon-like gallium and germanium ions. The collisional excitation model is sufficient to produce a population inversion and enough for explaining the emitted soft X-ray lasers.