Stability Analysis of Multi-Dimensional Linear Discrete System and Root Distribution Using Sign Criterion with Real Coefficients ()
Received 4 March 2016; accepted 21 March 2016; published 25 March 2016
1. Introduction
In the last year, a big amount of research was dedicated to develop technique for the multidimensional system to work the solutions of several physical problems and special emphasis has been placed on the output feedback stabilization problem and the multidimensional stability problem. The multidimensional linear system plays an important role in control theory and circuit and system theory and arises in many fields such as digital filters, image processing, video processing, seismic data processing, bio-medical digital processing, control processing of radar and sonar data, medical imagery, etc. The design of recursive digital filters is relatively simple, but the stability constraints, associated with the design of such filters, are a major problem. Stability analysis of multidimensional system is much more complex than that of one dimensional system. To reduce complexity in this paper the multi-dimensional characteristics equation has been converted into equivalent one-dimensional characteristics equation and the coefficients of equivalent one-dimensional characteristics polynomial have been utilized for stability test using proposed single modified Jury tabulation and sign criterion.
2. Literature Survey
Stability means stable operation of a multi-dimensional system even when some changes in the parameter of a system. Hence, Stability is an essential property and plays an important role in the multi-dimensional linear system. Therefore, stability is studied and described by many analysts. The test procedure introduced by Jury explains the stability using routh table. Later, it is then modified by Blanchard and Jury himself in 1961 which is similar to routh table and very simple for hand computation for any order linear discrete systems was demonstrated in [1] . De la Sen revealed that the asymptotic stability [2] of a class of linear time invariant system. Tests demonstrated in [3] derived an s-domain scattering Hurwitz polynomials. These tests were based on inner matrices which reduce the complexity of test procedure. Serban et al. proposed [4] a new multi-dimensional necessary and sufficient bounded input and bounded output (BIBO) stability based on slice type extensions of the schur coefficients, which only needed unique conditions to be checked. An efficient stability test and less computation is comparison with modified Jury test was posed in [5] . Multi-dimensional linear shift invariant digital filter are reviewed and extended in [6] by Benidir. Also the geometrical properties of stability domain of recursive filters were studied. Jury coordination with Bose in [7] developed a systematic procedure for three dimensional filters which is based on repeated applications of extended hermit or Schur-Cohn formulation. Also in digital filters [8] proposed a generations of a number of multi variable polynomial by using finite number of multi variable matrix multiplications followed by reduction of these polynomial. Bose et al. [9] presented a constructive algorithm, this method was very efficient for calculation of determinants of large matrices with multi variable polynomial entries and the results obtained in [10] gave the procedure for ascertaining robust stability of discrete systems which required only use of bilinear transformation and simple arithmetic operations. Hertz et al. [11] proved that the sufficient conditions were simple enough to apply for the stability tests. Using fast Fourier transform, in [12] presented an efficient algorithm which computes the determinant of polynomial matrix. The implementation procedure in [13] for stability test for single dimensional digital filter was extended to multi-dimensional case which is verified using computer program. The criterion in [14] was based on slice functions mechanisms and recent n dimensional extensions of single dimensional Schur coefficient associated to a polynomial. Novel stability criterion for multi-dimensional digital and analog filters with rational transfer functions is given in [15] . Dameravenkata et al. in [16] had presented stability test based on the uniqueness theorem for multi-dimensional minimum phase polynomials presented and needed to use higher order fast Fourier transform to stabilize the class of m-D polynomials not having zeros on the unity hyper circle. Jury in [17] made an approach to convert two dimensional difference equations to a single dimensional difference equation. Bose Addresses the development of more efficient local positivity testing [18] method for multi-dimensional systems. A stability theorem for n-dimensional recursive filters was proved by justice et al. in [19] where the denominator of the filter is an n-dimensional power series. This generalized procedure has been used to solve several versions of the problem not solvable by the standard one-ended imbedding technique. Anderson et al. in [20] proposed a new procedure for testing asymptotic stability, which did not involve the use of bilinear transformations. In the theory of two-dimensional digital filtering it is often interest to know whether prescribed polynomial satisfies the required necessary and sufficient conditions refereed in [21] . Rao et al. in [22] revealed a new, simple and unified way to eliminating both types of singularities encountered in the development of Jury table. Nagrath et al. in [23] proposed an algebraic criterion for determining whether or not the roots of the characteristics polynomial within a unit circle there by determining the system stability using Jury stability method. Hu et al. proposed a polynomial array method and applications in stability tests for one and two dimensional discrete systems were discussed in [24] . Ezra Zehab et al. revealed a new theorems in [25] which can be used to find the zeros set of a variable where the distinguished boundary of the parameters domain of definition, in the closed plane. The results are used to derive a new simplified procedure for an m-dimensional stability tests.
3. Proposed Method
In the more general case of here m-dimensional [19] linear discrete system with a rational transfer function
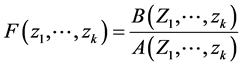(1)
The corresponding stability criterion is;
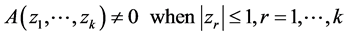(2)
The direct implementation of (2) engenders extraordinary computation and storage requirements, and the following conditions were proven to be equivalent to (2)
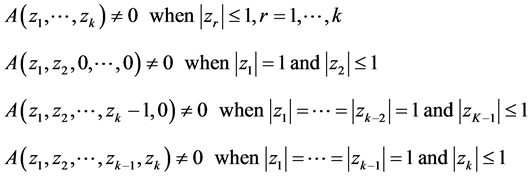(3)
Let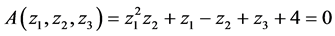 
Necessary condition:
1) With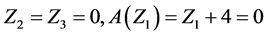 
By Using reciprocal of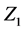 
and with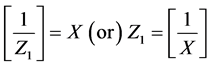 
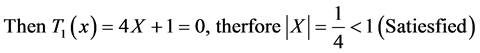
2) With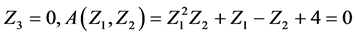 
By using reciprocal of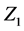 
and 
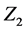with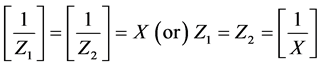 
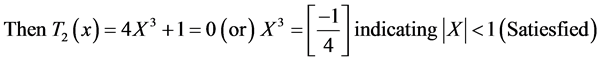
The Equation (3) have been highly useful as criteria for the stability of multi-dimensional [21] filters. In above example method used for to check the necessary conditions consumes more arithmetic operations which can be replaced by proposed simple necessary and sufficient conditions in this paper.
Consider the following general multi-dimensional [24] characteristics equation.
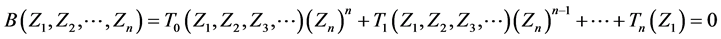(4)
The variables Z in equation (4) can be formulated as equation (5) by taking the inverse of variable-Z [20] to find the equivalent one dimensional characteristics equations from the given multi-dimensional characteristics polynomial.
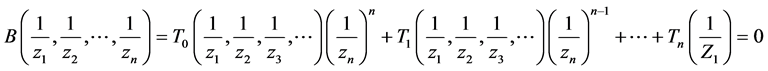(5)
After simplification the above equation becomes
![]()
(6)
Thus the ![]()
can be used to check the aperiodic stability of the give multi-dimensional system.
3.1. Stability Criterion of Real Polynomial
The nth degree characteristic of a LTIDS can be represented as
![]()
, where ![]()
is real coefficient and![]()
.
The condition for stability of LTIDS is that, all the roots system characteristics equation ![]()
should lie within the unit circle or in other words![]()
. To infer this situation the necessary conditions for the roots of ![]()
to lie inside the unit circle are written from (Jury, 1964).
1) ![]()
2) ![]()
3) ![]()
Modified-Jury Table and Proposed Sufficient Conditions
The proposed sufficient conditions the roots of ![]()
to lie inside the unit circle are obtained from the following table (Table 1).
Simple modification is needed in the Jury’s table [23] formation in order to obtain the sign based sufficient condition. The proposed table formation is done with the following rules:
First row always consists of coefficient of the polynomial considered.
1) The elements of row ![]()
consist of the elements of the row ![]()
in reverse order, where
![]()
; n = Order of the polynomial.
2) The elements of the ![]()
row are obtained by taking determinants of ![]()
matrices
Constitute of first and ![]()
columns of (![]()
) and ![]()
row, where ![]()
![]()
The process of calculating the each row elements ![]()
is extended till the single elements row ![]()
The n-sufficient conditions are formed from the table by examining the algebraic signs of the last elements in odd Rows ![]()
and ![]()
called “![]()
series” where ![]()
(Jury, 1964).
![]()
.
Sufficient conditions for stability: Negative ![]()
values (1).
Any positive ![]()
indicates the instability of the system. In order to find the root distribution of such unstable
systems. The same series considered to be exposed to the proposed sign criterion which is explication in the subsequent session.
3.2. Proposed Criterions for Root Locations
To determine the number of roots a new common sign strategy is proposed which concerns the sign series of![]()
. The Sign criterion is always applied only from the proposed table formation methodology is applied.
3.2.1. Proposed Sign Criterion for Outside Unit Circle Roots
Proposed sign criterion to obtain the number of OUC roots is “Number of odd numbered positive signs added with the Following negative signs in the ![]()
sign series”.
3.2.2. Proposed Sign Criterion for Inside Unit Circle Roots
The above mentioned sign criterion can be used to find IUC roots but after two sign change in ![]()
series. Change the sign of first elements of ![]()
series & the ![]()
elements which is immediately following the “all zero row” (If exits). Thus it forms a new ![]()
sign series. Proposed sign criterion to obtain the number of IUC roots is “number of odd numbered positive signs added with their following negative signs in the ![]()
sign series after specific sign change”.
4. Root Distribution of Real Polynomial
Various cases of discrete system are taken into account to experiment the proposed sign criterion. It is always desirable to determine the root distribution in more direct manner. Hence nevertheless the reliability of the proposed Criterion of OUC and IUC roots in all the cases, in this paper only one sign criterion (either OUC or IUC) is attempted to Explore to entire root distributions expect the case “All zero row-Asymmetric coefficients polynomial” which is discussed in section.
The special cases are:
1) Non singular,
2) Singular,
a) Single element zero,
b) “All zero row”,
1) Immediate “all zero row” (or) symmetric coefficient polynomial,
2) Mediate “all zero row”.
4.1. Non-Singular Case
Non-singular (regular) case doesn’t encounter any zero elements during table formation and hence the system is not having any zero on the unit circle.
Step1: Find the OUC roots using the criterion stated in the section.
Step2: IUC roots = n-OUC roots.
4.2. Singular Case
A singular case generally is encountering zero elements (either single zero or all elements zero of a row) during the development of the table
4.2.1. Single Zero Element in a Row
A single zero anywhere in an array will not affect the continuance of table formation in the proposed criterion. Any “Zero![]()
” should be neglected during the sign count (Rao, 1976) and also for the sign change. Hence the procedure to Find root distribution of single zero element case is similar to that of non-singular case. If the last row (single element Row) ![]()
is zero then it is consider as “all zero row” case which is elaborated below.
4.2.2. All Zero Row
If the tabulation encounters any “all zero row” then there is a possibility of roots lying on the unit circle. Hence the
Three types of root distributions OUC, IUC and on the circle are determined. An “all zero row” occurs anywhere in the table should be replaced by the derivative coefficients of the previous odd row![]()
.
Hence new![]()
, taking conjugate/inverse is not needed as in the case of Jury 1964.
4.2.3. Immediate All Zero Row (or) Symmetric Coefficient Polynomial
In the case of real polynomials, if the coefficients are symmetric then the all zero will appear immediately in the third row itself during the table construction. The polynomial coefficients exhibit symmetry with respect to their midpoint i.e.)![]()
, where ![]()
the all zero is replaced by the derivative coefficients of previous odd row. Even through the proposed IUC & OUC sign criterions are compatible, determined of OUC roots alone is enough to discover the entire root distributions of the polynomial. It is grounded on the important observation stated below. Observation: in case of symmetric coefficients polynomials (or) immediate “all zero row” case, the number of roots lying outside the unit circle is always equivalent to the number of roots lying inside the unit circle.
Step 1: Find the OUC roots using the criterion stated in the section of sign criterion for OUC roots.
Step 2: IUC roots = OUC roots.
Step 3: Number of roots lying on the unit circle = n − 2 (OUC roots).
4.2.4. Mediate Zero Row
It is essential to find OUC and IUC roots separately using the proposed criterion.
Step 1: Find the OUC roots using the criterion stated in the section of sign criterion for OUC roots
Step 2: Find the IUC roots using the criterion stated in the section of sign criterion for IUC roots.
Step 3: Number of roots lying on the unit circle = n − (OUC roots + IUC roots).
5. Illustrations
Example 1: Stable [25]
Let ![]()
To convert multi-dimensional characteristics polynomial equation into equivalent one-dimensional characteristics polynomial equation
![]()
![]()
![]()
![]()
![]()
Necessary conditions:
1) ![]()
2) ![]()
3) ![]()
Sufficient conditions:
From the above illustration, all ![]()
values are negative and the sufficient conditions are satisfied. Thus it can be concluded that ![]()
has three roots with![]()
. Hence the system is stable.
Example 2: One zero element [25]
Let ![]()
To convert multi-dimensional characteristics polynomial equation into equivalent one-dimensional characteristics polynomial equation
![]()
Necessary conditions:
1) ![]()
2) ![]()
3) ![]()
Sufficient conditions:
Neglecting the zero in the ![]()
series, the OUC root is one. The remaining one root is inside the unit circle.
Example 3: Unstable [24]
Let ![]()
To convert multi-dimensional characteristics polynomial equation into equivalent one-dimensional characteristics polynomial equation
![]()
Necessary conditions:
1) ![]()
2) ![]()
3) ![]()
Sufficient conditions:
A zero in the array did not affect the continuance of the table formation. From the above illustration, it is found that the sufficient conditions are not satisfied and the system is unstable, hence there is at least one root outside the unit circle. From sign criterion OUC roots are two and hence IUC roots are two.
Example 4: Mediate all zero row [25]
Let ![]()
To convert Multi-dimensional characteristics polynomial equation into equivalent one-dimensional characteristics polynomial equation
![]()
Necessary conditions:
1) ![]()
2) ![]()
3) ![]()
Sufficient conditions:
From the illustrations, no roots are lying outside the unit circle, roots inside the unit circle are two and no roots lying on the unit circle.
Example 5: Mediate All Zero row [11]
![]()
To convert multi-dimensional characteristics polynomial equation into equivalent one-dimensional characteristics polynomial equation
![]()
Necessary conditions:
1) ![]()
2) ![]()
3) ![]()
Sufficient conditions:
In the above illustrations, because of the all zero row there may be the existence of roots lying on the unit circle. Therefore all the root distributions are examined. From the proposed sign criterion, OUC root is one, IUC roots are two and hence roots lying on the unit circle are two.
Example 6: Immediate all zero row [22]
![]()
To convert multi-dimensional characteristics polynomial equation into equivalent one-dimensional characteristics polynomial equation
![]()
Necessary conditions:
1. ![]()
2. ![]()
3. ![]()
Sufficient conditions:
In the above problem, the polynomial has symmetric co-efficient and hence the “all zero array’ arises immediately in the third row. For symmetric co-efficient polynomial, IUC roots and OUC roots count are the same. Therefore number of roots lying outside the unit circle is two, inside the unit circle is two, on the unit circle is zero.
6. Conclusion
From the preceding illustrative examples it is easily absorbed that the proposed schemes for stability investigation are direct and straight forward. The procedure to find the root distribution of the unstable system emulates the Jury table formation. The criterion which is based on the sign of specific elements of the tabulation gives the number of roots lying inside, outside and on the unit circle. The conception is exemplified for stable, unstable and singular problems in real cases that are dealt in the erstwhile works. Besides the integer growth in higher order system, calculation of this method is easier, division free and direct when compared to the existing methods of finding the root distribution, most of which are discussed in the literature review section.