Applying Linear Controls to Chaotic Continuous Dynamical Systems ()
Received 18 January 2016; accepted 13 March 2016; published 16 March 2016

1. Introduction
We begin with an autonomous continuous dynamical system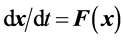 , where
, where 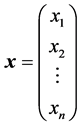 and
and .
.
We use the notation that 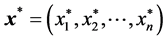 is a rest point, or equilibrium point of
is a rest point, or equilibrium point of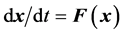 , if
, if .
.
Under some parameter values or initial conditions, the system 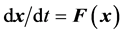 exhibits chaos or hyperchaos. Refer to Yu et al., [2] , for a discussion regarding the differences between chaos and hyperchaos.
exhibits chaos or hyperchaos. Refer to Yu et al., [2] , for a discussion regarding the differences between chaos and hyperchaos.
Control theory attempts to find a controller to apply to the dynamical system that stabilizes the system and eliminates the chaos or hyperchaos. In the context of the autonomous dynamical system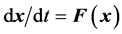 , the investigator searches for a function
, the investigator searches for a function 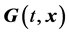 so that
so that 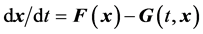 does not exhibit chaos or hyperchaos for the given parameter values and initial conditions that the original system,
does not exhibit chaos or hyperchaos for the given parameter values and initial conditions that the original system, 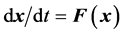 exhibits using those parameter values and initial conditions.
exhibits using those parameter values and initial conditions.
The focus of this paper is to illustrate an automated technique to find a linear control (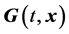 ) of a continuous dynamical system that exhibits chaos or hyperchaos. In subsequent studies, we will focus both on the controller design, conditions when a chaotic system is stabilized, and the physical interpretation of the controller for specific dynamical systems.
) of a continuous dynamical system that exhibits chaos or hyperchaos. In subsequent studies, we will focus both on the controller design, conditions when a chaotic system is stabilized, and the physical interpretation of the controller for specific dynamical systems.
2. Background
Li and Li, [3] , provide examples of several approaches to controlling the chaotic three dimensional Chen-Lee system in their paper and illustrate how different multiple control techniques stabilize the system in their case study. To briefly summarize their results, Li and Li, [3] , provide several approaches to control and provide synchronization of the chaotic Chen-Lee System,
 (1)
(1)
at the origin,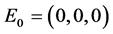 . In their case study they use three feedback controls that are summarized as follows.
. In their case study they use three feedback controls that are summarized as follows.
(1) Linear Feedback Control. Linear ,
, ![]() and
and ![]() terms are included in the x, y, and z equations of system (1). The ki's are feedback coefficients.
terms are included in the x, y, and z equations of system (1). The ki's are feedback coefficients.
(2) Speed Feedback Control. A single control of the form
![]()
is incorporated into the x-equation of system (1). ![]() and
and ![]() are the speed feedback coefficients (see [4] ).
are the speed feedback coefficients (see [4] ).
(3) Doubly-Periodic Function Feedback Control. The control in the X-equation is ![]() and in the Z-equation is
and in the Z-equation is![]() . The functions
. The functions ![]() and
and ![]() are the doubly-periodic functions where
are the doubly-periodic functions where ![]() and
and ![]() are speed feedback coefficients and
are speed feedback coefficients and ![]() is the modulus of the Jacobi elliptic function. Refer to Li and Li, [3] , for details.
is the modulus of the Jacobi elliptic function. Refer to Li and Li, [3] , for details.
The form of the design used to attempt to control a given system can be motivated by many factors. In general, controlling nonlinear high-dimensional chaotic dynamical systems can be a formidable problem, Musielak and Musielak, [1] . Viera and Lichtenberg, [5] , illustrate several examples of controlling chaos using a nonlinear feedback with delay. On the other hand, Tan et al., [4] , develop a controller using a backstopping design.
In this paper, we demonstrate a sequence of algorithms that may be used to find a linear control for a high- dimensional non-linear dynamical system that exhibits chaos or hyperchaos under certain conditions. We show
that a basic linear control of the form![]() , where
, where![]() , can often be used to stabilize high-dimen-
, can often be used to stabilize high-dimen-
sional non-linear chaotic dynamical systems provided that the underlying parameter values are known a priori.
We use a computer algebra system like Mathematica or Maple to implement the procedure to find the simplest linear control, when possible. In this paper, we use Mathematica. The technique is described next.
(1) Begin with an autonomous continuous dynamical system, ![]() ,
,![]() .
.
(2) Assume that the appropriate parameter values and initial conditions are known and the system exhibits chaos or hyperchaos at an equilibrium point![]() .
.
(3) Based on the known parameter values investigate a proportional controllerl of the form![]() ,
,![]() .
.
(4) If it is possible to find a proportional controller using the given constraints, the problem is solved.
(a) Linearize the controlled system ![]() at
at![]() .
.
(b) Compute the Jacobian, ![]() , of the controlled system. To determine the maximum value of the real part of the eigenvalues of
, of the controlled system. To determine the maximum value of the real part of the eigenvalues of![]() , try the following approaches that are well-suited to computer arithmetic.
, try the following approaches that are well-suited to computer arithmetic.
(i) Obtain bounds on the real part of ![]() using the Routh-Hurwitz theorem so that the maximum value of the real part of all eigenvalues of
using the Routh-Hurwitz theorem so that the maximum value of the real part of all eigenvalues of ![]() are negative, if possible.
are negative, if possible.
or
(ii) Compute the eigenvalues of ![]() and then determine conditions on
and then determine conditions on ![]() so that the maximum value of
so that the maximum value of
the real part of all eigenvalue is negative, if possible. Remark: Our simulations indicate that this yields better results than the Routh-Hurwitz theorem when the maximum value of the real part of the eigenvalues is close to 0.
(A) Given![]() , compute the eigenvalues of
, compute the eigenvalues of ![]() by computing the zeros of the characteristic polynomial of
by computing the zeros of the characteristic polynomial of![]() ,
,![]() .
.
(B) Find the real part of all zeros of![]() .
.
(C) Find conditions on ![]() so that the maximum value of the real part of all zeros of
so that the maximum value of the real part of all zeros of ![]() is negative, if possible.
is negative, if possible.
(5) Underlying Strategy: The “best” control is the simplest one. Thus, we start by searching for the simplest linear control possible.
For our case-studies we choose to numerically illustrate the techniques on versions of the Lorenz equations and Rössler attractors because they are well studied and because of their broad use in applications. Of course, a similar analysis can be carried out with many other high-dimensional dynamical systems that exhibit chaotic behavior, which we hope to do in future studies where we will focus on the underlying physical interpretation of the control.
3. The Lorenz Equations
The Lorenz system is a three-dimensional continuous nonlinear dynamical system,
![]() (2)
(2)
that has numerous applications in areas such as simple models of lasers, thermosyphons, and some chemical reactions.
Parameter ![]() (sometimes replaced by P) is known as the Prandtl number, and is usually fixed to be 10 in many studies. b is the Biot number, fixed to be 8/3. R is the Raleigh number, which is typically taken to be greater than 28. With these parameter values, the Lorenz system, (2), exhibits chaos for a wide range of initial conditions.
(sometimes replaced by P) is known as the Prandtl number, and is usually fixed to be 10 in many studies. b is the Biot number, fixed to be 8/3. R is the Raleigh number, which is typically taken to be greater than 28. With these parameter values, the Lorenz system, (2), exhibits chaos for a wide range of initial conditions.
For example, Figure 1 illustrates chaos in the Lorenz system using![]() ,
, ![]() ,
, ![]() and the initial conditions
and the initial conditions![]() ,
, ![]() , and
, and![]() . For these parameter values the Lorenz system has three equilibrium points
. For these parameter values the Lorenz system has three equilibrium points
![]()
The Jacobian of system (2) evaluated at each equilibrium point has the following eigenvalues
![]()
which shows that all three equilibrium points are unstable.
Using the described algorithm to try to find a control for an unstable equilibrium point, we choose an equilibrium point and search for the simplest control possible to stabilize it. To illustrate the concept, we choose
![]() . With this notation,
. With this notation, ![]() ,
, ![]() , and
, and ![]()
3.1. X-Control
We attempt to find the simplest control possible so search for an initial control of the form![]() ,
,
![]() (3)
(3)
Evaluated at![]() , the Jacobian of (3) is
, the Jacobian of (3) is
![]()
which has characteristic equation![]() , where
, where![]() ,
, ![]() , and
, and![]() . By the Routh-Hurwitz theorem, to guarantee that all the solutions of the characteristic equation have negative real part, we must have
. By the Routh-Hurwitz theorem, to guarantee that all the solutions of the characteristic equation have negative real part, we must have![]() ,
, ![]() , and
, and![]() . This occurs when
. This occurs when![]() . The system stabilizes faster as k increases. Figure 2 illustrates the stabilization using
. The system stabilizes faster as k increases. Figure 2 illustrates the stabilization using![]() .
.
With![]() ,
, ![]() ,
, ![]() , and
, and ![]() system (3) has equilibrium points
system (3) has equilibrium points
![]()
![]()
Figure 2. Stabilizing ![]() using the same initial conditions as in Figure 1.
using the same initial conditions as in Figure 1.
The Jacobian of system (3) evaluated at each equilibrium point has the following eigenvalues
![]()
Observe that the Jacobian confirms that ![]() is stable. Note that
is stable. Note that ![]() and
and ![]() are unstable.
are unstable.
This algorithm is well-suited to computer arithmetic and can be carried out at other equilibria. For example, rather than![]() , choose
, choose ![]() and a control of the form
and a control of the form ![]() in the X-equation results in
in the X-equation results in ![]() as illustrated in Figure 3.
as illustrated in Figure 3.
3.2. Y-Control
Generally, smaller k-values are considered “more efficient” than larger k-values. Thus, choosing ![]() but a control of the form
but a control of the form ![]() in the Y-equation results in
in the Y-equation results in![]() , which is more “efficient” than the linear control
, which is more “efficient” than the linear control ![]() in the X-equation used where we saw that
in the X-equation used where we saw that ![]() was required. Incorporating the linear control into the Y-equation, we find that
was required. Incorporating the linear control into the Y-equation, we find that ![]() stabilizes the system as illustrated in Figure 4.
stabilizes the system as illustrated in Figure 4.
However, the method illustrated is trial-by-error, which makes it particularly well-suited for computer arithmetic. For example, choosing ![]() and finding k-values for a control of the form
and finding k-values for a control of the form ![]()
in the Z-equation is impossible. In this case, the characteristic polynomial of the Jacobian evaluated at ![]() is
is![]() , which has zeros
, which has zeros![]() ,
, ![]() , and
, and![]() : for every value of k, the Jacobian evaluated at
: for every value of k, the Jacobian evaluated at ![]() has a positive eigenvalue so
has a positive eigenvalue so ![]() will be unstable.
will be unstable.
4. The Rössler Attractor
The three-dimensional version of the Rössler attractor is
![]() (4)
(4)
where a, b, and c are positive constants.
System (4) has been extensively studied and, consequently, its equilibria and the behavior of system (4) are well understood. Figure 5 illustrates chaos in the Rössler attractor using the parameter values ![]() and
and![]() . Wang and Wu, [6] , have applied a more complex controller than the one presented here to a four- dimensional hyperchaotic Rössler system.
. Wang and Wu, [6] , have applied a more complex controller than the one presented here to a four- dimensional hyperchaotic Rössler system.
For these parameter values, system (4) has the following equilibrium points
![]()
![]() (a) (b)
(a) (b)![]() (c) (d)
(c) (d)
Figure 5. Chaos in the Rössler attractor using “typical” parameter values and initial conditions, ![]() (a) t vs. x; (b) t vs y; (c) t vs z; (d) x vs y vs z.
(a) t vs. x; (b) t vs y; (c) t vs z; (d) x vs y vs z.
Following the same approach as in the previous example, we start by searching for a controller of the form ![]() and we choose to stabilize
and we choose to stabilize ![]() so that
so that![]() . Evaluated at
. Evaluated at![]() , the Jacobian of system (4) is
, the Jacobian of system (4) is
![]()
To guarantee that the eigenvalues of ![]() have negative real part, we apply the Routh-Hurwitz theorem. In this case we must have that
have negative real part, we apply the Routh-Hurwitz theorem. In this case we must have that![]() ,
, ![]() , and
, and![]() . These equations are satisfied when
. These equations are satisfied when ![]() . Observe that if we look at a plot of the maximum part of the real part of the roots of the characteristic polynomial,
. Observe that if we look at a plot of the maximum part of the real part of the roots of the characteristic polynomial, ![]() , of
, of![]() , we obtain the same interval as shown in Figure 6. Figure 7 illustrates stabilization using the k-value
, we obtain the same interval as shown in Figure 6. Figure 7 illustrates stabilization using the k-value![]() .
.
For this example, choosing to stabilize ![]() using a control of the form
using a control of the form ![]() in the Y-equation, where
in the Y-equation, where ![]() is the Y-component of
is the Y-component of ![]() is also successful. Using the same analysis, we find that
is also successful. Using the same analysis, we find that ![]() for
for![]() , 2, and 3 if
, 2, and 3 if![]() . Figure 8 illustrates stabilization using the k-value
. Figure 8 illustrates stabilization using the k-value![]() .
.
![]()
Figure 6. A plot of the maximum value of the real part of the zeros of ![]() as a function of k.
as a function of k.
It is not possible to stabilize the system using a control of the form ![]() in the Z-equation. The plot of the maximum value of the real part of the roots of the characteristic polynomial,
in the Z-equation. The plot of the maximum value of the real part of the roots of the characteristic polynomial, ![]() , of
, of![]() , in Figure 9 shows that the maximum value of the real part of any zero of
, in Figure 9 shows that the maximum value of the real part of any zero of ![]() is always positive.
is always positive.
5. High-Himensional Rössler Attractors
Using the same notation as Musielak and Musielak, [1] , the four dimensional Röseller system
![]() (5)
(5)
where a, b, c, and d are positive constants can exhibit more complex behavior than system (4). System (5) is interesting because depending upon the parameter values and initial conditions chosen, the system can exhibit hyperchaos, which is illustrated in Figure 10 using the parameter values![]() ,
, ![]() ,
, ![]() , and
, and![]() . On the other hand, adjusting the initial conditions can lead to dramatically different behavior as shown in Figure 11.
. On the other hand, adjusting the initial conditions can lead to dramatically different behavior as shown in Figure 11.
![]()
Figure 9. A plot of the maximum value of the real part of the zeros of ![]() as a function of k.
as a function of k.
For these parameter values, system (5) has the following equilibrium points
![]()
The Jacobian of system (5) evaluated at each equilibrium point has the following eigenvalues
![]()
so both ![]() and
and ![]() are unstable. We illustrate stabilizing
are unstable. We illustrate stabilizing ![]() . Keep in mind that we try to find the simplest linear control that stabilizes the system. For this system, it is not possible to stabilize
. Keep in mind that we try to find the simplest linear control that stabilizes the system. For this system, it is not possible to stabilize ![]() by incorporating a control of the form
by incorporating a control of the form ![]() into the X-equation because the Jacobian for the system
into the X-equation because the Jacobian for the system![]() ,
, ![]() ,
, ![]() , and
, and ![]() evaluated at
evaluated at ![]() has characteristic polynomial
has characteristic polynomial ![]() and the plot of the maximum value of the real part of any root of
and the plot of the maximum value of the real part of any root of ![]() shown in Figure 12 shows us that there is always a root with positive real part so
shown in Figure 12 shows us that there is always a root with positive real part so ![]() will be unstable. Similarly, it is not possible to stabilize
will be unstable. Similarly, it is not possible to stabilize ![]() by incorporating a control of the form
by incorporating a control of the form ![]() into the Y-equation, a control of the form
into the Y-equation, a control of the form ![]() into the Z-equation, or using a control of the form
into the Z-equation, or using a control of the form ![]() into the W-equation.
into the W-equation.
Next, we attempt using multiple controls. First, we try to find a control of the form ![]() in the X-equation and a control of the form
in the X-equation and a control of the form ![]() in the Y-equation but find that there are no
in the Y-equation but find that there are no ![]() and
and ![]() values that will stabilize the system with this control.
values that will stabilize the system with this control.
Next, we try to find a control of the form ![]() in the X-equation and a control of the form
in the X-equation and a control of the form ![]() in the Z-equation,
in the Z-equation, ![]() ,
, ![]() ,
, ![]() , and
, and![]() . Evaluated at
. Evaluated at ![]() the Jacobian of this system is
the Jacobian of this system is
![]()
Figure 12. A plot of the maximum value of the real part of the zeros of ![]() as a function of k.
as a function of k.
![]()
The characteristic polynomial of ![]() is
is![]() , where
, where
![]()
We plot the region where the maximum value of the real part of any zero of ![]() is negative in Figure 13 using the following algorithm.
is negative in Figure 13 using the following algorithm.
(1) Given ![]() and
and ![]() find the zeros of
find the zeros of![]() .
.
(2) Compute the real part of each zero and find the maximum real part of all zeros.
(3) Plot the region where the maximum value of the real part of any zero of ![]() is less than or equal to zero.
is less than or equal to zero.
We find that we can control the system and stabilize ![]() using
using ![]() and
and![]() . For these parameter values, the equilibrium points of the system are
. For these parameter values, the equilibrium points of the system are
![]()
The Jacobian of this system evaluated at each equilibrium point has the following eigenvalues
![]()
which shows us that ![]() is stable and
is stable and ![]() is unstable. Using the same initial conditions as those used in Figure 11, we see that using
is unstable. Using the same initial conditions as those used in Figure 11, we see that using ![]() and
and ![]() stabilize the system at
stabilize the system at ![]() in Figure 14. However, the stability of the equilibrium point
in Figure 14. However, the stability of the equilibrium point ![]() is not global as shown in Figure 15.
is not global as shown in Figure 15.
![]()
Figure 13. In the shaded region, the real part of all the zeros of ![]() are less than or equal to zero.
are less than or equal to zero.
6. Conclusion
In this paper, we have illustrated an elementary algorithm to find a linear control that can stabilize a high- dimensional continuous dynamical system that exhibits chaotic behavior. We demonstrate how the technique is implemented and that it is well-suited for computer arithmetic using the Lorenz equations and Rössler attractor
![]()
Figure 15. The control does not globally stabilize the system. The initial conditions are the same as those used in Figure 10.
as examples because they are very different models, but well studied and familiar to a wide audience. The simulations illustrated here show that the technique works on a wide range of dynamical systems, which we hope to further illustrate in later studies. Our simulations also indicate that it does not matter whether one uses the Routh-Hurwitz theorem or the characteristic polynomial to determined conditions on when all the eigenvalues of a matrix have negative real part. In future studies, we will focus on the physical interpretations of the controls that are introduced here as well as discuss conditions under which the control algorithm works or does not.
Computational Notes
The Mathematica, [7] , notebooks that the authors used to carry out the calculations as well as generate the figures here are available from the authors by sending a request to Jim Braselton at jbraselton@georgiasouthern.edu.