Transversality and the Stochastic Nature of Cash Flows

Lutz Kruschwitz, Andreas Löffler

Department of Finance, Accounting, and Taxation, School of Business and Economics, Freie Universitat Berlin, Berlin, Germany.

DOI: 10.4236/me.2015.66072                

Abstract

We show that a transversality condition is necessary when it comes to valuing a company with an infinite lifespan. Without transversality the firm value cannot be uniquely determined. Also, an assumption on a lower bound of cash flows is necessary to achieve the desired result. We discuss four different stochastic cash flow processes and analyze to what extent the processes associated with these enterprise values satisfy the transversality condition.

Keywords

Business Valuation, Stochastic Cashflows, Infinite Lifespan, Transversality

1. The Problem

When it comes to valuing firms, appraisers tend to assume that the companies in question will generate never- ending series of cash flows which cannot be forecasted with certainty. Both these assumptions (stochastic cash flows, infinite lifespan) lead directly to a fundamental problem which, to our knowledge, so far either has not been recognized or at least is not thoroughly discussed in the literature. In the following, we describe this problem and investigate how to resolve it. We also establish which approaches are slated for failure. Our paper helps to solve a hitherto apparently overlooked problem of business valuation.

To comprehensibly characterize the problem of interest, we start with a very simple observation and first consider a company with a finite lifespan that promises riskless future cash flows of at time. These cash flows are payments after firm taxes1 that will be distributed to the financiers, i.e., equity and debt holders. Using 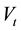for the firm’s market value at time t and 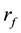for the riskless rate

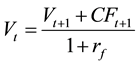(1)

must hold, providing that the market is free of arbitrage. Assuming a flat yield curve, continued insertion produces

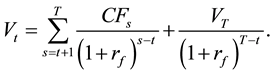(2)

Considering that a company only has value because it generates cash flows in the future, it follows that, assuming a finite lifespan, all cash flows beyond the lifespan vanish (i.e., for all 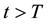we have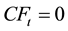) implying. This can be written as

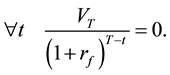(3)

Plugging this into (2) results in the well known valuation equation

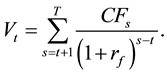
If we stick to risk-free cash flows but let the lifespan of the company be infinite, Equation (2) changes to

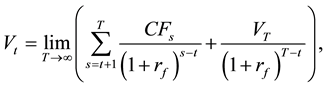
from which a valuation equation such as

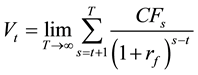
can be derived only if one assumes that the condition

(4)

holds. Since the denominator goes to infinity with a positive interest rate, the condition is only met if either remains finite or the numerator tends to infinity more slowly than the denominator.

The focus of our considerations is equations of the type (3) and (4) which we will refer to as transversality conditions. However, in the following, we analyze a realistic situation in which a company generates risky cash flows of 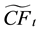at time t. The market value of the firm at time t is denoted by. is the riskless rate. The subjective probability that an investor assigns to the entry of future states is indicated by P. The information which the appraiser will have at time t is described by.2

Under the assumption that the capital market is arbitrage-free, the so-called fundamental theorem of asset pricing (FT) applies. It states that there exists a second and not necessarily unique probability measure Q such that

(FT)

holds. Q is also referred to as a risk neutral probability measure. The fundamental theorem of asset pricing is regularly and very successfully used in option pricing theory. Many derivative valuation models currently use this concept. Our further procedure is as follows:

First, we use an example to show that stochastic cash flows are conceivable that have startling characteristics. On the one hand, these cash flows satisfy the fundamental equation (FT), while on the other they do not necessarily comply with the popular valuation equation

(Val)

If one can construct such an example, it must be stated that the evaluation equation (Val) does not follow from the fundamental equation (FT) without employing further assumptions, or

It is advisable to take a close look at equation (Val). The conditional expectations represent

random variables. Hence, the right-hand side of equation (Val) constitutes the limit of a random variable.3 It is not at all clear how such a limit is defined, especially since in mathematics there are various ways to do so.4 Moreover, it is possible that one is dealing with stochastic cash flows that have no limit at all. This is exactly the case in our example.

In order to derive the valuation equation (Val) from the fundamental theorem of asset pricing (FT),

we need an additional assumption which we refer to as transversality and for which we provide a formally precise notation. We show that the transversality condition must be accompanied by a boundedness assumption. Surprisingly, this issue is seldom discussed in the literature.5 It should be mentioned that we develop further considerations that we elsewhere did years ago.6

We can and will show that the corporate values that satisfy both the fundamental equation and our transversality condition are unique. By contrast, there exist an infinite number of corporate values that meet only the fundamental equation but not the transversality condition.

If no lower bound exists, cases can arise in which the valuation equation (Val) applies yet the fundamental theorem of asset pricing (FT) does not. In these cases the boundedness assumption proves indispensable.7

Finally, we examine four prominent special cases involving stochastic cash flows and verify whether they meet both the transversality condition and the boundedness assumption.

The paper is organized as follows. First, we present the model, and then we discuss the above points systematically.

2. Model and Analysis

2.1. Model

We assume that there are no arbitrage opportunities in the capital market. Under this condition, there exists a risk-neutral probability measure Q. For the market value of a company whose cash flows can be duplicated on the capital market, the fundamental theorem of asset pricing (FT) applies.

The fundamental theorem also claims that both the subjective and the risk-neutral probability have the same zero sets.8 Accordingly, if we look at a subset of future events of the set of all possible future events, the probability under the subjective measure is zero if it vanishes under the risk-neutral probability measure, and vice versa:

The information (s-algebra) the appraiser expects to have at time t is denoted by. Now transversality shall be the requirement:

(Trans)

On page 757 we point out, in the context of a formally very similar term, that we are dealing with the limit of a random variable. If such a limit is required to go to zero, then first it has to be ensured that this limit exists, i.e., that convergence is given. Since mathematicians work with different types of convergence of random variables, a decision needs to be made. We decide in favor of almost-sure convergence, because this type of convergence is easiest to interpret; moreover, we are not able to derive the desired relationship between the fundamental theorem (FT) and the valuation equation (Val) by using a different concept of convergence. We state that a sequence of random variables converges to a random variable X if P-almost everywhere9

For simplicity, we also write. Since P and Q are equivalent, it makes no difference by what probability one measures the zero set.

We need yet another assumption that is more technical in nature. We must assume that the cash flows of the company cannot be arbitrarily negative. There is hence a value that we denote by K; we are aware that it falls short of the cash flows at any time and in any state:

Assumption 1. (Lower bound) There is a real number K such that the cash flows are P-almost everywhere greater than K,1⁰

(5)

A requirement such as this is frequently used in the literature on stochastic processes; see, e.g. ([7] , p. 139 f.).

To rule out that the company’s value goes beyond all limits, under certainty it is usually assumed that the cash flows do not grow above the discount rate. For the time being, we forego a corresponding assumption under uncertainty and return to the issue later.

Now we have formulated all the conditions required for our discussion, we show that the relationship between the fundamental theorem and the valuation equation is more complicated than may appear at first glance.

2.2. Analysis

2.2.1. Stochastic Cash Flows Which Can Not Be Evaluated

We present an example in which we show that there is (at least) one sequence of stochastic cash flows where indeed the fundamental theorem (FT) is true, but the valuation equation (Val) is not. If it is possible to construct examples like this, a connection of the following type

can not be derived without falling back on additional assumptions. This is where transversality comes into play. Our assertion is as follows:

Assertion 1. There is a series of stochastic cash flows such that (FT) is satisfied and (Val) does not apply.

Proof: A single example for which the claim turns out to be correct suffices to prove our assertion. To this end

we consider a progression with two accumulation points, e.g., and zero.1¹ Next we consider a sequence of iid random variables with a mean of. Now let a sequence of cash flows be defined as follows:

¹¹A progression like this can be constructed as follows. For arbitrary, we consider the divergent progression and use this to develop a new progression by following the instructions below:

Ÿ We start with. The sum amounts to.

Ÿ Then we let and. The sum now becomes negative.

Ÿ Now let to. Now the sum is.

Ÿ The next elements are added until the sum is negative or zero.

Ÿ After that, elements are added until the sum is greater than or equals.

This process can be continued indefinitely because the series was divergent. We thus obtain a sequence which permanently oscillates between the accumulation points and 0 and therefore cannot converge.

[1] ²This type of s-algebra is usually written in the form. If two random variables, X and Y, are independent, then is valid.

Let the discount rate be zero. We now verify whether the value of the company at according to equation (Val) can be calculated:

The limit does not exist. Based on our requirements, the following applies:

and we have constructed the series such that its limit does not exist. In this case there is no item that one could refer to as enterprise value.

However, it is possible to specify numerical values which meet the fundamental theorem simultaneously with the cash flows. These values are even certain quantities. To this end we let

and assume that is the s-algebra that is generated by the random variables. Now the fundamental theorem applies, since1²

Thus the property of our example is proven.

2.2.2. Fundamental Theorem, Transversality, and Evaluation

The that were chosen in the previous section obviously diverge and thus violate the transversality condition. We now prove our main result, which shows what role transversality plays in company valuation. The relationship may be illustrated graphically as follows:

Theorem 1. We assume a lower bound in accordance with assumption 1. Then the following two statements are equivalent:

1) For all cash flows and firm values both the fundamental theorem (FT) and the transversality condition (Trans) apply.

2) For all cash flows and firm values the evaluation equation (Val) is valid.

We also show the following:

Theorem 2. All corporate values that satisfy the fundamental theorem and the transversality condition are unique. However, there is always an infinite number of corporate values that satisfy only the fund- amental theorem (but not the transversality condition).

The last proposition clearly shows that the fundamental theorem alone is not sufficient to determine a unique firm value. If we assume only the fundamental theorem, there is an infinite number of variables that could be described as firm values. It is solely the transversality condition that enforces uniqueness.

Proof: We prove both statements jointly, starting with proposition 1.

It is quite easy to show that 2) follows from 1). From the fundamental theorem we obtain, by induction,

Taking the limit with, the second term vanishes. This leads trivially to 2).

To demonstrate that 1) follows from 2) requires more effort. Assuming that the evaluation equation (Val) is valid we must prove that necessarily both the fundamental theorem (FT) und and the transversality condition (Trans) must hold. We start with the fundamental theorem. For this purpose we note the evaluation equation both for and:

In the following we require the commutativity of limit and expectation (integral). For this we use Beppo Levi’s theorem of monotone convergence,1³ which implies that the discounted cash flows are non-negative. Yet our only assumption 1 is that the cash flows have a lower bound. To overcome this difficulty we consider modified cash flows, which are strictly positive by assumption 1. Levi’s theorem claims the commutativity of expectation and limit:

However, the commutativity is only valid for the modified cash flows, and we have yet to show that it is also valid for our non-modified cash flows. This can be accomplished as follows:

We recognize that the commutativity of the limit and the expectation under the assumptions made here for the original cash flows is given. Thus we finally have

which was to be proven.

We have yet to prove that transversality also applies. Since we have just shown that the fundamental theorem follows from the evaluation equation we may apply it and, by continuous exploitation of the recurrence relation, obtain

If we simultaneously assume that the valuation Equation (Val) holds, the second term in the above Equation must vanish. This was to be proven.

We now verify proposition 2. First, we show that the firm values are not unique without transversality. We assume a sequence of cash flows and a sequence of related corporate values. Then the new firm values

also satisfy the fundamental theorem for arbitrary. This can easily be verified:

We obtain a similar result when we add random variables with certain characteristics. If the random variables are iid and their expectation vanishes, then the items

also satisfy the fundamental theorem. For the following applies:

This was to be shown.

To prove that the corporate values are unique when the transversality condition is valid, we start from the premise that a sequence of uncertain cash flows generate two divergent firm values. From the fundamental theorem we then obtain

This yields the following, by induction:

Taking the limit produces

Due to transversality the right-hand side must disappear. This, however, contradicts the assumption, and exactly this was to be shown.

2.2.3. Necessity of a Lower Bound

Below, we show that one cannot give up the lower bound without fatal consequences. For we claim that:

Assertion 2. Without a lower bound in the sense of assumption 1 there are sequences of cash flows under which the evaluation equation holds yet the fundamental theorem is not satisfied.

[1] ⁴If one knows that holds, it is clear that this is indeed a probability measure.

Proof: The state space consists of all natural numbers. A state may have a probability1⁴

We now choose random variables, and for simplicity note only the conditional expectations with respect to the information available at time:

Obviously the cash flows are negative without limit, hence they apparently do not meet assumption 1. If we again assume that for the risk-free rate, the firm values are described by

We now calculate and to verify whether the fundamental theorem holds together with the definition of. We obtain

To determine, we calculate the finite sums and obtain

since other payments cancel out. In the limit, the random variable converges pointwise to

from which follows. Accordingly, we obtain

which is exactly what was to be shown.

3. Four Examples of Stochastic Cash Flows

So far we have refrained from more accurately specifying the sequences of stochastic cash flows that serve as a basis for company valuation. In the following, we propose four such specifications and verify in each case whether the boundedness assumption and transversality condition are satisfied. Should cost of capital come into play, let us assume that it is constant over time.

3.1. Additive Martingales

For this type of stochastic cash flow we assume that

(6)

[1] ⁵([13] , p. 1189 ff.).

¹⁶Since the random variables are independent the relation holds for (actually even for). Since the random variables are identically distributed, their expected value is independent of time s.

is true. This case was de facto examined by Froot and Obstfeld.1⁵

In this context are iid random variables with expectation.1⁶ For the case from (6) it follows that

(7)

The boundedness assumption according to (5) holds if the inequation

is valid for any T. This is true for non-negative random variables, for example.

Calculating the firm values using (Val) produces

Based on this we can examine whether the transversality condition (Trans) holds. We obtain

and observe that this term vanishes for any given t. In fact, the thus represent the corporate values for the additive cash flows that satisfy both the transversality and no arbitrage conditions.

3.2. Multiplicative Martingales (Autoregressive Cash Flows)

Now we assume that

(8)

[1] ⁷If the can take only two forms, a binomial tree is the result.

¹⁸See [14] .

¹⁹Due to both the characteristics of the conditional expectation and the independence of the random variable must hold. Since the random variable is identically distributed its expected value does not depend on t.

²⁰The growth factor g can even be time-dependent, which we do not want to assume here. See ([15] , p.~34).

^{2 [1]} ([15] , p. 39).

²²([15] , p. 37).

²³([14] , p. 328).

is true for the cash flows, where are iid random variables.1⁷ This case was de facto examined by Myers and Turnbull, although the authors presuppose the validity of a multi-period CAPM.1⁸ We do not require the restrictive assumptions underlying the CAPM and can show that the results of Myers and Turnbull are more general than the authors suggest.

If we denote the expected value of the random variable by

we obtain1⁹

In this case we speak of autoregressive cash flows.2⁰ We now suppose that the conditional expected returns k under the subjective probability measure P are deterministic and constant over time. Under this condition the following holds:2¹

(9)

Moreover, we show that the firm values satisfy2²

if is assumed.

Myers and Turnbull examine whether the valuation equation

that holds under certainty can be rewritten to

(10)

when uncertainty is present. To this end, they state the following: “It is plausible enough to replace the known with expected cash flows, and to add a risk premium to the discount rate. But these modifications lack rigorous support.”2³ On page 329 they state that one has to work very carefully in order as not to risk a flawed valuation Equation (10). However, if the conditions are met under which (9) is true, this is obviously no problem.

The question of whether a lower bound exists is easily answered. Assuming and, then follows directly and in Equation (5) holds.

To show conclusively that the transversality condition is satisfied, we compute

Due to this term vanishes for any given t, which corresponds to the assertion.

We can even prove that the firm value with is always finite, for we have

3.3. White Noise

We assume that the cash flows follow

(11)

where the are iid random variables with expectation g. For the corresponding corporate values we obtain

There is a lower bound when any is restricted. Obviously the transversality condition applies, too.

3.4. Mean-Reverting Cash Flows

There is empirical evidence that stochastic cash flows constantly revert to a mean.2⁴ Bhattacharya is one of the few authors to analyze this case theoretically.2⁵ We, too, consider in the following stochastic cash flows that are mean-reverting, i.e.,

(12)

Here, m represents the mean which the process tends to, and is the force with which this tendency is exerted in the model. For the return of the process to the mean is almost instantaneous and complete, while for there is only a very slow or weak return.

2⁶Notice that the mean reversion was formulated with the subjective and not the risk-neutral probability measure which will require some laborious calculations.

2⁷If the mean reversion is very pronounced, the first term disappears and the firm value becomes increasingly certain. This is not surprising since the cash flows themselves become increasingly certain and are practically equal to the mean.

²⁸See ([18] , Equation (9), p. 1321).

²⁹See [19] .

If we again assume deterministic and constant capital costs,2⁶ for the expected corporate value of the sub- sequent period we obtain

But since, with no arbitrage,

must apply, it follows

which can be rearranged to2⁷

(13)

Our result (13) corresponds to the one of Bhattacharya.2⁸ However, Bhattacharya needed the CAPM for his result, while we work without this model. Moreover, he applies the one-period CAPM to a multi-period problem which raises the problems that Fama discusses in detail.2⁹

The transversality condition is satisfied if

holds. The second term vanishes since the numerator does not depend on T. Therefore we must only show that

is valid. This requires some effort. First

applies and by using (13) we obtain

which can be simplified to

The repeated application of the last equation yields

or

Now it is evident that the transversality condition is satisfied if, since the second term disappears for any given t with.

Last, we turn to the existence of a lower bound. We prove this by induction and assume that applies. We must show that is also nonnegative. If and are assumed, then

holds, what was to be proven.

4. Conclusions

We show that firm values can not be derived solely from the fundamental theorem of asset pricing. Rather, a transversality condition must be added. A precise formulation of this condition is presented. Furthermore, a condition about the lower bound on cash flows could be shown as necessary.

We succeed in providing the appropriate firm values for four different types of stochastic cash flows. Table 1 summarizes our findings.

Table 1. Relationship between different types of stochastic cash flow and firm value.

Acknowledgements

We thank Dominica Canefield for many useful discussions. Without her assistance and permanent encouragement we would have overlooked some important issues.

NOTES

¹Taxes on the level of the company’s financiers are not considered.

²This is known as s-algebra, see ([1] , section 1.1, p. 15 ff.).

³Random variables remain random variables when multiplied with deterministic factors and then summed up.

⁴With random variables one can distinguish between pointwise convergence, convergence in quadratic mean, and convergence in probability; see ([2] , p. 48 ff. and 287 ff.).

⁵It is almost impossible to find any reference to transversality in standard textbooks. See, for example, [3] - [6] . Neither do the relevant journals offer a special analysis of the problem. Duffie mentions transversality precisely once, namely in the context of steady optimality problems, see ( [7] , p. 213). Cochrane is one of the few authors who addresses the issue in detail, see ( [8] , p. 25). Note that the first edition ( [9] , p. 27) had a typo in the transversality condition.

⁶See [10] [11] .

⁷Cochrane fails to notice this detail, see ( [8] , p. 24f.).

⁸A zero set is any subset of an event space with a probability of zero. Usually, this is referred to as an equivalent martingale measure and is sometimes written as P ~ Q.

⁹Meaning, the events for which the statement is not true are improbable.

¹⁰We do not assume that K is zero or even positive. The set of events with cash flows lower than K hence has a probability of zero, with respect to the subjective and, due to the equivalence of the martingale measure, also the risk-neutral probability measure.

[1] ³See ([12] , p. 115ff.).

2⁴See [16] [17] .

2⁵See [18] .

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Williams, D. (1991) Probability with Martingales. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511813658
[2]	Dudley, R.M. (2002) Real Analysis and Probability. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511755347
[3]	Berk, J. and DeMarzo, P. (2014) Corporate Finance. 3rd Edition, Pearson, Boston.
[4]	Brealey, R.A., Myers, S.C. and Allen, F. (2014) Principles of Corporate Finance. 11th Edition. McGraw-Hill, Irwin, New York.
[5]	Copeland, T.E., Weston, J.F. and Shastri, K. (2005) Financial Theory and Corporate Policy. 4th Edition, Addison-Wesley, Boston.
[6]	Ross, S.A., Westerfield, R.W. and Jaffe, J.F. (2013) Corporate Finance. 10th Edition, McGraw-Hill, Irwin, New York.
[7]	Duffie, D. (1988) Security Markets: Stochastic Models. Academic Press, Boston.
[8]	Cochrane, J.H. (2005) Asset Pricing. 2nd Edition, Princeton University Press, Princeton and Oxford.
[9]	Cochrane, J.H. (2001) Asset Pricing. Princeton University Press, Princeton and Oxford.
[10]	Kruschwitz, L. and Loffler, A. (1998) Unendliche Probleme bei der Unternehmensbewertung. Der Betrieb, 51, 1041-1043.
[11]	Kruschwitz, L. and Loffler, A. (2003) Zur Bewertung ewig lebender Unternehmen mit Hilfe von DCF-Verfahren. Der Betrieb, 56, 1401-1402.
[12]	Irle, A. (2005) Wahrscheinlichkeitstheorie und Statistik: Grundlagen, Resultate, Anwendungen. 2nd Edition, Teubner, Wiesbaden.
[13]	Froot, K.A. and Obstfeld, M. (1991) Intrinsic Bubbles: The Case of Stock Prices. The American Economic Review, 81, 1189-1214.
[14]	Myers, S.C. and Turnbull, S.M. (1977) Capital Budgeting and the Capital Asset Pricing Model: Good News and Bad News. The Journal of Finance, 32, 321-333. http://dx.doi.org/10.1111/j.1540-6261.1977.tb03272.x
[15]	Kruschwitz, L. and Loffler, A. (2006) Discounted Cash Flow: A Theory of the Valuation of Firms. Wiley, Chichester.
[16]	Graham, J.R. and Kim, H. (2009) The Effects of the Length of the Tax-Loss Carryback Period on Tax Receipts and Corporate Marginal Tax Rates. National Tax Journal, 62, 413-427. http://dx.doi.org/10.17310/ntj.2009.3.04
[17]	Forstemann, T. (2012) Folgen freie Cashflows unverschuldeter Unternehmen einem rein (schwach) autoregressiven Prozess? In: Abhandlungen zu aktuellen Fragen der Finanzwirtschaft, Kovac, Hamburg, 81-242.
[18]	Bhattacharya, S. (1978) Project Valuation with Mean-Reverting Cash Flow Streams. The Journal of Finance, 33, 1317-1331. http://dx.doi.org/10.1111/j.1540-6261.1978.tb03422.x
[19]	Fama, E.F. (1996) Discounting under Uncertainty. Journal of Business, 69, 415-428. http://dx.doi.org/10.1086/209698