A Form of Information Entropy

M. Divari, D. Vivona

Department of Basic and Applied Sciences for Engineering, Faculty of Civil and Industrial Engineering, “Sapienza” University of Rome, Roma, Italy.

DOI: 10.4236/ns.2014.617118                

Abstract

In this paper, by axiomatic way, a form of information entropy will be presented on crisp and fuzzy setting. Information entropy is the unavailability of information about a crisp or fuzzy event. It will use measure of information defined without any probability or fuzzy measure: for this reason it is called general information.

Keywords

Information, Entropy, Functional Equations, Fuzzy Sets

1. Introduction

The setting of entropy was statistical mechanics: in [1] Shannon introduced entropy of a partition 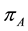of a set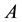, linked to a probability measure.

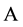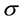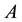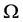Now, we recall this definition. Let be an abstract space, a -algebra of subsets of and 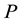a probability measure defined on. Moreover 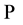is the collection of the partition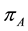, where

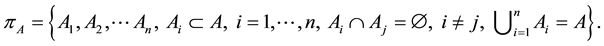
Basic notions and notations can be found in [2] . Setting 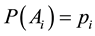with 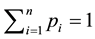(complete system),

Shannon’s entropy is

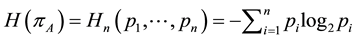
and it is measure of uncertainty of the system. Shannon’s entropy is the weight arithmetic mean, where the weights are. Many authors have studied this entropy and its properties, for example: J. Aczél, Daróczy, C. T. Ny; for the bibliography we refer to [3] [4] .

Another entropy was introduced by Rényi, called entropy of order,:

and it was used in many problems [5] [6] .

In generalizing Bolzmann-Gibbs statistical mechanics, Tsallis’s entropy was introduced [7] :

We note that all entropies above are defined through a probability measure.

In 1967 J. Kampé de Feriét and B. Forte gave a new definition of information for a crisp event, from axiomatic point of view, without using probability [8] -[10] . Following this theory other authors have presented measures of information for an event [11] . In [12] , with Benvenuti we have introduced the measure of information for fuzzy sets [13] [14] without any probability or fuzzy measure.

In this paper we propose a class of measure for the entropy of an information for a crisp or fuzzy event, without using any probability or fuzzy measure.

We think that not using probability measure or fuzzy measure in the definition of entropy of the information of an event, can be an useful generalization in the applications in which probablility is not known.

So, in this note, we use the theory explained by Khinchin in [15] and we give a new definition of entropy of information of an event. In this way it is possible to measure the unavailability of information.

The paper is organized as follows. In Section 2 there are some preliminaries about general information for crisp and fuzzy sets. The definitions of entropy and its measure are presented in Section 3. Section 4 is devoted to an application. The conclusion is considered in Section 5.

2. General Information

Let be an abstract space and the -algebra of crisp sets General information for crisp sets [8] [10] is a mapping

such that:

1)

2),

In analogous way [12] , the definition of measure of general information was introduced by Benvenuti and ourselves for fuzzy sets. Let be an abstract space and the -algebra of fuzzy sets. General information is a mapping

such that:

1)

2),

3. General Information Entropy

Using general information recalled in Section 2, in this paragraph a new form of information entropy will be introduced, which will be called general information entropy. Information entropy means the measure of un- availability of a given information.

3.1. Crisp Setting

In the crisp setting as in Section 2, given information the following definition is proposed.

Definition 3.1. General information entropy for crisp sets is a mapping with the following properties:

1) monotonicity:

2) universal values:

The universal values can be considered a consequence of monotonicity.

So, general information entropy is a monotone, not-increasing function with and

. Assigned information on, the function, is an example of

general information entropy.

It is possible to extend the definition above to fuzzy sets.

3.2. Fuzzy Setting

Given as in Section 2, the following definition is considered.

Definition 3.2. General information entropy for fuzzy sets is a mapping with the following properties:

1) monotonicity:

2) universal values:

The universal values can be considered a consequence of monotonicity.

So, general information entropy is a monotone, not-increasing function with and

Assigned information on an example of this entropy is,.

4. Application to the Union of Two Disjoint Crisp Sets

In this paragraph, an application of information entropy will be indicated: it concerns the value of information entropy for the union of two disjoint crisp sets. The procedure of solving this problem is the following: first, the presentation of the properties, second the translation of these properties in functional equations, by doing so, it will be possible to solve these systems [16] .

It is possible to extend this application also to the union of two disjoint fuzzy sets.

On crisp setting as in Section 2, let and two disjoint sets. In order to characterize information entropy of the union, the properties of this operation are used. The approach is axiomatic. The properties used by us are classical:

(u₁)

(u₂)

(u₃) as and,

(u₄)

(u₅)

Information entropy of the union is supposed to be dependent on and

(1)

where

Setting:, , , , with the properties lead to solve the following system of functional equations:

We are looking for a continuous function as an universal law with the meaning that the equations and the inequality of the system must be satisfied for all variables on every abstract space satisfying to all restrictions.

Proposition 4.1. A class of the solutions of the system is

(2)

where is any continuous bijective and strictly decreasing function with and

Proof. The proof is based on the application of the theorem of Cho-Hsing Ling [17] about the representation of associative and commutative function with the right element (here it is) as unit element.

From (1) and (2) information entropy of the union of two disjoint set is expressed by

where is any continuous bijective and strictly decreasing function with and

5. Conclusion

By axiomatic way, a new form of information entropy has been introduced using information theory without probability given by J. Kampé De Fériet and Forte. For this measure of information entropy, called by us, general because it doesn’t contain any probability or fuzzy measure, it has been given a class of measure for the union of two crisp disjoint sets.

Funding

This research was supported by research center CRITEVAT of “Sapienza” University of Roma and GNFM of MIUR (Italy).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Shannon, C. and Weaver, W. (1949) The Mathematical Theory of Communication. University of Illinois Press, Urbana.
[2]	Halmos, P.R. (1965) Measure Theory. Van Nostrand Company, New York.
[3]	Aczél, J. (2004) Entropies, Characterizations, Applications and Some History. Proceedings of IPMU-2004, Perugia, 4-9 July 2004, 1825-1830.
[4]	Aczél, J. (1969) Probability and Information Theory. Lectures Notes in Mathematics, 89. Springer-Verlag, Berlin, 1-11.
[5]	Rényi, A. (1961) On Measures of Entropy and Information. Proceedings IV Berkeley Symposium on Mathematical Statistics and Probability, 1, 547-561.
[6]	Rényi, A. (1970) Probability Theory. Nord Holland/Elsevier, Amsterdam, New York.
[7]	Tsallis, C. (1988) Possible Generalization of Bolzmann-Gibbs Statistics. Journal of Statistical Physics, 52, 479-487. http://dx.doi.org/10.1007/BF01016429
[8]	Forte, B. (1969) Measures of Information: The General Axiomatic Theory. RAIRO Informatique Théorique et Applications, R3, 63-90.
[9]	Forte, B. (1970) Functional Equations in Generalized Information Theory. In: Cremonese, Ed., Applications of Functional Equations and Inequalities to Information Theory, Roma, 113-140.
[10]	Kampé de Fériet, J. and Forte, B. (1967) Information et Probabilité. Comptes Rendus de l’Académie des Sciences Paris, 265, 110-114, 142-146, 350-353.
[11]	Kampé de Feriét, J. and Benvenuti, P. (1969) Sur une classe d’informations. Comptes Rendus de l’Académie des Sciences Paris, 269, 97-101.
[12]	Benvenuti, P., Vivona, D. and Divari, M. (1990) A General Information for Fuzzy Sets. Uncertainty in Knowledge Bases, Lectures Notes in Computer Sciences, 521, 307-316. http://dx.doi.org/10.1007/BFb0028117
[13]	Zadeh, L.A. (1965) Fuzzy Sets. Information and Control, 8, 338-353. http://dx.doi.org/10.1016/S0019-9958(65)90241-X
[14]	Klir, G.J. and Folger, T.A. (1988) Fuzzy Sets, Uncertainty and Information. Prentice-Hall International Editions, Englewood Cliffs.
[15]	Khinchin, A.Y. (1957) Mathematical Foundation of Information Theory. Dover Publications, New York.
[16]	Aczél, J. (1966) Lectures on Functional Equations and Their Applications. Academic Press, New York.
[17]	Ling, C.H. (1995) Representation of Associative Functions. Publicationes Mathematicae Debrecen, 12, 189-212.