Playing against Hedge

Miltiades E. Anagnostou¹, Maria A. Lambrou²

¹School of Electrical and Computer Engineering, National Technical University of Athens, Athens, Greece.
²Department of Shipping, Trade and Transport, University of the Aegean, Chios, Greece.

DOI: 10.4236/ijcns.2014.712050                

Abstract

Hedge has been proposed as an adaptive scheme, which guides the player’s hand in a multi-armed bandit full information game. Applications of this game exist in network path selection, load distribution, and network interdiction. We perform a worst case analysis of the Hedge algorithm by using an adversary, who will consistently select penalties so as to maximize the player’s loss, assuming that the adversary’s penalty budget is limited. We further explore the performance of binary penalties, and we prove that the optimum binary strategy for the adversary is to make greedy decisions.

Keywords

Hedge Algorithm, Adversary, Online Algorithm, Greedy Algorithm, Periodic Performance, Binary Penalties, Path Selection, Network Interdiction

1. Introduction

The problems of adaptive network path selection and load distribution have often been considered as games that are played simultaneously and independently by agents controlling flows in a network. A possible abstraction of these and other related problems is the bandit game. In the multi-armed bandit game [1] a player chooses one out of 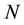strategies (or “machines” or “options” or “arms”). A loss or penalty (or a reward, which can be modeled as a negative loss) 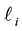is assigned to each strategy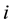 after each round of the game.

An agent facing repeated selections will possibly try to exploit the so far accumulated experience. A popular algorithm that can guide the agent in each selection round is the multiplicative updates algorithm or Hedge. In this paper we calculate the worst possible performance of Hedge by using the adversarial technique, i.e. we investigate the behavior of an intelligent adversary, who tries to maximize the player’s cumulative loss. In Section 1 we describe Hedge; in Section 2 we give a rigorous formulation of the adversary’s problem; in Section 3 we give a recursive solution; and in Section 4 we present sample numerical results. Finally, in Section 5 we explore binary adversarial strategies. Our main result is that the greedy adversarial strategy is optimal among binary strategies.

1.1. The bandit game

In a generalized bandit game the player is allowed to play mixed strategies, i.e. to assign a fraction (such

that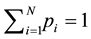) of the total bet to option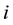, thereby getting a loss equal to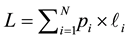. Alternatively,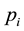

can be interpreted as a probability that the player assigns the bet on option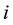. In the “bandit” version only the total loss is announced to the player, while in the “full information” version the penalty vector

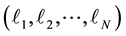is announced.

A game consists of rounds; a superscript marks the 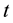th 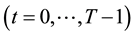round. Apparently the

player will try to minimize the total cumulative loss

(1)

by controlling the bet distribution, i.e. by properly selecting the variables. We use the additional assumption

that the loss budget is limited in each round by setting the constraint. Clearly a player’s goal is to

minimize his or her total cumulative loss. An extremely lucky player, or a player with “inside information”, would select the minimum penalty option in each round and would put all his or her bet on this option, thereby

achieving a total loss equal to.

1.2. The Hedge algorithm

Quite a few algorithmic solutions, which will guide the player’s hand in the full information game, have appeared in the literature. Freund and Schapire have proposed the Hedge algorithm [2] for the full information game. Auer, Cesa-Bianchi, Freund and Schapire have proposed the Exp3 algorithm in [3] . Allenberg-Neeman and Neeman proposed a Hedge variant, the GL (Gain-Loss) algorithm, for the full information game with gains and losses [4] . Dani, Hayes, and Kakade have proposed the GeometricHedge algorithm in [5] , and a modifi- cation was proposed by Bartlett, Dani et al. in [6] . Recently Cesa-Bianchi and Lugosi have proposed the ComBand algorithm for the bandit version [7] . A comparison can be found in [8] .

Hedge maintains a vector of weights, such that (, and

). In each round Hedge chooses the bet allocation according to the normalized weight

. When the opponent reveals the loss vector of this round, the next round weight is

determined so as to reflect the loss results, i.e. for some fixed, such that.

In [9] Auer, Cesa-Bianchi, Freund and Schapire have proved that the expected Hedge performance and the

expected performance of the best arm differ at most by. Freund and Schapire [2] have given a

loss upper bound, which relates the total cumulative loss with the total loss of the best arm.

1.3. Competitive analysis

The competitive analysis of an algorithm, which in this paper is Hedge, involves a comparison of’s performance with the performance of the optimal offline algorithm. In the bandit game the optimal offline algorithm, i.e. the optimal player’s decisions given the sequence of all penalties in advance, is trivial. In a given round the player can just bet everything on the option with the lowest penalty.

According to S. Irani and A. Karlin (in Section 13.3.1 of [10] ) a technique in finding bounds is to use an “adversary” who plays against and concocts an input, which forces to incur a high cost. Using an adversary is just an illustrative way of saying that we try to find the worst possible performance of an online algorithm. In our analysis the adversary tries to maximize Hedge’s total loss by controling the penalty vector (under a limited budget).

1.4. Interpretations and applications

In this section we offer some interpretations from the areas of 1) communication networks and 2) transportation. The general setting of course involves a number of options or arms, which must be selected by a player without any knowledge of the future.

Bandit models have been used in quite diverse decision making situations. In [11] He, Chen, Wand and Liu have used a bandit model for the maximization of the revenue of a search engine provider, who charges for advertisements on a per-click basis. They have subsequently defined the “armed bandit problem with shared information”; arms are partitioned in groups and loss information is shared only among players using arms of the same group. In [12] Park and Lee have used a multi-armed bandit model for lane selection in automated highways and autonomous vehicles traffic control.

1.4.1. Traffic load distribution

This first application example can take multiple interpretations, which always involve a selection in a compe- titive environment, in which competition is limited. It can be seen as 1) a path selection problem in networking, 2) a transport means (mode) choice or path selection problem, 3) a computational load distribution problem, which we mention in the end of this section. Firstly, we describe the problem in the context of networking.

Consider similar independent paths (in the simplest case just parallel links), which join a pair of nodes,. A traffic volume equal to is sent from to in consecutive time periods or rounds by

a population of agents. is the same in each round, but the allocation of to paths, i.e.

such that, is different in each round. An agent produces a constant amount of traffic equal

to, such that, in consecutive rounds, and allocates a part equal to to the th

path in round. The average delay (or cost) experienced by’s traffic in the th round is proportional to

, if we assume a linear delay (or cost) model. Linear models are used for simplicity in network analysis

[13] and can be realistic if a network resource still operates in the linear region of the delay vs. load curve, e.g. when delay is calculated in a link, which operates not very close to capacity. Agent aims at minimizing the total delay for its own traffic and may use Hedge to determine the quantities in round, assuming that knows the performance of its own traffic in each path in the past time period. Note that the maximum delay in a round occurs if puts the whole in a single path together with the whole traffic of the competition, i.e. with; then’s average delay in this round equals. On the contrary, if is evenly distributed in all paths,’s allocation decision does not really matter, as the average will be equal to

. Of course the minimum delay in a round will occur if puts the whole in an

empty path, thereby achieving a zero delay.

The above problem can also be formulated as a more general problem of distributing workload over a collection of parallel resources (e.g. distributing jobs to parallel processors). A. Blum and C. Burch have used the following motivating scenario in [14] : A process runs on some machine in an environment with machines in total. The process may move to a different machine at the end of a time interval. The load, which will be found on a machine at time round is the penalty felt by the process.

1.4.2. Interdiction

Although an adversary is usually a “technical” (fictional) concept, which serves the worst case analysis of online algorithms, in some environments a real adversary, who intentionally tries to oppose a player, does exist. An example is the interdiction problem.

We present a version of the interdiction problem in a network security context. An attacker attacks resources (e.g. launches a distributed denial of service attack on nodes, servers, etc., see [15] ) by sending

streams of harmful packets to resource at a rate (where and is constant). A defen-

der assigns a defense mechanism of intensity (e.g. a filter that is able to detect and avoid harmful packets with a probability proportional to) to resource. At the end of a time interval, e.g. one day, both the attacker and the defender revise the flows and the distribution of defense mechanisms to resources respectively, based on past performance.

Similar interpretations exist in transportation network environments, as in border and custom control, including illegal immigration control. An interdiction problem formulation can be used in a maritime transport security context: pirates attack the vessels traversing a maritime route. In [16] Vanek et al. assign the role of the player to the pirate. The pirate operates in rounds, starting and finishing in his home port. In each round he selects a sea area (arm) to sail to and search for possible victim vessels. A patrol force distributes the available escort resources to sea areas (arms), and pirate gains are inversely proportional to the strength of the defender’s forces on this area. Naval forces reallocate their own resources to sea areas.

2. Problem formulation

In this paper we aim at finding the worst case performance of Hedge. Effectively, we try to solve the following problem:

Problem 1. Given a number of options, an initial normalized weight vector, and a

Hedge parameter, find the sequence, , , that maximizes the player’s total cumulative loss

(2)

where is the penalty vector in round , such that, and the th

round penalty weights are updated according to

(3)

for and.

Clearly the objective function (2) is a function of a) the initial weights, and b) the variables

, and c). Due to the normalization of both weights and penalties there are indepen-

dent variables in total. In the following we use or

instead of whenever it is necessary to refer to these variables.

3. Recursion

Assuming that a given round starts with weights and the adversary generates penalties

, the next round will will start with weights where

(4)

Then, the total loss of a round game, which starts with weights, can be written as the sum of the losses of a single round game, which starts with weights, and a round game, which starts with

weights, as follows:

(5)

Note that the term, which expresses the contribution of the last rounds, depends only on the updated weights provided by the initial round. Such a Markovian property can be generalized in the following sense: A round game can be seen as consisting of a round game followed by a round game, whose initial weights are the final weights of, and no more details about are passed to.

Assuming that the solution to Problem 1 is the following recursive

formula for can be derived from (5):

(6)

where is the penalty vector chosen by the adversary in the initial round.

The optimal penalties can be computed also recursively. Let, where

denotes the th optimal penalty of the th option in the th round of a round game (starting

with weights). The optimal penalty of the initial round is apparently equal to the value of, which optimizes (6). Therefore

(7)

In all other rounds the optimal penalties are such that the total loss of the rest of the game is

maximized, i.e. such that is achieved. Since the total loss is achieved by

using penalties, the total loss is realized by using

instead. Therefore

(8)

4. Two option games and numerical results

this section we exploit the recursive methodology, which has been presented in the previous section, in order to provide some numerical results for two option games. We compare these results with available bounds in the literature. We consider, i.e. two option games. We keep only the independent penalties in the

extended notation and use the more compact version. As an example, the loss of a

single round game is given by

(9)

Also, since the initial weights are, we simplify the maximum cumulative loss to

. Assuming losses and, the next round will will start with weights and

, where

(10)

Then (6) is simplified to

(11)

where is the penalty chosen by the adversary for the first option in the initial round.

The iteration starts from, i.e. the loss of a single round game. In such game the adversary controls a

single penalty variable, as the loss is given by (9). Apparently the adversary will choose binary values, i.e.

if , and the maximum total loss is, i.e.

(12)

The graph of appears as the lowest V-shaped “curve” in Figure 1. The fact that the is a

piecewise linear function of with a breakpoint (i.e. a sudden change in its slope), creates even more break-

points in, and so on. Therefore, while it is possible to use the aforementioned recursion in

Figure 1. Plot of (maximum loss in a round game) vs. for and.

order to find analytical expressions for the maximum total loss and the associated penalties, the analysis becomes quite complicated even for small values of the number of rounds (i.e. in a round game). We omit this tedious analysis and present numerical results based on the recursive methodology given above.

Instead we have implemented a numerical computation based on (11). is approximated by

samples in the interval, i.e. by, where and. In the same way the

functions and are represented by samples and,

where. We have used. Initially we create by using (9). We

use the result as input to (11) and create. Then we use the already calculated and in (11)

to calculate, then and to calculate, and so on. In Figure 1 we show as a function of

the initial weight in games with up to ten rounds for different values of. Observe

that the shape of is more “interesting” for “unreasonably” small values of.

The optimal penalties can be determined by using formulas (7) and (8) for. In Figure 2 we draw one of the curves of Figure 1 together with the respective optimal penalties. The final round optimal penalty (i.e.

in this example) is certain to be binary, since the adversary will assign to the option with

the greatest weight factor. However, the penalties and of the first two games are clearly

non-binary.

5. Binary and greedy schemes

The penalty values in the first two rounds in the example of Figure 2 prove that the adversary’s optimal penalties are not necessarily binary. However, in this example is “unnaturally” close to 0, as in practical Hedge implementations is chosen close to 1; this choice achieves a more gradual adaptation to losses. Both experimental and analytical evidence show that the optimal penalties tend rapidly to binary values as approaches 1. Effectively, it seems that results very close to optimum can be achieved by a “binary adversary”, i.e. an adversary that will resort to binary values only.

On the other hand the optimal adversarial policy with binary penalties can be found exhaustively as

where is a set of binary vectors such that, i.e. only one component equals 1.

Apparently, the complexity of this calculation grows with. However, in the following we show that the optimal binary adversary is in fact the “greedy adversary”, The latter achieves binary optimality in linear time.

A “greedy adversary” is eager to punish the maximum weight option as much as possible in each round. Thus

Figure 2. Plot of (maximum total loss of a 4 round game) vs. for, together with the optimal penalties .

the adversary will assign exactly one unit of penalty to the maximum current weight option, and zero penalties to all other options. Given a sufficient number of rounds (say), it easy to see that the weights of an

option game are “equalized” so that any two weights, are such that for. When

equalization is achieved, a periodic phenomenon starts and the greedy penalties form a rotation scheme.

5.1. Greedy behavior

We explore the greedy pattern in a two option game that can easily be generalized to options. Assuming

initial weights, such that, a greedy adversary will choose

, iff, where (having assumed). At

the weight of the second option becomes for the first time greater than the weight of the first option, and a loss equal to 1 is assigned to the second option. Therefore, in the next step the weights (before normalization) are and, or equivalently and for the second time. In the next round they become and again, and in general they oscillate between these two pairs periodically. Therefore the total loss for in a pair of subsequent rounds is equal to

(13)

The value of is determined by the initially assumed inequality, and since ought to be integer

. The loss in the first steps is equal to

Therefore, for an even positive integer the total loss in steps is

In a game with more than two options it is straightforward to show that in the “steady” (periodic) state weights tend to become equal, i.e. almost equal to, where is the number of options. Consequently, the

loss is given by in a round game.

5.2. Optimality of the greedy behavior

The following proposition provides a simple polynomial solution to the problem of finding the optimal binary adversary.

Proposition 1. The greedy strategy is optimal for the adversary among all strategies with binary penalties. □

Proof: Due to normalization of weights and penalties, in the proof we mention only option 1 weights and penalties. Assuming an initial weight and penalties in the first rounds, the weight, which

emerges before the (n + 1)th round is, where. Effectively, two options are

available to the adversary in each step, either i) to assign a penalty equal to, which will produce an incre-

mental loss equal to, and will update the weight to or ii) to

assign a zero penalty, which will produce a loss equal to and an updated weight equal

to. Define.

This looks like a new game, in which the adversary is the player. The player’s status is determined by a real

number, and possible rewards are and. If the player opts for, this will bring him to

a new status. If he opts for, this will bring him to. In our case. Note also that

, , and. Moreover, if is the root of (or),

then for, and for. It is easy to prove that there is an odd symmetry

around, i.e., and is concave in, while it is

convex in.

Assume that, then, and. If the current status of the player is, and

, the greedy behavior is to move times to the right, which (unless is too short) will

bring the player to a point such that. If, then and the greedy

player must choose and move back to. Effectively, this starts an oscillation between

and, which will last until the end of the game. In the following we prove that this behavior is optimal, in spite of the fact that profits around are low.

The main idea behind this sketch of proof is that a retreat (with consequent low profits is never a

good investment for the future. Assume as the player’s status, and steps (rounds) remain until the end of

the game, while. The player executes forward steps, i.e., , with

rewards. Then, backward steps with gains are executed; consequently is

reached again. In the rest of the game, i.e. until the th step, greedy selections are made. This course of events is shown on curve (a) in Figure 3, where the dots mark the rewards achieved (and some dots have been vertically displaced by a small amount so as to be distinguishable from other dots at the same position). If greedy selections had been made all the way, the course of events would be as shown by curve (b).

If describes the status of the adversary on the greedy curve (b) at the th step and the status on curve

(a), then for. Furthermore,. Therefore the difference

between the cumulative reward on curve (b) and curve (a) is

Figure 3. Sample paths of player behavior, which are used in the proof of Proposition 1.

Effectively we need to show that. First, let us make some observations and explore other variations of. Note that, as given by (14), is positive if the cumulative reward from the back and forth movement (in the first steps) is less than the reward in the last steps. However, as increases, the position of the last step approaches and it can be shown that the cumulative reward of the last steps decreases. This property will be proved later, and it is due to the convexity and monotonicity properties of. When further increases, some of the very last steps of the greedy behavior enter the phase of oscillation around, and for sufficiently large, all belong to the oscillation phase. Note, however, that the oscillation phase rewards are those closer to 1/2, which is the lower limit of all greedy steps. If the greedy algorithm is to be optimal, even the oscillatory steps should bring a cumulative reward greater than the original back and forth movement. On the other hand, if we prove this last inequality, this will also prove (14), whose last steps bring more reward than the oscillatory steps.

Let be the pair of oscillation points around, i.e. and. In

the worst case, which has just been mentioned,

However, can be seen as the sum of terms, for

,. We shall further prove that each of these terms is smaller than the difference inside the big parentheses, i.e.

(14)

This is a consequence of the following lemma:

Lemma 1. For any concave function the following inequality is true:

(15)

Inequality (15) holds because

(16)

which is a consequence of the mean value theorem stating that there is a point in such that

. Also, there is a point in such that

. However, is a concave function, and its derivative is non-increa-

sing, therefore implies, which proves (16). In fact (15) can be

easily generalized to any same length intervals, even overlapping ones, i.e. if, then

(17)

Due to (15) each successive equal length (i.e.) interval produces an incremental reward

, which is smaller than the incremental reward of the next interval, and of all succeeding

intervals, as long as remains concave. Effectively, Lemma 1 proves that the incremental reward of the

rightmost interval, which does not contain, i.e. the interval, is the highest among the rewards

of all intervals of the same length, which begin to the left of. Unfortunately, our aim was to prove (14), which would be secured if remained concave in, e.g. if and. However this is

not true, since at turns from concave to convex. Fortunately, the term, which covers

the interval can be seen as the sum of rewards related with the concave in and the con-

cave in. Due to the odd symmetry around,

, therefore, and

.

However, due to the concavity of, , and

. Therefore

.

This result states that the interval, which contains, provides higher than the previous

interval, which in turn is higher than the of any previous interval of the same length.

Therefore we have seen so far that a sequence of penalties, which begins at some and involves one fold, can be reduced to a sequence without any folds, and with improved total reward, as shown in Figure 4. In Figure 4 a sequence of steps with a single fold, which starts at and ends at, is shown together with the

respective greedy sequence, which starts at and ends at. If the sequence must extend after

, the additional steps are oscillation steps around. The rest of this proof is just an application of this result, so that a sequence with an arbitrary number of folds can be reduced to an improved reward foldless sequence.

Figure 4. Reduction of a sequence of penalties, which contains a fold, to a sequence without folds and with improved total reward.

Suppose that the initial position of the game is at, and that (otherwise reverse the initial probabilities). Suppose also that the initial sequence does not extend beyond, i.e. it does not reach or it involves a number of oscillations around. Then take the last fold and reduce it as mentioned, i.e. by replacing it with an equal number of greedy steps at the end of the current sequence. If these steps reach, they are oscillation steps. Repeat the same step, until all folds have disappeared (oscillations do not count as folds). If the original sequence does extend beyond, the approach is the same, but the reader should note that the application of this algorithm will finally reduce the part, which extends beyond, to oscillations between and.

6. Conclusion

We summarize the main results of this paper: An worst performance (adversarial) analysis of the Hedge algorithm has been presented, under the assumption of limited penalties per round. A recursive expression has been given for the evaluation of the maximum total cumulative loss; this expression can be exploited both numerically and analytically. However, binary penalty schemes provide an excellent approximation to the optimal scheme, and, remarkably, the greedy binary strategy has been proved optimal among binary schemes for the adversary.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Robbins, H. (1952) Some Aspects of the Sequential Design of Experiments. Bulletin of the American Mathematical Society, 58, 527-535. http://dx.doi.org/10.1090/S0002-9904-1952-09620-8
[2]	Freund, Y. and Schapire, R.E. (1997) A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. Journal of Computer and System Sciences, 55, 119-139. http://dx.doi.org/10.1006/jcss.1997.1504
[3]	Auer, P., Cesa-Bianchi, N., Freund, Y. and Schapire, R.E. (2002) The Non-Stochastic Multi-Armed Bandit Problem. SIAM Journal on Computing, 32, 48-77. http://dx.doi.org/10.1137/S0097539701398375
[4]	Allenberg-Neeman, C. and Neeman, B. (2004) Full Information Game with Gains and Losses. Algorithmic Learning Theory: 15th International Conference, 3244, 264-278.
[5]	Dani, V., Hayes, T.P. and Kakade, S.M. (2008) The Price of Bandit Information for Online Optimization. In: Platt, J.C., Koller, D., Singer, Y. and Roweis, S., Eds., Advances in Neural Information Processing Systems, MIT Press, Cambridge, 345-352.
[6]	Bartlett, P., Dani, V., Hayes, T., Kakade, S., Rakhlin, A. and Tewari, A. (2008) High-Probability Regret Bounds for Bandit Online Linear Optimization. Proceedings of 22nd Annual Conference on Learning Theory (COLT), Helsinki.
[7]	Cesa-Bianchi, N. and Lugosi, G. (2012) Combinatorial Bandits. Journal of Computer and System Sciences, 78, 1404-1422. http://dx.doi.org/10.1016/j.jcss.2012.01.001
[8]	Uchiya, T., Nakamura, A. and Kudo, M. (2010) Algorithms for Adversarial Bandit Problems with Multiple Plays. In: Hutter, M., Stephan, F., Vovk, V. and Zeugmann, T., Eds., Algorithmic Learning Theory, Lecture Notes in Artificial Intelligence No. 6331, Springer, 375-389.
[9]	Auer, P., Cesa-Bianchi, N., Freund, Y. and Schapire, R.E. (1995) Gambling in a Rigged Casino: The Adversarial Multi-Armed Bandit Problem. Proceedings of 36th Annual Symposium on Foundations of Computer Science, Milwaukee, 322-331.
[10]	Hochbaum, D.S. (1995) Approximation Algorithms for NP-Hard Problems. PWS Publishing Company, Boston.
[11]	He, D., Chen, W., Wang, L. and Liu, T.-Y. (2013) Online Learning for Auction Mechanism in Bandit Setting. Decision Support Systems, 56, 379-386. http://dx.doi.org/10.1016/j.dss.2013.07.004
[12]	Park, C. and Lee, J. (2012) Intelligent Traffic Control Based on Multi-Armed Bandit and Wireless Scheduling Techniques. International Conference on Advances in Vehicular System, Technologies and Applications, Venice, 23-27.
[13]	Bertsekas, D.P. (1998) Network Optimization. Athena Scientific, Belmont.
[14]	Blum, A. and Burch, C. (2000) On-Line Learning and the Metrical Task System Problem. Machine Learning, 39, 35-88. http://dx.doi.org/10.1023/A:1007621832648
[15]	Cole, S.J. and Lim, C. (2008) Algorithms for Network Interdiction and Fortification Games. Springer Optimization and Its Applications, 17, 609-644. http://dx.doi.org/10.1007/978-0-387-77247-9_24
[16]	Vanëk, O., Jakob, M. and Pëchoucek, M. (2011) Using Agents to Improve International Maritime Transport Security. IEEE Intelligent Systems, 26, 90-95. http://dx.doi.org/10.1109/MIS.2011.23