Some Results on Wavelet Frame Packets

Sana Khan^*, Mohammad Kalimuddin Ahmad

Department of Mathematics, Aligarh Muslim University, Aligarh, India.

DOI: 10.4236/apm.2014.411069                

Abstract

The aim of this paper is to study wavelet frame packets in which there are many frames. It is a generalization of wavelet packets. We derive few results on wavelet frame packets and have obtained the corresponding frame bounds.

Keywords

Wavelet, Wavelet Packets, Frame Packets

1. Introduction

Let us consider an orthonormal wavelet of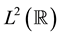. The orthonormal wavelet bases 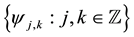have a frequency localization which is proportional to 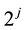at the resolution level. If we consider a bandlimited wavelet 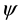(i.e. 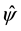is compactly supported), the measure of supp 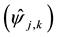is times the measure of supp, since

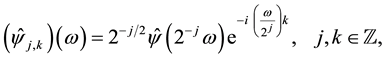
where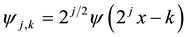. The wavelet bases have poor frequency localization when is large. For some applications, it is more convenient to have orthonormal bases with better frequency localization. This will be provided by the wavelet packets.

The wavelet packets introduced by Coifman, Meyer and Wickerhauser [1] [2] played an important role in the applications of wavelet analysis. But the theory itself is worthy for further study. Some developments in the wavelet packet theory should be mentioned, for instance Shen [3] generalized the notion of univariate orthogonal wavelet packets to the case of multivariate wavelet packets. Chui and Li [4] generalized the concept of orthogonal wavelet packets to the case of nonorthogonal wavelet packets. Yang [5] constructed a-scale orthogonal multiwavelet packets which were more flexible in applications. In [6] , Chen and Cheng studied compactly supported orthogonal vector-valued wavelets and wavelet packets. Other notable generalizations are biorthogonal wavelet packets [7] and non-orthogonal wavelet packets with r-scaling functions [8] . For a nice exposition of wavelet packets of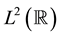, see [9] .

The main tool used in the construction of wavelet packets is the splitting trick [10] . Let 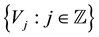be an MRA of 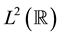with the corresponding scaling function 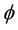and the wavelet. Let be the corresponding wavelet subspaces. In the construction of a wavelet from an MRA, the space is split into two orthogonal components and, where is the closure of the linear span of the func-

tions and and are the closure of the span of and respectively. Since, we see that the above procedure splits the half integer translates of a function into the integer translates of two functions.

We can also choose to split which is the span of. We

then have two functions whose translates will span the same space. Repeating the splitting procedure times, we get functions whose integer translates alone span the space. If we apply this to each, then the resulting basis of will give us a better frequency localization. This basis is called “wavelet packet basis”.

There are many orthonormal bases in the wavelet packets. Efficient algorithms for finding the best possible basis do exist; however for certain wavelet applications in signal analysis, frames are more suitable than orthonormal bases, due to the redundancy in frames. Therefore, it is worthwhile to generalize the construction of wavelet packets to wavelet frame packets in which there are many frames. The wavelet frame packets on was studied in [11] , and the frame packets on were studied by Long and Chen in [12] [13] . Also, multiwavelet packets and frame packets of were discussed in [14] .

Throughout the paper, the space of all square integrable functions on the real line will be denoted by and the inner product and Fourier transform of functions in is given by

and

respectively. Also the norm of any in will be denoted by and the relationship be-

tween functions and their Fourier transform is defined by. For, the

Fourier transform of is in and satisfies the Parseval identity. Also, let

be the collection of almost everywhere (a.e.) bounded functions, i.e., functions bounded everywhere except on sets of (Lebesgue) measure zero and equipped with the norm

2. Wavelet Packets and Wavelet Frame Packets

Definition 1. A multiresolution analysis (MRA) consists of a sequence of closed subspaces, of and a function, such that the following conditions hold:

1)

2) and.

3).

4)

5) is an orthonormal basis for.

The function is called the scaling function of the given MRA.

Suppose that generates a multiresolution analysis and that there exists some function in such that is the orthogonal complement of in. Then is called a basic wavelet relative to.

If is a basic wavelet relative to, then it is clear that the wavelet spaces generated by, satisfy the following properties:

6).

7).

8).

Since both the scaling function and the wavelet are in and is generated by, there exists two sequences and in such that

(1)

(2)

for all. For the Haar basis, we have

(3)

(4)

Therefore, for the Haar basis, the scaling function and the wavelet function satisfy the following recurrence equation

(5)

(6)

Due to Coifman, Meyer and Wickerhauser [1] [2] , we have the following sequences of functions

(7)

(8)

where and is the filter which satisfies the following properties

where is the Kronecker delta defined by

and

For in (7) and (8), we get

(9)

(10)

corresponds to our scaling function and corresponds to the wavelet. If we increase, we get the following structures

and so on. The functions, m = 2n or 2n + 1, n = 0, 1, 2, are called “wavelet packets” scaling to the scaling function. Thus, the family is a generalization of the wavelet

Definition 2. The family, is called a wavelet basis packet, where is the oscillation parameter, the scaling parameter and the translation parameter.

We can also write. The family constitutes wavelet frame packets if there are constants and, such that

(11)

3. Main Results

Define, , and

Consider

and

Theorem 1. Let be the basic wavelet packets such that

and

Then constitutes wavelet frame packets with frame bounds and.

Proof. Let be the class of all those functions such that and is compactly supported in. By using the Parseval identity, we have

Since, , we have

Hence,

(12)

Let for. Each is compactly supported in and belongs to. If is such a function,

which is -periodic and whose Fourier coefficients are, , then by Poisson sum formula we have,

Hence,

(13)

But the left side of (13) equals

(14)

It follows that

(15)

Applying (15) when in (12) we obtain

where,

In the expression for, the parameter is a non-zero integer. For each such there is a unique non- negative integer and a unique odd integer such that. Therefore, we have

Thus,

(16)

for all. By using Schwarz’s inequality we have

By changing variables in the second integral and using the fact that, and applying Schwarz’s inequality for series we have

Hence,

These inequalities together with (16) give us

.

Since is dense in, the above inequality holds for all.

Theorem 2. The system, is orthonormal if and only if

(17)

and

(18)

Proof. By using the Plancherel theorem we have

Thus, is orthonormal if and only if a.e. The converse is immediate. Performing a change of variables, we see that; this tells us that the system is orthonormal for each fixed when (17) is satisfied. The proof of condition (18) is similar.

Lemma 1. If is an orthonormal system, then

(19)

for all.

Proof. Let be the R.H.S of (19). We have to show that for a.e.. We first show that and then that; this will clearly give us (19). Using (18), with replaced by, we have

Replacing by, we have

This shows that Now, we calculate and show that. Changing variables in the sum over, we have

By using (17) and (18), we have

Theorem 3. Let be a sequence of wavelet frame packets with bounds and. Define by

(20)

If the numbers satisfy the two conditions

(21)

(22)

then defined by (20) is a wavelet frame packet with bounds and.

Proof. Let. Then

(23)

By Cauchy-Schwarz inequality, we get

On solving the second term in the last product, we have

Thus,

By (23), we have

Thus,

Similarly, one can prove the upper frame condition.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Coifman, R.R., Meyer, Y. and Wickerhauser, M.V. (1992) Wavelet Analysis and Signal Processing. In: Ruskai, M.B., et al., Eds., Wavelets and Their Applications, Jones and Barlett, Boston, 153-178.
[2]	Coifman, R.R., Meyer, Y. and Wickerhauser, M.V. (1992) Size Properties of Wavelet Packets. In: Ruskai, M.B., et al., Eds., Wavelets and Their Applications, Jones and Barlett, Boston, 453-547.
[3]	Shen, Z. (1995) Non-Tensor Product Wavelet Packets in . SIAM Journal on Mathematical Analysis, 26, 1061-1074. http://dx.doi.org/10.1137/S0036141093243642
[4]	Chui, C.K. and Li, C. (1993) Nonorthogonal Wavelet Packets. SIAM Journal on Mathematical Analysis, 24, 712-738. http://dx.doi.org/10.1137/0524044
[5]	Yang, S. and Cheng, Z. (2000) A-Scale Multiple Orthogonal Wavelet Packets. Mathematica Applicata, 13, 61-65. (In Chinese)
[6]	Chen, Q. and Cheng, Z. (2007) A Study on Compactly Supported Orthogonal Vector Valued Wavelets and Wavelet Packets. Chaos, Solitons and Fractals, 31, 1024-1034. http://dx.doi.org/10.1016/j.chaos.2006.03.097
[7]	Cohen, A. and Daubechies, I. (1993) On the Instability of Arbitrary Biorthogonal Wavelet Packets. SIAM Journal on Mathematical Analysis, 24, 1340-1354. http://dx.doi.org/10.1137/0524077
[8]	Feng, Z. and Chen, G. (2001) Nonorthogonal Wavelet Packets with r-Scaling Functions. Journal of Computational Analysis and Applications, 3, 317-330. http://dx.doi.org/10.1023/A:1012046206504
[9]	Hernandez, E. and Weiss, G. (1996) A First Course on Wavelets. CRC Press, Boca Raton. http://dx.doi.org/10.1201/9781420049985
[10]	Daubechies, I. (1992) Ten Lectures on Wavelets. SIAM, Philadelphia. http://dx.doi.org/10.1137/1.9781611970104
[11]	Chen, D. (2000) On the Splitting Trick and Wavelet Frame Packets. SIAM Journal on Mathematical Analysis, 31, 726-739. http://dx.doi.org/10.1137/S0036141097323333
[12]	Long, R. and Chen, W. (1997) Wavelet Basis Packets and Wavelet Frame Packets. Journal of Fourier Analysis and Applications, 3, 239-256. http://dx.doi.org/10.1007/BF02649111
[13]	Long, R. and Chen, W. (1995) Biorthogonal Wavelet Bases on . Applied Computational Harmonic Analysis, 2, 230-242. http://dx.doi.org/10.1006/acha.1995.1016
[14]	Behera, B. (2001) Multiwavelet Packets and Frame Packets of . Proceedings of the Indian Academy of Sciences (Mathematical Sciences), 111, 439-463. http://dx.doi.org/10.1007/BF02829617