On Diagnostics in Stochastic Restricted Linear Regression Models ()
1. Introduction
In a linear regression, the ordinary least squares estimator (LS) is unbiased and has minimum variance among all linear unbiased estimators and has been treated as the best estimator for a long time. When the addition of stochastic linear restrictions on the unknown parameter vector was assumed to be held, Theil [1] proposed the ordinary mixed estimator (OME). Hubert and Wijekoon [2] proposed the stochastic restricted Liu estimator (SRLE). And Li and Yang [3] introduced the stochastic restricted ridge estimator (SRRE) by grating the ORE into the mixed estimation procedure. Wu [4] discussed stochastic restricted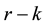 
class estimator and stochastic restricted 
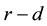class estimator in linear regression model. When the prior information and the sample information were not equally important, Schafrin and Toutenburg [5] introduced the method of weighted mixed regression and developed the weighted mixed estimator (WME). Li and Yang [6] grated the ORE into the weighted mixed estimation procedure and proposed the weighted mixed ridge estimator. Liu, et al. [7] proposed the stochastic weighted mixed almost unbiased ridge estimator by combining the WME and the AURE and also proposed the stochastic weighted mixed almost unbiased Liu estimator by combining the WME and the AULE in a linear regression model. He and Wu [8] proposed a new estimator to combat the multicollinearity in the linear model when there were stochastic linear restrictions on the regression coefficients. The new estimator is constructed by combining the ordinary mixed estimator (OME) and the principal components regression (PCR) estimator, which is called the stochastic restricted principal components (SRPC) regression estimator. Liu, Yang and Wu [9] introduced the weighted mixed almost unbiased ridge estimator (WMAURE) based on the weighted mixed estimator (WME) and the almost unbiased ridge estimator (AURE) in linear regression model. They discussed superiorities of the new estimator under the quadratic bias (QB) and the mean square error matrix (MSEM) criteria. Wu and Liu [10] considered several estimators for estimating the stochastic restricted ridge regression estimators. A simulation study has been conducted to compare the performance of the estimators. The result from the simulation study shows that stochastic restricted ridge regression estimators outperform mixed estimator.
Nearly forty years, the diagnosis and influence analysis of linear regression model has been fully developed (R.D. Cook and S. Weisberg [11] , Wei, et al. [12] ). Jiawei Wang [13] discussed the linear regression model with the random constraints, introduced its residuals and showed that the CDM was equivalent to the mean shift outlier model for diagnostics purpose based on general least square estimate. Lian Yang and Hu Yang [14] dealt with the data deleted model and the mean shift model under ellipsoidal restriction and obtained the equivalence of the diagonal statistic between the two models. Lu Wang [15] discussed the statistical diagnostic of multivariate linear regression model with linear restriction.
However, statistical diagnostics of stochastic restricted linear regression models based on stochastic restricted ridge estimator (SRRE) are studied in this paper. The paper is organized as follows. The model and the estimators are reviewed in Section 2. We show that the case deletion model is equivalent to the mean shift outlier model for diagnostic purpose in Section 3. Some diagnostic statistics are given in Section 4. The example to illustrate our results is given in Section 5.
2. Review of Stochastic Restricted Linear Regression Model
Consider the following linear model:
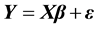, (1)
where 
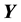is an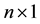 
vector of observation, 
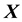is an 
design matrix of rank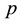
, 
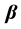is a 
vector denoting unknown coefficients, and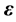 
is an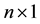 
random error vector with 
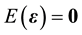and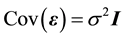
.
Suppose that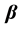 
satisfies the following stochastic restriction, that is,
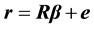, (2)
where ![]()
is a ![]()
nonzero matrix with ![]()
and ![]()
is a known vector, ![]()
and![]()
. In this paper, we assumed that ![]()
is independent of![]()
. And now model (1) is called stochastic restricted linear regression model.
2.1. Estimates of Model
Using the mixed approach, Durbin [16] , Theil and Goldberger [17] introduced the mixed estimator (ME), which is defined as follows:
![]()
. (3)
The mixed estimator is an unbiased estimator. However, when multicollinearity exists, the mixed estimator is no longer a good estimator.
Ozkale [18] proposed the following stochastic restricted ridge estimator (SRRE):
![]()
. (4)
The result from the simulation study shows that SRRE outperform ME (see Wu and Liu [19] ).
2.2. Estimating k
The most classical ridge estimator for linear regression is the following:
![]()
,
proposed by Hoerl and Kennard [20] , where ![]()
denote the maximum element of![]()
,
![]()
, ![]()
, and ![]()
is the estimator of![]()
. Hoerl, et al. [21] introduced
an alternative of the estimator of![]()
, which is defined as follows:
![]()
.
In Schaefer, et al. [22] , a modified version of this estimator is proposed as follows:
![]()
.
In Kibria, et al. [23] , a new estimator is proposed as follows:
![]()
.
This paper selects ![]()
to estimate ![]()
below.
3. Diagnostic Methods
3.1. Case-Deletion Model
Consider the stochastic restricted linear model, where the ![]()
-th case ![]()
is deleted,![]()
.
![]()
(5)
This model is called case-deletion model. Supposed that the SRRE of the coefficient function ![]()
in model (5) is![]()
.
In order to study the influence of the ![]()
-th case![]()
, and compare the difference between ![]()
and![]()
. The important result as following theorem.
Theorem 1. For model (5), the SRRE of ![]()
is
![]()
(6)
and
![]()
(7)
where![]()
,![]()
.
Proof: Let ![]()
and ![]()
corresponding to ![]()
and ![]()
to delete the cases which belong to![]()
. For model (5), we use the SRRE obtained that
![]()
Supposed that![]()
, ![]()
, then
![]()
which leads to (6).
Because
![]()
and![]()
,
hence
![]()
3.2. Mean Shift Outlier Model
The other common statistical diagnosis model is the mean shift outlier model (MSOM). For the stochastic restricted linear regression model, the corresponding MSOM is
![]()
(8)
where the parameter ![]()
are number, which describe the outlier. Let the SRRE of model (8) are ![]()
and![]()
. The corresponding matrix formula of model (8) as follows:
![]()
(9)
where![]()
, ![]()
is a n-dimensional vector, the ![]()
-th component is 1, and the other are zero.
Theorem 2. For model (8), there are![]()
, and![]()
.
Proof: By the matrix form of model (8), we obtained
![]()
On the other hand, by the formula of calculating the inverse matrix of partitioned matrix, we have
![]()
which leads to ![]()
and![]()
.
4. Diagnostical Statistics
4.1. Generalized Cook Distance
Let ![]()
is a nonnegetive matrix and ![]()
is one real number. The generalized Cook distance of the ![]()
-th case is defined as follows:
![]()
(10)
Theorem 3. Supposed that![]()
, then the generalized Cook distance of the ![]()
-th case is
![]()
where![]()
,![]()
.
Proof: Because
![]()
Substituting these results into (9) gives
![]()
4.2. W-K Statistic
W-K statistic is advanced from the view of data fitting. Considering the influence of the ![]()
-th case. In order to eliminate the influence of scale, it is also need to divide the variance of estimator![]()
. Because the keystone is to review the influence of deleting the ![]()
-th case. Hence, ![]()
is substituted by![]()
. Then, the W-K statistic can be expressed as follows:
![]()
(11)
4.3. Covariance Ratio Statistic
![]()
is to measure the superiorities of![]()
. The covariance ratio statistic is defined as follows:
![]()
,
which measure the influence of the ![]()
-th case.
5. Monte Carlo Experiments
In order to illustrate the validity of above results, extensive Monte Carlo sampling experiments were conducted. To evaluate the finite-sample performance of our proposed method, we simulate 60 random samples from the following model:
![]()
The stochastic restricts as follows:
![]()
where![]()
,![]()
. In order to checkout the validity of our proposed metho-
dology, we change the value of the first, 125th and 374th data. For every case, it is easy to obtain![]()
, ![]()
and![]()
.
From the Figure 1, Figure 2, Figure 3, we can see that in most cases, the value of are reasonably close to one fixed value. Following the definition and properties of diagnosis statistics, we can diagnose the strong influence points, the value of which deviate from the average seriously. Figure 2 and Figure 3 show that the first and the third data are strong influence points. Indeed, our results are illustrated.
6. Conclusion
In this paper, stochastic restricted linear regression models are revisited. Useful diagnostic methods are derived. Through simulation study, we illustrate that our proposed methods can work fairly well.