1. Introduction
Hazard rate functions can be used for several statistical analyses in medicine, engineering and economics. For instance, they are commonly used when presenting results in clinical trials involving survival data.
Several methods for hazard function estimation have been considered in the literature. Hazard function estimation by nonparametric methods has an advantage in flexibility because no formal assumptions are made about the mechanism that generates the sample order or the randomness. Estimators of the hazard function based on kernel smoothing have been studied extensively. For instance, see [1] -[5] .
The performance of the estimator at boundary points differs from the interior points due to so-called “boundary effects” that occur in nonparametric curve estimation problems; more specifically, the bias of the estimator at boundary points. To remove those boundary effects in kernel density estimation, a variety of methods have been developed in the literature. Some well-known methods are summarized below:
1) The reflection method [6] -[8] .
2) The local linear method [9] [10] .
In [11] this problem is solved by replacing the symmetric kernels by asymmetric Gamma kernel which never assigns weight outside the support.
A lot of people who care of estimation do many specific distributions, such as normal, log-normal, gamma and inverse-gamma distributions, and this makes us pose a question which is: is there any other distributions which can be used as a kernel in the estimation and then give us acceptable results?
In this paper, we propose the Weibull kernel which also never assigns weight outside the support. The Weibull distribution is a continuous probability distribution. It is named after Waloddi Weibull, who described it in detail in 1951, although it was first identified by Frchet (1927) and first applied by Rosin and Rammler (1933) to describe a particle size distribution.
This paper is organised in five sections. In the first section, we present some information about kernel smoothing, hazard functions and the proposed kernel. In the second section, we introduce some definitions and relations, and state the conditions under which the results of the paper will be proved. In the third section, we investigate the bias, variance and optimal bandwidth of the Weibull kernel estimator. In the fourth section, we investigate the asymptotic normality of the Weibull kernel estimator of the pdf and of the hazard function estimator. In the fifth section, the performance of the proposed estimator will be tested via two applications, simulated and real data.
2. Preliminaries
In this section, we state the conditions under which the results of the paper will be proved. Also, we mention the definition of gamma function and some relations related to it, then we will define Weibull kernel.
Conditions
1) Let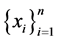 
be a random sample from a distribution of unknown probability density function f defined on 
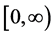such that f has a continuous second derivative.
2) 
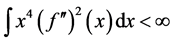and 
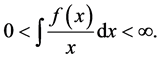
3)
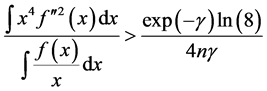, where 
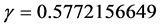is Euler’s constant.
4) h is smoothing parameter satisfying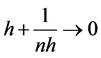 
as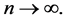 
The Gamma function is defined to be the improper integral:
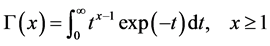
The Taylor expansion about zero of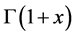 
and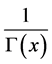 
is available and given by:
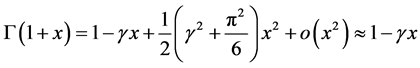
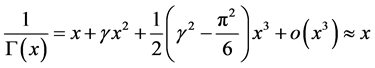
Also,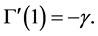 
On the other hand, notice that:
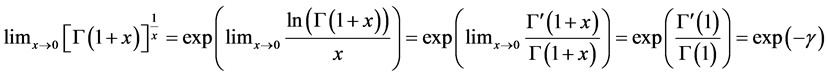
Moreover, the difference between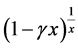 
and ![]()
gets small when![]()
, we can approximate ![]()
by![]()
.
In this paper we consider the following Weibull kernel function:
![]()
If a random variable Y has a pdf![]()
, then![]()
, and the variance is
![]()
We propose the following estimator of the probability density function![]()
, the Weibull estimator,
![]()
3. Bias, Variance and Optimal Bandwidth
Proposition 1.
The bias of the proposed estimator is given by:
![]()
(1.1)
Proof:
![]()
where ![]()
follows a Weibull distribution with scale parameter ![]()
and shape parameter![]()
, and from the expression of the mean and variance of Weibull distribution we deduce that the mean is ![]()
and![]()
.
The Taylor expansion about ![]()
for ![]()
is:
![]()
So, ![]()
![]()
(1.2)
Hence,
![]()
Proposition 2.
The variance of the proposed estimator is given by:
![]()
(1.3)
Proof:
![]()
where,
![]()
Using the transformation ![]()
we get:
![]()
Therefore,
![]()
where
![]()
and ![]()
follows as Weibull distribution with mean ![]()
and variance
![]()
The Taylor expansion of ![]()
is as follows:
![]()
So,
![]()
This implies that
![]()
Therefore,
![]()
Optimal Bandwidth:
First of all, we will define MSE and Mean Integrated Squared Error (MISE) as follows:
![]()
Therefore,
![]()
(1.4)
The Taylor expansion of 8h is given as follow:
![]()
Therefore, we can approximate MISE to be:
![]()
(1.5)
where, ![]()
and ![]()
We will now find the optimal bandwidth by minimizing (1.5) with respect to h, so we have
![]()
(1.6)
![]()
(1.7)
Setting (1.6) equal zero yields the optimal bandwidth ![]()
for the given pdf and kernel:
![]()
(1.8)
In addition, (1.7) proves that this value minimize (1.5). Substituting (1.8) for h in (1.5) gives the minimum MISE for the given pdf and kerne which is given by:
![]()
(1.9)
Note that ![]()
depend on the sample size n, the kernel and on the unknown pdf.
4. Asymptotic Normality
In this section, we state the main two theorems talking about the asymptotic normality for the proposed estimator and an important lemma which we will use in the second main theorem.
Definition 1. A hazard rate function is defined as the probability of an event happening in a short time interval. More precisely, it is defined as:
![]()
The hazard rate function can be written as the ratio between the pdf ![]()
and the survivor function ![]()
as follows:
![]()
The kernel estimator of ![]()
is ![]()
where,
![]()
Definition 2. We defined the proposed estimator for the hazard rate function to be:
![]()
Theorem 1. Under conditions 1, 2, and 3, the following holds
![]()
(1.10)
Proof:
Let![]()
,![]()
. Then![]()
, where ![]()
are independent and identically distributions (iid) and![]()
.
We show now that the Liapounov condition is satisfied, that is for some ![]()
![]()
First of all, we have:
![]()
where,![]()
. Then we have:
![]()
where, ![]()
follows a Weibull distribution with mean ![]()
and variance
![]()
.
The Taylor expansion of ![]()
about the mean ![]()
is as follows:
![]()
![]()
where ![]()
Therefore,
![]()
(1.11)
Now substituting ![]()
the following is hold:
![]()
Hence,
![]()
The last term vanishes as![]()
, since condition 4 implies that ![]()
and![]()
. Also, the remaining component of the last term are bounded from condition 2.
Lemma 1. Under conditions 1, 2 and 3 the following holds
![]()
(1.12)
Proof:
First of all, we have from the definition of ![]()
the following relations:
![]()
where ![]()
is defined as in Proposition 1. This implies that, ![]()
Therefore,
![]()
(1.13)
On the other hand, ![]()
can be written as follows:
![]()
where ![]()
Now, given![]()
, ![]()
, then we have:
![]()
The second term vanishes as ![]()
and![]()
, since from 1.2 we have
![]()
Further, by replacing ![]()
with ![]()
in (1.11) and assuming that
![]()
we have:
![]()
![]()
(1.14)
Since ![]()
then by (1.13) and (1.14), we have:
![]()
This complete the proof of the lemma.
Theorem 2. Under conditions 1, 2, and 3, the following holds
![]()
(1.15)
Proof:
![]()
Note that the second term vanishes by (1.12), and the first term is asymptotically normally distributed by (1.10).
Moreover, from (1.10) and (1.15) too we have:
![]()
Therefore,
![]()
and,
![]()
5. Applications
In this section, the performance of the proposed estimator in estimating the pdf and hazard rate function is tested upon two applications using a simulated and real life data.
5.1. A Simulation Study
A sample of size 200 from the exponential distribution with pdf ![]()
is simulated. We computed the bandwidth using the relation
![]()
(1.16)
see [8] page 47 and it equals (0.36658).
The density and the hazard functions were estimated using the Weibull estimator. The estimated values and the true exponential pdf are plotted in Figure 1(a), this figure shows that the performance of the Weibull estimator is acceptable at the boundary near the zero. In the interior the behavior of the pdf estimator becomes more similar as we get away from zero. Also Figure 1(b) shows that the performance of the Weibull estimator of the hazard function is acceptable at the boundary near the zero which we concern on. The mean squared error (MSE) of proposed estimator of the density function is equal to 0.0001393763 and for the hazard function is evaluated for the interval [0, 0.5]—because we concern about closest values to zero—and is equal to 0.0189427.
5.2. Real Data
In this subsection, we used the suicide data given in Silverman [8] , to exhibit the practical performance of the Weibull estimator. The data gives the lengths of the treatment spells (in days) of control patients in suicide study. We used the logarithm of the data to draw Figure 2(a) and Figure 2(b) using bandwidth equals 0.480411 which computed by (1.16), these figures exhibit the two estimated functions of the probability density and hazard rate functions, respectively.
6. Comment and Conclusion
In this paper, we have proposed a new kernel estimator of the hazard rate function for (iid) data based on the Weibull kernel with nonnegative support; we showed that the bias depends on the smoothing parameter h and the estimated point x, and it goes to zero as![]()
, also it gets small for the values of x closed to zero. The variance was investigated and we noticed that it depends also on h and x. On the other hand, it goes to zero as![]()
, and gets large at the values of x close to zero. Moreover, the optimal bandwidth and the asymptotic normality were investigated.
![]()
![]()
(a) (b)
Figure 1. (a) The Weibull kernel estimator of the density function; (b) The hazard rate function for the simulated data of the exponential distribution.
![]()
![]()
(a) (b)
Figure 2. (a) The Weibull kernel estimator of the density function; (b) The hazard rate function for the suicide data.
In addition, the performance of the proposed estimator is tested in two applications. In a simulation study using exponential sample we noticed that the performance of the proposed estimator is acceptable, and gives a small MSE.
Using real data, we exhibited the practical performance of the Weibull estimator.