A Fast Heuristic Algorithm for Minimizing Congestion in the MPLS Networks ()
2. Problem Description and Mathematical Models
We describe the problem in a more general case. In the minimum congestion k-splittable multi-commodity flow problem, a directed graph 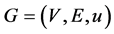 is given with
is given with  and
and , with arc capacities
, with arc capacities ,
, . A set of commodities is denoted by
. A set of commodities is denoted by , each commodity
, each commodity  has a certain amount of demand
has a certain amount of demand  to transmit, a source node
to transmit, a source node  and a destination node
and a destination node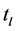 , and the number of paths that commodity
, and the number of paths that commodity  can use
can use . The goal is to find a flow
. The goal is to find a flow 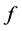 that satisfies all demands of the commodities and minimize the congestion: Find the smallest
that satisfies all demands of the commodities and minimize the congestion: Find the smallest  such that there exists a feasible flow satisfying the demands and the path restrictions if all capacities are multiplied by
such that there exists a feasible flow satisfying the demands and the path restrictions if all capacities are multiplied by . In [1] , we first propose two different mathematical models, namely the arc-path and arc-flow model. In this paper, we also use the two models to describe our problem.
. In [1] , we first propose two different mathematical models, namely the arc-path and arc-flow model. In this paper, we also use the two models to describe our problem.
2.1. The Arc-Path Model
Let  denotes the set of all paths of commodity
denotes the set of all paths of commodity ,
,  denotes the flow value on path
denotes the flow value on path  of commodity
of commodity ,
,  denoting whether or not path
denoting whether or not path  is used by commodity
is used by commodity .
.  denotes the maximum flow value that path
denotes the maximum flow value that path  can transmit.
can transmit.
This problem is formulated as follows:

 (1)
(1)
 (2)
(2)
 (3)
(3)
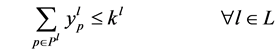 (4)
(4)
 (5)
(5)
 (6)
(6)
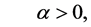 (7)
(7)
The objective function is to minimize the factor that each edge can multiply. The first constraints (1) ensure that the flow value on an edge  is at most
is at most 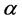 of its capacity,
of its capacity,  is a constant, if
is a constant, if ,
, 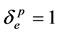 , otherwise
, otherwise . The constraints (2) ensure that each commodity's demand is satisfied, and constraints (3) indicate that only path
. The constraints (2) ensure that each commodity's demand is satisfied, and constraints (3) indicate that only path  is used by commodity
is used by commodity , that is
, that is , the flow value
, the flow value  can be non-negative. The notation
can be non-negative. The notation 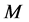 is any upper bound of the objective value, which can be selected by
is any upper bound of the objective value, which can be selected by  with
with . Constraints (4) limit the number of paths that a commodity can use. Constraints (5)-(7) force the variables to take on feasible values.
. Constraints (4) limit the number of paths that a commodity can use. Constraints (5)-(7) force the variables to take on feasible values.
2.2. The Arc-Flow Model
The variable  refers to the flow value of the
refers to the flow value of the  -th path of commodity
-th path of commodity  on edge
on edge ,
,  , and binary variable
, and binary variable  denotes whether or not edge
denotes whether or not edge  is used by the
is used by the  -th path of commodity
-th path of commodity . We use
. We use 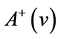 and
and  to denote the outgoing arcs and ingoing arcs of node
to denote the outgoing arcs and ingoing arcs of node , respectively. Then the arc-flow model is stated as follows:
, respectively. Then the arc-flow model is stated as follows:

 (8)
(8)
 (9)
(9)
 (10)
(10)
 (11)
(11)
 (12)
(12)
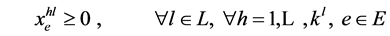 (13)
(13)
 (14)
(14)
 (15)
(15)
Constraints (8) ensure that each commodity’s demand is satisfied, and constraints (9) ensure the flow on each edge is at most  times of its capacity, constraints (10) indicate that only if edge
times of its capacity, constraints (10) indicate that only if edge  is used by the
is used by the 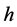 -th path of commodity
-th path of commodity  can the variable
can the variable 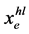 be positive. Constraints (11) are the flow conservation constraints and (12) are used to prevent cycles connecting to the
be positive. Constraints (11) are the flow conservation constraints and (12) are used to prevent cycles connecting to the  -th path of commodity
-th path of commodity  for each
for each ,
, . Constraints (13)-(15) force the variables to take on feasible values.
. Constraints (13)-(15) force the variables to take on feasible values.
The main difference of the two mathematical models is that in the arc-path model each commodity has a feasible path set which contains all the paths for the commodity in the network and we only need to select some paths from the path set to transmit the demand. Sometimes, determining all the feasible paths for a commodity is not an easy thing. While in the arc-flow model, the transmitting paths for each commodity are found in the network directly. We know that both of the above two formulations are mixed integer linear problems which are NP-hard to solve, especially when the size of the network increases, the number of paths in  grows exponentially, and it is impossible to obtain the exact solutions in short time.
grows exponentially, and it is impossible to obtain the exact solutions in short time.
We also note that the multi-source k-splittable problem cannot equally transform to the single-source k-splittable problem. If we add a super source node , connecting it to each source node
, connecting it to each source node 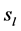 for
for , each edge
, each edge  has capacity
has capacity , then a feasible flow in the new graph with flow value
, then a feasible flow in the new graph with flow value  may not transform to a feasible flow satisfying all demands in the original graph. For example, a graph with five nodes
may not transform to a feasible flow satisfying all demands in the original graph. For example, a graph with five nodes , five edges
, five edges  with capacities 1, 4, 4, 4, 4, respectively. Two commodities with endpoints
with capacities 1, 4, 4, 4, 4, respectively. Two commodities with endpoints 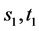 and
and 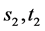 have demands 5 and 4, respectively. We add a super source node
have demands 5 and 4, respectively. We add a super source node  as mentioned above and a super sink node
as mentioned above and a super sink node . Add two edges
. Add two edges  and
and 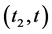 with capacity 5 and 4, respectively. Applying a maximum flow algorithm, such as the Edmonds-Karp Algorithm in [12] , we obtain a maximum flow
with capacity 5 and 4, respectively. Applying a maximum flow algorithm, such as the Edmonds-Karp Algorithm in [12] , we obtain a maximum flow  from
from  to
to  and edge flow values are as follows:
and edge flow values are as follows: ,
,  ,
,  ,
,  ,
,  ,
,  ,
, ,
,  and
and . We can note that
. We can note that  cannot transform to a flow in the original graph that satisfies the two commodities, since in
cannot transform to a flow in the original graph that satisfies the two commodities, since in  there is no path with positive flow value from
there is no path with positive flow value from  to
to 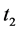 and the flow value from
and the flow value from  to
to  is only 1.
is only 1.
In this paper, for simplicity, we only consider the single-source multi-commodity k-splittable flow problem, denote the common source node by . We propose a heuristic algorithm which largely reduce the size of the path set
. We propose a heuristic algorithm which largely reduce the size of the path set  for each commodity
for each commodity  to a small path set
to a small path set , and solve the arc-path model with
, and solve the arc-path model with  replaced by
replaced by  for
for .
.
3. The Heuristic Algorithm
In this paper, we assume that there is a feasible splittable flow  that satisfies all the demands of the commodities. We know that
that satisfies all the demands of the commodities. We know that  may not meet all the path number restrictions of the commodities. In [1] , we find at most
may not meet all the path number restrictions of the commodities. In [1] , we find at most  paths for commodity
paths for commodity  from
from , and then reallocate flow to the unsatisfied commodities by solving a series of linear programming. In this paper, we also find paths for commodity
, and then reallocate flow to the unsatisfied commodities by solving a series of linear programming. In this paper, we also find paths for commodity  from
from . On the one hand, we finds paths for each commodity until the total path value is equal to its demand, on the other hand, for sake of fairness of different commodities, we find at most one path for each commodity in a round. The steps of the algorithm are as follows and the flow chart of the algorithm is presented in Figure 1.
. On the one hand, we finds paths for each commodity until the total path value is equal to its demand, on the other hand, for sake of fairness of different commodities, we find at most one path for each commodity in a round. The steps of the algorithm are as follows and the flow chart of the algorithm is presented in Figure 1.
Step 1: Find a feasible splittable flow  in
in  that satisfies all the demands; Initialize
that satisfies all the demands; Initialize  for all
for all , denoting the paths found from
, denoting the paths found from  for commodity
for commodity ;
;
Step 2: For , if the total path value of the paths in
, if the total path value of the paths in  is less than
is less than , find a path from the current flow
, find a path from the current flow for commodity
for commodity  that carry the largest flow value. Add the new path with its flow value to
that carry the largest flow value. Add the new path with its flow value to . Once a path is found, delete its flow from
. Once a path is found, delete its flow from , update the edge flow values in
, update the edge flow values in ;
;
Step 3: If there is some edge in  with positive flow value, go to step 2; otherwise, solve the arc-path model
with positive flow value, go to step 2; otherwise, solve the arc-path model

Figure 1. The flow chart of the heuristic algorithm. In the process of the algorithm, when the total path value already found for some commodity equals to its demand, we will not find paths for it in the next round.
with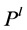 replaced by
replaced by .
.
Remarks:
● In step 1, we can add a super sink node  to
to , each sink node
, each sink node ,
,  is connected to
is connected to  with capacity
with capacity , denote the new graph by
, denote the new graph by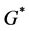 . Finding
. Finding  that satisfies all the demands of the commodities is equivalent to find the maximum
that satisfies all the demands of the commodities is equivalent to find the maximum  flow in
flow in , since we assume the existence of
, since we assume the existence of , the maximum
, the maximum  flow in
flow in 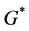 is with flow value
is with flow value  and we can use any maximum flow algorithm to obtain the maximum
and we can use any maximum flow algorithm to obtain the maximum 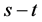 flow.
flow.
● For each commodity , the number of paths found is at most
, the number of paths found is at most  and so the size of
and so the size of 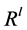 is largely smaller than
is largely smaller than . Since the existence of a feasible splittable flow
. Since the existence of a feasible splittable flow  satisfying all demands, at the end of step 2 we have that
satisfying all demands, at the end of step 2 we have that  and the total path value of
and the total path value of  is
is  for each
for each .
.
● The new algorithm applies the Round Robin strategy to find paths. In each round, each commodity finds at most one path in the current flow , this strategy guarantees some fairness in certain degree. To show the effectiveness of the Round Robin strategy, we compare our algorithm to the one that does not use the strategy in the next section. The computational results show that this strategy does have some advantages for this problem.
, this strategy guarantees some fairness in certain degree. To show the effectiveness of the Round Robin strategy, we compare our algorithm to the one that does not use the strategy in the next section. The computational results show that this strategy does have some advantages for this problem.
4. Computational Results
The testing instances are generated by the Transit Grid generator developed by G.Waissi [13] . The topology of those instances (see Table 1) looks close to the transportation networks and may be well-suited for the MPLS networks. In this paper, we propose some results for the multi-commodity case. Tests were performed on an Intel Core 2.4 GHz processor, 4 GB of RAM. We use CPLEX 12.5.1 to solve the arc-flow model. The running time of the CPLEX-solver is restricted to 50 seconds for each instance. The testing results are reported on Table 2 and Table3
In our testing, the total demands of the commodities in each instance are taken as the largest. While in practice, the demand of each commodity may be much less than the amount we take, hence the congestions we obtained may be larger than 1. For simplicity, we denote the algorithm in [1] by H1. In this section, we also compare our algorithm to the one that not using the Round Robin strategy. That is the one which find paths from  for each commodity until the total path values is its demand, and then go to the next commodity, denote the algorithm by H2. The new algorithm proposed in this paper is denoted by H3. In Table 2, for each instance name, the first column followed is the number of commodities, and then followed the number of paths each commodity can use, and the next four columns are the congestions obtained by H1, H2, H3 and the CPLEX-solver in 50 seconds, and the last three columns followed are the ratios between the congestions of each of the three heuristic algorithms and the CPLEX-solver for each instance. The empty positions in Table 2 and Table 3 are because of the size of the instance runs out of memory, and hence no results are given. In Table 3, the last four columns are the corresponding running times for each instance.
for each commodity until the total path values is its demand, and then go to the next commodity, denote the algorithm by H2. The new algorithm proposed in this paper is denoted by H3. In Table 2, for each instance name, the first column followed is the number of commodities, and then followed the number of paths each commodity can use, and the next four columns are the congestions obtained by H1, H2, H3 and the CPLEX-solver in 50 seconds, and the last three columns followed are the ratios between the congestions of each of the three heuristic algorithms and the CPLEX-solver for each instance. The empty positions in Table 2 and Table 3 are because of the size of the instance runs out of memory, and hence no results are given. In Table 3, the last four columns are the corresponding running times for each instance.
From Table 3, we can note that the time spent for H1, H2 and H3 has little differences, all of the three heuristic algorithms run faster than the CPLEX-solver, and when the size of the instance or the number of paths that a commodity can use increases, the time spent for the CPLEX-solver has a big fluctuation, and most of the instances cannot obtain the exact solutions in the given time, we list the congestions obtained by the CPLEXsolver in 50 seconds. From column 4 and column 6 in Table 2, we can see that in the 50 test instances, 64% of the congestion values obtained by H3 is less than H1, and 30% have the same congestion values, and H1 has only 6% of the 50 congestion values that is less than H3. From column 5 and column 6 in Table 2, we note that 34% of the congestion values obtained by H3 are less than H2, and only 16% of the congestion values obtained by H2 are less than H3, this shows that the Round Robin strategy is useful in the heuristic algorithm. From the last three columns of Table 2, we can note that for all the 40 sets of gaps, H1 has 24 instances that have gaps less than or equal to 1.5, while H3 has 31 instances with this property and H2 has 30. We can also note that H1 has 5 instances with gaps larger than 2 and H2 has 2 instances with this property, while H3 has no instance with gaps larger than 2. Hence we conclude that the performance of H3 outperforms H1 and H2. We know that increasing the size of path set for each commodity can minimize the congestion, but too large path set may also increasing the running time. So how to find paths for each commodity efficiently is a big challenge for this problem.
5. Conclusion
In this paper, we consider the problem of minimizing congestion in the MPLS networks. We propose a new heuristic algorithm. This algorithm is based on the strategy that reduces the whole feasible path set for each commodity, and a Round Robin strategy is also used. The computational results show that the new algorithm is

Table 1 . Sizes of testing instances. For each instance name, the first column followed is the number of vertices, and then the number of edges and finally the maximum capacity of the edges in the instance.

Table 2. The congestions obtained by the 3 testing heuristic algorithms and the CPLEX solver. The last three columns are the gaps between each of the 3 algorithms and the CPLEX-solver.

Table 3. Running times of the 3 test algorithms and the CPLEX solver.
much better than the algorithm that we proposed before. One main limitation of the new algorithm is that it needs to solve a mixed integer linear programming, when the number of commodities is sufficiently large, the running time of the algorithm may be large. However, the idea of the algorithm provides a good feasible direction for solving this problem. In the future, we will continue to do research on how to find better feasible path set for each commodity, not only this, we will design effective strategies to solve the mixed integer linear programming more quickly.
Acknowledgements
The work is supported by the National Natural Science Foundation of China under Grant No. 71171189, the key project of the National Natural Science Foundation under Grant No. 11331012 and the national key basic research development plan (973 Plan) project under Grant No. 2011CB706901.
NOTES
*Corresponding author.