Multi-Cultural Dynamics on Social Networks under External Random Perturbations ()
1. Introduction
Connectivity is the hallmark of the emerging world order. Competition and collaboration are central to stable order among conflicting interests of various groups, entities and nations. In his work [1] , Axelrod presents an excellent account of the complexity of cooperation. Motivated by this work, we systematically explore the behavior of a social network under cultural dynamic interactive forces in this paper. In our model, each individual member of a society is influenced by his/her interactions with fellow members of the family, neighborhood, region and the universe. There could also be a self-influence of reinforcement, or revision, and/or adaptation. The behavior of such complex and highly interacting social networks can be modeled by stochastic interconnected dynamical systems. Such a dynamic may be influenced both by deterministic and stochastic cultural forces. In this paper, we derive dynamic equations that incorporate intra-cultural and inter-cultural affinities subject to either the internal and/or the external random perturbations.
For the ease of exposition, we describe primarily the dynamics for single culture with multiple attributes, features/traits. However, our intrinsic framework is readily adaptable to multiple cultures, albeit with considerable algebraic complexity. Our primary focus here is on laying down an investigation of both qualitative and quantitative properties of these dynamical systems. For instance, our interests in pre-specified bounds, invariant sets, and stability properties are motivated by the evolution of coherent neighborhoods [2] , regions of conflicts, and the stability of emergent states. In the context of network sciences, in this work, we consider the dual dynamics of changing nodes (communities, entities, etc.) and also varying/evolving edges/connections (interactions, modalities, relations, etc.).
The organization of this paper is as follows: In Section 2, the basic deterministic and stochastic models of mono-cultural state structural and mono-cultural network dynamics are developed. We outline the problem formulation in Section 3. The sufficient conditions for the cohesion of mono-cultural community are presented in Section 4. In Section 5, we describe a nonlinear mono-cultural stochastic dynamic system and provide the sufficient conditions for the qualitative and quantitative properties stochastic network mono-cultural dynamic systems. Conclusions regarding the role and scope of our work are made in Section 6.
2. Basic Mono-Cultural Network Dynamics Models
We assume that the single-cultural system is under the influence of both personal intra and inter-member cultural forces. The cultural forces are induced by the magnitudes of current size of individual cultural state and the relative magnitudes of cultural states of the members in the home, neighborhood, and community. The influence of these cultural forces are measured by the degree (intensity/magnitude of desire to assimilate or changes) of self-cultural and inter-member cultural affinities.
Specifically, we consider m mono-cultural members living in a given community. The monoculture may have n features, where each feature describes a different aspect of the culture. Thus, we have n-dimensional cultural space. The cultural state of an individual member 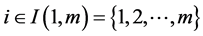 in the community at a time t is denoted by an n-dimensional vector
in the community at a time t is denoted by an n-dimensional vector . We assume that there is a synchronous dynamic with no time delays, that is, each individual member knows the instantaneous relative cultural affinity of all other individual members. For
. We assume that there is a synchronous dynamic with no time delays, that is, each individual member knows the instantaneous relative cultural affinity of all other individual members. For  each pair
each pair  of community members, the relative affinity of the i-th member relative to the j-th member is defined by
of community members, the relative affinity of the i-th member relative to the j-th member is defined by
 , (2.1)
, (2.1)
where
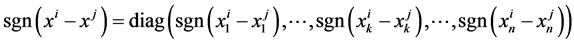
is an  diagonal matrix;
diagonal matrix;  is ‒1, 0, or 1 depending on whether
is ‒1, 0, or 1 depending on whether
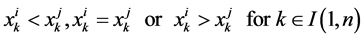
and
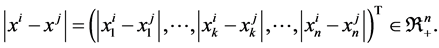
In the following, we develop a mono-cultural network dynamic model. The development of the model consists of two parts, namely, mono-cultural network model of state dynamics and structural (connectivity) dynamics. These models are described below.
2.1. Deterministic Mono-Cultural State Dynamic Model
The development of the mono-cultural state model is outlined as follows. For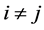 , let
, let  and
and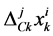 be the changes in the k-th component of the cultural state of the i-th member due to his/her own change, the change due to the direct influence of j-th member and the change due to the social influence of the community on its members over an interval of time
be the changes in the k-th component of the cultural state of the i-th member due to his/her own change, the change due to the direct influence of j-th member and the change due to the social influence of the community on its members over an interval of time  for
for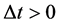 , respectively. The effects of the cultural forces on the change of k-th component of the cultural state of the i-th member relative to k-th components of both the personal and the j-th member per capita changes of the respective cultural affinities generated by the intrainter and community effects over the time interval of length,
, respectively. The effects of the cultural forces on the change of k-th component of the cultural state of the i-th member relative to k-th components of both the personal and the j-th member per capita changes of the respective cultural affinities generated by the intrainter and community effects over the time interval of length,  , are
, are
 (2.2)
(2.2)
 (2.3)
(2.3)
and
 (2.4)
(2.4)
respectively, where 


 for all
for all 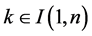
and all . The matrix
. The matrix  represents the strength or affinity efficiency, and it is referred to as an affinity matrix of k-th feature of the culture. Hence, the net effects due to the self-influence, the community-influence and the influence of the j-th member on the change of k-th component of the cultural state of i relative to the corresponding components of the i-th and the j-th member respective changes over the interval of time of length,
represents the strength or affinity efficiency, and it is referred to as an affinity matrix of k-th feature of the culture. Hence, the net effects due to the self-influence, the community-influence and the influence of the j-th member on the change of k-th component of the cultural state of i relative to the corresponding components of the i-th and the j-th member respective changes over the interval of time of length,  , is
, is
 . (2.5)
. (2.5)
From (2.5), the change of the cultural state of the i-th member relative to the cultural state of the j-th member over the time interval  for
for 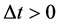 is
is
 (2.6)
(2.6)
where  and c are
and c are  matrices defined by:
matrices defined by:
 (2.7)
(2.7)
Thus for each pair , the total change of the cultural state of the i-th member relative to the cultural states of the members in the community over the interval of time
, the total change of the cultural state of the i-th member relative to the cultural states of the members in the community over the interval of time  for
for 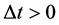 is
is
 (2.8)
(2.8)
For very small , (2.8) reduces to the following deterministic mathematical model of continuous time mono-cultural cultural state dynamic of social network:
, (2.8) reduces to the following deterministic mathematical model of continuous time mono-cultural cultural state dynamic of social network:
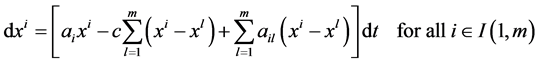 (2.9)
(2.9)
which can be written as:
 (2.10)
(2.10)
where f represents the relative affinity potential between any pair of the members of the dynamic cultural network defined on  into itself, and it is defined by:
into itself, and it is defined by:
 (2.11)
(2.11)
2.2. Deterministic Mono-Cultural Structural Dynamic Model
Using the developed mono-cultural state dynamic model, we construct a mono-cultural structural dynamic model as below. For this purpose, for given an i-th member in the community, we form pair with a j-th member as  and associate an n-dimensional cultural affinity link vector
and associate an n-dimensional cultural affinity link vector  at a time t. Now, by following the above argument, using (2.9) and algebraic simplifications, we have
at a time t. Now, by following the above argument, using (2.9) and algebraic simplifications, we have


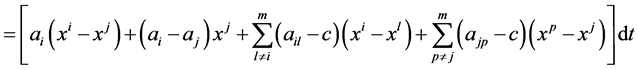
 (2.12)
(2.12)
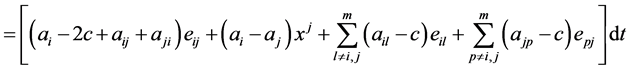
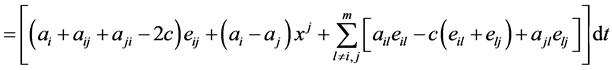

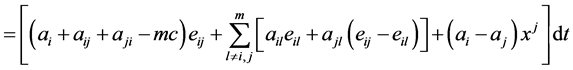
 (2.13)
(2.13)
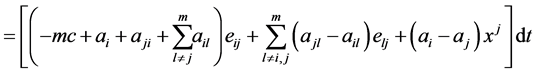 (2.14)
(2.14)
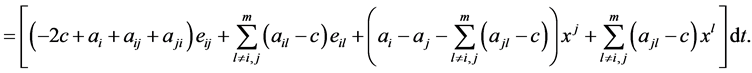 (2.15)
(2.15)
From the above description, we note that we have at least four equivalent mono-cultural structural dynamic models for the mono-cultural social network process. These models are presented below. Of course, these equivalent structural models provide a source of drawing different inferences.
2.3. Deterministic Mono-Cultural Network Dynamic Model
From (2.9), (2.12), (2.13), (2.14) and (2.15), a mono-cultural prototype network dynamic model is described by either one of the following at least four equivalent interconnected representations:
 (2.16)
(2.16)
 (2.17)
(2.17)
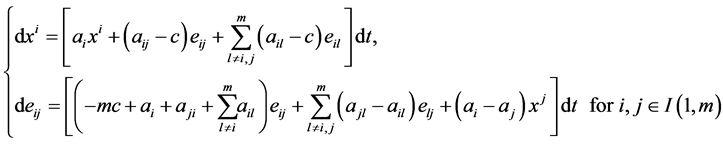 (2.18)
(2.18)
 (2.19)
(2.19)
2.4. Deterministic Transformed Mono-Cultural Network Dynamic Systems
In order to investigate the qualitative and quantitative properties of mono-cultural interconnected network dynamic systems, we transform the mono-cultural network dynamic systems developed in Subsection 2.3. For this purpose, we assume the following:

In appearance, this assumption seems to be restrictive, however it does allow to have different strengths of self-affinity as well as affinity efficiency yielding the uniform rate per unit size of cultural size of components of the cultural state vector .
.
Now, we define the following linear invertible transformation to reduce (2.16), (2.17), (2.18) and (2.19) into suitable forms. Let us define a linear transformation:
 (2.20)
(2.20)
where  is an
is an  diagonal matrix defined by
diagonal matrix defined by
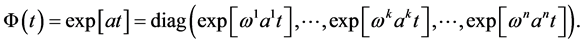
This transformation induces an affinity-link transformation as follows:
 (2.21)
(2.21)
Applying these transformations to systems of dynamic Equations (2.16), (2.17), (2.18) and (2.19), we obtain
 (2.22)
(2.22)
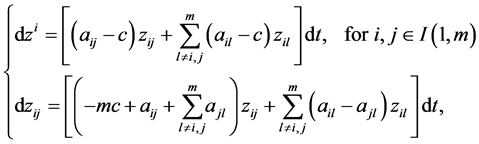 (2.23)
(2.23)
 (2.24)
(2.24)
 (2.25)
(2.25)
2.5. Center of Deterministic Mono-Cultural Network Dynamic Systems
In this subsection, we examine the weighted/scaled mono-cultural network dynamic system. This is achieved by finding the weighted or scaled center of transformed mono-cultural network dynamic systems. A weighted/ scaled center is of any one of the equivalent transformed systems in Subsection 2.4. Thus, under the following assumption on the coupling or interactions between any pair of members of the community:
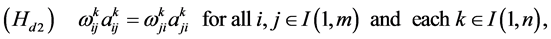
we define a center . We note that
. We note that
 (2.26)
(2.26)
From this observation, it is easy to verify that z is stationary center of the transformed interconnected monocultural network dynamic systems. To examine a center of the original interconnected mono-cultural network dynamic system, we apply the transformation defined in (2.20) to define a candidate for a center as:
 (2.27)
(2.27)
where  is as defined above. From hypotheses
is as defined above. From hypotheses  and
and , (2.9), (2.27), and the fact that z is the stationary solution of transformed system, we have
, (2.9), (2.27), and the fact that z is the stationary solution of transformed system, we have
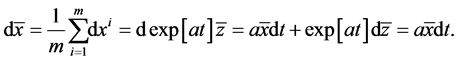
Thus the center of the original interconnected network dynamic system satisfies the following initial value problem:
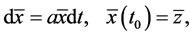 (2.28)
(2.28)
where  is stationary center of the transformed interconnected mono-cultural network dynamic systems. In fact, the center of the original interconnected network dynamic systems is time-varying stationary center. It signifies the time adjustment of the mono-cultural network dynamic center with the changes in the intra-intermember affinities of the community.
is stationary center of the transformed interconnected mono-cultural network dynamic systems. In fact, the center of the original interconnected network dynamic systems is time-varying stationary center. It signifies the time adjustment of the mono-cultural network dynamic center with the changes in the intra-intermember affinities of the community.
2.6. Stochastic Mono-Cultural Network Dynamic Model
We note that (A1) the size of individuals in a community is integral values, and (A2) the effects of affinity and/or in-affinity forces in community can cause a discrete time variation in parameters. In short, if the number of members in the system is large, the affinity/inter-affinity parametric  diagonal matrices
diagonal matrices  and c in (2.10) are subject torandom perturbations. Moreover, from (A1) and (A2), we assume that the random perturbations are described by stationary Gaussian process with independent increments. Hence:
and c in (2.10) are subject torandom perturbations. Moreover, from (A1) and (A2), we assume that the random perturbations are described by stationary Gaussian process with independent increments. Hence:
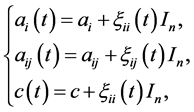 (2.29)
(2.29)
for  where
where  is an
is an  identity matrix;
identity matrix; ’s are Gaussian processes with independent increments that satisfy the following assumptions:
’s are Gaussian processes with independent increments that satisfy the following assumptions:
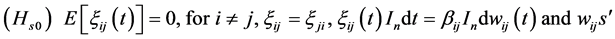 are normalized Wiener processes and
are normalized Wiener processes and 
 (2.30)
(2.30)
for  Therefore, by imitating the development of deterministic mono-cultural state (2.9) and any one of the structural models (2.12), (2.13), (2.14) and (2.15), one can arrive at the following equivalent monocultural prototype stochastic network dynamic models corresponding to equivalent deterministic models (2.16), (2.17),(2.18) and (2.19) [3] :
Therefore, by imitating the development of deterministic mono-cultural state (2.9) and any one of the structural models (2.12), (2.13), (2.14) and (2.15), one can arrive at the following equivalent monocultural prototype stochastic network dynamic models corresponding to equivalent deterministic models (2.16), (2.17),(2.18) and (2.19) [3] :
 (2.31)
(2.31)
 (2.32)
(2.32)
 (2.33)
(2.33)
 (2.34)
(2.34)
Moreover, in addition to assumption , we assume that the diffusion rate coefficients
, we assume that the diffusion rate coefficients  induced by a mono-cultural member self-affinity process satisfies the following assumption:
induced by a mono-cultural member self-affinity process satisfies the following assumption:

Moreover, we modify the linear transformation defined in (2.20) as:
 (2.35)
(2.35)
where  This transformation induces an affinity-link transformation as follows:
This transformation induces an affinity-link transformation as follows:
 (2.36)
(2.36)
Under these assumptions and using transformation, (2.35) and (2.36), mono-cultural inter connected network stochastic dynamic systems (2.31), (2.32), (2.33) and (2.34) reduce to:
 (2.37)
(2.37)
 (2.38)
(2.38)
 (2.39)
(2.39)
and
 (2.40)
(2.40)
Under assumption (Hs0), we have an assumption parallel to (Hd2) as:
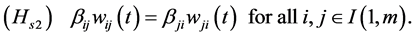
It is clear that the center of the transformed interconnected mono-cultural stochastic network dynamic systems is stationary. Thus, the center of the original interconnected stochastic network dynamic systems is stochastic process-varying stationary center.
Example 2.1 (Multi-agent-based mono-cultural Stochastic Network Dynamic System)
Multi-agent model [2] is extended to a cultural dynamic process. From Subsection 2.6 and using hypotheses (Hd1), (Hd2), (Hs0), (Hs1), (Hs2) and notations, a multi-agent-based mono-cultural Itô-Doob type stochastic network dynamic systems in the context of (2.32) is described by:
 (2.41)
(2.41)
where  and
and  are real-valued functions;
are real-valued functions;  and
and  are odd functions, and are defined by:
are odd functions, and are defined by:
 (2.42)
(2.42)
From assumptions (Hd1), (Hd2), (Hs0), (Hs1), (Hs2) and transformations (2.35) and (2.36), (2.41) reduces to:
 (2.43)
(2.43)
3. Problem Formulation
The stochastic network dynamic model and Example 2.1 motivate us to study the nonlinear mono-cultural stochastic network dynamical system. Let us consider a mono-cultural dynamic system consisting of m members in a community with n features of a single-cultural community described by the following large-scale system of stochastic differential equations:
 (3.1)
(3.1)
where ; the drift and diffusion pairs of functions
; the drift and diffusion pairs of functions  and
and  are considered to be as potential functions that govern the individual member self-affinity, mono-cultural community affinity and intermember affinities in the absence and the presence of random external perturbations. The
are considered to be as potential functions that govern the individual member self-affinity, mono-cultural community affinity and intermember affinities in the absence and the presence of random external perturbations. The  and
and  are assumed to be odd functions. Moreover, they possess both long-range attractions and the short-range repulsion properties. We make the following assumptions on (3.1) (H):
are assumed to be odd functions. Moreover, they possess both long-range attractions and the short-range repulsion properties. We make the following assumptions on (3.1) (H):
1)  is an n-dimensional random vector defined on a complete probability space
is an n-dimensional random vector defined on a complete probability space 
2)  is an increasing family of sub-s-algebra of F;
is an increasing family of sub-s-algebra of F;
3) 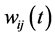 are as defined in (2.29);
are as defined in (2.29);
4)  are
are 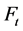 -measurable for all
-measurable for all ;
;
5)  and
and  are mutually independent foe each
are mutually independent foe each 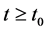 and
and ;
;
6)  and
and ;
;
7)  and functions
and functions  and
and  are odd; for each
are odd; for each 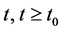 and each
and each
 k-th components of
k-th components of  and
and  are functions of the k-th component of
are functions of the k-th component of 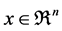 (nonlinear coordinate functions);
(nonlinear coordinate functions);
8) for each 
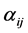 and
and  are
are  non-negative diagonal constant matrices defined in (2.30) and satisfy assumptions
non-negative diagonal constant matrices defined in (2.30) and satisfy assumptions  and
and ;
;
9)  and
and  are smooth enough functions to insure the existence of a solution process
are smooth enough functions to insure the existence of a solution process of (3.1).
of (3.1).
From assumption (H) 7), 8), and 9), and transformations (2.35) and (2.36), (3.1) reduces to:
 (3.2)
(3.2)
where 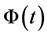 is a linear nonsingular transformation
is a linear nonsingular transformation

defined in (2.35) and (2.36); moreover, it is a fundamental solution process [3] of: , where
, where  and
and . We further note that the rate coefficients preserve all conditions outlined in assumption (H).
. We further note that the rate coefficients preserve all conditions outlined in assumption (H).
A weighted/scaled center can be defined under various assumptions on the coupling/interaction coefficients  and
and  in (3.1). For example:
in (3.1). For example:
Moving Isotropic and Reciprocal Cases 
In these cases, we define a center as , and we observe that the center is a time varying random process. This is because of the fact that
, and we observe that the center is a time varying random process. This is because of the fact that
 that is,
that is,
 . (3.3)
. (3.3)
In order to investigate the qualitative properties of the moving isotropic and reciprocal center x of monocultural network dynamic system (3.1), we need to rewrite (3.1) to reduce the moving center to the zero (trivial center). For this purpose, we set  and note
and note  Using this, (3.1) reduces to:
Using this, (3.1) reduces to:
 (3.4)
(3.4)
Historically, the Lyapunov Second Method/Energy Method has played a significant role in analyzing qualitative and quantitative properties of nominal state of dynamic systems in biological, chemical, engineering, physical and social sciences [2] -[4] . We extend these techniques to investigate properties of nonlinear mono-cultural network dynamic systems under environmental and random structural perturbations. In particular, we investigate properties such as cohesion, convergence, and stability of solution process of system (3.1). The collective behavior of such systems is explored in relation to its weighted/scaled center(s) [2] [5] [6] . Insights provided by these qualitative and quantitative estimates of the interaction patterns of collective behavior of nonlinear mono-cultural stochastic network dynamics under various formulations of social potentials (attraction/repulsion) can be very useful in practice.
It is easy to see through a special example below that the type of role of the random external perturbations play in collective behavior of mono-cultural community members in relation to the centers. Specifically, we note that if the individual member community is culturally further away from all other members, the random perturbations can cause it to move the member towards the weighted center. If it is close to all other members, then random fluctuations cause to move the member away from the center.
4. Cohesion of Mono-Cultural Community
To illustrate the utility of a Lyapunov-like energy method for establishing cohesion property of mono-cultural community under random perturbations, in this section, we consider a special case of system (3.1) in the context of (2.42) for maintaining the essential character of the dynamics. We consider Example 2.1with 
 and the rate coefficients in (3.1) are:
and the rate coefficients in (3.1) are:
 (4.1)
(4.1)
By setting  and
and  noting
noting 


 and
and  (3.2) reduces to:
(3.2) reduces to:
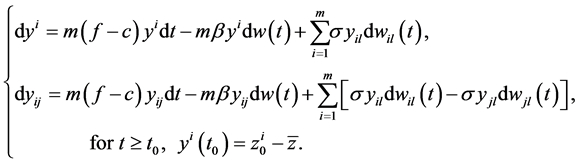 (4.2)
(4.2)
In order to investigate the qualitative properties of the center of mono-cultural network dynamic systems under random environmental perturbations, we consider a candidate for a Lyapunov/Energy function as:
 (4.3)
(4.3)
for the i-th member of the mono-cultural community evolving under random environmental perturbations, where . By applying the Itô–Doob differential formula [3] [4] [7] along the stochastic vector field (4.2), we have
. By applying the Itô–Doob differential formula [3] [4] [7] along the stochastic vector field (4.2), we have
 , (4.4)
, (4.4)
where  is the smallest eigen value of the matrix:
is the smallest eigen value of the matrix:
 (4.5)
(4.5)
Under the condition on matrix P in (4.5), an estimate on L in (4.4) and the application of comparison theorem [3] [4] , we conclude that the trivial solution of (4.2) is asymptotically stable in the mean-square. Thus, the random process varying center of (2.41) is asymptotically stable in the mean-square.
Remark 4.1
In the absence of the random fluctuations, the condition in (4.5) also assures that the mono-cultural network dynamic system (2.34) is asymptotically stable.
5. Nonlinear Mono-Cultural Network Stochastic Dynamic Systems
We now turn to the more general nonlinear mono-cultural network dynamic system described by (3.1). Furthermore, we assume that the potential functions are either isotropic-reciprocal or anisotropic. Under assumption (H), setting  and the assumption of x being the moving isotropic, reciprocity, (4.1) is reduced to (4.4).
and the assumption of x being the moving isotropic, reciprocity, (4.1) is reduced to (4.4).
In fact, by recalling 
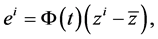
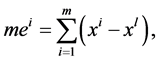
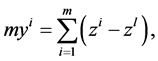
 and
and  the transformed system (3.2) in the context of (3.4) is as follows:
the transformed system (3.2) in the context of (3.4) is as follows:
 (5.1)
(5.1)
for 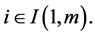
Let  be a space of k-dimensional continuous vector functions
be a space of k-dimensional continuous vector functions  and
and  defined on
defined on  into
into  that possesses continuous partial derivatives
that possesses continuous partial derivatives  and
and  on
on  for
for
 . For each fixed i, and any
. For each fixed i, and any 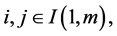 a linear operator L defined on
a linear operator L defined on  into
into  as follows [3] [4] :
as follows [3] [4] :
 (5.2)
(5.2)
where the function  is the sum of functions
is the sum of functions  and
and ;
;  and
and  are defined as:
are defined as:
 (5.3)
(5.3)
and
 (5.4)
(5.4)
where
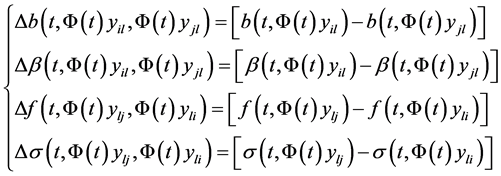 (5.5)
(5.5)
Let CK and VK denote the classes of functions that belong to  where CK and VK are increasing concave and convex functions on
where CK and VK are increasing concave and convex functions on , respectively; moreover,
, respectively; moreover,  for
for  CK and
CK and , respectively. In the following, we are ready to present very general sufficient conditions concerning the qualitative properties of mono-cultural network dynamic system under external random perturbations (5.1).
, respectively. In the following, we are ready to present very general sufficient conditions concerning the qualitative properties of mono-cultural network dynamic system under external random perturbations (5.1).
Theorem 5.1. Assume that the mono-cultural dynamic system (5.1), its energy like function V and corresponding linear differential operator L in (5.2) satisfy the following system inequalities for each fixed i, j and :
:
(a)  (5.6)
(5.6)
where  for each
for each 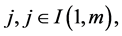
 ;
;
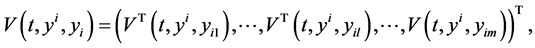
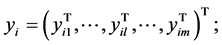
(b)  (5.7)
(5.7)
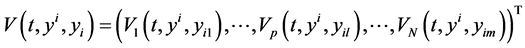

(c)  is maximal solution of the following system block comparison system of differential equations [8] :
is maximal solution of the following system block comparison system of differential equations [8] :
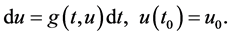 (5.8)
(5.8)
Then qualitative properties of the block trivial solution of a block comparison dynamic system described by (5.8) imply that the qualitative properties of mono-cultural center of the transformed dynamic system in the quadratic mean.
Proof. Using the hypotheses of theorem and the application of block comparison theorems [8] , we obtain the following estimate:
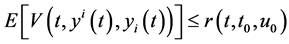 (5.9)
(5.9)
provided that
 (5.10)
(5.10)
Finally, under the conditions of the theorem and following the standard argument [2] [4] [9] , the proof of the theorem follows from the estimate (5.9).
Example 5.1. For positive numbers , functions
, functions  and
and  are admissible in Theorem 5.1.
are admissible in Theorem 5.1.
6. Conclusion
In this paper, we have investigated a broad class of social network dynamic behaviors focusing on a mono-cultural societal/community member interacting network dynamic systems. Our principal interests are in the qualitative and quantitative properties such as robustness, convergence and stability. Utilizing energy-like functions and the theory of differential inequalities, we derive explicit conditions that are sufficient, algebraically simple and computable. Our method does not require the explicit knowledge of solution processes. The qualitative results such as convergence and stability are readily applicable to a broad class of social networks. We intend to pursue these goals in a future paper.
Acknowledgements
This research was supported by the Mathematical Sciences Division, US Army Research Office; the first author by Grant No. W911NF-05-10209, and the second author by Grant No. W911NF-12-1-0090.