A Note on the Height of Transitive Depth-One Graded Lie Algebras Generated by Their Local Parts ()
Let the characteristic  of the base field be greater than two. In [1] , V.G. Kac defined the local part of a graded Lie algebra
of the base field be greater than two. In [1] , V.G. Kac defined the local part of a graded Lie algebra 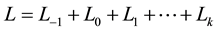 to be
to be 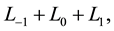 which we will assume to be finite dimen- sional. We will refer to
which we will assume to be finite dimen- sional. We will refer to 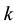 as the height of
as the height of .
.
Lemma 1. If 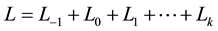 is a transitive graded Lie algebra which is generated by its finite- dimensional local part, then the height
is a transitive graded Lie algebra which is generated by its finite- dimensional local part, then the height  of
of  is less than or equal to
is less than or equal to , where
, where 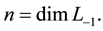
Proof. If 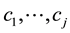 are any elements of
are any elements of  (or
(or 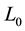 or
or , respectively) and
, respectively) and  is an element of
is an element of  then we have by the Leibniz rule that
then we have by the Leibniz rule that
![]()
Now, ![]() is an element of
is an element of![]() , (or
, (or ![]() or
or![]() , respectively) which is zero, since
, respectively) which is zero, since ![]() is assumed to be greater than two, and the depth of
is assumed to be greater than two, and the depth of ![]() is one. Because of the commutativity of
is one. Because of the commutativity of![]() , we have that
, we have that![]() . Consequently, by the transitivity of
. Consequently, by the transitivity of![]() , we have
, we have ![]() for
for ![]() greater than or equal to
greater than or equal to![]() .
. ![]()
Note that the height of the Jacobson-Witt algebra ![]() is
is![]() .
.
Because the gradation spaces of positive degree of transitive graded Lie algebras are contained in Cartan prolongations, those gradation spaces will be finite dimensional whenever the local part of the transitive Lie algebra is finite dimensional. Thus, when the gradation degrees of a transitive graded Lie algebra with a finite- dimensional local part are bounded, the Lie algebra is itself finite dimensional.