An Algebraic Proof of the Existence of a Competitive Equilibrium in Exchange Economies ()
1. Introduction
The standard excess demand argument for existence of competitive equilibriain exchange economies invokes maximizing the value of the excess demand of the economy (the aggregate excess demand) and thereby adjusting the prices toward equilibrium [1] -[3] . At least for pedagogical purpose, one may legitimately interpret the adjustment procedure, often referred to as tatonnement, as that in which a price-setting agency, the so-called Walrasian auctioneer, gathers the information as regards to each agent’s excess demand and then fine-tunes the prices so as to raise the prices of the commodities that are over-demanded (with a positive aggregate excess demand registered) and to lower the prices of the commodities that are under-demanded (with a negative aggregate excess demand registered). It is true that the excess demand function is a very useful device that renders the fixed point theory nicely applicable to the proof of the existence of a market-clear price vector. Such a technical device, powerful though as it is in remarkably simplifying the formulation, nonetheless suggests a centralized coordination mechanism. Exploiting the Perron-Frobenius theorem on stochastic matrices, a well known result in linear algebra, we provide an alternative proof of the existence of a competitive equilibrium without resorting to such an artificial price-setting mechanism. It is worth pointing out that in so doing our argument does not invoke aggregating the individuals’ excess demand, let alone to maximizing the market value of the aggregate excess demand. To the extent that the price-setting agency, as is embodied by the Walrasian auctioneer, personifies the coordination of the decentralized price system, “the invisible hand”, and hence rendering it more or less visible, our approach appears to be conceptually more natural. But a cost of awkwardness in algebraic manipulation has to be paid in our undertaking, compared to the rather neat formulation based on the Walrasian tatonnement. However, such a cost may be well justifiable for an economically appealing argument about the important idea of the invisible hand.
2. The Proof
We first restate the classical result on the existence of a competitive equilibrium.
Theorem. For any pure exchange economy with n commodities and m agents, in which each agent  has a preference represented by a utility function
has a preference represented by a utility function  that is continuous, concave and strongly monotone and an endowment
that is continuous, concave and strongly monotone and an endowment  such that the endowment of any commodity for the economy as a whole is positive, i.e.,
such that the endowment of any commodity for the economy as a whole is positive, i.e.,  there exists a competitive equilibrium.
there exists a competitive equilibrium.
Proof. First of all, normalize the endowment of each commodity of the community as one, i.e., 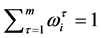 ,
, 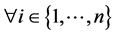 1. Consider the price simplex
1. Consider the price simplex . For any interior point
. For any interior point , let
, let . Notice that for any
. Notice that for any
 its i-th component is the percentage share of agent
its i-th component is the percentage share of agent ’s wealth spent on commodity i. Monotone preference implies
’s wealth spent on commodity i. Monotone preference implies . Convexity of preferences implies that for any agent
. Convexity of preferences implies that for any agent ,
, 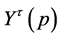 is convex at any interior point of
is convex at any interior point of . Also note that
. Also note that 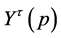 is upper-semi-continuous by Berge’s maximum theorem. For any
is upper-semi-continuous by Berge’s maximum theorem. For any , let
, let  be the convex hull of the limit points of any possible
be the convex hull of the limit points of any possible  where the sequence of interior points
where the sequence of interior points  approaches
approaches  That is,
That is, 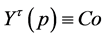 {
{ and
and  such that
such that 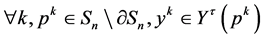 and that
and that 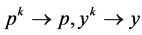 as
as  }. By definition,
}. By definition,  is upper-semi-continuous and convex-valued at any
is upper-semi-continuous and convex-valued at any  2.
2.
Let 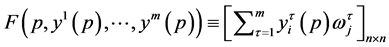 The sum of each column of F equals
The sum of each column of F equals
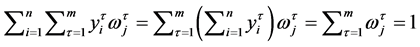 , hence F is a column stochastic matrix. Consequently, the Perron-Frobenius eigenvalue of F is one and there exists at least one corresponding eigenvector
, hence F is a column stochastic matrix. Consequently, the Perron-Frobenius eigenvalue of F is one and there exists at least one corresponding eigenvector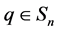 , i.e., Fq = q [4] .
, i.e., Fq = q [4] .
Consider any sequences  such that there exist
such that there exist 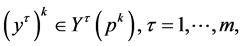 satisfying
satisfying
 for any k where
for any k where 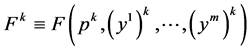 and that
and that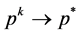 ,
, 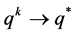 as
as  WLOG, assume
WLOG, assume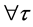 ,
,  As is established in the above,
As is established in the above,  is upper-semi-continuous. Hence,
is upper-semi-continuous. Hence,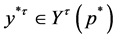 . Take the limit on both sides of
. Take the limit on both sides of  as
as 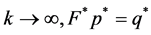 where
where
 The correspondence from p to q is closed.
The correspondence from p to q is closed.
We now prove that , {q(p)} is convex. Consider any two elements in {q(p)} say
, {q(p)} is convex. Consider any two elements in {q(p)} say  and
and  i.e., there exist
i.e., there exist ,
,  such that
such that 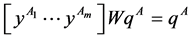 and
and 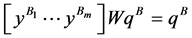 where
where  For any
For any  , we claim that there exist
, we claim that there exist ,
,  such that
such that
 (1)
(1)
Note the term in the brackets of LHS of Equation (1) equals
 (2)
(2)
Also notice that the RHS of Equation (1) equals

Substituting the above and (2) into (1) yields,

Since  and
and ,
,  there apparently exists
there apparently exists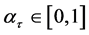 ,
, 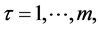 such that
such that
 , i.e., (1) holds. That is, for any
, i.e., (1) holds. That is, for any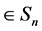 , {q(p)} is a convex set.
, {q(p)} is a convex set.
By Kakutani’s theorem, there exists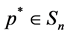 , such that
, such that  where
where . We now show that
. We now show that . For otherwise, then by the definition of
. For otherwise, then by the definition of  on
on , one possibility is that there exist sequences
, one possibility is that there exist sequences  such that
such that
 and that
and that ,
,  as
as  that is,
that is,  WLOG, assume
WLOG, assume  but some other components of
but some other components of  are zeros. Then we obtain from
are zeros. Then we obtain from 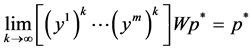 that
that  for any
for any  such that
such that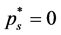 .
.
Thus for an agent τ endowed with a positive amount of commodity 1 (existence of such agent is guaranteed by the assumption that )
)  for anys such that
for anys such that , an impossibility in light of the strongly monotone preferences. In the case that
, an impossibility in light of the strongly monotone preferences. In the case that  itself is not a limit point for any sequence of interior price vectors that approaches
itself is not a limit point for any sequence of interior price vectors that approaches , but a convex combination of two such limit points, the above application applies to each of these two limit points. Thus,
, but a convex combination of two such limit points, the above application applies to each of these two limit points. Thus, 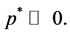 By simple algebraic manipulation one obtains from
By simple algebraic manipulation one obtains from
 that
that  i.e., all markets clear.
i.e., all markets clear.
NOTES
1One may do so by considering 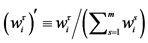 for any agent
for any agent  and commodity 𝑖and the prices adjusted to the accordingly changed units used to measure each commodity.
and commodity 𝑖and the prices adjusted to the accordingly changed units used to measure each commodity.
2A careful reader might be concerned with the closedness of the correspondence graph along . But it is not a problem. Consider any
. But it is not a problem. Consider any  and
and  such that
such that  and
and  as
as . One needs to come to grips with two scenarios. First of all suppose that for any
. One needs to come to grips with two scenarios. First of all suppose that for any ,
,  is a limit when some sequence of strictly positive price vectors approaches
is a limit when some sequence of strictly positive price vectors approaches . By the definition of
. By the definition of  on
on , for any k there exists
, for any k there exists 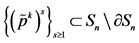 and
and ,
,  such that
such that ,
, 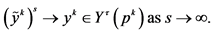 One can thus appropriately construct a sequence
One can thus appropriately construct a sequence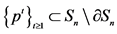 , with
, with  which converges to p and to which a sequence of
which converges to p and to which a sequence of , converging to
, converging to , is associated. Similar argument yet with more awkward notations applies to another scenario in which for some or all
, is associated. Similar argument yet with more awkward notations applies to another scenario in which for some or all ,
, 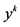 is not a limit point but a convex combinations of two vectors each of which is a limit point when one sequence of strictly positive price vectors approaches
is not a limit point but a convex combinations of two vectors each of which is a limit point when one sequence of strictly positive price vectors approaches 