On the Structure of Infinitesimal Automorphisms of the Poisson-Lie Group SU(2,R) ()
1. Introduction
Let 
be a Lie group. A Poisson-Lie structure on 
is a Poisson structure on 
for which the group multiplication is a Poisson map. Then as is usual in [1] -[3] , this is equal to giving an antisymmetric contravariant 2-tensor 
on 
which satisfies Jacobi identity and the relation
(1)
where 
and 
respectively denote the left and right translations in 
by 
and
. We note that a Poisson-Lie structure 
has rank zero at a neutral element 
of
, i.e.,
.
If we choose local coordinates 
in a neighborhood 
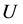of neutral element 
of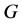
, the Poisson-Lie structure 
reads
(2)
where 
are smooth functions vanishing at 
and
(3)
where 
is the Poisson bracket associated to
. By this Poisson bracket, 
becomes a Lie algebra.
Let 
be a Lie algebra of
. The derivative of 
at 
defines a skewsymetric co-commutator map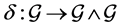 
such that:
1) The map 
is a 1-cocycle, i.e.,
(4)
2) The dual map 
is a Lie bracket on
.
The map 
is said a Lie bialgebra structure associated to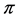
. Conversely, if 
is simply connected, any Lie bialgebra structure 
on the Lie algebra 
can be integrated to define a unique Poisson-Lie structure 
on 
such that
.
The bialgebra structure 
is called a coboundary one when there exists an skewsymmetric element 
of 
(the classical r-matrix) such that
(5)
Both properties 1) and 2) imply that the element 
has to be a constant solution of the modified classical Yang-Baxter equation (mCYBE) [4] -[6] :
(6)
Therefore, a constant solution of mCYBE 
on a given Lie algebra 
provide a coboundary Poisson-Lie structure 
on (connected and simply connected) group 
given by
(7)
where 
and 
denote respectively the left and right translations in 
by
.
Finally, recall that for semisimple Lie algebras, all Lie bialgebra structures are coboundaries, and the corresponding Poisson-Lie structures can be fully solved through the classical r-matrices.
In this work, We shall treat the case of the Poisson-Lie group
. We will calculate, firstly, all Poisson-Lie structures through the correspondence with Lie bialgebra; secondly, we will show that these Poisson-Lie structures are linearizable in a neighborhood of the unity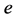 
of the group 
and, finally, we shall study infinitesimal automorphism of 
with a linear Poisson-Lie structure, and show that the Lie algebra
, consisting of all infinitesimal automorphisms is strictly contained in the Lie algebra 
consisting of Hamiltonian vector fields.
2. The Group 
and Lie Algebra 
The special unitary group 
is defined by
Let 
and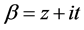
. 
can be identified with the unit sphere 
in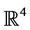 
with the unity
.
The Lie algebra 
of group 
is defined by
Let
a basis of
. The Lie bracket on 
is defined by
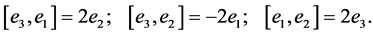
Through a straightforward computation, the left invariant fields associated to this basis had this local expression
3. The Lie Bialgebra Structure on 
and the Poisson Lie Structure on 
3.1. Lie Bialgebra Structures on 
Recall that the Lie algebra 
is semisimple. Then, all Lie bialgebra structures on 
are coboundaries, there exists an skew symmetric element r of 
such that the cocommutator 
is given by
We stress that the element 
satisfies the classical Yang-Baxter Equation (CYBE) (6). Through a long but straightforward computation, we show that these solutions are of the form
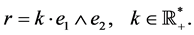(8)
So any Lie bialgebra structure of 
can be written as
(9)
3.2. Poisson-Lie Structures on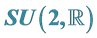 
Since the Lie bialgebra structures 
on 
are coboundaries, the Poisson-Lie structures on 
corresponding to 
are given by
where 
is the solution of Yang-Baxter equation given by (8) and 
and 
respectively denote the right and left translations in 
by
. Then, using
, 
and 
one gets
(10)
Let
(11)
be the components of 
in the basis 
of the bivector field.
4. Linearization of Poisson-Lie Structures on 
By taking back the formula (2), The Taylor series of the function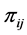s 
reads
(12)
where 
are the structure constants of a Lie algebra
, dual of a Lie algebra
, and the 
are smooth functions vanishing at
.
The term 
of (12) definines a linear Poisson structure, called the linear part of
. The linearization problem for a structure 
around 
is the following [7] [8] :
Linearization problem. Are there new coordinates where the functions 
vanish identically, so that the Poisson structure is linear in these coordinates?
Let us notice that the Lie bialgebra structure 
associated to 
defines a linear Poisson-Lie structure on the additive group 
that can be expressed as follows
(13)
where 
is the canonical basis of
.
Let us notice that (13) coincides with the linear part of
, so, the linearization problem would be the following:
There is a local Poisson diffeomorphism 
of a neighborhood in 
of G to a neighborhood of 0 in
?
If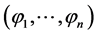 
are the components of
, then 
is solution of the system of equations
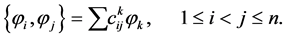(14)
For the Poisson-Lie structure on 
given by (10), the system of equations (14) would be
(15)
With the identification of the subgroups of the singular points and the symplectic leaves of 
and
, we have:
Proposition 1. The map
: 
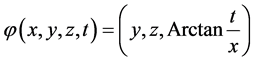is a diffeomorphism in the neighborhood of 
such that 
and
So, the Poisson-Lie structure 
on 
is linear in the new variables
(16)
and will be written
(17)
The Poisson bracket associated to 
reads
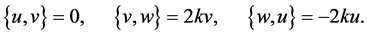(18)
5. Casimir Functions and Infinitesimal Automorphisms on 
Recall that for
, 
defines a derivation of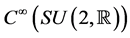
. Hence there corresponds a vector field
, which we call the Hamiltonian vector field. We denote by 
the Lie algebra of Hamiltonian vector fields.
A Casimir function on 
is a function 
such that 
for all function
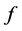. On the other words, 
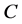is an element of the center of the Lie algebra
. By simple consideration, we know that for each Casimir function 
there exists a function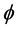 
of one variable such that
.
Each symplectic leaf is the common level manifold of casimir functions. So, these have for equation:
and hence are spheres.
By an automorphism of
, we mean a smooth vector field 
on 
such that
(19)
where 
denotes the Lie derivative along
.
If we denote by 
the Lie algebra consisting of all infinitesimal automorphism, it is easy to see that 
is an ideal of
. Let 
be a vector field of
. Then three function 
and 
must satisfy:
(20)
Now we shall clarify the gap between 
and
.
We consider the vector field
(21)
where 
are the components of the structure 
in the basis 
given by (11).
In the local coordinates 
given by (14), this vector field reads
(22)
A simple check shows that the components of 
satisfy the relations (20). So, the vector field 
belongs to
. In other hand, 
is locally Hamiltonian if and only if there exist a smooth function 
in a neighborhood of the unity 
of the group 
such that
, this is translated by the fact that 
is a solution of the following system of equations
(23)
It is easy to see that (23) does not admit solutions. Hence 
does not belong
. Thus we have proved:
Proposition 2. The ideal 
is strictly contained in the Lie algebra
.
In terms of Poisson cohomology [9] , recall that the first Poisson cohomology group 
is the quotient of the Lie algebra 
by its ideal
. Then, by Proposition 2, we show that the vector field 
defines a non trivial class
. On the other hand, this result shows that the classical result due to Conn [10] [11] stating that for a Poisson structure formally linearizable around a singular point any local Poisson automorphism is Hamiltonian, and not just in the 
category.