Common Fixed Point Theorems for Totally Quasi-G-Asymptotically Nonexpansive Semigroups with the Generalized f-Projection ()
Keywords:Totally Quasi-G-Asymptotically Nonexpansive Semigroup; Generalized f-Projection Operator; Modified Halpern Type Hybrid Iterative Algorithm; Strong Convergence Theorem
1. Introduction
In this paper, we denote by  and
and  the set of real number and the set of nature number respectively. Let
the set of real number and the set of nature number respectively. Let  be a real Banach space with its dual
be a real Banach space with its dual  and
and  be a nonempty, closed and convex subset of
be a nonempty, closed and convex subset of . The mapping
. The mapping  is the normalized duality mapping, defined by
is the normalized duality mapping, defined by

Recall that a mapping 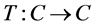 is said to be
is said to be  [1,2], if for each
[1,2], if for each ,
,
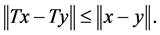
A mapping  is said to be
is said to be 
 , if there exists nonnegative real sequences
, if there exists nonnegative real sequences 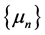 and
and  with
with  as
as  and a strictly increasing continuous function
and a strictly increasing continuous function
 with
with , such that for each
, such that for each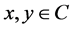 ,
,

We use  to denote the Lyapunov function defined by
to denote the Lyapunov function defined by

Obviously, we have

Recently, Chang et al. [3-5] and Li [6] introduced the uniformly totally quasi- -asymptotically nonexpansive mappings and studied the strong convergence of some iterative methods for the mappings in Banach space.
-asymptotically nonexpansive mappings and studied the strong convergence of some iterative methods for the mappings in Banach space.
Definition 1.1 [1] A countable family of mapping 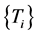 is said to be uniformly totally quasi-
is said to be uniformly totally quasi- -asymptotically nonexpansive, if
-asymptotically nonexpansive, if , and there exist nonnegative sequences
, and there exist nonnegative sequences ,
,  with
with 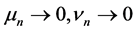
(as ) and a strictly increasing continuous function
) and a strictly increasing continuous function  with
with , such that for each
, such that for each
 , and each
, and each ,,
,,
 (1)
(1)
More recently, Wang et al. [7] studied the strong convergence for a countable family of total quasi- - asymptotically nonexpansive mappings by using the hybrid algorithm in 2-uniformly convex and uniformly smooth real Banach spaces. Quan et al. [8] introduced total quasi-
- asymptotically nonexpansive mappings by using the hybrid algorithm in 2-uniformly convex and uniformly smooth real Banach spaces. Quan et al. [8] introduced total quasi- -asymptotically nonexpansive semigroup containing many kinds of generalized nonexpansive mappings as its special cases and used the modified Halpern-Mann iteration algorithm to prove strong convergence theorems in Banach spaces.
-asymptotically nonexpansive semigroup containing many kinds of generalized nonexpansive mappings as its special cases and used the modified Halpern-Mann iteration algorithm to prove strong convergence theorems in Banach spaces.
We use  to denote the common fixed point set of the semigroup
to denote the common fixed point set of the semigroup , i.e.
, i.e. .
.
Definition 1.2 [8] One-parameter family  is said to be a quasi-
is said to be a quasi- -asymptotically nonexpansive semigroup, if
-asymptotically nonexpansive semigroup, if  and the following conditions are satisfied:
and the following conditions are satisfied:
(a)  for each
for each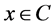 ;
;
(b) For each ,
,  ,
, ;
;
(c) For each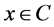 , the mapping
, the mapping  is continuous;
is continuous;
(d) For each ,
, 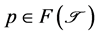 , there exists a sequences
, there exists a sequences  with
with  as
as , such that
, such that
 (2)
(2)
One-parameter family  is said to be a totally quasi-
is said to be a totally quasi- -asymptotically nonexpansive semigroup, if
-asymptotically nonexpansive semigroup, if , the conditions (a)-(c) and the following condition are satisfied:
, the conditions (a)-(c) and the following condition are satisfied:
(e) If , there exist sequences
, there exist sequences ,
, 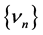 with
with  as
as  and a strictly increasing continuous function
and a strictly increasing continuous function  with
with , such that
, such that
 (3)
(3)
for all ,
, .
.
On the other hand, Wu et al. [9] introduced the generalized f-projection which extends the generalized projection and always exists in a real reflexive Banach space. Li et al. [10] proved some properties of the generalized f-projection operator and studied the strong convergence theorems for the relatively nonexpansive mappings.
In 2013, by using the generalized f-projection operator, Seawan et al. [11] introduced the modified Mann type hybrid projection algorithm for a countable family of totally quasi- -asymptotically nonexpansive mappings in a uniformly smooth and strictly convex Banach space with Kadec-Klee property.
-asymptotically nonexpansive mappings in a uniformly smooth and strictly convex Banach space with Kadec-Klee property.
Motivated by the above researches, in this paper, we introduce a new class of the totally quasi-G-asymptotically nonexpansive mappings which contains the class of the totally quasi- -asymptotically nonexpansive mappings and we extend from a countable family of mappings to the totally quasi-G-asymptotically nonexpansive semigroup. Then we modify the Halpern type hybrid projection algorithm by using the generalized f-projection operator for uniformly total quasi-G-asymptotically nonexpansive semigroup and prove some strong convergence theorems under some suitable conditions. The results presented in this paper extend and improve some corresponding ones by many others, such as [1,2,7,8,10,11].
-asymptotically nonexpansive mappings and we extend from a countable family of mappings to the totally quasi-G-asymptotically nonexpansive semigroup. Then we modify the Halpern type hybrid projection algorithm by using the generalized f-projection operator for uniformly total quasi-G-asymptotically nonexpansive semigroup and prove some strong convergence theorems under some suitable conditions. The results presented in this paper extend and improve some corresponding ones by many others, such as [1,2,7,8,10,11].
2. Preliminaries
This section contains some definitions and lemmas which will be used in the proofs of our main results in the next section.
Throughout this paper, we assume that  be a real Banach space with its dual space
be a real Banach space with its dual space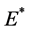 . A Banach space
. A Banach space
 is said to be strictly convex, if
is said to be strictly convex, if 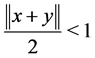 for all
for all  with
with  and
and .
.  is said to be uniformly convex, if
is said to be uniformly convex, if  for any two sequences
for any two sequences ,
,  in
in  with
with  and
and . A Banach space
. A Banach space  is said to be smooth, if
is said to be smooth, if  exists for each
exists for each
 with
with .
.  is said to be uniformly smooth, if the limit is attainted uniformly for each
is said to be uniformly smooth, if the limit is attainted uniformly for each .
.
It is well known that the normalized dual mapping  holds the properties:
holds the properties:
(1) If  is a smooth Banach space, then
is a smooth Banach space, then  is single-valued and semi-continuous;
is single-valued and semi-continuous;
(2) If  is uniformly smooth Banach space, then
is uniformly smooth Banach space, then  is uniformly norm-to-norm continuous operator on each bounded subset of
is uniformly norm-to-norm continuous operator on each bounded subset of .
.
A Banach space  is said to have Kadec-Klee property, if for any sequence
is said to have Kadec-Klee property, if for any sequence  satisfies
satisfies  and
and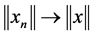 , then
, then . As we all know, if
. As we all know, if  is uniformly convex, then
is uniformly convex, then  has the Kadec-Klee property.
has the Kadec-Klee property.
Now, we give a functional , defined by
, defined by
 (4)
(4)
where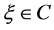 ,
,  ,
,  is a positive real number and
is a positive real number and  is proper, convex and lower semi-continuous. From the definition of
is proper, convex and lower semi-continuous. From the definition of  and
and , it is easy to see the following properties:
, it is easy to see the following properties:
(1)  is convex and continuous with respect to
is convex and continuous with respect to  when
when  is fixed;
is fixed;
(2)  is convex and lower semi-continuous with respect to
is convex and lower semi-continuous with respect to  when
when  is fixed.
is fixed.
Definition 2.1 [9]  is said to be a generalized f-projection operator, if for any
is said to be a generalized f-projection operator, if for any ,
,
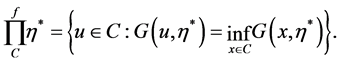 (5)
(5)
Lemma 2.2 [9] Let  be a real reflexive Banach space with its dual
be a real reflexive Banach space with its dual ,
,  be a nonempty closed and convex subset of
be a nonempty closed and convex subset of . Then
. Then  is a nonempty closed and convex subset of
is a nonempty closed and convex subset of  for all
for all . Moreoverif
. Moreoverif  is strictly convex, then
is strictly convex, then  is a single-valued mapping.
is a single-valued mapping.
Recall that if  is a smooth Banach space, then the normalized dual mapping
is a smooth Banach space, then the normalized dual mapping  is single-valued, i.e. there exists unique
is single-valued, i.e. there exists unique  such that
such that 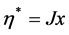 for each
for each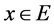 . Then (4) is equivalent to
. Then (4) is equivalent to
 (6)
(6)
And in a smooth Banach space, the definition of the generalized f-projection operator transforms into:
Definition 2.3 [10] Let  be a real smooth Banach space and
be a real smooth Banach space and  be a nonempty, closed and convex subset of
be a nonempty, closed and convex subset of . The mapping
. The mapping  is called generalized f-projection operator, if for all
is called generalized f-projection operator, if for all ,
,
 (7)
(7)
Now, we give the definition of the totally quasi- -asymptotically nonexpansive mapping and the totally quasi-
-asymptotically nonexpansive mapping and the totally quasi- -asymptotically nonexpansive semigroup.
-asymptotically nonexpansive semigroup.
Definition 2.4 A mapping 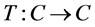 is said to be a quasi-G-asymptotically nonexpansive, if
is said to be a quasi-G-asymptotically nonexpansive, if  and there exists a sequence
and there exists a sequence  with
with  (as
(as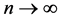 ), such that
), such that
 (8)
(8)
for any  and
and .
.
A mapping  is said to be a totally quasi-G-asymptotically nonexpansive, if
is said to be a totally quasi-G-asymptotically nonexpansive, if  and there exist sequences
and there exist sequences ,
, with
with  as
as  and a strictly increasing continuous function
and a strictly increasing continuous function  with
with , such that
, such that
 (9)
(9)
for all  and
and .
.
Remark 2.5 It is easy to see that a quasi- -asymptotically nonexpansive mapping is a quasi-G-asymptotically nonexpansive mapping with
-asymptotically nonexpansive mapping is a quasi-G-asymptotically nonexpansive mapping with  for all
for all . A totally quasi-
. A totally quasi- -asymptotically nonexpansive mapping is a totally quasi-G-asymptotically nonexpansive mapping with
-asymptotically nonexpansive mapping is a totally quasi-G-asymptotically nonexpansive mapping with . Therefore, our totally quasi-G-asymptotically nonexpansive mappings here are more widely than the totally quasi-
. Therefore, our totally quasi-G-asymptotically nonexpansive mappings here are more widely than the totally quasi- - asymptotically nonexpansive mappings which contain many kinds of generalized nonexpansive mappings as their special cases.
- asymptotically nonexpansive mappings which contain many kinds of generalized nonexpansive mappings as their special cases.
Definition 2.6 One-parameter family 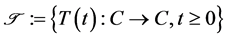 is said to be a quasi-G-asymptotically nonexpansive semigroup on
is said to be a quasi-G-asymptotically nonexpansive semigroup on , if the conditions (a)-(c) in Definition 1.2 and the following condition are satisfied:
, if the conditions (a)-(c) in Definition 1.2 and the following condition are satisfied:
(f) There exists a sequence  with
with  as
as  such that
such that
 (10)
(10)
holds for all ,
, .
.
One-parameter family 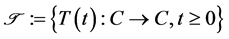 is said to be a totally quasi-G-asymptotically nonexpansive semigroup on
is said to be a totally quasi-G-asymptotically nonexpansive semigroup on , if the above conditions (a)-(c) in Definition 1.2 and the following condition are satisfied:
, if the above conditions (a)-(c) in Definition 1.2 and the following condition are satisfied:
(g) if  and there exist sequences
and there exist sequences ,
, with
with  as
as  and a strictly increasing continuous function
and a strictly increasing continuous function  with
with  such that for all
such that for all  and
and ,
,
 (11)
(11)
holds for each .
.
Remark 2.7 It is easy to see that a quasi- -asymptotically nonexpansive semigroup is a quasi-G-asymptotically nonexpansive semigroup with
-asymptotically nonexpansive semigroup is a quasi-G-asymptotically nonexpansive semigroup with  for all
for all . A totally quasi-
. A totally quasi- -asymptotically nonexpansive semigroup is a totally quasi-G-asymptotically nonexpansive semigroup with
-asymptotically nonexpansive semigroup is a totally quasi-G-asymptotically nonexpansive semigroup with .
.
When we use  instead of
instead of  in Definition 2.6 and denote
in Definition 2.6 and denote 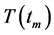 by
by ,
,  then a quasi-G-asymptotically nonexpansive semigroup becomes a countable family of total quasi-G-asymptotically nonexpansive mappings which contains a countable family of total quasi-
then a quasi-G-asymptotically nonexpansive semigroup becomes a countable family of total quasi-G-asymptotically nonexpansive mappings which contains a countable family of total quasi- -asymptotically nonexpansive mappings (see [3,4,7]) as it’s special case. So our totally quasi-G-asymptotically nonexpansive semigroup here is the most widely family of the nonexpansive mappings so far.
-asymptotically nonexpansive mappings (see [3,4,7]) as it’s special case. So our totally quasi-G-asymptotically nonexpansive semigroup here is the most widely family of the nonexpansive mappings so far.
The following Lemmas are necessary for proving the main results in this paper.
Lemma 2.8 [12] Let  be a uniformly convex and smooth Banach space, and
be a uniformly convex and smooth Banach space, and ,
,  be two sequences of
be two sequences of . If
. If  and either
and either  or
or  is bounded, then
is bounded, then .
.
Lemma 2.9 [13] If  is a strictly convex, reflexive and smooth Banach space, then for
is a strictly convex, reflexive and smooth Banach space, then for ,
,  if and only if
if and only if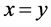 .
.
Lemma 2.10 [14] Let  be a real Banach space and
be a real Banach space and  be a lower semicontinuous convex functional. Then there exists
be a lower semicontinuous convex functional. Then there exists  and
and  such that
such that
 (12)
(12)
for each .
.
Lemma 2.11 [10] Let  be a real reflexive and smooth Banach space and
be a real reflexive and smooth Banach space and 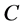 be a nonempty, closed and convex subset of
be a nonempty, closed and convex subset of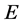 . Let
. Let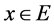 ,
, . Then
. Then
 (13)
(13)
Lemma 2.12 Let  be a uniformly smooth and strictly convex Banach space,
be a uniformly smooth and strictly convex Banach space,  be a nonempty closed and convex subset of
be a nonempty closed and convex subset of . Let
. Let 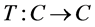 be a totally quasi-G-asymptotically nonexpansive mapping defined by (9). If
be a totally quasi-G-asymptotically nonexpansive mapping defined by (9). If , then the fixed point set
, then the fixed point set  of
of  is closed and convex subset of
is closed and convex subset of .
.
Proof Let  be a sequence in
be a sequence in  with
with  as
as , we prove that
, we prove that . In fact, since
. In fact, since  is a quasi-G-asymptotically nonexpansive mapping, we have
is a quasi-G-asymptotically nonexpansive mapping, we have

Since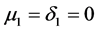 , it is equivalent to that
, it is equivalent to that

So,

By lemma 2.8, we have that  which implies that
which implies that  is closed. Next we prove that
is closed. Next we prove that  is convex, i.e. for any
is convex, i.e. for any ,
, 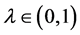 , we prove that
, we prove that . In fact,
. In fact,
 (14)
(14)
 (15)
(15)
Submitting (15) into (14), we have

This implies that  and
and . Hence we have
. Hence we have , i.e.
, i.e. . This completes the proof of Lemma 2.12.
. This completes the proof of Lemma 2.12.
3. Main Results
Theorem 3.1 Let E be a uniformly convex and uniformly smooth Banach space and  be a nonempty closed and convex subset of E. Let
be a nonempty closed and convex subset of E. Let  be a convex and lower semicontinuous function with
be a convex and lower semicontinuous function with 
such that  for all
for all  and
and . Let
. Let  be a closed and totally quasi-G-asymptotically nonexpansive semigroup defined by Definition 2.6. Assume that
be a closed and totally quasi-G-asymptotically nonexpansive semigroup defined by Definition 2.6. Assume that  is uniformly asymptotically regular for all
is uniformly asymptotically regular for all  and
and . Let the sequence
. Let the sequence  be defined by
be defined by
 (16)
(16)
where  and the sequence
and the sequence . If
. If  and
and then
then  converges strongly to
converges strongly to .
.
Proof We divide the proof into five steps.
Step 1. Firstly, we prove that  and
and 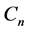 are closed and convex subsets in
are closed and convex subsets in .
.
Since  is a totally quasi-G-asymptotically nonexpansive mapping, it follows the Lemma 2.12 that
is a totally quasi-G-asymptotically nonexpansive mapping, it follows the Lemma 2.12 that  is a closed and convex subset of
is a closed and convex subset of . So
. So  is closed and convex subset of
is closed and convex subset of .
.
Again, by the assumption,  is closed and convex. Suppose that
is closed and convex. Suppose that  is the closed and convex subset of
is the closed and convex subset of  for
for . In view of the definition of
. In view of the definition of , we have that
, we have that

This shows that  is closed and convex for all
is closed and convex for all .
.
Step 2. Next, we prove that .
.
In fact, . Suppose that
. Suppose that , for some
, for some . Since
. Since  is a totally quasi-G-asymptotically nonexpansive semigroup, for each
is a totally quasi-G-asymptotically nonexpansive semigroup, for each , we have
, we have

where . This shows that
. This shows that , which implies that
, which implies that  for all
for all .
.
Step 3. We prove that  is bounded and
is bounded and 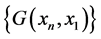 is convergent.
is convergent.
Since  is a convex and lower semicontinuous function, by virtue of Lemma 2.10, we have that there exists
is a convex and lower semicontinuous function, by virtue of Lemma 2.10, we have that there exists  and
and  such that
such that 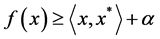 for each
for each . Then for each
. Then for each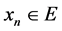 , we have that
, we have that
 (17)
(17)
Again since  and
and , from Lemma 2.11, we have
, from Lemma 2.11, we have  for any
for any
 . Hence, from (17), we have
. Hence, from (17), we have

Therefore  and
and  are bounded. As
are bounded. As  and
and , by using Lemma 2.11, we have that
, by using Lemma 2.11, we have that

This implies that  is bounded and nondecreasing. Hence the limit
is bounded and nondecreasing. Hence the limit  exists.
exists.
Step 4. Next, we prove that .
.
By the definition of , for any positive integer
, for any positive integer , we have
, we have . Again from Lemma 2.11, we have that
. Again from Lemma 2.11, we have that

as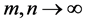 . It follows from Lemma 2.8 that
. It follows from Lemma 2.8 that . Hence
. Hence  is a Cauchy sequence in
is a Cauchy sequence in . Since
. Since  is a nonempty closed and convex subset of Banach space
is a nonempty closed and convex subset of Banach space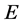 , we can assume that
, we can assume that . Therefore, we have
. Therefore, we have
 (18)
(18)
Since  and
and , it follows from the definition of
, it follows from the definition of  that we have
that we have


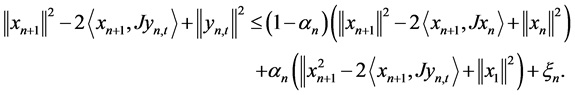
That is
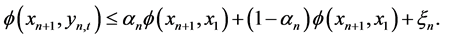 (19)
(19)
Since  and
and , from (18), (19), we can get
, from (18), (19), we can get

Then, by Lemma 2.8, we have
 (20)
(20)
As  is uniformly continuous on each bounded subset of
is uniformly continuous on each bounded subset of , we have
, we have . Then from (20), for any
. Then from (20), for any , we have
, we have

Since , we have that
, we have that

uniformly for all .
.
Since J is uniformly continuous, we obtain that
 (21)
(21)
uniformly for all .
.
Since  is asymptotically regular for all
is asymptotically regular for all , from (21), we have
, from (21), we have
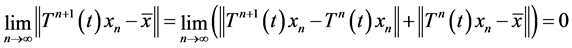
Then  as
as . By virtue of the closedness of
. By virtue of the closedness of  and
and 
as , we can obtain that
, we can obtain that , which implies
, which implies  for all
for all .
.
Hence, .
.
Step 5. Finally, we prove that .
.
Since  is closed and convex, by Lemma 2.2, we know that
is closed and convex, by Lemma 2.2, we know that  is single-valued.
is single-valued.
Assume that . Since
. Since  and
and , we have
, we have  for all
for all . As we know,
. As we know,  is convex and lower semicontinuous with respect to y when x is fixed. So we have
is convex and lower semicontinuous with respect to y when x is fixed. So we have

As , from the definition of
, from the definition of , we can obtain that
, we can obtain that 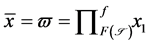 and
and  as
as
 . This completes the proof of Theorem 3.1.
. This completes the proof of Theorem 3.1.
Just as in Remark 2.7, we use  instead of
instead of  in Definition 2.6 and denote
in Definition 2.6 and denote  by
by ,
,  becomes a countable family of total quasi-G-asymptotically nonexpansive mappings. Then we get the following corollary.
becomes a countable family of total quasi-G-asymptotically nonexpansive mappings. Then we get the following corollary.
Corollary 3.2 Let  be a uniformly convex and uniformly smooth Banach space and
be a uniformly convex and uniformly smooth Banach space and  be a nonempty closed and convex subset of
be a nonempty closed and convex subset of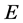 . Let
. Let  be a countable family of closed and totally quasi-Gasymptotically nonexpansive mappings. Let
be a countable family of closed and totally quasi-Gasymptotically nonexpansive mappings. Let  be a convex and lower semicontinuous function with
be a convex and lower semicontinuous function with  such that
such that  for all
for all 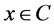 and
and . Assume that
. Assume that  is uniformly asymptotically regular for all
is uniformly asymptotically regular for all  and
and . Let the sequence
. Let the sequence 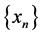 defined by
defined by
 (22)
(22)
where,  and
and . If
. If  and
and , then
, then 
converges strongly to .
.
In Corollary 3.2, when  for all
for all ,
,  be a countable family of closed and totally quasi-
be a countable family of closed and totally quasi- -asymptotically nonexpansive mappings. Then we can get the following theorem.
-asymptotically nonexpansive mappings. Then we can get the following theorem.
Corollary 3.3 Let  be a uniformly convex and uniformly smooth Banach space and
be a uniformly convex and uniformly smooth Banach space and  be a nonempty closed and convex subset of
be a nonempty closed and convex subset of . Let
. Let  be a countable family of closed and totally quasi-
be a countable family of closed and totally quasi- asymptotically nonexpansive mappings. Assume that
asymptotically nonexpansive mappings. Assume that  is uniformly asymptotically regular for all
is uniformly asymptotically regular for all 
and . Let the sequence
. Let the sequence  defined by
defined by
 (23)
(23)
where,  and
and . If
. If  and
and , then
, then 
converges strongly to .
.
Remark 3.4 The results in this paper improve and extend many recent corresponding main results of other authors (see, for example, [3,4,7,8,10,11,15-19]) in the following ways: (a) we introduce a new class of totally quasi-G-asymptotically nonexpansive mappings which contains the classes of the totally quasi- -asymptotically nonexpansive mappings and many non-expansive mappings; (b) we extend from a countable family of mappings to the totally quasi-G-asymptotically nonexpansive semigroup; (c) we modify the Halpern type hybrid projection algorithm by using the generalized f-projection operator for uniformly total quasi-G-asymptotically nonexpansive semigroup. For example, Corollary 3.2 extends the main result of Seawan et al. [11] from the modified Mann type iterative algorithm to modified Halpern iterative by the generalized f-projection method. Corollary 3.3 is the main result of Chang et al.[3].
-asymptotically nonexpansive mappings and many non-expansive mappings; (b) we extend from a countable family of mappings to the totally quasi-G-asymptotically nonexpansive semigroup; (c) we modify the Halpern type hybrid projection algorithm by using the generalized f-projection operator for uniformly total quasi-G-asymptotically nonexpansive semigroup. For example, Corollary 3.2 extends the main result of Seawan et al. [11] from the modified Mann type iterative algorithm to modified Halpern iterative by the generalized f-projection method. Corollary 3.3 is the main result of Chang et al.[3].
Contributions
All authors contributed equally and significantly in this research work. All authors read and approved the final manuscript.
Acknowledgements
The authors would like to thank editors and referees for many useful comments and suggestions for the improvement of the article. This study was supported by the National Natural Science Foundations of China (Grant No. 11271330) and the Natural Science Foundations of Zhejiang Province of China (Grant No. Y6110270).
NOTES
*Corresponding author.