Some Inequalities of Hermite-Hadamard Type for Functions Whose 3rd Derivatives Are P-Convex ()
1. Introduction
The following definition is well known in the literature.
Definition 1.1. A function  is said to be convex if
is said to be convex if
 (1.1)
(1.1)
holds for all .
.
In [1], the concept of the so-called  -convex functions was introduced as follows.
-convex functions was introduced as follows.
Definition 1.2. ([1]) We say that a map
 belongs to the class
belongs to the class  if it is nonnegative and satisfies
if it is nonnegative and satisfies
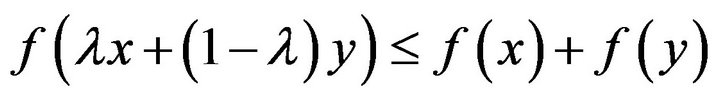 (1.2)
(1.2)
for all .
.
In [2], S. S. Dragomir proved the following theorems.
Theorem 1.1. ([2]) Let  be a differentiable mapping on
be a differentiable mapping on  and
and . If
. If 
is convex on , then
, then
 (1.3)
(1.3)
Theorem 1.2. ([2]) Let  be a differentiable mapping on
be a differentiable mapping on  and
and . If
. If  is convex on
is convex on  for
for , then
, then
 (1.4)
(1.4)
Theorem 1.3. ([3], Theorems 2) Let  be an absolutely continuous function on
be an absolutely continuous function on  such that
such that
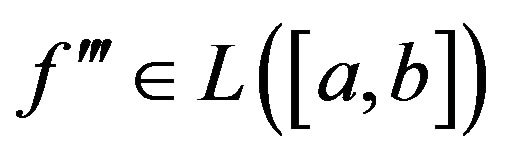 for
for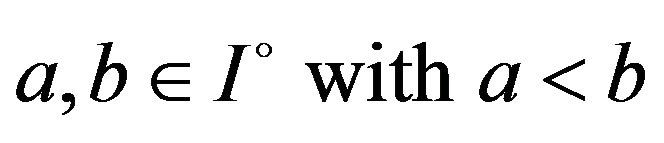 . If
. If  is quasi-convex on
is quasi-convex on , then
, then
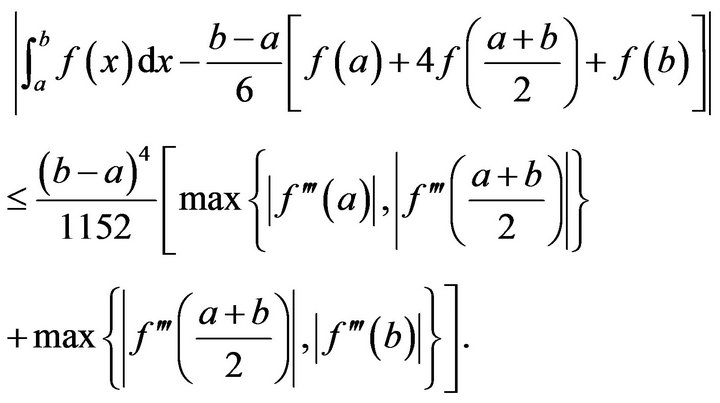
For more information and recent developments on this topic, please refer to [4-14] and closely related references therein.
The concepts of various convex functions have indeed found important places in contemporary mathematics as can be seen in a large number of research articles and books devoted to the field these days.
In this paper, we will establish some new HermiteHadamard type inequalities for functions whose  rd derivatives are P-convex.
rd derivatives are P-convex.
2. A Lemma
In this section, we establish an integral identity.
Lemma 2.1. Let  be a three times differentiable mapping on
be a three times differentiable mapping on  and
and . If
. If , then
, then
 (2.1)
(2.1)
Proof. Integrating by part and changing variable of definite integral yield

and

The proof of Lemma 2.1 is complete.
3. Hermite-Hadamard’s Type Inequalities for P-Convex Functions
Theorem 3.1. Let  be differentiable on
be differentiable on ,
, , and
, and 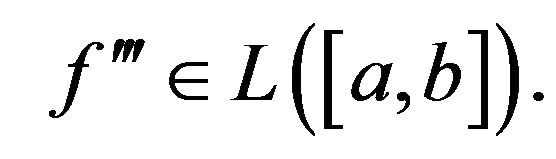 If
If  is
is  -convex on
-convex on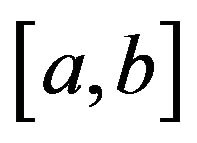 for
for , then
, then
 (3.1)
(3.1)
Proof. Since  is a
is a  -convex function on
-convex function on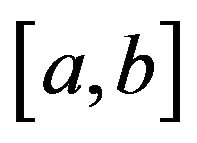 , by Lemma 2.1 and Hölder’s inequality, we obtain
, by Lemma 2.1 and Hölder’s inequality, we obtain

The proof of Theorem 3.1 is complete.
Corollary 3.1.1. Under the conditions of Theorem 3.1, if , we have
, we have

Theorem 3.2. Let  be differentiable on
be differentiable on ,
,  , and
, and . If
. If 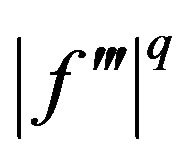 is
is  -convex on
-convex on  for
for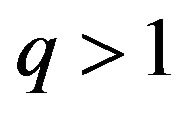 , then
, then
 (2.2)
(2.2)
Proof. From Lemma 2.1, Hölder’s inequality, and the 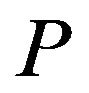 -convexity of
-convexity of  on
on , we drive
, we drive

Theorem 3.2 is proved.
Theorem 3.3. Let 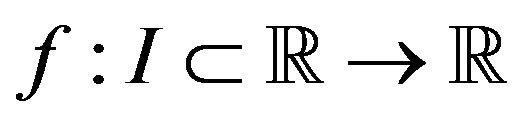 be differentiable on
be differentiable on ,
,  , and
, and  If
If  is
is 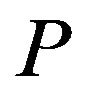 -convex on
-convex on for
for , then
, then
 (2.3)
(2.3)
Proof. From Lemma 2.1, Hölder’s inequality, and the 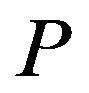 -convexity of
-convexity of 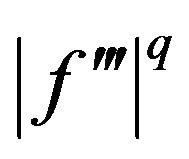 on
on , we have
, we have

Theorem 3.3 is thus proved.
Theorem 3.4. Let  be differentiable on
be differentiable on ,
, 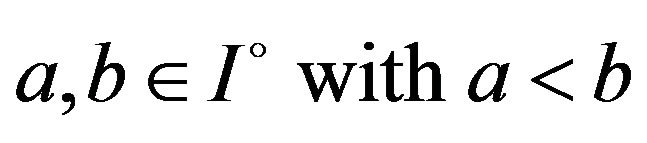 , and
, and  If
If  for
for  is
is  -convex on
-convex on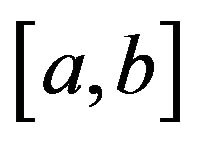 and
and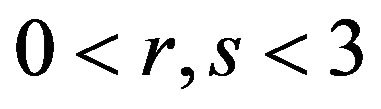 , then
, then
 (2.5)
(2.5)
Proof. Using Lemma 2.1, Hölder’s inequality, and the  -convexity of
-convexity of  on
on  yields
yields
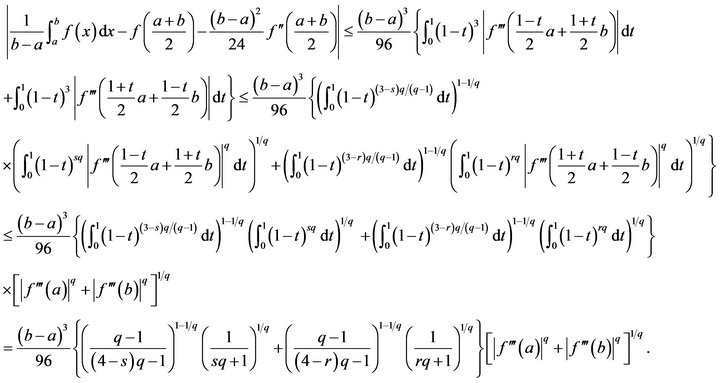
The proof of Theorem 3.4 is complete.
Corollary 3.3.1. Under the conditions of Theorem 3.4(1) if , then
, then
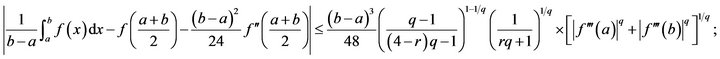
(2) if , then
, then

(3) if , then
, then

Finally we would like to note that these Hermite-Hadamard type inequalities obtained in this paper can be applied to the fields of integral inequalities, approximation theory, special means theory, optimization theory, information theory, and numerical analysis, as done before by a number of mathematicians.
4. Acknowledgements
The first two authors were partially supported by the Science Research Funding of Inner Mongolia University for Nationalities under Grant No. NMD1103.