Numerical Approach of Network Problems in Optimal Mass Transportation ()
1. Introduction
In this paper we present some models of urban planning. These models are examples of applications in mass transportation theory. They describe how to optimize the design of urban structures and their management under realistic assumptions. The paper is organized as follows: in Section 2 we present at first some urban planning models and preliminaries. The Section 3 is devoted to the approximation of the models; and numerical simulations that are our main results. Finally, summary and conclusions are presented in Section 4.
2. Preliminaries and Mathematical Modeling
Given two distributions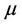 
and 
on 
with equal total mass, the classical generic Monge transportation problem consists in finding among all the maps 
verifying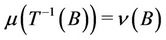 
for any measurable set in
, those which solve the minimization problem:
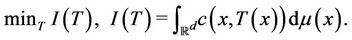
These maps are said to be transportation maps; they transport a measure 
(quantity) to a measure
.
For the existence of solutions, we recommend to see [6-10]. We invite the reader to see the books written in this topic by Villani [11,12] for additional information. In particularly Sudakov have studied in [13] the existence of optimal map transportation when 
and 
is absolutely continuous with respect to the Lebesgue measure
.
For studying the many cases where the Monge transportation problem doesn’t give a solution, Kantorovich considered the relaxed version of the Monge problem. In this framework, the transportation problem consists in finding among all admissible measures 
having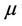 
and 
as marginals, those which solve the minimization problem
The meaning of the following expressions 
and 
is explained respectively as follows:
and 
for any measurable subset 
of
.
The Monge-Kantorovich problem obtained, depends only on the two distributions 
and
, and the cost 
which may be a function of the path connecting 
to
.
When the unknowns of the problem are the distributions 
and
, the Monge-Kantorovich mass transportation problemcan be interpreted as an optimal urban design problem. When the unknown is the transportation network, we have an irrigation problem, that is an optimal design of public transportation networks.
We also mention the dynamic formulation of mass transportation given in [4,14,15] and generalized in [16]. In this framework, we consider that:
· the space of measures acting is a time-space domain 
where the urban area 
is a bounded Lipschitz open subset with outward normal vector
;
· the mass density 
at the position 
and time 
is a Borel measure supported on
, i.e.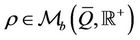
;
· the velocity field 
of a particle at 
is a Borel vectorial measures supported on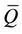
;
· the velocity field 
of the flow at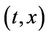 
is a Borel vectorial measures supported on 
and defined by 
.
The Monge-Kantorovich mass transportation problem consists in solving the following optimization problem:
(1)
with the constraints:
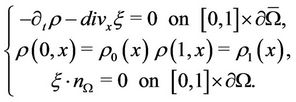(2)
where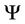 
is an integral functional on the 
-valued measures defined on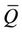
. Note that (2) is the continuity equation of our mass transportation model.
2.1. Optimal Urban Design
In the models of optimal design of an urban area we considered that
· the urban area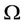 
is a well known regular compact subset of
;
· the total population and the total production are fixed data of the problem;
· only the density of residents 
and the density of services 
are unknowns data of the problem.
The aim is to find the density of residents 
and the density of services 
minimizing the transportation cost.
Principally there are two models for studying the optimal urban design. The first one takes into account the following facts:
· there is a transportation cost for moving from the residential areas to the services poles;
· people do not desire to live in areas where the density of population is too high;
· services need to be concentrated as much as possible, in order to increase efficiency and decrease management costs.
The transportation cost will be described through a Monge-Kantorovich mass transportation model.
In particularly, we will take it as the 
-Wasserstein distance defined by:
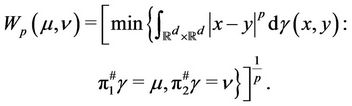
Taking into account the total unhappiness of residents due to high density of population, we define a penalization functional of the form
where 
is the density of the population, 
is supposed to be convex, null at the origin and super linear (that is 
as
). The increasing and diverging function 
represents the unhappiness to live in an area with population density
.
Thus we define a functional 
which penalizes sparse services. This functional is of the form:
where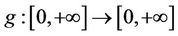 
is supposed to be concavenull with infinite slope at the origin (i.e. 
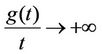as 
). Every single term 
in the sum above represents the cost for building and managing a service pole of size 
located at the point 
of
. The Report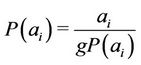 
is the productivity of pole of size
.
So in the first model, the optimal urban design problem becomes the following optimization problem:
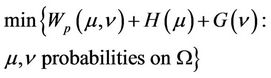(3)
In the second model the population transportation is considered as a flow, that is a vector field
. The equilibrium condition is achieved when the emerging flow is the excess of the demand in
, i.e.
In order to take into account the congestion effects, we suppose that the transportation cost 
per resident at the point 
depends on the traffic intensity at
, i.e.
where 
is an increasing function.
Then, the transportation cost moving 
to 
is:
The problem (1) with the constraints (2) allows both to take into account the congestion effects by an appropriated choice of the functionals 
and to widen the choice of unhappiness function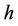 
and management cost function 
of the first model to the local lower semicontinuous functionals on
.
For more details, we refer the interested reader to the several recent papers on the subject (see for instance [4, 14-17]).
2.2. Network Problems Applied to the Urban Transportation
In the models of optimal design of an urban area we considered that
· the urban area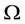 
is a well known regular compact subset of
;
· the density of residents 
and the density of services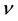 
are two well known positives measures with equal mass.
The irrigation problem consists to find among all feasible structures (or feasible network) 
those that minimize the transportation cost
The particular irrigation problem of the average distance consists to find an optimal network 
for which the average distance for a citizen to reach the mos 
t nearby point of the network is minimal.
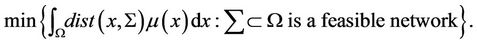
Theorem 1 For every 
there exists an optimal network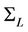 
for the Optimization problem
where 
is the Hausdorff measure defined on
.
Notice that there are other proposition of functionals to be minimized.
For more details, we refer the interested reader to the several recent papers on the subject (see for instance [1-3, 18,19]).
Our aim is to concentrate our effort on the numerical questions to locate the optimal network in a given domain 
says for example a town.
3. Approximation and Numerical Simulations
3.1. First Steps for the Formulation of the Discrete Problem
In this subsection, we are going to propose a first approach of discretization. From this, we deduce a generalized formulation but not the own possible formulation.
Let
For the simulation we are going to consider:
· 
and
;
· 
such that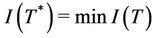
;
· a sequence of points 
and of balls 
such that
, with
, and
.
and let 
and
. We build an other map 
switching round cyclically the images of balls
. Then 
satisfies
where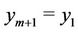 
and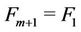
.
Then we have
, i.e.
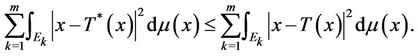
Therefore when
, we obtain
(4)
Suppose that the map 
and the measure 
are regular, the Equation (4) leads
(5)
Then 
is cyclically monotonous and
.
At first, in problem (
) the objective is to find the points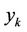 
which minimize
subject to
In the next section, we show that it is quite possible to give a more general approximation .
3.2. New Reformulation Using Permutations
In the literature, many formulations (see for example [1-4]) have not yet practical applications which deal with the permutation of points. In this paper we introduce a new reformulation of the problem by introducing permutations
.
Let us take a permutation 
defined on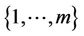 
such that
, we set:
and we solve the two following problems: (
)
subject to
and problem (
)
subject to
with the norm 
and
.
This is a theoretical formulation. And our aim is to apply it to a practical urban transport network. As a first step, we decided to work on 
with a reasonable number of points.
For a scenario in
, if we consider 
points: the number of programs to be solved becomes
. We leave the reader to verify that for:
· m = 3 points 
we solve 27 programs
· m = 4 points 
we solve 256 programs
· etc.
A scenario involving up to 18 points is used for problem (
). Using this scenario with problems (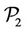
) and (
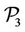) requires to solve 
programs, it is the reason we consider only some of these points for permutations in (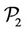
) and (
).
3.3. Numerical Experiments
This section shows how the three models developed in the two previous Sections 3.1 and 3.2 are applied to real data of Dakar Dem Dikk (3D). Recall that 3D (see [20], [21]) is the main public urban transportation company in Dakar. This company manages a fleet of buses with different technical characteristics. Some of the buses can operate only in certain roads in the city center and the others can access in all over the network. Buses are parked overnight at Ouakam and Thiaroye terminals (see Figure 1).
To ensure network coverage, 3D manages its services by using 17 lines, with 11 from Ouakam terminal and 6 from Thiaroye terminal. Each line ensures a certain num-
Figure 1. Urban transportation network of 3D.
ber of routes. At present, the total number of routes in the network is 289. First, the most important 18 sites of the network are identified. Thirty (30) permanent terminuses (terminals) and 810 bus stops are used (see Figure 1, where bus stops are not represented due to their size). The map in Figure 1 is obtained by using the software EMME [22]. Table 1 gives the 18 sites, their latitude and longitude.
The data are based on the scenario of 3D; and the input data needed to use the models are the:
· total length of the network 
kilometers;
· number of points 
(terminals and bus stops) 
(see Figure 1);
· latitude and longitude of points 
representing the two terminals and bus stops.
The total distance covered by all the buses from terminals to starting points of routes and from end points back to their terminals represents the total length of the network; and we have L = 5902.62 kilometers (for the 18 sites).
The GPS (Global Positioning System) coordinates are calculated with Google map, and then transformed into coordinates on the plane with he formula: degree + (minute/60) + (second/3600). Table 1 gives the coordinates of all points.
The numerical experiments are executed:
· on a computer: 2 × Intel(R) Core(TM)2 Duo CPU 2.00 GHz, 4.0 Gb of RAM, under UNIX system;
· and by the software IPOPT (Interior Point OPTimization) 3.9 stable [23,24], running with linear solver ma27.
For the objective function, we have:
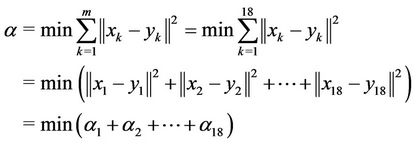
with
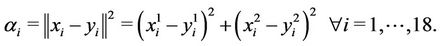
Finally,
and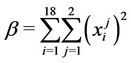 
is added to the value of the objective function.
Constraint 
gives
.
Urban transportation network of 3D Thus,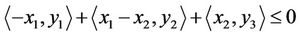 
, i.e.:
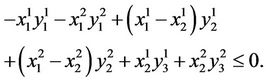
And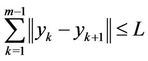 
gives
i.e.:
with 
and
.
We simply formulate the problem in AMPL [25] syntax, and solve the problem through the AMPL environment; with a total number of 38 variables for problem
. The solution obtained is an optimal one (for each case) wherein the priority is assigned to the minimization of the distance between 
and
. The IPOPT found an optimal point within desired tolerances; and we obtain the following results: the total number of iterations is 16 and for the optimal network 
we have
. The others obtained solutions
, 
and 
are given in Table 2 with the GPS coordinates. The points 
and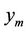 
are represented in the network (see Figure 2).
Permutations make the resolution more complicated but can give better results. The number of sub-problems to solve depends on the number of points in the network. Thus, we choose 
points in 3D’s network.
Now, let us take the permutation which is the main idea of this work. For problem
, 
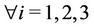such that
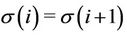, we have
. Therefore some constraints are similar and we have 9 subproblems to solve. An illustration:
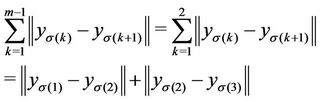
The three unconstrained sub-problems are obtained for 
with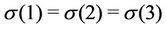
, i.e. in the three permutations (1,1,1), (2,2,2) and (3,3,3).
All sub-problems constraints are reported in Table 3.
Table 2. y1 and ym for optimal network Σopt.
Figure 2. Optimal network of 3D without permutation.
Table 3. All constraints with permutations.
It is sufficient to solve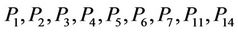 
and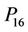
; since we have
, 
, 
, 
, 
, 
, 
, 
, 
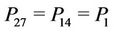and
.
We only compute the quantities
, 
and
. For all sub-problems
, the objective function is the same as problem 
with
.
with
,
and
.
Finally,
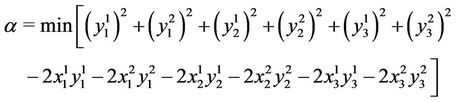
and 
is added to the value of the objective function.
From computational results, we have obtained the same value for all 10 sub-problems. Thus, permutations do not influence the distance constraint on the curve of
. The optimal value is 
for all 
with
.
For problem
, we consider 
and the number of possible permutation is
. Recall that the number of sub-problems to solve depends on the number of points in the network. Also, we choose 
points in 3D’s network. Thus, for the considered permutation 
we have obtained a total of 
sub-problems 
to solve, see Table 4.
In order not to overload explanations, we develop only the sub-problem
, the rest are left to the reader as an exercise.
In
, the sub-problem 
is obtained for
with vectors 
and 
. For the objective function, we have
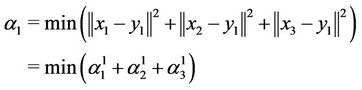
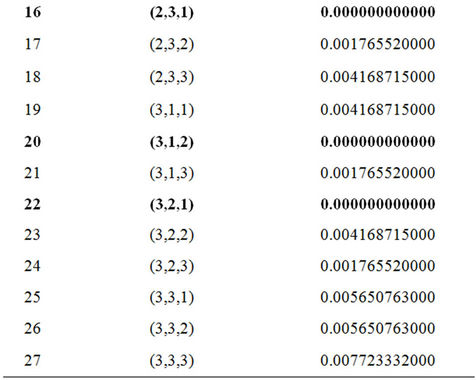
Table 4. Optimal values of αi with different permutations.
with
,
and
Finally,
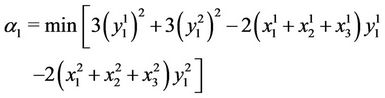
and 
is added to the value of the objective function for all sub-problems 
The constraint
gives
i.e.:
For the scenario of problems 
and
, we choose x1 = Ouakam terminal, x2 = Thiaroye terminal and x3 = Leclerc (see Table 5).
We denote by 
and 
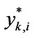the optimal value and the optimal solution of sub-problem 
, respectively.
The results show that the following six sub-problems:
, 
, 
, 
, 
, 
give the best value 
. The six solutions are different, i.e.:
with only
.
The curve 
can be described by one of the points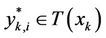
; see Figure 3 where
.
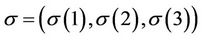The points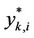 
which define 
(with coordinates 
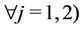are given in Table 6, with
.
The solutions giving the best possible permutations (optimum) are illustrated in Table 6 and include all permutations
.
According to the simulations, we determine a set of optimal policy that can describe the optimal network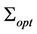
. Finally: after comparison of the simulated models, we can deduce that the model for problem 
is better. It provides the best curve describing the optimal value
, obtained with the permutations introduced in the objective function.
4. Conclusions
In this paper, we describe applications of mass transportation theory and develop how to optimize the curve design of urban network problems. Using the discrete formulations, we give three nonlinear programming problems with continue variables, and have described urban transportation problem of 3D applied to these three models. The results have shown that the optimal network is obtained with permutations including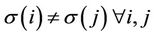
.
In future works, we will study an application in 
and make a reformulation that solves a unique program,
Table 5. The network Σopt with permutations.
Table 6. The optimal solutions 
with permutations.
5. Acknowledgements
We would like to thank all DSI’s (Division Système d’Information) members of 3D for their time and efforts for providing the data, and discussions related to the meaning of the data.