The Assessment of the Arising of Food Allergy among Antiacid Users Using Mathematical Model ()
1. Introduction
In 2001, Chiron et al. [1] described the first case of a new food allergy, an anaphylactic reaction to Manioc (Manihot esculenta or Manihot utilissima), also called cassava and tapioca. In 2004, Galvão et al. [2] described, nearly at the same time as a group of researchers from Portugal [3], the first case of cross-reactivity between cassava and natural rubber latex. Another case was reported by Ibero et al. [4]. Cassava is a tuber, rich source of carbohydrate widely consumed in Brazil and in more than 80 countries, mainly in South America, Asia and Africa. In Brazil, this food has been consumed since before the discovery of the country, by native Indians, i.e., more than 500 years ago, so why are the first cases just emerging now? A simple and superficial explanation would be a deficient diagnostics. However, this explanation is at least scarce giving that technical conditions and specific knowledge for a detailed diagnostics in allergy is available since years. Diagnostics in allergy evolved a lot in the last decades especially after description of IgE [5]. Furthermore, even earlier than development of specialized techniques medical literature already discussed clinical reports and therefore new allergies could be detected and diagnosed by clinicians. Accordingly, it seems that allergy to cassava is indeed a recent problem and considering the long period of consumption and population exposure to this food we can conclude that presumably one or more factors contributed to sensitization process and progression to allergy. In attempt to elucidate the problem our group investigated new cassava allergens from clinics to molecular biology, including the identification of a new allergen (the Man e 5) with cross reactivity to Hev b 5 from natural rubber latex [6].
Back to the fundamental question, why only now is this allergy been detected and the cases are increasing? One hypothesis that has been considered is the increasing use of proton pump inhibitors (PPIs) for digestive disorders [7]. This therapeutic class was introduced in 1988 and today they are among the most used drugs worldwide, including Brazil. Studies carried out by the group of HCUSP with this new allergen have demonstrated that this protein is part of a very special group of proteins called “natively unfolded or intrinsically unstructured” [8] that have been shown experimentally or are predicted to lack ordered structure [9]. These characteristics make it extremely labile to the action of the pepsin in the low pH of gastric juice, leading to its degradation in seconds (unpublished data). Antacid medications (PPIs) cause leaky gut syndrome, where food is absorbed before it is completely digested. This can result in both food allergies and immune exhaustion [10,11]. In this way, the elevation of the pH caused by PPIs results in maintenance of this cassava allergen intact, thereby facilitating its presentation to the immune system.
All the facts and evidences presented above lead us to a second question: why was allergy to cassava found in Brazil around 2002, if the PPIs were introduced around 14 years earlier in 1988? To answer this question we must consider some factors. From the beginning of the marketing of a new drug until the exponential growth in its use there is an elapse of time. In addition to this, new drugs with similar actions emerge. Moreover, we must consider that only part of the population uses the drug indiscriminately and irregularly, and that only part of it is genetically predisposed to sensitization. We must also take into consideration the time of sensitization to a new allergen and the period of time between the onset of symptoms and diagnosis.
The use of antiacids is triggered by a variety of conditions, ranging from stomach upset, heartburn, and nonulcer dyspepsia to verified gastric and duodenal ulcers. Antiacids have been found to be effective in the management of heartburn and ulcer dyspepsia and are also effective in the maintenance treatment of duodenal ulcer disease [12]. Drugs such as the H2-receptor antagonists, sucralfate, pirenzepine, and omeprazole, which have been introduced during the last 15 - 20 years, have to a great extent replaced antiacids in the treatment of peptic ulcer. The introduction during recent years of new treatment strategies that aim at the eradication of Helicobacter pylori may also have influenced the use of antiacids. However, the use of antiacids in less-severe forms of dyspepsia is very common, and antiacids still play a major role in the treatment of acid-related disorders [13]. Most dyspeptic symptoms are dealt with by patients, without seeking medical advice [14]. Corder et al. [15] have shown that the majority (80%) of those with dyspeptic complaints who did not consult a physician used simple antiacids. Furu and Straume [16] reported the overall prevalence of antiacid use about 10%, which is much higher than reported in a survey from Finland, in which only 3.7% reported use of antiacids [17].
Health surveys may collect information on nonprescription medications and also assess health status, risk factors, and sociodemographic variables at the individual level. Dyspepsia and related symptoms obviously represent the most common reason for the use of antiacids. However, there is reason to believe that additional factors such as general health status, lifestyle, and utilization of health services are associated with the use of antiacids, but no studies have explicitly tried to assess these associations [16]. Aiming to assess the risk of appearance of food allergy due to the increasing trend in the antiacid usage, we develop a mathematical model.
The paper is structured as follows. A simple mathematical model is developed aiming the assessment of the prevalence of food allergy among antiacid users (Section 2). We determine the steady states of the model, and the stability of the equilibrium points (Section 2). Also numerical results are presented with discussions (Section 3). Finally we present conclusion (Section 4).
2. Model
Our objective is the development of a simple mathematical model to describe the prevalence of food (cassava allergen) allergy in a population since the introducetion of antiacid by pharmaceutical industries. One of the effects of the antiacid is the elevation of pH in the stomach. As a consequence macro-proteins are not completely cleavage to aminoacids, and micro-proteins are absorbed by the surrounding epithelial cells and circulating immune cells (macrophages, dendritic cells, etc.) can recognize epitopes of these micro-proteins. In normal immune response, however, these epitopes are considered as self, and no immune reaction is promoted. Nevertheless, in some persons, the immune cells can be sensitized by epitopes, and, in conjunction with genetic predisposetion, environmental factors, etc., plasma cells are promoted to release antibodies (a comprehensive biological basis of food allergy can be found in [18]).
Our aim is to assess the prevalence of food allergy among persons in a community, rather than the individual development of the allergy [19]. A mathematical model is developed by assuming the following hypotheses.
Before the introduction of antiacid by pharmaceutical industries, we assume that there are not food (cassava allergen) allergic persons, and they are considered naive persons. The number of naive persons at time t is denoted by P. In a given time, antiacid medication is introduced in a completely naive population. Depending on the amount of budget applied by industries to promote the medicine, and on the efficacy of the antiacids, the number of antiacid users at time t, denoted by U, increases with time, but attains a saturation after a period of time due to, for instance, regulation of the medicine usage, less adherence of naive population, and even the limited capacity of production by pharmaceutical industries. We translate both features supposing that the incidence of new users is proportional to the numbers of naive persons and antiacid users, that is, . This kind of interacting function was used to describe the uptake of drugs by cancer cells [20]. The adherence to antiacid usage depends on the parameter
. This kind of interacting function was used to describe the uptake of drugs by cancer cells [20]. The adherence to antiacid usage depends on the parameter , named recruitment rate, and takes into account the marketing towards naive persons (P) and the efficacy measured by users (U). The recruitment of antiacid users follows mass action law for small number of antiacid users (
, named recruitment rate, and takes into account the marketing towards naive persons (P) and the efficacy measured by users (U). The recruitment of antiacid users follows mass action law for small number of antiacid users ( , for
, for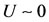 ) [21], but at increased number of users, the recruitment is saturated with respect to the users (
) [21], but at increased number of users, the recruitment is saturated with respect to the users ( , for
, for ). The parameter
). The parameter  is a scaling factor of recruitment: for lower values, the effect of saturation occurs very quickly, and the mass action law is practically absent (see Appendix A).
is a scaling factor of recruitment: for lower values, the effect of saturation occurs very quickly, and the mass action law is practically absent (see Appendix A).
Due to the residuals of micro-proteins (food allergens) in stomach which are absorbed by epithelial cells, immune system of antiacid users can be sensitized. This sensitization is strongly dependent on the amount of food allergens [22] that are presented to antigenic presenting cells (APC). In general there is a threshold of food allergens concentration that can effectively sensitize immune cells. These micro-biological behavior are translated to the populational sensitization by the factor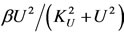 . The parameter
. The parameter  is the sensitization rate of antiacid users, which transfers these users to a group of sensitized persons (S, the number of sensitized persons at time t). The occurrence of sensitization is low for small number of antiacid users (
is the sensitization rate of antiacid users, which transfers these users to a group of sensitized persons (S, the number of sensitized persons at time t). The occurrence of sensitization is low for small number of antiacid users ( , for
, for ), but at increased number of users, the occurrence is saturated (
), but at increased number of users, the occurrence is saturated ( , for
, for ). This saturation is due to the threshold in the amount of food allergens in a person. The parameter
). This saturation is due to the threshold in the amount of food allergens in a person. The parameter  is a scaling factor of sensitization.
is a scaling factor of sensitization.
Among sensitized persons, due to genetic predisposetions, environment changes, etc., some individuals are actually driven to acquire immune response against food allergens. This biological event occurs less frequently than sensitization, hence we assume that acquisition of food allergy obeys . The parameter
. The parameter 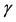 is the allergic reaction acquisition rate of sensitized persons, which transfers these individuals to a group of food allergic persons, denoted by A, the number of food allergic persons at time t. The occurrence of food allergy acquisition is very low for small number of sensitized persons (
is the allergic reaction acquisition rate of sensitized persons, which transfers these individuals to a group of food allergic persons, denoted by A, the number of food allergic persons at time t. The occurrence of food allergy acquisition is very low for small number of sensitized persons (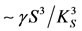 , for
, for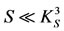 ), but at increased number of sensitized persons, the occurrence is saturated (
), but at increased number of sensitized persons, the occurrence is saturated ( , for
, for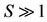 ). The parameter
). The parameter  is a scaling factor of food allergy acquisition.
is a scaling factor of food allergy acquisition.
Both sensitization and food allergy acquisition were described by Hill function of order n [23] (see Appendix A). In biochemistry, the binding of a ligand to a macromolecule is often enhanced if there are already other ligands present on the same macromolecule. In other words, once a ligand is bonded to the enzyme, its affinity for other ligand molecules increases. By using higher order for the allergy acquisition (n = 3) than sensitization of naive person (n = 2), we are assuming that there are much more factors needed to trigger allergic reaction than sensitization.
Besides the allergy acquisition parameters, we assume that all persons are under the same mortality rate , with
, with 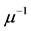 being the life expectancy. We also assume that antiacid users return to naive group at a rate
being the life expectancy. We also assume that antiacid users return to naive group at a rate  of abandonment of the medicine. We also assume that there is an effective treatment (when available) that cures allergic persons, and they return to sensitized group at a rate
of abandonment of the medicine. We also assume that there is an effective treatment (when available) that cures allergic persons, and they return to sensitized group at a rate 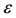 of treatment.
of treatment.
The above four sub-populations comprise a constant total population N = P + U + S + A. Let us define the proportions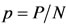 ,
,  ,
,  and
and , and new parameters
, and new parameters ,
,  and
and  . The per-capita scaling parameters
. The per-capita scaling parameters  and
and  are regarded to the critical values, while
are regarded to the critical values, while  does not bear this meaning, due to the linear relation (see Appendix A). For instance, there is a critical number
does not bear this meaning, due to the linear relation (see Appendix A). For instance, there is a critical number  such that for
such that for  sensitization is small, while for
sensitization is small, while for  it is big. Hence, if the scaling parameter
it is big. Hence, if the scaling parameter 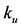 is big, the critical
is big, the critical  is big. The same argument is valid for allergy acquisition scaling parameter
is big. The same argument is valid for allergy acquisition scaling parameter .
.
Based on the above definitions of variables and model’s parameters, the dynamics of the food allergy acquisition is described by the following system of equations
 (1)
(1)
where . Dynamical trajectories are obtained using the following initial conditions (at
. Dynamical trajectories are obtained using the following initial conditions (at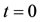 )
)
 (2)
(2)
which represents introduction of antiacid medication at  in a community previously free of this medicine. The initial value
in a community previously free of this medicine. The initial value  represents the proportion of persons who were coopted by intense marketing of pharmaceutical industries just before the introduction of antiacid.
represents the proportion of persons who were coopted by intense marketing of pharmaceutical industries just before the introduction of antiacid.
In Table 1 we present the summary of variables and parameters of the model.
Let us determine the steady states of the system of Equation (1), and assess the stability of these equilibrium

Table 1. Summary of the variables and parameters of the model.
points.
The steady states, denoted by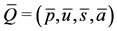 , can be determined by letting the derivatives equal to zero in the first members of the system (1). One of the steady states is the trivial equilibrium point
, can be determined by letting the derivatives equal to zero in the first members of the system (1). One of the steady states is the trivial equilibrium point  given by
given by
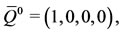 (3)
(3)
which corresponds to the population free of antiacids, hence free of food allergic persons.
To establish the stability of the trivial equilibrium point, we evaluate the eigenvalues of the characteristic equation associated to the matrix obtained by linearizing the system (1) around this equilibrium point. All eigenvalues will have negative real part if the Routh-Hurwitz criteria are satisfied [21]. Hence,  , is stable if
, is stable if , where
, where  is the threshold of
is the threshold of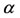 , and is given by
, and is given by
 (4)
(4)
(see Appendix B, where the global stability using Lyapunov function is also shown). If the rate of recruitment of naive individuals ( ) is lower than
) is lower than , then the antiacid users are going to extinction. As a pharmacological marketing point of view, the efficacy of a medicine must be confirmed by users who maintain the use. When
, then the antiacid users are going to extinction. As a pharmacological marketing point of view, the efficacy of a medicine must be confirmed by users who maintain the use. When , the trivial equilibrium becomes unstable, and the anti-acid users are sustained by the recruitment of naive persons.
, the trivial equilibrium becomes unstable, and the anti-acid users are sustained by the recruitment of naive persons.
Let us determine the non-trivial equilibrium point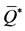 . From the first two equations of (1) in the steady state, we obtain
. From the first two equations of (1) in the steady state, we obtain
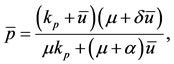 (5)
(5)
with  being the positive solution of the equation
being the positive solution of the equation
 (6)
(6)
where the rational functions  and
and  are
are

From the last two equations of (1) in the steady state, we obtain
 (7)
(7)
with 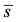 being the positive solution of the equation
being the positive solution of the equation
 (8)
(8)
where the rational functions  and
and  are, in terms of the previous solution
are, in terms of the previous solution ,
,
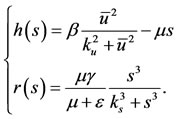
In Appendix B we present the analysis of Equations (6) and (8) with respect to the number of solutions: we have up to three positive solutions.
We next present numerical analysis regarded to the non-trivial equilibrium points. Also the system of Equations (1) is solved numerically in order to asses the time delay to occur the exponential growth phase of food allergy in a population.
3. Results and Discussion
The prevalence of antiacid users in 1996-1997 was higher than in 1987-1988 adjusted for age, gender and heartburn, and the proportion of antiacid users increased among those with dyspeptic complaints and also among those reporting no dyspeptic symptoms [24]. In this section we assess the prevalence of food allergy arising among antiacid users. First, we study the steady states; and, then, we determine numerically the dynamical trajectories of Equation (1). Discussions are also provided.
Numerical simulations are performed taking into account the values of the model’s parameters given in Table 2. The threshold of 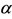 assumes
assumes 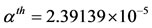
 , and the value of
, and the value of  is
is 
 . The units given in Table 2 are not shown hereafter.
. The units given in Table 2 are not shown hereafter.
3.1. Results Regarding to the Steady States
Using values given in Table 2, we show the bifurcation diagram in Figure 1: the positive solutions ,
, 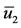 and
and  (labelled, respectively, as
(labelled, respectively, as ,
,  and
and ) as a function of
) as a function of . These values are positive solutions of Equation (6), which were numerically obtained by the bisection (to find zeros of polynomials) method [25]. For each
. These values are positive solutions of Equation (6), which were numerically obtained by the bisection (to find zeros of polynomials) method [25]. For each ,
, 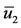 and
and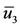 , we calculate other coordinates of the equilibrium points
, we calculate other coordinates of the equilibrium points ,
,  and
and , respectively, using Equation (B.2). The vertical axis begins at –0.1, because the small positive solution
, respectively, using Equation (B.2). The vertical axis begins at –0.1, because the small positive solution  assumes very lower values. The difference of magnitudes between
assumes very lower values. The difference of magnitudes between  and
and  are of some orders, which requires the use of log-scale (see figure below). In Figure 1 we show the coordinates at which we have two equilibrium points
are of some orders, which requires the use of log-scale (see figure below). In Figure 1 we show the coordinates at which we have two equilibrium points ,
, . At
. At  we have
we have  and
and  collapsing to
collapsing to  (decreasing values of
(decreasing values of ), and at
), and at  we have
we have  and
and  collapsing to
collapsing to  (increasing values of
(increasing values of ). Considering the values given in Table 2, and by solving Equation (B.1), we have:
). Considering the values given in Table 2, and by solving Equation (B.1), we have: 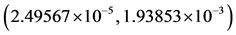 and
and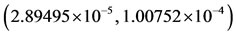 .
.
Figure 1 shows the hysteresis behavior. As α increases,  assumes very lower values (
assumes very lower values ( ). At
). At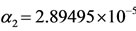 , at which we have
, at which we have , occurs a sudden jump to upper branch, and
, occurs a sudden jump to upper branch, and 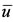 assumes very higher values (
assumes very higher values ( ). Conversely, as
). Conversely, as  decreases, for higher values of
decreases, for higher values of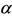 ,
,  assumes very higher values (
assumes very higher values ( ). At
). At  , at which we have
, at which we have , occurs a sudden jump to lower branch, and
, occurs a sudden jump to lower branch, and  assumes very lower values (
assumes very lower values ( ), reaching zero at
), reaching zero at . Many microorganisms present this kind of behavior, which is called quorum sensing [26].
. Many microorganisms present this kind of behavior, which is called quorum sensing [26].
Numerically it can be shown that the lower ( ) and upper (
) and upper ( ) branches are stable, while the intermediate branch (
) branches are stable, while the intermediate branch ( , defined in the interval
, defined in the interval ) is unstable (see Appendix B). Hence, the unstable equilibrium point
) is unstable (see Appendix B). Hence, the unstable equilibrium point  separates two region of attraction, depending on the initial conditions supplied to the dynamical system (1). Let us suppose that the initial conditions are the values of the coordinates of the equilibrium point
separates two region of attraction, depending on the initial conditions supplied to the dynamical system (1). Let us suppose that the initial conditions are the values of the coordinates of the equilibrium point , specially
, specially : if
: if , the equilibrium
, the equilibrium  is the attractor (regions labelled as II); while for
is the attractor (regions labelled as II); while for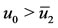 , the equilibrium
, the equilibrium  is the attractor (regions labelled as III). Disregarding the initial conditions, for
is the attractor (regions labelled as III). Disregarding the initial conditions, for ,
,  is the attractor, and for
is the attractor, and for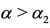 ,
,  is the attractor. Hence, the dynamics system attains one of the stable equilibrium points
is the attractor. Hence, the dynamics system attains one of the stable equilibrium points  and
and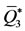 . Obviously, for
. Obviously, for  we have the trivial equilibrium point
we have the trivial equilibrium point  (region labelled
(region labelled
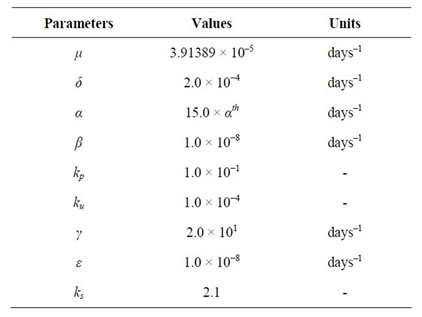
Table 2. Values for model’s parameters. Notice that the life expectancy is μ–1 = 70 years and the threshold value is αth = 2.39139 × 10–5 days–1.
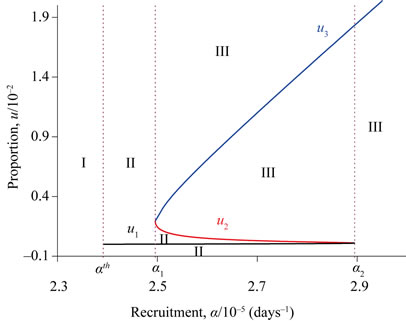
Figure 1. Bifurcation diagram obtained using values given in Table 2. The equilibrium points u1, u2 and u3 are labelled, respectively, as u1, u2 and u3. Considering the critical values α1 and α2, and the threshold αth, which is slightly smaller than α1, the attracting basins are labelled as I (all dynamical trajectories are attracted to the trivial ), II (all dynamical trajectories are attracted to
), II (all dynamical trajectories are attracted to ), and III (all trajectories are attracted to
), and III (all trajectories are attracted to ). In α1 < α < α2, the unstable equilibrium value
). In α1 < α < α2, the unstable equilibrium value  divides two attracting regions.
divides two attracting regions.
I) given by Equation (3), which is unique.
Figure 2 shows, using values given in Table 2, the stability of the equilibrium points ,
, 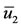 and
and . According to Routh-Hurwitz criteria for a second degree polynomial, if
. According to Routh-Hurwitz criteria for a second degree polynomial, if 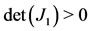 and
and , then the characteristic equation has eigenvalues with negative real part [21]. Figure 2(a) shows that
, then the characteristic equation has eigenvalues with negative real part [21]. Figure 2(a) shows that , for
, for 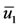 and
and , while for
, while for ,
, . Hence the small (
. Hence the small ( ) and big (
) and big (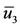 ) positive solutions are stable, while the intermediate root (
) positive solutions are stable, while the intermediate root ( ) is unstable. Notice that we have always
) is unstable. Notice that we have always  (Figure 2(b), showing that the stability is given by the term that does not depend on
(Figure 2(b), showing that the stability is given by the term that does not depend on  [27]). Also, from
[27]). Also, from 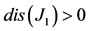 (Figure 2(c)), the eigenvalues corresponding to the matrix
(Figure 2(c)), the eigenvalues corresponding to the matrix  are real numbers, and dynamical trajectories do not have damped oscillations.
are real numbers, and dynamical trajectories do not have damped oscillations.
The real valued eigenvalues, due to  and
and , this according to Equation (B.6), state that the trajectories near the equilibrium points are node (if stable,
, this according to Equation (B.6), state that the trajectories near the equilibrium points are node (if stable,  or
or ) or saddle (if unstable,
) or saddle (if unstable, ) [21].
) [21].
Table 3 shows the variations of ,
,  ,
,  and
and  by varying the model’s parameters in 10 times. The range where three positive solutions occur increases with increasing in
by varying the model’s parameters in 10 times. The range where three positive solutions occur increases with increasing in  and
and , while with decreasing in
, while with decreasing in 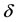 and
and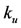 , the range increases. Hence, there are critical values
, the range increases. Hence, there are critical values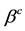 ,
,  ,
,  and
and  such that the hysteresis effects disappear (and, consequently, there is a unique positive solution for
such that the hysteresis effects disappear (and, consequently, there is a unique positive solution for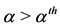 ). At the critical values
). At the critical values ,
, 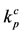 ,
,  and
and 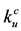 we must have
we must have  (and, conesquently,
(and, conesquently,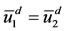 ), that is, Equation (B.1) has exactly one solution. However, for
), that is, Equation (B.1) has exactly one solution. However, for ,
,  ,
,  and
and , Equation (B.1) does not have positive solution in
, Equation (B.1) does not have positive solution in , and hysteresis is absent. Notice that the range of
, and hysteresis is absent. Notice that the range of 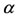 at which the hysteresis effects occurs is less sensitive than the jump between
at which the hysteresis effects occurs is less sensitive than the jump between 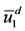 and
and . For instance, if we use
. For instance, if we use , (100 times lower than the value given in Table 2), we have
, (100 times lower than the value given in Table 2), we have ,
,  ,
,  and
and , and the quocients are
, and the quocients are  and
and .
.
Figure 3 shows the absence of the hysteresis effect, in which case we have the forward bifurcation (only one stable non-trivial equilibrium point  for
for ). Figure 3(a) shows the forward bifurcation, which was drawn using values given in Table 2, except
). Figure 3(a) shows the forward bifurcation, which was drawn using values given in Table 2, except , with
, with . Figure 3(b) shows the positive valued
. Figure 3(b) shows the positive valued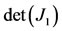 ,
,  and
and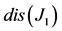 , hence this unique equilibrium point is stable.
, hence this unique equilibrium point is stable.
Antiacids have been available for many years, and are still commonly used self-prescribed drugs. However, their importance has diminished since the development of histamine-2-receptor antagonists (H2RA) and more recently proton pump inhibitors. Based on the drug wholesale statistics in Norway, the sale of antiacids decreased from 7.6 DDD/1000 inhabitants/day in 1988 to 4.3 DDD/1000 inhabitants/day in 1997. The H2RA and PPI have in the same period increased from 4.0 DDD/ 1000 inhabitants/day (only H2RA) in 1988 to 5.2 and 7.8 DDD/1000 inhabitants/day in 1997, respectively. The unit of measurement in wholesale statistics is usually the Defined Daily Dose (DDD), which is defined as the assumed average maintenance dose per day for a drug use on its main indication in adults [24]. Health surveys may, however, collect information on nonprescription medications and also assess health status, risk factors, and sociodemographic variables at the individual level [16]. In

Figure 3. Forward bifurcation diagram (a) obtained using values given in Table 2, except β = 1.0 × 10−9. Determinant, trace and discriminant of J1 corresponding to the unique  are positive (b).
are positive (b).
this way we assessed the hazard of food allergy originating from self-care use of antiacids.
How could nonprescription medications be managed after proving dangerous (in different levels) side effects? Let us drawn the log-scale bifurcation diagram using values given in Table 2, except higher 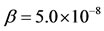 and lower
and lower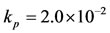 . In Figure 4 the equilibrium points (as a function of
. In Figure 4 the equilibrium points (as a function of )
) ,
,  and
and  are labelled, respectively, as
are labelled, respectively, as ,
, 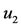 and
and . We also show the critical values
. We also show the critical values  and
and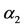 , and the threshold
, and the threshold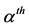 , which are lower than those obtained in Figure 1. The arrows indicate the attracting equilibrium values (stable equilibrium point
, which are lower than those obtained in Figure 1. The arrows indicate the attracting equilibrium values (stable equilibrium point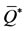 ). The intervals of the recruitment rate
). The intervals of the recruitment rate 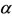 are:
are: 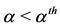 (I),
(I), 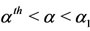 (II),
(II),  (III) and
(III) and 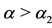 (IV). The arrows indicate the attracting equilibrium values (stable equilibrium point
(IV). The arrows indicate the attracting equilibrium values (stable equilibrium point ). Next we present some scenarios regarding to the control of the use of nonprescription medications. The discussions can be promptly applied to antiacids.
). Next we present some scenarios regarding to the control of the use of nonprescription medications. The discussions can be promptly applied to antiacids.
Figure 4 shows an obvious finding: the rate at which naive person becomes nonprescription medications user  is the main control parameter. When the use is spread throughout the community for diversity of reasons, which case corresponds to the case
is the main control parameter. When the use is spread throughout the community for diversity of reasons, which case corresponds to the case  (region labelled as IV in Figure 4), the prevalence of users situates at very high level (
(region labelled as IV in Figure 4), the prevalence of users situates at very high level ( ). Let us suppose that a campaign is carried on in order to avoid self-care use of medications, which decreases the recruitment of users (
). Let us suppose that a campaign is carried on in order to avoid self-care use of medications, which decreases the recruitment of users ( decreases). First, if this rate of the recruitment is still elevated (
decreases). First, if this rate of the recruitment is still elevated ( , region IV), a decreasing in the amount of users due to health campaign is temporary, and as time goes on, the previous prevalence is attained. In other words, a complete rejection of medications is only possible with the abandonment of medications by all users (
, region IV), a decreasing in the amount of users due to health campaign is temporary, and as time goes on, the previous prevalence is attained. In other words, a complete rejection of medications is only possible with the abandonment of medications by all users ( ). Second, when the recruitment is lowered substantially (
). Second, when the recruitment is lowered substantially ( , region III), if the educational campaign reduces the users below the critical proportion (
, region III), if the educational campaign reduces the users below the critical proportion ( ), then, as time goes on, the prevalence is decreased dramatically reaching low value
), then, as time goes on, the prevalence is decreased dramatically reaching low value  (order of
(order of ). Third, if adherence to campaign is elevated, (
). Third, if adherence to campaign is elevated, ( , region II), the prevalence situates at low value
, region II), the prevalence situates at low value . Notice an abrupt jump down of users at
. Notice an abrupt jump down of users at . Finally, in the region I (
. Finally, in the region I ( ), a perfect campaign reduced the recruitment rate below its threshold, and as time goes on, all individuals abandon the use of medications.
), a perfect campaign reduced the recruitment rate below its threshold, and as time goes on, all individuals abandon the use of medications.
With respect to the nonprescription antiacids, which can induce food allergy, public health authorities must design a campaign that reduces the recruitment rate below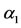 , without the necessity of reaching all persons (
, without the necessity of reaching all persons ( ). If this goal is unreachable, a campaign must reduce the recruitment rate below
). If this goal is unreachable, a campaign must reduce the recruitment rate below , and additional efforts must be spent to reduce the antiacid users below the critical value (
, and additional efforts must be spent to reduce the antiacid users below the critical value ( , coordinate of the stable equilibrium
, coordinate of the stable equilibrium ). The reason is due to the fact that the preva-
). The reason is due to the fact that the preva-
lence  (coordinate of the stable equilibrium
(coordinate of the stable equilibrium ) is so low that avoids the appearance of food allergic persons.
) is so low that avoids the appearance of food allergic persons.
3.2. Dynamical Trajectories
Steady states analysis furnished qualitative behavior of the system of Equations (1). Numerical solutions of this system of ordinary differential equations were obtained by the 4th order Runge-Kutta method [25]. In appropriate ranges of values of the model’s parameters, we can observe the hysteresis behavior. Now let us determine the period of time spent in order to appear cases of cassava allergic persons in a measurable prevalence.
The system of Equation (1) is divided into two subsystems: the first two equations describing the recruitment of persons to become antiacid users, and the last two equations, which is feed by the first sub-system, describing the onset of food allergy among antiacid users. The parameters regarded to the first sub-system determine the qualitative behavior of the dynamical system: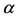 ,
,  ,
,  ,
, 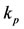 and
and . The remaining parameters
. The remaining parameters ,
,  and
and  can be managed to assess the food allergy manifestation in a community. Both sub-systems are coupled by the parameters
can be managed to assess the food allergy manifestation in a community. Both sub-systems are coupled by the parameters  and
and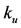 .
.
The following numerical results are obtained changing the values of the parameters  and
and  given in Table 2:
given in Table 2:  and
and . These values are those used to draw the bifurcation diagram given in Figure 4. The threshold value becomes
. These values are those used to draw the bifurcation diagram given in Figure 4. The threshold value becomes , and hence
, and hence . In this case, we have
. In this case, we have ,
, 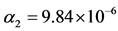 ,
,  and
and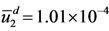 , and the quocients are
, and the quocients are  and
and .
.
Let us assume that 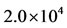 persons were convinced by pharmaceutical industries to use antiacid when it was released. If we assume a total population of
persons were convinced by pharmaceutical industries to use antiacid when it was released. If we assume a total population of 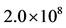 persons, like Brazil, the initial conditions, given by Equation (2), supplied to the dynamical system (1) are
persons, like Brazil, the initial conditions, given by Equation (2), supplied to the dynamical system (1) are ,
,  , and
, and  . The latter initial conditions describe, due to the absence of PPIs, the absence of sensitized persons neither persons who acquired food allergy. Figure 5 shows the dynamical trajectories: long-term Figure 5(a) and short-term Figure 5(b). The year 0 in the simulations can be linked to the year 1988, when PPIs were introduced. Fifteen years later since the introduction of antiacid in a community, we have 8 cases of food allergy in a population of 200 million persons, and asymptotically attains 92 cases per 1 million persons (equilibrium value
. The latter initial conditions describe, due to the absence of PPIs, the absence of sensitized persons neither persons who acquired food allergy. Figure 5 shows the dynamical trajectories: long-term Figure 5(a) and short-term Figure 5(b). The year 0 in the simulations can be linked to the year 1988, when PPIs were introduced. Fifteen years later since the introduction of antiacid in a community, we have 8 cases of food allergy in a population of 200 million persons, and asymptotically attains 92 cases per 1 million persons (equilibrium value ). With respect to sensitized persons, we find 48,000 cases after fifteen years in a population of 200 million persons, and asymptotically attains 1200 cases per 1 million persons (equilibrium value
). With respect to sensitized persons, we find 48,000 cases after fifteen years in a population of 200 million persons, and asymptotically attains 1200 cases per 1 million persons (equilibrium value ).
).
If we increase the initial conditions to  and
and , 8 cases of food allergy in a population of 200 million persons are observed after elapsing 14.57 and 14.52 years, respectively. For decreased initial condition
, 8 cases of food allergy in a population of 200 million persons are observed after elapsing 14.57 and 14.52 years, respectively. For decreased initial condition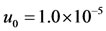 , 8 cases of food allergy in a population of 200 million persons are observed after elapsing 16.4 years. The asymptotic (equilibrium) proportions of the naive persons
, 8 cases of food allergy in a population of 200 million persons are observed after elapsing 16.4 years. The asymptotic (equilibrium) proportions of the naive persons 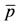 and PPIs users
and PPIs users  are near, respectively, 0.8 and 0.2 (Figure 5(a)). The value assigned to
are near, respectively, 0.8 and 0.2 (Figure 5(a)). The value assigned to  is much higher than
is much higher than , hence we have only one equilibrium point
, hence we have only one equilibrium point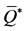 . In this case, the initial conditions only affect the delay in the time of arising of the exponential growth, and further achievement of asymptotic equilibrium.
. In this case, the initial conditions only affect the delay in the time of arising of the exponential growth, and further achievement of asymptotic equilibrium.
Now, let us illustrate the dependency of the dynamical system with the initial conditions, letting to 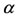 a value situated between
a value situated between  and
and , that is,
, that is, . At this value, we have
. At this value, we have ,
,  and
and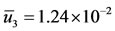 . The initial conditions supplied to the system (1) are given by Equation (2). For the initial condition
. The initial conditions supplied to the system (1) are given by Equation (2). For the initial condition  (Figure 6(a)), dynamical trajectories are attracted to the equilibrium point
(Figure 6(a)), dynamical trajectories are attracted to the equilibrium point , with coordinates obtained using
, with coordinates obtained using , according to Equation (B.2). However, for
, according to Equation (B.2). However, for  (Figure 6(b)), dynamical trajectories are attracted to the equilibrium point
(Figure 6(b)), dynamical trajectories are attracted to the equilibrium point , with coordinates obtained using
, with coordinates obtained using . The unstable equilibrium point
. The unstable equilibrium point  is called break point [28]. Notice that both
is called break point [28]. Notice that both  are lower than
are lower than ; because we used
; because we used  instead of
instead of 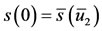 and
and  .
.
All preceding results were obtained assuming that the values of the model’s parameters are fixed, that is, they

Figure 5. Long-term (a) and short-term (b) dynamical trajectories using values given in Table 2, except β = 5.0 × 10−8 and kp = 2.0 × 10−2.
do not vary with time. The autonomous dynamic system presented a threshold 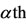 in the bifurcation diagram, besides the hysteresis behavior. The threshold
in the bifurcation diagram, besides the hysteresis behavior. The threshold  appeared due to the mass action law approximation for small number of antiacid users (
appeared due to the mass action law approximation for small number of antiacid users (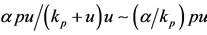 in the dynamics system) [27]. The hysteresis reports a social behavior in which a critical number of persons (in our example, the use of antiacids) is needed to trigger an intense collective response.
in the dynamics system) [27]. The hysteresis reports a social behavior in which a critical number of persons (in our example, the use of antiacids) is needed to trigger an intense collective response.
4. Conclusions
We developed a simple phenomenological model to describe the appearance of food allergy (cassava allergen) in persons who are users of antiacids. Our argument was that the increasing use of proton pump inhibitors for digestive disorders resulted in the elevation of the pH, and, consequently, the cassava allergen remains intact, thereby

Figure 6. Dependence of the dynamical trajectories with the initial conditions using values given in Table 2, except α = 8.0 × 10−6, β = 5.0 × 10−8 and kp = 2.0 × 10−2. For u (0) = u0 = 2.8794 × 10−4 dynamical trajectories are attracted to  (a), while for u0 = 2.8795 × 10−4, to
(a), while for u0 = 2.8795 × 10−4, to  (b).
(b).
facilitating its presentation to the immune system. Additionally, only part of it uses the drug indiscriminately and irregularly, and that only part of the population is genetically predisposed to be sensitized and acquire food allergy. We expect however an elapse in the time from the introduction of antiacids (specially PPIs) until the sensitization to a new allergen, the onset of symptoms and diagnosis of food allergy.
The model considered Hill function to describe the following events: 1) the recruitment of naive persons to become antiacid users ( ); 2) the sensitization of the immune system among antiacid users to the cassava allergen remained intact due to the elevation of pH (
); 2) the sensitization of the immune system among antiacid users to the cassava allergen remained intact due to the elevation of pH (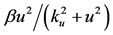 ); and 3) the onset of symptoms of food allergy (
); and 3) the onset of symptoms of food allergy ( ). The reason behind the choice of Hill type function was basically of three types: 1) non-prescription medicines (like antiacids) usage can be thought of social behavior (collective response depends on a critical number of adhered persons); 2) the sensitization is strongly dependent on a threshold in the amount of food allergens; and 3) the acquisition of allergy is an event depending on many factors, such as genetic predisposition, modern life style including social behavior and food intake, and stress.
). The reason behind the choice of Hill type function was basically of three types: 1) non-prescription medicines (like antiacids) usage can be thought of social behavior (collective response depends on a critical number of adhered persons); 2) the sensitization is strongly dependent on a threshold in the amount of food allergens; and 3) the acquisition of allergy is an event depending on many factors, such as genetic predisposition, modern life style including social behavior and food intake, and stress.
Due to the mass action law, there was a threshold of the recruitment rate 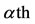 below which the antiacid users cannot be maintained. The use of Hill function to describe the flow between different status of persons in a community arose the hysteresis behavior, which appears when
below which the antiacid users cannot be maintained. The use of Hill function to describe the flow between different status of persons in a community arose the hysteresis behavior, which appears when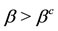 ,
,  ,
, 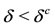 and
and . Hysteresis effects consisted in the appearance of three equilibrium points
. Hysteresis effects consisted in the appearance of three equilibrium points ,
,  and
and 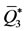 in the interval
in the interval  in such way that, as
in such way that, as 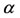 increases, small positive solution
increases, small positive solution  (coordinate of
(coordinate of ) jumped suddenly at
) jumped suddenly at 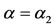 to big positive solution
to big positive solution 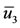 (coordinate of
(coordinate of ). The positive solutions
). The positive solutions  and
and  assume very small values, while
assume very small values, while  does not. Dynamically, the trajectories are attracted either
does not. Dynamically, the trajectories are attracted either  or
or  depending on the initial conditions supplied to the dynamical system (Figure 6). When the recruitment rate situates between
depending on the initial conditions supplied to the dynamical system (Figure 6). When the recruitment rate situates between  and
and , or
, or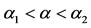 , if the initial amount of antiacid users (u0) does not achieve a critical value (regarded to the coordinates of the unstable
, if the initial amount of antiacid users (u0) does not achieve a critical value (regarded to the coordinates of the unstable ), this community is relatively safe from onset of allergic reactions in persons. However, the figure is completely different if u0 surpasses the critical value: the number of antiacid users increases around 345 times for
), this community is relatively safe from onset of allergic reactions in persons. However, the figure is completely different if u0 surpasses the critical value: the number of antiacid users increases around 345 times for  (Figure 6). In the situation as reported by Figure 6 (low value of recruitment rate), the pharmaceutical industry must spent a lot of money to convince people to use antiacids. If this goal is successful, then the possibility of appearing food allergy is increased dramatically.
(Figure 6). In the situation as reported by Figure 6 (low value of recruitment rate), the pharmaceutical industry must spent a lot of money to convince people to use antiacids. If this goal is successful, then the possibility of appearing food allergy is increased dramatically.
Population-based information showed that the consumption of antiacids, which are nonprescription drugs, mainly is explained by the prevalence of dyspeptic symptoms. Nonprescription antiacid medication, in conjunction with the report of some degree of relief in the treatment of acid-related disorders by users, can increase the recruitment rate . A larger number of medical visits in the year 1987-1988 predicted an increased likelyhood of being an antiacid user, and this findings persisted throughout the period [16]. When
. A larger number of medical visits in the year 1987-1988 predicted an increased likelyhood of being an antiacid user, and this findings persisted throughout the period [16]. When 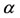 increases and surpasses the critical value
increases and surpasses the critical value , that is,
, that is, 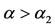 , the dynamical trajectories are driven to the big equilibrium
, the dynamical trajectories are driven to the big equilibrium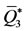 , regardless the initial conditions supplied to the dynamical system. Therefore, food allergy originated from cassava allergen can be detectable if the recruitment rate
, regardless the initial conditions supplied to the dynamical system. Therefore, food allergy originated from cassava allergen can be detectable if the recruitment rate  is situated above the critical value
is situated above the critical value , rather than the threshold
, rather than the threshold  (Figure 5).
(Figure 5).
From the dynamical trajectories of the model (Figure 5), we conclude that detectable number of patients should be arose 15 years after the introduction of antiacids, which was in 1988. Hence, in the year 2003 first cases of food allergy from antiacid users should be diagnosed. After 23 years, in the calendar year of 2011, we can estimate the incidence of sensitized and food allergic persons in 3500 and 2 cases per 10 million persons, respectively. These estimates were obtained using the values given in Table 2, except  and
and . Other sets of values can be provided to the model’s parameters in order to estimate different outcomes. However, there are a complete lack of reliable estimatives in a population level to be compared with the model’s prediction. The food allergy may become a public health problem, if PPIs are being used indiscriminately and irregularly. The results obtained from the analysis of the model suggest that the use of nonprescription antiacids, like PPIs, may be recommended or approved by the physician in order to avoid the rising of food allergy.
. Other sets of values can be provided to the model’s parameters in order to estimate different outcomes. However, there are a complete lack of reliable estimatives in a population level to be compared with the model’s prediction. The food allergy may become a public health problem, if PPIs are being used indiscriminately and irregularly. The results obtained from the analysis of the model suggest that the use of nonprescription antiacids, like PPIs, may be recommended or approved by the physician in order to avoid the rising of food allergy.
Finally, as new biological findings occur, improved mathematical model can be developed and fitted against observed data. Notwithstanding, the simple model we developed and analyzed here showed an elapse of 15 years from the introduction of antiacid medicine before the onset of food allergic persons, and the model is forecasting an exponential growth in the number of food allergic persons currently.
5. Acknowledgements
This work was supported by a grant from FAPESP (Projeto Temático, 09/15098-0). HMY gratefully acknowledges a Fellowship awarded by CNPq.
Appendix A. Hill Function
Let us consider the Hill function [23] of order n, written as

The first derivative of the Hill function is  , and the second derivative is
, and the second derivative is  for
for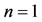 , and
, and
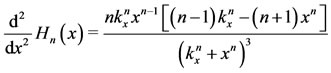
for . Notice that for
. Notice that for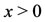 , the first derivative is always positive, and
, the first derivative is always positive, and  is strictly increasing function from
is strictly increasing function from 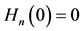 to
to .
.
The first order Hill function (n = 1) is increasing function without change of concavity. However, for , the increasing n-th order Hill function changes the concavity at
, the increasing n-th order Hill function changes the concavity at , that is,
, that is,
 , and the value of
, and the value of  at
at 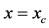
is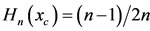 . For
. For , the concavity is upward (
, the concavity is upward (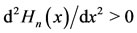 ); conversely, downward for
); conversely, downward for . Clearly, the inflexion point
. Clearly, the inflexion point  exists only for
exists only for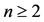 .
.
The coordinates of the inflexion point for  is
is , while for
, while for , we have
, we have . Notice that, as n increases,
. Notice that, as n increases,  and
and  increase, the first from
increase, the first from  to a, while the latter from 1/4 to 1/2.
to a, while the latter from 1/4 to 1/2.
Figure A1 illustrates the Hill function for , 2 and 3, letting an arbitrary value
, 2 and 3, letting an arbitrary value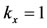 . At
. At , we have
, we have , for all n. Notice that, for
, for all n. Notice that, for , if
, if , we have
, we have , while for
, while for ,
, .
.
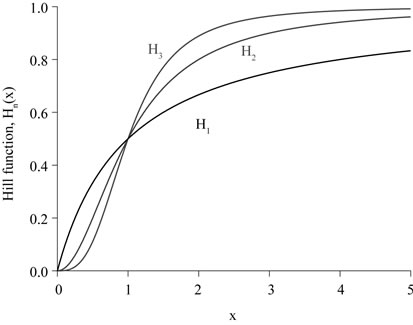
Figure A1. Hill function for the first three degrees, with Hn (Kx) = 0.5 at x = Kx = 1.
Appendix B. Analysis of the Model We deal with the steady states of the system (1), and we assess the stability of the equilibrium points.
1.1. Steady States
The trivial equilibrium point 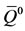 is given by Equation (3). The non-trivial equilibrium point
is given by Equation (3). The non-trivial equilibrium point  has the coordinates given by: Equation (5) for
has the coordinates given by: Equation (5) for , solution (s) of Equation (6) for
, solution (s) of Equation (6) for , solution of Equation (8) for
, solution of Equation (8) for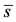 , and Equation (7) for
, and Equation (7) for . Hence, let us analyze Equations (6) and (8).
. Hence, let us analyze Equations (6) and (8).
From Equation (6), the function 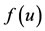 is such that
is such that
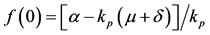 ,
,
 ,
,  at
at
 , and
, and

where . If
. If , we have
, we have , where
, where  is given by Equation (4). However, for
is given by Equation (4). However, for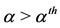 ,
,  is a strictly decreasing function with upward concavity, and assumes positive values in the interval
is a strictly decreasing function with upward concavity, and assumes positive values in the interval . Summarizing,
. Summarizing, 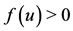 is strictly decreasing for
is strictly decreasing for 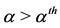 and
and  .
.
The function  is such that
is such that ,
,  , and
, and

Hence,  for
for , and has a maximum at
, and has a maximum at  (
( increases for
increases for , and decreases for
, and decreases for ), and changes the concavity at
), and changes the concavity at  (downward concavity for
(downward concavity for , and upward concavity for
, and upward concavity for ).
).
By comparing the behaviors of the functions 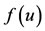 and
and , we conclude that a positive solution always exists for
, we conclude that a positive solution always exists for , that is,
, that is, . This inequality is just the condition for the trivial equilibrium becoming unstable. Notice that
. This inequality is just the condition for the trivial equilibrium becoming unstable. Notice that  is a function of
is a function of , while
, while  is a function of
is a function of . Let us fix the value of
. Let us fix the value of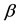 , and vary
, and vary . Let us define two values
. Let us define two values 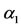 and
and  (see below), with
(see below), with , and analyze the equation
, and analyze the equation 
 . For small values of α, but greater than the threshold
. For small values of α, but greater than the threshold , that is,
, that is, 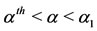 , Equation (6) has only one positive solution, such that
, Equation (6) has only one positive solution, such that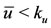 . As α increases (
. As α increases (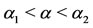 ), Equation (6) has three positive solutions such that
), Equation (6) has three positive solutions such that ,
,  and
and . Finally, for sufficiently higher values of
. Finally, for sufficiently higher values of  (
( ), Equation (6) has again a unique positive solution, such that
), Equation (6) has again a unique positive solution, such that . We stress the fact that
. We stress the fact that  is always a solution whatever be the value of
is always a solution whatever be the value of . Similar behavior occurs when we fix
. Similar behavior occurs when we fix  and vary
and vary .
.
The passage from one solution to three positive solutions, or vice-versa, as  varies, occurs at values of
varies, occurs at values of  at which Equation (6) has two positive solutions. Two positive solutions occur when there exists the collapse of pre-existing two solutions in one, that is, the curve of the function
at which Equation (6) has two positive solutions. Two positive solutions occur when there exists the collapse of pre-existing two solutions in one, that is, the curve of the function  is tangent (intercepts in one point) with the curve of the function
is tangent (intercepts in one point) with the curve of the function . The other positive solution always exists. This behavior occurs at two values of
. The other positive solution always exists. This behavior occurs at two values of , named
, named  and
and , with
, with . At these values we must have
. At these values we must have  and
and , or the algebraic equations
, or the algebraic equations
 (B.1)
(B.1)
are satisfied, where the first equation resulted by isolateing  from Equation (6). Hence,
from Equation (6). Hence, 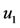 and
and 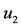 (and corresponding
(and corresponding 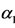 and
and ) are solutions of the second equation substituting
) are solutions of the second equation substituting  from the first equation. From the behaviors of the functions
from the first equation. From the behaviors of the functions  and
and , we can estimate both solutions:
, we can estimate both solutions: 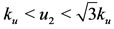 and
and . In the case of three positive solutions, we have the hysteresis behavior [21]. Notice that when
. In the case of three positive solutions, we have the hysteresis behavior [21]. Notice that when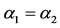 , or when Equation (B.1) does not have solutions, we have exactly one equilibrium value
, or when Equation (B.1) does not have solutions, we have exactly one equilibrium value  for
for .
.
With respect to Equation (8), the function  is strictly decreasing linear function, which intercepts horizontal axis,
is strictly decreasing linear function, which intercepts horizontal axis,  , at
, at .
.
The function  is such that
is such that ,
,  , and
, and
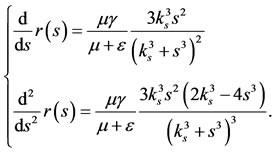
Hence,  is strictly increasing function, and changes the concavity at
is strictly increasing function, and changes the concavity at 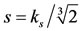 (upward concavity for
(upward concavity for , and downward concavity for
, and downward concavity for ). By comparing the behaviors of the functions
). By comparing the behaviors of the functions  and
and , we conclude that the equation
, we conclude that the equation  has only one positive solution
has only one positive solution , with
, with , for a given positive value of
, for a given positive value of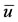 .
.
Notice that, if we consider Hill function of any order for the populational acquisition of the food allergy, that is,  in the last equation of the system (1), a similar conclusion with respect to unicity of the solution can be made. For instance, for
in the last equation of the system (1), a similar conclusion with respect to unicity of the solution can be made. For instance, for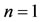 , the equilibrium
, the equilibrium  is the positive solution of
is the positive solution of
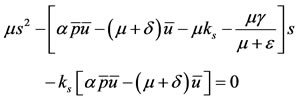
instead of Equation (8). This second order polynomial has one positive solution (other is negative). The qualitative dynamics of the system also does not change. Hence, due to the less sensitive changes in the dynamics promoted by any order of the Hill function, we can revise the model's assumption about the less frequent occurrence of allergic reaction in sensitized persons, if necessary.
Summarizing, the non-trivial equilibrium point  always exists for
always exists for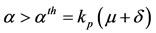 , and is given by
, and is given by
 (B.2)
(B.2)
where 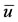 and
and 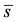 are the positive solutions of, respectively, Equations (6) and (8). We recall that the expressions for
are the positive solutions of, respectively, Equations (6) and (8). We recall that the expressions for  and
and  are given by Equations (5) and (7), respectively. When there are three equilibrium points, for each
are given by Equations (5) and (7), respectively. When there are three equilibrium points, for each ,
, 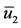 and
and , we calculate other coordinates and we have three equilibrium points
, we calculate other coordinates and we have three equilibrium points ,
,  and
and .
.
1.2. Stability Analysis
The local stability of the equilibrium points is determined by the eigenvalues of the characteristic equation , where the matrix
, where the matrix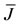 , the Jacobian
, the Jacobian  evaluated at the equilibrium point, is
evaluated at the equilibrium point, is
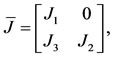
where 0 is the  null matrix, the diagonal matrices are
null matrix, the diagonal matrices are

where
 and
and
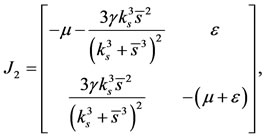
and the off-diagonal matrix is
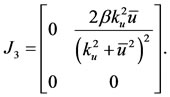
The eigenvalues corresponding to  are the sum of the eigenvalues of the matrices
are the sum of the eigenvalues of the matrices  and
and  [29].
[29].
The characteristic equation corresponding to  is
is
 , (B.3)
, (B.3)
which has positive coefficients. The characteristic equation corresponding to 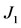 is written as
is written as
 (B.4)
(B.4)
where  and
and  are the trace and determinant of the matrix
are the trace and determinant of the matrix  given by
given by
 (B.5)
(B.5)
We can also evaluate the discriminant of the matrix ,
, . If
. If , the eigenvalues are real. Notice that
, the eigenvalues are real. Notice that
 (B.6)
(B.6)
and the eigenvalues corresponding to the matrix  are negative real numbers.
are negative real numbers.
According to Routh-Hurwitz criteria for a second degree polynomial, if all coefficients are positive, then the characteristic equation has eigenvalues with negative real part [21]. Hence, the characteristic Equation (B.3) has two eigenvalues with negative real part, leaving the stability being determined by the characteristic Equation (B.4). The last term of the trace of ,
,  , was obtained substituting the equilibrium value of
, was obtained substituting the equilibrium value of  given by Equation (5) in
given by Equation (5) in . Taking into account this term, when
. Taking into account this term, when  (and, consequently,
(and, consequently,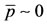 ), the coefficients of the characteristic Equation (B.4) are positive, and both eigenvalues have negative real part. Therefore, the non-trivial equilibrium point
), the coefficients of the characteristic Equation (B.4) are positive, and both eigenvalues have negative real part. Therefore, the non-trivial equilibrium point 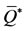 with elevate number of antiacid users is locally asymptotically stable. In other cases, the stability is determined numerically.
with elevate number of antiacid users is locally asymptotically stable. In other cases, the stability is determined numerically.
In the case of the trivial equilibrium point , which has
, which has  and
and , the eigenvalues of the characteristic Equation (B.4) are
, the eigenvalues of the characteristic Equation (B.4) are  and
and . Hence, the trivial equilibrium point is locally asymptotically stable for
. Hence, the trivial equilibrium point is locally asymptotically stable for ; otherwise, unstable. The bifurcation occurs from trivial to non-trivial equilibrium at
; otherwise, unstable. The bifurcation occurs from trivial to non-trivial equilibrium at .
.
If the recruitment of the naive persons is lower than the threshold ( ), the trivial equilibrium point is an attractor disregarding the initial conditions. To prove that the absence of antiacid users is globally stable for
), the trivial equilibrium point is an attractor disregarding the initial conditions. To prove that the absence of antiacid users is globally stable for , let us define Lyapunov function
, let us define Lyapunov function  as
as
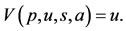
The orbital derivative is
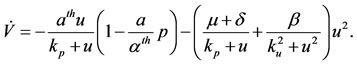
Notice that if , we have
, we have ; also, being
; also, being , we have
, we have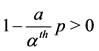 . Hence, the orbital derivative
. Hence, the orbital derivative 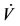 is lower than or equal to zero for
is lower than or equal to zero for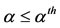 . By inspecting the system of Equation (1), it can be seen that the maximal invariant set contained in
. By inspecting the system of Equation (1), it can be seen that the maximal invariant set contained in  is the trivial equilibrium point. Then, from La-Salle Lyapunov Theorem [30], the equilibrium point
is the trivial equilibrium point. Then, from La-Salle Lyapunov Theorem [30], the equilibrium point  corresponding to the absence of antiacid users is globally asymptotically stable for
corresponding to the absence of antiacid users is globally asymptotically stable for .
.
NOTES