Application of the Todd-Coxeter Algorithm in the Computation of Group Theory

Moumouni Djassibo Woba

Unité de Formation et de Recherhe, Université de Ouahigouya, Ouahigouya, Burkina Faso.

DOI: 10.4236/alamt.2023.133003                

Abstract

In this article, we have described the Todd-Coxeter algorithm. Indeed, the Todd-Coxeter algorithm is a mathematical tool used in the field of group theory. It makes it possible to determine different possible presentations of a group, i.e. different ways of expressing its elements and operations. We have also applied this algorithm to a subgroup generated H by G; where we obtained a table of the subgroup, three tables of relators including: Table of the relator aaaa; Table of the relator abab; Table of the relator bbb and a multiplication table aa'bb'. Once the algorithm is complete, the unit of H in G is 6. We have explicitly obtained a homomorphism of G in the group of permutations of H/G which is isomorphic to G₆; where we have noticed that it is injective: in fact, an element of the nucleus belongs to the intersection of the $xH{x}^{-1}$ for $x\in G$ , in particular, it belongs to H; on the other hand, the image of H in G₆ is of order 4, so the nucleus is reduced to the neutral element.

Keywords

Todd-Coxeter Algorithm, Subgroup, Semi-Direct, Operating Group, Homomorphism

1. Introduction

The concept of a group appeared in the study of polynomial equations. Indeed, it was Evariste Galois who, during the 1830s, used the term “group” for the first time in a technical sense similar to what is used today, making him one of the founders of group theory. As a result of contributions from other fields of mathematics, such as number theory and geometry, the notion of a group was generalized and more firmly established around the 1870s. Modern group theory, a branch of mathematics that is still active, therefore focuses on the structure of abstract groups, regardless of their extra-mathematical use. In doing so, mathematicians have defined, over the years, several notions that allow groups to be fragmented into smaller, more comprehensible objects, subgroups, quotient groups, normal subgroups, and simple groups are some examples. In addition to studying these types of structures, group theorists are also interested in the deferential ways in which a group can be concretely expressed, both from the point of view of representation theory and from the point of view of computationality. Finite group theory was developed with the classification of finite groups as a culmination, which was completed in 2004 [1].

Since the mid-1980s, geometric group theory, which is concerned with finite-type groups as geometric objects, has become a particularly active field in group theory. This article will allow us to “revise” some theoretical notions about groups. We will manipulate permutation groups and groups defined by generators and relationships. It must be said here that other software such as GAP is much more suitable for group theory calculations. However, we will exploit the Todd-Coxeter algorithm for the computation of group theory.

1.1. Distinguished Subgroup, Quotient Group

In the following, G is a group and H is a subgroup of G.

A subset of G modulo H is a subset of G of type $H_g$ (resp ${.}_{g}H$ ) for a $g\in G$ . The set of classes on the right (resp. on the left) is denoted H\G (resp. G\H) and is called the quotient set (on the right, resp. on the left) of G by H. The canonical surjection $G \to H\backslash G$ (resp. G\H) defined by $g\mapsto H_g$ (resp. $g\mapsto {.}_{g}H$ ) is called the canonical projection modulo H on the right (resp. on the left).

1.2. Definition

H is said to be distinguished or normal in G if for all $g\in G$ , we have ${,}_g{H}_{g^{-1}} \subset H$ , or if for all $g\in G$ and for $g\in G$ and for $h\in H{,}_g{h}_{g^{-1}}\in H$ . If H is distinguished, we have $gH = Hg$ and the classes on the right have the same as the classes on the left.

1.3. Theorem

The subgroup H is distinguished in G if and only if there exists a group structure on G/H such that the canonical projection $G\to G\backslash H$ is a group homomorphism. The distribution is then unique and $G/H=H\backslash G$ is called the quotient group [2].

2. Swap Group

We denote ${\mathfrak{G}}_n$ the symmetric group of degree n, i.e. the group of bijections of the set with n elements $\left\{1,\cdots ,n\right\}$ in itself equipped with the law of composition. A permutation of degree n is an element of ${\mathfrak{G}}_n$ . A group of permutations (of degree n) is a subgroup of ${\mathfrak{G}}_n$ . Recall that there is a single homomorphism of ${\mathfrak{G}}_n\to \left\{\pm 1\right\}$ such that the image of a transposition is −1. It’s the signature. The nucleus is the alternating group 𝔘_n.

U_n r-cycle cycle (or r-length cycle) is denoted $\left(a_1{a}_2\cdots a_r\right)$ . This is the permutation that sends $a_1$ to $a_2\cdots a_r$ to $a_1$ . The set $\left(a_1\cdots a_r\right)$ is called the support of the cycle $\left(a_1{a}_2\cdots a_r\right)$ .

Proposition

The group ${\mathfrak{G}}_n$ is generated by (1 2) and (1 2...n). Group ${\mathfrak{U}}_n$ is generated for $n>3$ by (1 2 3) and (3...n) if n is odd and by (1 2 3) and (1 2) (3...n) if n is even.

The first statement is classical. For the second, we recall that ${\mathfrak{U}}_n$ is generated by the 3-cycles (1 2 i) for $i\in \left\{3\cdots n\right\}$ . If $c=\left(1,2,3\right)$ and $\sigma =\left(1,2\right)\left(3\cdots n\right)$ or $\sigma =\left(3\cdots n\right)$ according to the parity of n, we have ${\sigma }_{i}c{\sigma }_{-1}$ = (1 2 3 + i) or (2 1 3 + i) = (1 2 3 + i)². The preceding proposition is easily deduced from this.

3. Group Operating on a Set

Definition

Let X be a set. A group G operating (left) on X is a group with an application $G\times X\to X:\left(g,x\right)\mapsto g\cdot x$ verifying $\left(g{g}^{\prime }\right)\cdot x=g\cdot \left(g^{\prime }x\right)$ for any $g,g^{\prime }\in G$ and $x\in X$ and $e\cdot x=x$ if e is a neutral element of G. It is the same thing to give oneself a homomorphism of groups $G\to S\left(X\right)$ where $S\left(X\right)$ designates the group of permutations of X.

G is said to operate transitively on X if for all x and $y\in X$ , there exists $g\in G$ such that $gx=y$ . It is the same thing to say that the orbit of any $x\in X$ , that is, the set of $g\cdot x$ for $g\in G$ , is equal to X. If G is defined as a group of permutations of degree n and its natural action on $\left\{1,\cdots ,n\right\}$ is transitive, G is said to be transitive.

G is said to operate 2-transitively on X if for all $\left(x,y\right)\in X\times X$ with $x\ne y$ and for $\left(x^{\prime },y^{\prime }\right)\in X\times X$ with $x\ne y$ , there exists $g\in G$ such that g $x=x^{\prime }$ and $gy=y^{\prime }$ . In particular, G operates transitively on X and G operates 2-transitively if and only if the diagonal action of G on $X\times X:g\cdot \left(x,y\right)=\left(g\cdot x,g\cdot y\right)$ has exactly two orbits: the diagonal of $X\times X$ and the complement. A group of permutations of degree n operating 2-transitively on $\left\{1,\cdots ,n\right\}$ is said to be 2-transitive [3].

4. Group Operating on Itself by Conjugation

A group G operates on itself by conjugation: $\left(g,x\right)\mapsto gx{g}^{-1}$ . Two elements a and $b\in G$ are said to be conjugated if there is $g\in G$ such that $b=ga{g}^{-1}$ . The equation to the classes is the formula

$card\left(G\right)={\displaystyle {\sum }_{i}card\left(C_i\right)}$

where C_i goes through all the classes of conjugation. It is easy to calculate the conjugation classes of 𝔊_n. If σ is a permutation, it can be uniquely written as the product of disjointed support cycles.

4.1. Proposition

Two elements of 𝔊_n are conjugated if and only if their decompositions into disjoint cycles have for all i the same number of cycles of length i.

4.2. Group Operating through Translation

A group G operates on itself by translation (left): $\left(g,x\right)\mapsto g\cdot x$ . If H is a subgroup of G, the group G also operates on the set G/H by translations, which allows us to define a homomorphism of ρ groups: $G\to S\left(G/H\right)$ by $\rho \left(g\right)\left(C\right)=gC$ for $g\in G$ and C an element of G/H. In particular, once these Additional definitions: derived subgroup, semi-direct product are numbered from 1 to n if n is the index of H in G, we obtain a homomorphism ρ' of G in 𝔊_n. Note that ${\rho }^{\prime }\left(G\right)$ is a group of transitive permutations of degree n, quotient of G.

5. Additional Definitions: Derived Subgroup, Semi-Direct Product

5.1. Definition

Let G be a group. A commutator is an element d G of the form $xy{x}^{-1}{y}^{-1}$ . We call the derivative group of G (and we denote G' or D(G)) the subgroup generated by the switches of G.

5.2. Proposition

D(G) is a distinguished subgroup of G. The quotient G/D(G) is an abelian group and even the largest abelian quotient group of G in the following sense: let us $\pi :G\to G/D\left(G\right)$ ; if G₁ is an abelian group and $f :G\to G_1$ a homomorphism of groups, there exists a unique homomorphism $\overline{f}:G/D\left(G\right)\to G_1$ such that $\overline{f}\circ \pi =f$ . Thus, the order of G/D(G) is maximal among the order of the quotients of G that are abelian. A sequence derived from a group G is called the sequence $G_0 = G,G_1=D\left(G_0\right),\cdots ,G_k=D\left(G_{k-1}\right),\cdots$

5.3. Theorem

The group derived from 𝔊_n is ${\mathfrak{U}}_n$ . The group derived from ${\mathfrak{U}}_n$ is ${\mathfrak{U}}_n$ for $n\ge 5$ . for $n=4$ , ask MAPLE later for their thoughts [4].

5.4. Definition

Let H and K be two groups and $T:K\to Aut\left(H\right)$ a group homomorphism (here, Auto(H) is the group of bijective homomorphisms of H in itself). The semi-direct (abstract) product of H by K with respect to T is the set $H\times K$ with the following law.

$\left(h,k\right)\ast \left(h^{\prime },k^{\prime }\right)=\left(hT\left(k\right)\left(h^{\prime }\right),k{k}^{\prime }\right).$

This law is a group law, let us denote G group. When T is the trivial homomorphism, we find the direct product. It is easy to show that the sets $H^{\prime }=H\times \left\{1\right\}$ and $K^{\prime }=\left\{1\right\}\times K$ are the subgroups of G, that H' is distinguished in G and that $K^{\prime }\cap H^{\prime }=\left\{1\right\}$ .

5.5. Definition

Let G be a group and let H and K be two subgroups of G. G is said to be the semi-straight product of H by K if H is distinguished in G, if $G=HK$ and if $H\cap G=\left\{1\right\}$ .

Under the previous conditions, let us take $T:K\to Aut\left(H\right)$ gives by $k\mapsto \left(h\mapsto kh{k}^{-1}\right)$ . Then G is isomorphic to the semidirect (abstract) product of H by K with respect to T.

6. Free Groups, Generator-Defined Groups, and Relationships

6.1. Definition

Let V be a set. The free monoid of base V is the set note $V^{*}$ , of finite sequences of elements of V. These sequences are denoted by juxtaposing the elements, for example the sequence $\left({\upsilon }_1,\cdots ,{\upsilon }_r\right)$ with ${\upsilon }_i\in V$ is denoted ${\upsilon }_1,\cdots ,{\upsilon }_r$ . The elements of $V^{*}$ , are called strings of elements of V or words on V.

If $\upsilon ={\upsilon }_1,\cdots ,{\upsilon }_r\in V^{*}$ , with ${\upsilon }_i\in V$ , The length of the string $\upsilon$ is r. We denote ρ the natural map $V\to V^{*}$ which to $\upsilon$ associates the chain of length 1 formed by $\upsilon$ . If ${\upsilon }_1$ and ${\upsilon }_2$ are words, the word formed by juxtaposing them is denoted ${\upsilon }_1{\upsilon }_2$ and is called the concatenation of ${\upsilon }_1$ and of ${\upsilon }_2$ .

6.2. Proposition

The concatenation defines an internal composition law on $V^{*}$ which is associative and admits a neutral element ε which is the empty string.

6.3. Proposition (Universal Property of $V^{\ast }$ )

For any monoid M and any map $f :V\to M$ , there exists a single monoid morphism $f^{*}:V^{*}\to M$ such that $f =f^{*}o\rho$ .

Note that $V^{*}$ is characterized by the preceding universal property with a single isomorphism. Let V' be a copy of V. If $\upsilon$ is an element of V, we denote ${\upsilon }^{\prime }$ the same element seen in V'.

Let $\overline{V}=V\bigsqcup V^{\prime }$ be the disjoint meeting of V and V'. Let ${\overline{V}}^{*}$ be the free monoid of base V'. Si $\alpha ={\alpha }_1\cdots {\alpha }_r$ , we set ${\alpha }^{\prime }={\alpha }_{r^{\prime }}\cdots {\alpha }_{1^{\prime }}$ .

6.4. Definition

Two elements of ${\overline{V}}^{*}$ are said to be equivalent if there are $n\in \mathbb{N}$ and ${\alpha }_0,{\alpha }_1,\cdots ,{\alpha }_n$ belong to ${\overline{V}}^{*}$ such that ${\alpha }_0={\alpha }_1\cdot {\alpha }_n=\beta$ and such that if $0\le i<n$ , ${\alpha }_i$ and ${\alpha }_{i+1}$ are contiguous. The relation thus defined is an equivalence relation. The parity of the length is conserved by this relation.

6.5. Definition

The free group F(V) of base V is the set of equivalence classes of the previous equivalence relation. We check that the concatenation respects the equivalence relation. This makes it possible to define an internal composition law on F(V).

6.6. Proposition

Equipped with the concatenation, F(V) is a group. For $\alpha \in V$ , the inverse of (the class) of $\alpha$ is (The class of) ${\alpha }_0$ . For this reason, ${\alpha }_0={\alpha }^{-1}$ for $\alpha \in V$ is also denoted. We still have a map $\overline{\rho }:V\to F\left(V\right)$ .

6.7. Proposition (Universal Property of F(V))

For any group G and any map $f:V\to G$ , there exists a unique homomorphism of group $\overline{f}:F\left(V\right)\to G$ such that $f=\overline{f}o\rho$. Again, F(V) with the map $\overline{\rho }:V\to F\left(V\right)$ is characterized with a single isomorphism by the universal property above.

6.8. Examples

1) If V is the empty set, the base free group V is the trivial group {1}.

2) If $V=\left\{\alpha \right\}$ is reduced to one element, F(V) is isomorphic to $\mathbb{Z}$ Indeed, we begin to enumerate the elements of F(V) by “reducing” them: these are the α...α (n times ) = αⁿ and the α'...α' (n times) = α'ⁿ = α⁻ⁿ for $n\in \mathbb{N}$ . Notice that $\mathbb{Z}$ verifies the universal property: if G is a group, an application.

$f:\left\{\alpha \right\}\to G$ is determined by the image $b=f\left(\alpha \right)\in G$ ; there is then a single group homomorphism of $\mathbb{Z}$ in G given by $n\to b^n$ . By uniqueness of the universal object, we deduce that F(V) is isomorphic to $\mathbb{Z}$ .

3) If V has two elements α and β, F(V) is very large: it contains, for example αb, αbα, αbα⁻¹b, α⁵b²αbαbαb, etc. which are all distinct.

6.9. Definition

Let be a group and A, a part of G. The distinguished subgroup of G generated by A is the intersection of all the distinguished subgroups of G containing A. It is also the smallest distinguished subgroup of G containing A. It is formed of the finite products of elements of A and all their conjugates by an element of G.

6.10. Definition

A group presentation is a pair (X, R) where X is a set and R is a part of F(X). Let $G=\langle X/R\rangle$ be the quotient of the free group F(X) by the distinguished subgroup of F(X) generated by R. We say that (X, R) is a presentation of G or that it is a definition of G by generators and relations. The elements of X are called generators, the elements of R are called relators. If r is a relator, r = 1 is called a relation. We also denote $\langle X/R\rangle =\langle X|\omega =1\text{for}\omega \in R\rangle$ .

By example

$\langle \mathcal{x},\mathcal{y}|x^2,y^2,\mathcal{x}\mathcal{y}{\mathcal{x}}^{-1}{y}^{-1}\rangle$ or $\langle \mathcal{x},\mathcal{y}|x^2=1,y^2=1,\mathcal{x}\mathcal{y}= \mathcal{y}\mathcal{x}\rangle$ ,

$\langle \mathcal{x},\mathcal{y}|x^n,y^2,\mathcal{y}\mathcal{x}{\mathcal{y}}^{-1}\mathcal{x}\rangle$ or $\langle \mathcal{x},\mathcal{y}|x^n=1,y^2=1,\mathcal{y}\mathcal{x}{\mathcal{y}}^{-1}={\mathcal{x}}^{-1}\rangle$ .

6.11. Proposition (Universal Properties)

For any group G and any map $f:X\to G$ such that $\overline{f}\left(r\right)=1$ for $r\in R$ , there exists a unique homomorphism of group $f^{\prime }:\langle X/R\rangle \to G$ such that $f =f^{\prime }o\pi o\overline{\rho }$ where π is the projection of F(X) onto $\langle X/R\rangle$ .

6.12. Examples

1) If R is the empty set, the subgroup of F(X) generated by R is reduced to 1. So $\langle H/R\rangle =F\left(X\right)$ .

2) $G=\langle a/a^5\rangle$ 〉 is isomorphic to $\mathbb{Z}/5\mathbb{Z}$ . Indeed, we have $F\left(\left\{a\right\}\right)=a^{\mathbb{Z}}$ , the distinguished subgroup generated by $a^5$ is $a^{5\mathbb{Z}}$ .

3) $G=\langle a,b/a^3,b^2,ab{a}^{-1}{b}^{-1}\rangle$ is isomorphic to $\mathbb{Z}/6\mathbb{Z}$ . Indeed, in ${\overline{X}}^{*}$ $ab~ab{a}^{-1}a~ab{a}^{-1}{b}^{-1}ba~ba$ . We enumerate the elements of G: we find 1, $a,a^2,b,ba,b{a}^2$ . So $\left|G\right|\le 6$ . On the other hand, the group $\mathbb{Z}/6\mathbb{Z}$ has two generators x = 2 and y = 3 verifying (additive notation) $\mathcal{x}=0$ , $2\mathcal{y}=0$ , $\mathcal{x}+\mathcal{y}-\mathcal{x}-\mathcal{y}=0$ . We deduce from this by the universal property that there exists a group homomorphism $G\to \mathbb{Z}/6\mathbb{Z}$ which sends a over x = 2 and b over y = 3. It is surjective. Hence $\left|G\right|\ge 6$ . So $\left|G\right|=6$ and G is isomorphic to Z/6Z.

4) Recognize the groups $\langle \mathcal{x}/{\mathcal{x}}^n=1\rangle$ , $\langle \mathcal{x},\mathcal{y}|x^2=1,y^2=1,\mathcal{x}\mathcal{y}=\mathcal{y}\mathcal{x}\rangle$ .

7. Proof and Analysis of the Isomorphism Relationship between G and G₆, in Particular How to Determine the Injectivity of the Maple and Its Specific Shape

Here is a more rigorous analysis of the isomorphism relationship between the graph G and the G₆ graph, including details on the demonstration of the injectivity of the extension of G in G₆ and t the specific form of this extension.

1) Definition of G and G₆

• G is an undirected graph connected to n vertices and m edges.

• G₆ is a connected undirected graph with 6n vertices and 6m edges, constructed from G by replacing each vertex of G with a sextet (group of 6 vertices) and each edge of G with a sextoid (group of 6 edges).

2) Demonstration of the injectivity of the extension of G in G₆

• Let $f:G_n\to G_6$ the embedding that associates to each vertex of G the corresponding sextet in G₆, and to each edge of G the corresponding sextoid in G₆.

• Let us show that f is injective:

• Let u and v be two distinct vertices of G.

• Their corresponding sextons in G₆ are also distinct, as they each contain 6 distinct vertices.

• Similarly, the sextoids corresponding to the edges incident u and v in G are distinct in G₆.

• Therefore f(u) differ f(v), which proves the injectivity of f.

3) Specific shape of the embedding f:

• Let v be a vertex of G, and let $\left(v_1,v_2,v_3,v_4,v_5,v_6\right)$ be the 6 vertices of the sextet correspond in G₆.

• The edges of the sextoid corresponding to an edge $\left(u_0,v_0\right)$ and G are: $\left(u_1,v_1\right)$ ; $\left(u_2,v_2\right)$ ; $\left(u_3,v_3\right)$ ; $\left(u_4,v_4\right)$ ; $\left(u_5,v_5\right)$ ; $\left(u_6,v_6\right)$ .

• Thus, the structure of the G group is preserved in G₆ via this extension.

4) Consequences:

• The embedding f establishes an isomorphism between G and an induced subgraph of G₆.

• This isomorphism makes it possible to transfer the topological and structural properties of the graph G to the isomorphic subgraph of G₆.

• In particular, if G is connected, bipartite, planar, etc., then the isomorphic subgraph of G₆ will have the same properties.

In summary, the demonstration of the injectivity of the f-embedding and the description of its specific forms allow us to characterize the isomorphism relationship between the graphs G and G₆. This opens the way to the in-depth study of the properties of the G₆ graph based on that of the G graph.

8. Familiarization with Group

The group library is concerned with two types of groups: groups of permutations of degree n, which are given by a list of generators and the integer n, and groups defined by generators and relations. It will be noticed right away that some commands can be used for both types of groups, such as cosets and cosrep, which are normal, while others can only be used with a permutation group, such as conjugate, center, centralizer, and subgroup. Finally, some commands are only applicable to a group defined by generators and relations, such as permrep and pres.

The command to define a permutation group is permgroup. It is important to be familiar with the two ways in which MAPLE represents a permutation σ. We can give ourselves a permutation list, i.e. the list $\left[\sigma \left(1\right),\cdots ,\sigma \left(n\right)\right]$ . Thus, [1, 3, 4, 5, 2] denotes for MAPLE the permutation

$\left(\begin{array}{ccc}1& 2& \begin{array}{cc}3& \begin{array}{cc}4& 5\end{array}\end{array}\\ 1& 3& \begin{array}{cc}4& \begin{array}{cc}5& 2\end{array}\end{array}\end{array}\right)$

We can also give ourselves the permutation σ as the list of cycles with disjoint support whose product is σ: [[1, 2, 3], [4, 5]] designates the permutation (123) (45). We go from one to the other by cover ((“permlist”, n) and open (“disjcyc”). We can also give ourselves the permutation σ as the list of cycles with disjoint support whose product is σ: [[1, 2, 3], [4, 5]] designates the permutation (123) (45). We go from one to the other by cover ((“permlist”, n) and open (“disjcyc”).

Example:

> overcast ([1, 3, 4, 5, 2], “disjcyc”);

> Overcast ([[1, 2, 3], [4, 5]], “permlist”, 5);

> overcast ([[1, 2, 3], [4, 5]], “permlist”, 9);

In the second command, the permutation is seen as an element of 𝔊₅, in the third as an element of 𝔊₉. Operations on permutations are given by invperm, mulperms. Check on an example that MAPLE makes the permutations on the right: ${\sigma }_{2}o{\sigma }_1 ={\sigma }_{1}o{\sigma }_2$ , noting $\sigma \left(i\right)=i^{\sigma }$ (exponential notation), we then have $i^{{\sigma }_1\cdot {\sigma }_2}={\left(i^{{\sigma }_1}\right)}^{{\sigma }_2}$ . As a result, MAPLE instead calculates the classes on the right on which G operates on the right. Some commands do not give results when the generators have been named. If this problem is encountered, the following procedure can be used to remove these names:

> gr: = pro(G) local a,b,L,c;

> a=op (1, G); b: = op(2, G);

> L: {};

> for c in b do

> if type (c, ‘=’) then c: =op (2, c) fi;

> L: ={op(L), c};

> od;

> permgroup (a,L);

> end;

9. Conclusions

If a G is a group defined by generators and relations such as: $G=\langle X|R\rangle$ with finite X and H a subgroup of G generated by the image of a finite subset S of words of $\overline{X}=X\bigsqcup X$ .

The Todd-Coxeter algorithm allows, when the index of H in G is finite, to calculate this index and to give the action of G by right translation on the set of classes H\G. The group library concerns two types of groups: groups of permutations of degree n, which are given by a list of generators and the integer n, and groups defined by generators and relationships.

MAPLE calculates the classes on the right on which G operates on the right. Some commands do not give results when the generators have been named. If this problem is encountered, the following procedure can be used to remove these names:

> gr: =pro(G) local a,b,L,c;

> a=op (1, G); b: =op (2, G);

> L: {};

> for c in b do

> if type (c, ‘=’) then c: =op (2, c) fi;

> L: ={op(L), c};

> od;

> permgroup (a,L);

> end;

Appendix

A1. Told-Coxeter Algorithm

The Todd-Coxeter algorithm is best known for solving problems related to group theory, by allowing finite presentations of groups to be calculated. However, this algorithm also has interesting applications in other fields:

1) Combinatorial optimization: The Todd-Coxeter algorithm can be used to solve some combinatorial optimization problems, such as the traveling salesman problem. By modeling the problem in the form of relationships between cities (such as generators and relationships in a group), we can use the algorithm to find optimal solutions.

2) Formal language theory: The algorithm can be applied to the study of formal languages, in particular to compute finite automata equivalent to algebraic grammars. This makes it possible to obtain compact and efficient representations of certain languages.

3) Cryptography: In some cryptographic schemes based on group theory, the Todd-Coxeter algorithm can be used to efficiently manipulate the representations of the groups involved.

4) Algebraic topology: In knot theory, for example, the algorithm can help compute topological invariants by modeling knots as groups of braids.

5) Mathematical physics: Some mathematical models in physics, such as crystal lattices, can be studied using the Todd-Coxeter algorithm to understand their algebraic properties.

6) Computer science theory: the algorithm has links to classical problems of complexity theory, such as the group isomorphism problem.

Although the Todd-Coxeter algorithm is historically associated with group theory, these examples show that it can be useful in many other fields requiring the efficient computation of finite algebraic structures. Its adaptability makes it a powerful tool for solving a wide variety of practical problems.

Let G be a group defined by generators and relations: $G=\langle X|R\rangle$ with finite X and H a subgroup of G generated by the image of a finite subset S of words of $\overline{X}=X\bigsqcup X$ . The Todd-Coxeter algorithm that we are going to describe allows, when the index of H in G is finite, to calculate this index and to give the action of G by right translation on the set of classes H\G.

A2. Description of Algorithm

It is a question of giving all classes a number and only one, class H having for example the number 1 (not to be confused with the neutral element). To do this, we will build a certain number of arrays according to the following rules (we recommend doing the following example at the same time).

I) The key steps and principles of the Todd-Coxeter algorithm, an important algorithm in group theory:

a) Group performances:

The algorithm starts by representing the group using generators. This can be done in the form of a group presentation.

b) Initialization: The algorithm starts with an initial set of side classes, which represent the elements of the group. Often, we start with a single class, corresponding to the neutral element of the group.

c) Relationship Processing: At each step, the algorithm takes a relationship between generators and tries to apply it to existing side classes. This can lead to some side classes being identified as identical, thus reducing the total number of classes.

d) Iterative process: the algorithm proceeds iteratively, successively applying the group’s relationships to the lateral classes, until no new identification is possible.

e) Termination: The algorithm terminates when the application of the relationships no longer results in any new identification of side classes. At this point, the final set of side classes represents the elements of the group.

f) Key Principles:

• Relationship Matching: The algorithm seeks to match the group's relationships to existing side classes.

• Merging identical classes: When two side classes are identified as identical, they are merged into a single class.

• Propagation of identifications: the identifications made are propagated through all the lateral classes to ensure consistency.

• Finding a steady state: the algorithm aims to reach a steady state where no new identification is possible.

NB. The Todd-Coxeter algorithm is very useful for studying group structure and calculating invariants such as group order. It has many applications in group theory, algebraic topology, and other mathematical fields.

1) For each word $\alpha =a_{i1}\cdots a_{ir}$ of S, we associate a table M_gen(α) with a single row and r + 1 columns whose first element is 1. We will fill in the second column later by putting the number of the class of $H_{a_{i1}}$ which we also note 1. $a_{i1}$ , then the third column with the number of 1. $a_{i1}\cdot a_{i2}$ , etc.

First principle: The last element in the line is 1. Indeed, if $\alpha \in S$ , we have $H\alpha =H$ . These tables are called the tables of subgroup H. The tables are presented here in the initial state:

2) At each relator $\beta =b_{j1}\cdots b_{\mathcal{j}s}$ , element of R, we associate a M_rel(β) table with s + 1 columns and an unlimited number of rows.

In the first column, we will successively put the numbers introduced 1, 2, 3, ..., class numbers. Again, on the same line, we go from column k to column k + 1 by “multiplication on the right” by $b_{jk}$ .

Second principle: On the same line, the first element and the last element are identical. Indeed, if $\beta \in R$ , $\left(H\mathcal{x}\right)\beta =H\mathcal{x}$ for all $\mathcal{x}\in G$ . This table is called the relator table β.

3) Finally, we construct a table of a different type, similar to a group distribution table (called a multiplication table). The rows are indexed by the numbers of the classes obtained, the columns by the elements of X and their inverses. In place (i, g) is the number of i. g.

4) We build the paintings little by little. As soon as a new number is defined, a row is added to the tables of the relators and the multiplication table. As soon as we give a number to a class, we carry it everywhere we can. If $k = j\cdot x$ , we deduce that $j=k\cdot {\mathcal{x}}^{\prime }$ . If principles 1 and 2 allow deductions to be made, they are used. If we come across a coincidence, for example if a class has both the number 3 and 6, we replace the number 6 with the number 3 everywhere. Once all possible deductions have been made, and if there is an empty box left in the multiplication table, a new number is assigned to an empty box in this table. Otherwise, the algorithm is complete [5].

II) Explanations of the table and how the Todd-Coxeter algorithm helps to understand the structure of subgroups, in particular the role of the relative table and the multiplication table.

The Todd-Coxeter table is a powerful tool for studying the algebraic structure of a group. It allows group relationships to be presented in a compact way in a table format, which facilitates the analysis of subgroups.

The key to the Todd-Coxeter table is the relative table. This table represents the relationships between the items in the group, indicating how each item combines with the generators in the group. Each box in the relative table contains a group item, which is the result of multiplying a row item (representing an item in the group) by a column item (representing a generator).

The Todd-Coxeter algorithm uses this relative table to systematically explore all the elements of the group and identify its subgroups. It proceeds as follows:

1) We start with a set of generators of the group and their relationships.

2) The relative table is constructed by filling each cell with the result of multiplying a row item by a column item, according to the relationships of the group.

3) The algorithm explores the relative table in a systematic way, identifying the items in the group and inferring the subgroup structure.

The multiplication table is another key tool. It is deducted from the relative table and represents the products of all the items in the group. Each box contains the result of multiplying the row item by the column item.

Analysis of the multiplication table makes it possible to identify the subgroups of the initial group. Indeed, the subgroups correspond to blocks of closed squares in the multiplication table, i.e. areas where the multiplications remain inside.

In summary, the Todd-Coxeter table, through its relative table and its multiplication table, offers a compact and powerful representation of the algebraic structure of a group. The Todd-Coxeter algorithm exploits this representation to systematically explore subgroups, which is essential for understanding the overall structure of the group.

A3. Application of the Todd-Coxeter Algorithm

Let’s take $G=\langle a,b|a^4={\left(ab\right)}^2=b^3=1\rangle$ .

So we have $X=\left\{a,b\right\}$ , $R=\left\{aaa,abab,bbb\right\}$

Let us take for H the subgroup generated by a. So there is a subgroup table, three relator tables and a multiplication table [6].

At first, they are of the following form:

Subgroup table:

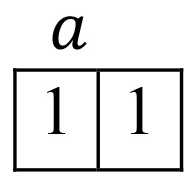
Narrator’s table aaaaa:

Narrator’s table abab:

Narrator’s table bbb:

“Multiplication” table:

The subgroup table will no longer move. We will not rewrite it again.

We take 2 = 1.b. Tables become.

We take 3 = 2.a. Tables become.

We found in passing that 3.b = 1 and 2.b = 3.

We then take 4 = 3.a. Tables become.

We take 5 = 4.a. Tables become.

By the way, we made deductions 5.a = 2 and 4.b = 5.

Finally, we hang 6 = 5.b. Tables become.

The algorithm is finished. The index of H in G is 6. Let’s show that a is of order 4 in G. Since a⁴ = 1, it is of order dividing 4.

Notice that the image of a in S(H\G) is the cycle (2 3 4 5) which is of order 4. Thus, a is of order 4 and G is of order 24. Similarly, the image of b is the permutation (1 2 3) (4 5 6) which is of order 3 [7].

We have explicitly obtained a homomorphism of G in the group of permutations of H\G which is isomorphic to 𝔊₆. Note that it is injective: in fact, an element of the nucleus belongs to the intersection of $\mathcal{x}H{\mathcal{x}}^{-1}$ for $\mathcal{x}\in G$ , in particular, it belongs to H; on the other hand, the image of H in 𝔊₆ is of order 4, so the nucleus is reduced to the neutral element.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Ramis, E. (2005) Classification des finis. Mathematics Reviens, C, 1232.
[2]	Artin, M. (1991) Algebra. Prentice Halloween, 231.
[3]	Quant au nom de l’auteur de l’article.
[4]	Bouvier, A. and Richard, D. (1974) Groupe, Actualités scientifiques et industrielles. Hermann, 543.
[5]	Cameron, P.J. (1999) Permutation Groups, London Math. Soc. Student Texts 45. Cambridge University Press, 876.
[6]	Mazet, P. (1996) Algèbre et géométrie pour le capes et l’agrégation, Ellipses, 321.
[7]	Dixon, J.D. and Mortimer, B. (1996) Permutation Groups, GTM 163. Springer, 943.
[8]	Perrin, D. (1996) Cours d’algèbre. Ellipses, 3452.