The Distribution of Prime Numbers and Finding the Factor of Composite Numbers without Searching

Dagnachew Jenber^*

School of Interdisciplinary Program, Mathematics Division, Addis Ababa Science and Technology University, Addis Ababa, Ethiopia.

DOI: 10.4236/apm.2015.56033                

Abstract

In this paper, there are 5 sections of tables represented by 5 linear sequence functions. There are two one-variable sequence functions that they are able to represent all prime numbers. The first one helps the last one to produce another three two-variable linear sequence functions. With the help of these three two-variable sequence functions, the last one, one-variable sequence function, is able to set apart all prime numbers from composite numbers. The formula shows that there are infinitely many prime numbers by applying limit to infinity. The three two-variable sequence functions help us to find the factor of all composite numbers.

Keywords

The n^th Sequence of an Arithmetic Sequence, Number of Elements of the Set, Sequence Functions

1. Introduction

A prime number (or a prime) is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example, 5 is prime because 1 and 5 are its only positive integer factors, whereas 6 is composite because it has the divisors 2 and 3 in addition to 1 and 6. The fundamental theorem of arithmetic establishes the central role of primes in number theory: any integer greater than 1 can be expressed as a product of primes that is unique up to ordering. The uniqueness in this theorem requires excluding 1 as a prime because one can include arbitrarily many instances of 1 in any factorization, e.g., 3, 1 × 3, 1 × 1 × 3, etc. are all valid factorizations of 3. The property of being prime (or not) is called primality. A simple but slow method of verifying the primality of a given number n is known as trial division. It consists of testing whether n is a multiple of any integer between 2 and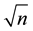. Algorithms much more efficient than trial division have been devised to test the primality of large numbers. Particularly fast methods are available for numbers of special forms, such as Mersenne numbers. As of April 2014, the largest known prime number has 17,425,170 decimal digits. There are infinitely many primes, as demonstrated by Euclid around 300 BC. There is no known useful formula that sets apart all of the prime numbers from composites. However, the distribution of primes, that is to say, the statistical behaviour of primes in the large, can be modelled. The first result in that direction is the prime number theorem, proven at the end of the 19th century, which says that the probability that a given, randomly chosen number n is prime is inversely proportional to its number of digits, or to the logarithm of n. Many questions regarding prime numbers remain open, such as Goldbach’s conjecture (that every even integer greater than 2 can be expressed as the sum of two primes), and the twin prime conjecture (that there are infinitely many pairs of primes whose difference is 2). Such questions spurred the development of various branches of number theory, focusing on analytic or algebraic aspects of numbers. Primes are used in several routines in information technology, such as public-key cryptography, which makes use of properties such as the difficulty of factoring large numbers into their prime factors. Prime numbers give rise to various generalizations in other mathematical domains, mainly algebra, such as prime elements and prime ideals [1] .

In this paper I am going to prove that:

1) 1 is prime number, so the definition of prime number becomes “A prime number (or a prime) is a natural number greater than or equal to 1 that has no positive divisors other than 1 and itself.”

2) There is useful formula that sets apart all of the prime numbers from composites or the distribution of primes.

3) Goldbach’s conjecture and the twin prime conjecture.

4) Finding the factor of any odd composite numbers without searching.

For example to find the factor of composite number

n = 114381625757888867669235779976146612010218296721242362562561842935706935245733897830597 123563958705058989075147599290026879543541 [2] the only thing we need to have is microsoft Excel soft-

ware with big cell and a little bit big screen computer and track the number from the two tables using

two functions that we will discuss. My paper is important to find the factor composite numbers and prime numbers as we want as fast as possible and faster than trial division and algorithmic methods and perfect.

2. Preliminary

Definition (When Is a Number Divisible by 3) [3] .

If the sum of the digits of a number is divisible by 3 , then the original number is divisible by 3.

Definition (When Is a Number Divisible by 5) [3] .

If the last digit of the number being inspected for divisibility is either a 0 or 5, then the number itself will be divisible by 5.

Definition (When Is a Number Divisible by 7) [3] .

Delete the last digit from the given number and then subtract twice this deleted digit from the remaining number. If the result is divisible by 7, the original number is divisible by 7. This process may be repeated if the result is too large for simple inspection of divisibility of 7.

Definition (The 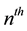term of Arithmetic sequence).

The 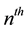term of an Arithmetic sequence is given by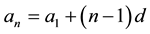, where 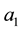is the first term of the sequence and d is the common difference of the sequence.

Definition (Multivariable sequence function).

A function 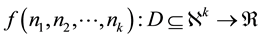is a real valued multi-variable sequence function defined on the set of natural numbers, 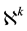, where 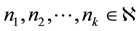and number of elements in the range

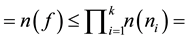the product of number of elements of

Example: If for

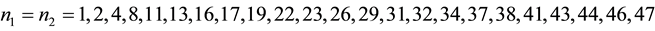, that is, 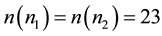, then

number of elements of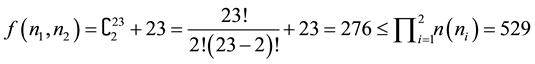, here I take combination

because addition is commutative from the term there- fore order is not considered.

But if, then the number of elements of

, here I take permutation because sub-

traction is not commutative from the term therefore order is considered.

3. Tables

Theorem 1. The linear sequence function represents all odd numbers from 1 to 103 for, where.

Proof. The sequence function is an arithmetic sequence function of decreasing odd numbers from 103 to 1 with common difference 2 and initial term 103, that is, □

Theorem 2. The linear sequence function represents all odd numbers greater than 105 for natural number

Proof. The function is an arithmetic sequence function that represents all odd numbers greater than 105 with common difference 2 and initial term 107, that is □

Theorem 3. The linear sequence function represents all odd numbers greater than 105 except a number which are multiples of 3, 5 and 7 for natural numbers p and n suchthat and 7n.

Proof. Since, then and 7n for all p and n suchthat and 7n. □

Theorem 4. The linear sequence function represents all prime numbers from 1 to 103 except 2, 5 and 7 for natural numbers p and n suchthat and 7n, and, that is, 1 is prime number.

Proof. See Table 1. □

Table 1. My magical table.

Theorem 5. The sequence function represents 1128 different natural numbers for natural numbers and.

Proof. From combination of objects and we have since.

Thus represents 1128 different natural numbers. □

Theorem 6. If, then is composite numbers with factors and, where and are stated from above Theorem-5.

Proof. Since , then is composite numbers with factors and. □

Theorem 7. The sequence function represents 276 different natural numbers which are not multiples of 3, 5 and 7 for natural numbers and n suchthat and 7n and.

Proof. Since, that is, , then

See the following table, where represents the column and represents the row. □

Example: For Theorem 7 see the following Table 2, Table 3 which represents for where represents the first column and represents the first row.

Table 2. Tabular proof for theorem 7.

Table 3. Tabular proof for theorem 7 continued.

Theorem 8. If the sequence function, , then the sequence function represents composite numbers with factors and, where, ,.

Proof. Since, then is composite numbers with factors and for and. □

Theorem 9. If the sequence function, and 7n, where, then the sequence function represents composite numbers which are not multiples of 3, 5 and 7 with factors and, where, , and where.

Proof. If and 7n then and 7n this implies that and 7n.

Thus and 7n this implies that

and 7n for and 7n and composite numbers with factors and.

Example: For Theorem 9 see the following Table 4, Table 5 which represents for where represents the first column and represents the first row.

Table 4. Examples for theorem 9.

Table 5. Examples for theorem 9 continued.

Theorem 10. If the sequence function, , then the sequence function represents composite numbers with factors and, where,.

Proof. Since this implies that is composite numbers with factors and for. □

Theorem 11. If the sequence function, and 7n, where, then the sequence function represents composite numbers which are not multiples of 3, 5 and 7 with factors and, where, and where.

Proof. If and 7n then and 7n this implies and 7n.

Thus and 7n this implies that

and 7n for and 7n and is composite numbers with factors and. □

Example: For Theorem 11 see the following Tables 6-8 which represents for where represents the first column and represents the first row.

Table 6. Examples for theorem 11.

Table 7. Examples for Theorem 11 continued.

Table 8. Examples for Theorem 11 continued.

Theorem 12. The union of three sequence functions, , , , , and , represents the set of natural numbers.

Proof. Let and be disjoint subsets of the set of natural numbers whose union is equal to the set of natural numbers, then there exists and such that

this implies that for

this implies that for

this implies that for

Therefore.

Theorem 13. If then the sequence functions, and represents all odd composite numbers greater than 107, where, , , and, are defined from above Theorem-12.

Proof. Since for

or for

or for and from the above Theorem-12 we have, then represents the set of all odd composite numbers. □

Theorem 14. The sequence function, , represents all prime numbers greater than or equal to 107 for and where, for, for, and for.

Proof. Suppose represents all prime numbers for and 7n.

But or or or or or represents all odd composite numbers then this contradicts our supposition.

Therefore, there exists a number and 7n suchthat represents all prime numbers. □

Theorem 15. There are infinitely many prime numbers.

Proof. Since, then there are infinitely many prime numbers. □

Theorem 16. (Goldbach’s theorem)

Every even integer greater than or equal to 2 can be expressed as the sum of two primes.

Proof. Suppose for, for, and for.

for, for, and for

Thus for all and 7n for there always exists or or such that

or or this implies that

or or (1)

Or for all and 7n for and and for there always exists or or such that

or or this implies that

or or (2)

Or for all and for there always exists or or such that

or or this implies that

or or (3)

Therefore from Equations (1), (2), and (3) we have

or or for, where and

Thus every even integer greater than or equal to 2 can be expressed as the sum of two primes. □

Theorem 17. (Twin prime theorem)

There are infinitely many pairs of primes whose difference is 2.

Proof. Suppose there are infinitely many numbers, and such that, where for, for, , and for,.

Thus and represents prime numbers and and. □

Theorem 18. Suppose, , , , , , , where

are multiples of and 105 respectively and

for,

for,

and for.

If, is the given term prime number, then n can be calculated as:

, where are the first term of which is less than p and number of elements of less than p, number of elements of less than p and number of elements of less than p.

Proof. Since is prime number for and and.

Now let and be in the set of natural numbers such that

where is the first term less than p, this implies that. Thus we have number of terms which are multiples of 3.

where is the first term less than p, this implies that. Thus we have number of terms which are multiples of 5.

where is the first term less than p, this implies that. Thus we have number terms which are multiples of 7.

where is the first term less than p, this implies that. Thus we have number of terms which are multiples of 15.

where is the first term less than p, this implies that. Thus we have number of terms which are multiples of 21.

where is the first term less than p, this implies that. Thus we have number of terms which are multiples of 35.

where is the first term less than p, this implies that. Thus we have number of terms which are multiples of 105.

Thus we have to eliminate number of terms between 1 and p to find the term of prime numbers.

Therefore we have number of prime numbers between 1 and p including 107 and.

Since we have 24 number of prime numbers less than 107, hence

, that is, the prime number is

. □

Example: For Theorem 12 - 18 see the following Tables 9-16. Where the bold face numbers are elements of for, for and, and for. and for.

Table 9. Examples for theorem 12 - 18.

Table 10. Examples for theorem 12 - 18 continued.

Table 11. Examples for theorem 12 - 18 continued.

Table 12. Examples for theorem 12 - 18 continued.

Table 13. Examples for theorem 12 - 18 continued.

Table 14. Examples for theorem 12 - 18 continued.

Table 15. Examples for theorem 12 - 18 continued.

Table 16. Examples for theorem 12 - 18 continued.

Acknowledgements

I thank the editors and the referee for their comments and thanks to my brothers, colleagues and friends: Adem Gulma, Dereje Wasihun, Natnael Nigussie, Ketsela Hailu, Yadeta Chimdessa, Solomon Tesfaye and Abebe Tamrat for thier encouragement and advice next to God and my family.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	(2015) http://en.wikipedia.org/wiki/Prime_number
[2]	Posametier, A.S. (2003) Math Wonders to inspire Teachers and Students.
[3]	Crandall, R. and Pomerance, C.B. (2005) Prime numbers: A Computational Perspective. 21.