Construction and Weight Distributions of Binary Linear Codes Based on Deep Holes

Yong Yang, Wenwei Qiu

School of Mathematics and Information, China West Normal University, Nanchong, China.

DOI: 10.4236/am.2023.1410040                

Abstract

Deep holes are very important in the decoding of generalized RS codes, and deep holes of RS codes have been widely studied, but there are few works on constructing general linear codes based on deep holes. Therefore, we consider constructing binary linear codes by combining deep holes with binary BCH codes. In this article, we consider the 2-error-correcting binary primitive BCH codes and the extended codes to construct new binary linear codes by combining them with deep holes, respectively. Furthermore, three classes of binary linear codes are constructed, and then we determine the parameters and the weight distributions of these new binary linear codes.

Keywords

Linear Codes, MacWilliams Equations, Weight Distribution, Dual Codes, Deep Holes, Covering Radius

1. Introduction

Let 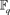be the finite field with q elements, where q is an odd prime. An 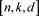linear code is a k-dimensional subspace of the vector space 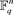with minimum distance d, where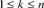. The weight of code x is denoted by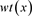. The dual code of, denoted by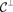, is defined by

Clearly,.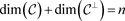

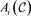For the linear code with length n, the number of codewords of weight i denotes with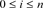. The weight enumerator of is defined by

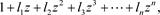
and the sequence 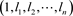is said to be the weight distribution of. If the number of non-zeros in the sequence is t, then we say that the linear code is a t-weight code. The weight distributions of linear codes not only give the important information of linear codes in practice and theory, but also reflect the error-correcting ability of linear codes and the probability of error information occurring during transmission. In general, it is not effortless to determine the weight distributions of linear codes.

The coset of, denoted by Q, is defined by

where is a vector fixed for the given representation. The weight of Q is the smallest Hamming weight of the codewords of Q.

For any vector (codeword), the error distance to code of a received codeword u is defined by

where the minimum Hamming distance between vectors u and c is defined to be

The maximum error distance is defined by

where is called the covering radius of the linear code. If the error distance to code of a received word reaches the covering radius of linear code, the vector u is called the deep hole.

Deep holes have been widely studied in RS codes, and the deep holes of standard RS codes are given in [1] . In addition, Zhang et al. also gave deep holes for several classes of special codes in [2] [3] [4] . Therefore, most scholars are keen on studying the deep holes of some special codes. However, there is little work on constructing general linear codes from deep holes. Thus, we further consider the use of deep holes to construct some binary linear codes.

Around the 1960s, BCH codes were proposed by Hocquenghem [5] and Bose and Ray-Chaudhuri [6] , and the error-correcting codes were studied by Gorenstein and Zierler [7] over finite fields. In 1960, Gorenstein et al. [8] showed that the covering radius of binary 2-error-correcting BCH codes was 3, and further, the covering radius of the extended codes was 4. The study of 2-error-correcting BCH codes is very thorough, including covering radius, weight distribution, coset weight distribution and so on. The covering radius of the 2-error-correcting binary primitive BCH codes is known. From the definition of deep holes, we know that the deep holes of these BCH codes exist. Since linear codes play an important role in the fields of data storage, information security and secret sharing, the construction of linear codes is one of the important contents in the current cryptography and coding research. Therefore, it is very meaningful to construct binary linear codes.

In this paper, our main work is to construct some binary linear codes by combining deep holes with BCH codes. Furthermore, we can determine the parameters and the weight distributions of the binary linear codes. Finally, some examples are presented by Magma experiments, which support the weight distributions of these binary linear codes. These experimental results coincide with the theoretical results.

The rest of this paper is outlined as follows. Section 2 states some notations and results about narrow-sense binary primitive BCH codes and linear codes. In Section 3, three classes of binary linear codes are constructed and their parameters are determined. In Section 4, the weight distributions of these binary linear codes are obtained. Finally, the conclusion of this paper is given.

2. Preliminaries

In this section, we state some basic facts and known results about linear codes and narrow-sense binary primitive BCH codes.

2.1. The Weight Distributions of the Linear Code and Its Dual Code

For an linear code over, and denote its dual by. The weight distribution of can be uniquely determined by the weight distribution of and vice versa. This linear relationship is crucial for investigating and calculating weight distribution, and we call it the MacWilliams identity.

Let and be the number of codewords of weight j in and, respectively. The MacWilliams identity is defined by

(1)

Equivalently, we have

(2)

and it is more convenient for us to calculate. But it involves the Stirling numbers of the second kind, where is defined by

(3)

In particular, if and.

In binary codes, from (2), we deduce

(4)

From (2), the first four Pless power moments are listed as follows ( [9] , p. 259):

2.2. Cyclic Codes and Narrow-Sense BCH Codes

An linear code over the finite field, it is said to be cyclic if the codeword implies. For each vector, define, any code corresponds to a subset of quotient ring. Note that a linear code is cyclic if and only if the corresponding subset is an ideal of the quotient ring. Besides, every ideal of is principal. Thus, every code can be expressed as, where is monic and has the smallest degree. is said the generator polynomial, and is referred to as the check polynomial of.

Let, where m is an integer with. Let be a primitive element of. In addition, let be the minimal polynomial of with over. For any, define

where denotes the least common multiple of these minimal polynomials.

Let denote the cyclic code with generator polynomial, then we know. The set is described as a narrow-sense primitive BCH code with design distance. An linear code is said e-error-correcting if.

Let E denote the 2-error-correcting binary primitive BCH codes, and denote its dual by. The code E is an linear code, for. The code E has parity-check matrix defined by

The code E consists of all binary codewords such that. The extended code of B denote and denote its duals by. A vector r of is where. The code has parameters for. The parity-check matrix is defined by

where is an element of order in. The code consists of all binary codewords such that.

2.3. The Weight Distributions of 2-Error-Correcting Binary Primitive BCH Codes and the Extended Codes

In this subsection, we introduce the weight distributions of the 2-error-correcting binary narrow-sense BCH codes and of their extensions, whose length are respectively and.

The code is an linear code in [10] , for odd. The code is a binary linear code with the weight distribution in Table 1.

The code is an linear code in ( [11] , Table 16.5), for odd. The code is a binary linear code with the weight distribution in Table 2.

The code is an linear code, for even. The code is a binary linear code with the weight distribution in Table 3.

Lemma 1. ( [9] , Lemma 7.5.1) Let be an linear code over. Suppose u is a vector in but not in. The linear code is generated by and u, which is an linear code. Let D be this linear code, then we have

Table 1. The weight distribution of, for odd.

Table 2. The weight distribution of, for odd.

Table 3. The weight distribution of, for even.

In binary codes, it is clear that we have

In other words, we have

Theorem 2. ( [9] , Th. 7.3.1) Let T be a set with. The weight distribution of and are determined by and the with.

It is very convenient for us to calculate the weight distribution. The following corollary can be deduced from Theorem 2.

Corollary 3. Let be an linear code over, and denote its dual by. Then the dual code is a linear code of length n and dimension. Let T be a set with and, so the weight distribution of is uniquely determined. If, (4) is equivalent to

(5)

It is very convenient to calculate the weight distribution of the dual code. If, we use (4).

Theorem 4. ( [9] , Th. 1.4.5) Let be an linear code over, then we have

•.

•, and.

• If is a binary code, which contains the codeword. We know for.

Thus, for a 2-ary linear code, if contains the codeword, then the weight distribution of is symmetric.

3. The Parameters of Three Classes of Binary Linear Codes

In this chapter, we construct three classes of binary linear codes based on deep holes, then determine the parameters of these binary linear codes.

Let be an linear code over the finite field, let u be a deep hole of the linear code, then we construct general linear code. We consider binary BCH codes combined with deep holes to construct general linear codes.

Three classes of binary linear codes are constructed by deep holes combined with the 2-error-correcting binary primitive BCH code and their extended codes, respectively.

Lemma 5. The code E is an linear code. Suppose u is a deep hole of the code E, and construct general binary linear code. Then the code is an linear code, and the dual code is an linear code, where m is odd and.

Proof. Let be a basis for a -dimensional subspace of, and the code E is a vector space. Since the covering radius of code E is 3, from the definition of deep hole, the maximum error distance. Moreover, the minimum distance of E is 5, it is easy to know that. The binary linear code is constructed, we have

Furthermore, we obtain

so the minimum distance of the linear code is 3. The binary code is the vector space. Since, so the dimension of the linear code is. Namely, the code has parameters.

Let set for. As, we get

and. We denote the minimum Hamming distance of the code by, from the weight distribution in Table 1, we have

Then the dual code has parameters, for odd. Therefore, the parameters of the code and of its dual code are determined separately.

We similarly construct several classes of binary linear codes and determine their parameters. The proof is similar to that of Lemma 5 and is omitted here. These binary linear codes are as follows.

Lemma 6. The code is an linear code. Suppose u is a deep hole of the code. We construct general binary linear code. Then the code is an linear code, and the dual code is an linear code, where m is odd and.

Lemma 7. The code is an linear code, suppose is a deep hole of the code. We construct general binary linear code. Then the code has parameters, and the dual code has parameters, for even.

4. The Weight Distributions of Three Classes of Binary Linear Codes

In this part, we determine the weight distributions of these binary linear codes. From the general linear code, the weight distributions of these binary linear codes are related to the coset weight distributions of BCH codes. The coset weight distributions of BCH codes have been studied in the literature [12] [13] .

To facilitate the computation of the weight distribution of the dual code, the following lemma can be deduced.

Lemma 8. Let be an linear code, and denote its dual by. Then and. Thus by Corollary 3, the weight distribution of can be determined by the first d Pless power moments, we obtain

(6)

where is the number of codewords of weight i in.

Theorem 9. The binary code is an linear code, and the dual code is an linear code, where m is odd and. Moreover, the weight distribution of is shown in Table 4.

Proof. Let, as, we have if and. From Table 1, it is easily seen that the minimum weight distribution of is at least 3. Thus, there are three nonzero weights of as follows:

So the weight of the code contains. Let be the total number of codewords with weight in. In addition, let and, where. For binary linear codes, then the first three Pless power moments from Lemma 8, we obtain

(7)

where and.

By solving this system of equations, we obtain the results in Table 4. The proof is complete.

Two examples are presented by Magma experiments, which support Theorem 9.

Table 4. The weight distribution of, for odd.

Example 1. Let and let the deep hole vector, the binary code has parameters. In Theorem 9, the code is a binary linear code with the weight enumerator.

Example 2. Let and let the deep hole vector, the binary linear code has parameters. In Theorem 9, the code is a binary linear code with the weight enumerator.

Theorem 10. The binary code is an linear code, and the dual code is an linear code, where m is odd and. Moreover, the weight distribution of is shown in Table 5.

Proof. Let, as, we have if and. From Table 2, it is easily seen that the minimum weight distribution of is at least 4. Therefore, we know that the code has the following four nonzero weights:

The weight of the code contains. Let be the total number of codewords with Hamming weight in, and let and for. Since is even and contains the codeword. From Theorem 4, we have and for. For the binary linear code, then the first and the third Pless power moments from Lemma 8, we obtain

(8)

where and.

By solving this system of equations, we obtain the results in Table 5. The proof is complete.

Two examples are presented by Magma experiments, which support Theorem 10.

Example 3. Let and let the deep hole vector, the binary linear code has parameters. In Theorem 10, the code is a binary linear code with the weight enumerator.

Table 5. The weight distribution of, for odd.

Example 4 Let and let the deep hole vector, the binary linear code has parameters. In Theorem 10, the code is a binary linear code with the weight enumerator.

Theorem 11. The binary code is an linear code, and the dual code is an, where m is even and. Moreover, the weight distribution of is shown in Table 6.

Proof. Let, as, we have if and. From Table 3, it is easily seen that the minimum weight distribution of is at least 6. Thus, there are six nonzero weights of as follows:

The weight of the code contains. Let be the total number of codewords with Hamming weight in, and let and for. Since is even and contains the code word. From theorem 4, we know that and for. For this binary linear code, then the first, the third and the fifth Pless power moments from Lemma 8 and Corollary 3, we obtain

(9)

where and. Since has parameters, the minimum Hamming distance is 4, so. We need to determine the number of codewords of weight 4 in. Since is a vector in but not in. From Lemma 1, we have

The minimum distance of is 6, thus we have, so

The number of codewords of weight 4 in the coset is determined in the literature ( [13] , Remark 4), then we obtain

Table 6. The weight distribution of, for even.

Thus, we have

By solving this system of equations, we obtain the results in Table 6. The proof is complete.

Two examples are presented by Magma experiments, which support Theorem 11.

Example 5. Let and let the deep hole vector, the binary linear code has parameters. In Theorem 11, the code is a binary linear code with the weight enumerator.

Example 6. Let and let the deep hole vector, the binary linear code has parameters. In Theorem 11, the code is a binary linear code with the weight enumerator.

5. Concluding Remarks

In this paper, we consider binary 2-error-correcting BCH codes combined with deep holes to construct general linear codes, where u is a deep hole of the codes. Therefore, we not only construct three classes of binary linear codes, but also determine the parameters and the weight distributions of these binary linear codes. Furthermore, we wish to construct more general linear codes related to deep holes.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Wu, R.J. and Hong, S.F. (2012) On Deep Holes of Standard Reed-Solomon Codes. Science China Mathematics, 55, 2447-2455. https://doi.org/10.1007/s11425-012-4499-3
[2]	Zhang, J., Fu, F.W. and Liao, Q.Y. (2013) Deep Holes of Generalized Reed-Solomon Codes. Scientia Sinica Mathematica, 43, 727-740. (In Chinese) https://doi.org/10.1360/012012-30
[3]	Zhang, J., Wan, D.Q. and Kaipa, K. (2019) Deep Holes of Projective Reed-Solomon Codes. IEEE Transactions on Information Theory, 66, 2392-2401. https://doi.org/10.1109/TIT.2019.2940962
[4]	Zhang, J. and Wan, D.Q. (2023) On Deep Holes of Elliptic Curve Codes. IEEE Transactions on Information Theory, 69, 4498-4506. https://doi.org/10.1109/TIT.2023.3257320
[5]	Hocquenghem, A. (1959) Codes correcteurs d’rreurs. Chiffres (Paris), 2, 147-156.
[6]	Bose, R.C. and Ray-Chaudhuri, D.K. (1960) On a Class of Error Correcting Binary Group Codes. Information and Control, 3, 68-79. https://doi.org/10.1016/S0019-9958(60)90287-4
[7]	Gorenstein, D. and Zierler, N. (1961) A Class of Error-Correcting Codes in pm Symbols. Journal of the Society for Industrial and Applied Mathematics, 9, 207-214. https://doi.org/10.1137/0109020
[8]	Gorenstein, D., Peterson, W.W. and Zierler, N. (1960) Two-Error Correcting Bose-Chaudhuri Codes Are Quasi-Perfect. Information and Control, 3, 291-294. https://doi.org/10.1016/S0019-9958(60)90877-9
[9]	Huffman, W.C. and Pless, V. (2003) Fundamentals of Error-Correcting Codes. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511807077
[10]	MacWilliams, F.J. and Sloane, N.J.A. (1977) The Theory of Error-Correcting Codes (I and II). North-Holland Publishing Company, Amsterdam.
[11]	Berlekamp, E.R. (1968) Algebraic Coding Theory. McGraw-Hill, New York.
[12]	Assmus, E. and Mattson, H. (1978) The Weight-Distribution of a Coset of a Linear Code (Corresp.). IEEE Transactions on Information Theory, 24, 497-497. https://doi.org/10.1109/TIT.1978.1055903
[13]	Charpin, P. (1994) Weight Distributions of Cosets of Two-Error-Correcting Binary BCH Codes, Extended or Not. IEEE Transactions on Information Theory, 40, 1425-1442. https://doi.org/10.1109/18.333859